疲劳试验机举升架双缸同步控制研究

贾文昂,李展尚,陈统中,倪子帆,张善运

(1.浙江工业大学 机械工程学院,浙江 杭州 310023;2.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室,浙江 杭州 310023)

随着工业技术水平的提高,疲劳试验机作为测试材料力学性能和试件疲劳寿命极限的重要设备也得到越来越普遍的应用[1]。疲劳试验机主要由位置同步升降结构和高频激振器两部分构成,其在进行疲劳试验前需通过疲劳试验机举升架的同步升降来调节上夹头高度以适应长短不一的疲劳试验材料[2]。由于试件装夹装置与举升架是固连,而疲劳试验需要保证试件只受拉压,因此要求举升架双缸举升要同步,使举升架处于水平位置,以避免拉压分力的产生。控制策略是影响液压同步系统精度的主要因素之一,在同步控制策略环节,由于液压系统多参数、时变和非线性等特点,常规PID控制效果就不太理想。近年来,为解决PID控制器参数难以整定或控制性能不足的问题,学者们研究了多种整定方法和现代控制理论与PID相结合的复合控制方法,主要有遗传算法、粒子群算法和细菌群觅食优化算法等现代优化算法以及模糊控制、神经网络、人工免疫系统和自适应控制等控制理论[3]。

基于此,以疲劳试验机举升架双缸同步系统为研究对象,提出使用单神经元PID自适应算法克服传统PID算法在液压双缸同步中控制性能不足的难题,并对两种算法控制下的系统进行了对比仿真分析和试验研究。

1 同步系统理论基础

1.1 试验机举升架同步原理

试验机举升架同步原理如图1所示。由图1可知:疲劳试验机举升架同步系统主要由2个非对称液压缸、2个2D数字阀、2个MTS-磁致伸缩位移传感器以及控制器等关键模块组成。对系统输入位移控制信号后,控制器实时比较传感器采集的主动缸实时位置数据与输入参数,经过同步控制算法处理,输出控制信号给2D数字阀,通过控制2D数字阀来调整主动缸的油液流量以调节输出位移,同时主缸的位移值作为从缸的控制信号,以主从控制的方式达到两缸同步的效果。

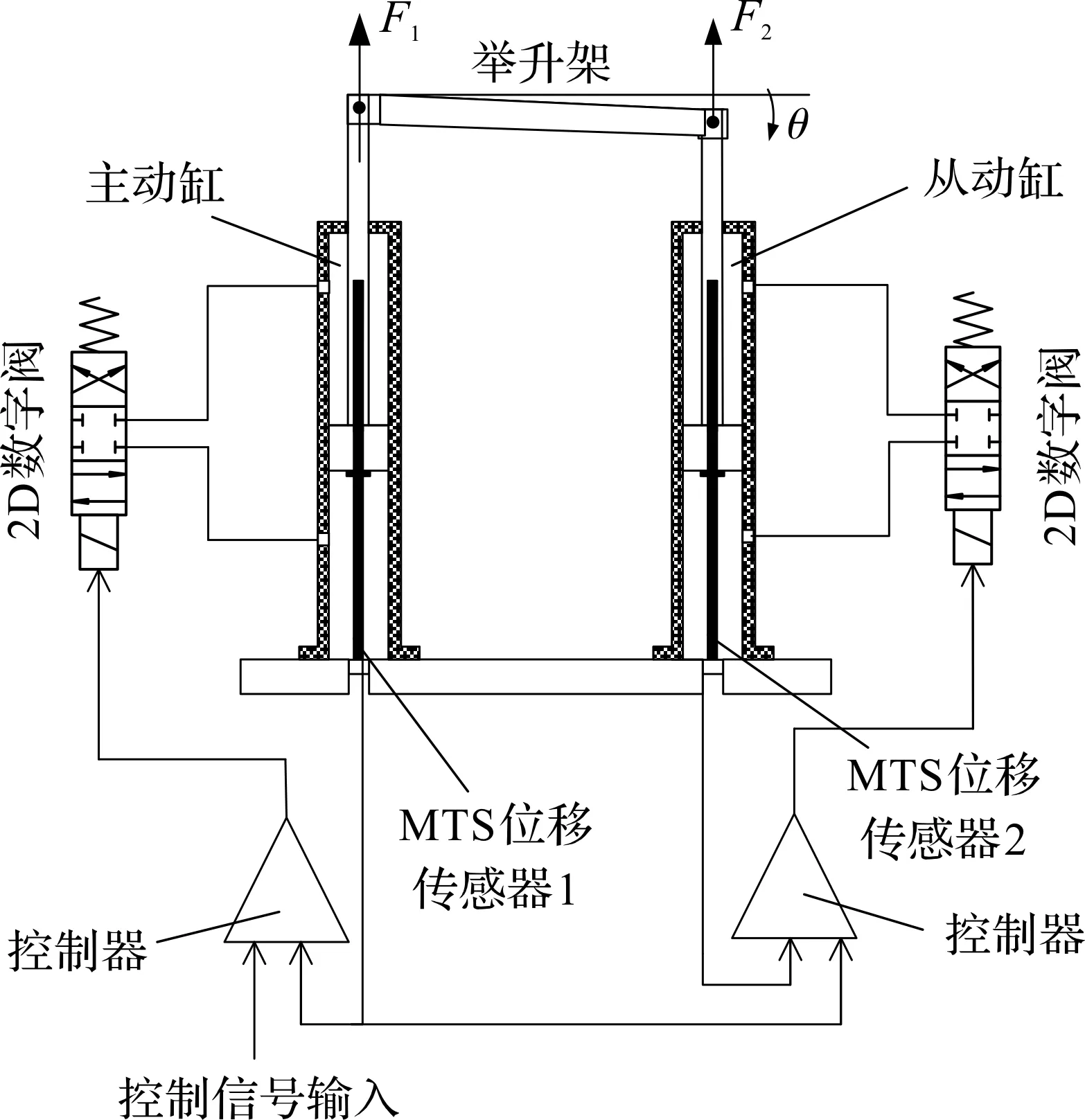
图1 试验机举升架同步原理图Fig.1 Synchronization schematic diagram oftesting machine

同步系统的控制元件采用笔者课题组研发的2D数字阀。相较于现有的其他伺服阀,其不仅具有无死区、无滞环和抗污染能力强等优点,而且液压固有频率高,响应速度快[4],在同步系统中应用2D数字阀可以克服磁滞、饱和等非线性影响,从而有效提高同步精度。

2D数字阀结构如图2所示。2D数字阀由阀体模块、步进电机和电机械转换器等部分组成,其步进电动机通过齿轮副和阀芯相连来控制阀芯的运动,当电机驱动控制器收到外部发出的信号时,开始控制电-机械转换器工作,将电信号转化转换为机械运动,带动阀芯做旋转运动,数字阀阀芯采用特有的螺旋伺服结构,阀芯旋转后,两腔的压力不再平衡,阀芯产生水平移动[5]。

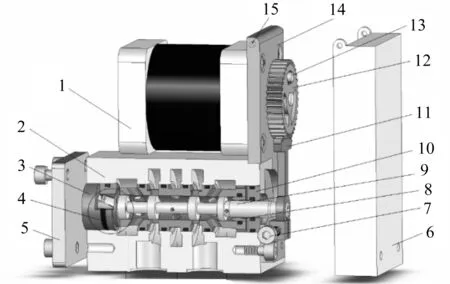
1—步进电动机;2—阀座;3—阀套;4—O形圈;5—挡板;6—盒盖;7—紧固螺钉;8—同心环;9—阀芯;10—端盖;11—摆轮;12—齿轮;13—限位销;14—电动机安装板;15—安装销。图2 2D数字阀Fig.2 2D digital valve

1.2 2D数字阀控液压缸建模

疲劳试验机举升架同步举升模块可以理解为两个一致2D数字阀控非对称液压缸系统[6]。2D数字阀控非对称液压缸的原理简图如图3所示。图3中:y表示活塞杆位移;FL表示外负载压力;A1表示无杆腔面积;P1表示无杆腔压力;V1表示液压缸进油腔容积;Q1表示无杆腔流量;A2表示有杆腔面积;P2表示有杆腔压力;V2表示液压缸回油腔容积;Q2表示有杆腔流量;Ps表示供油压力;P0表示回油压力;m表示活塞和负载总质量;βp表示活塞及负载的黏性阻尼系数;K表示负载弹簧刚度;xV表示2D阀芯轴向位移;Cip表示液压缸内泄漏系数;Cep表示液压缸外泄漏系数。

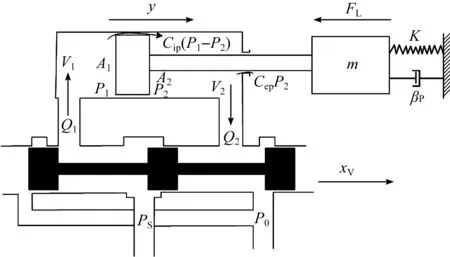
图3 2D数字阀控非对称液压缸原理简图Fig.3 2D digital valve controlled asymmetric hydrauliccylinder principle diagram

假定供油压力Ps恒定不变,回油压力P0=0,阀无泄漏,4个节流窗口匹配且对称,可建立2D数字阀线性流量方程式为

(1)

式中:Cd为流量系数;w为面积梯度;ρ为液体密度。

由式(1)可知

(2)

假定管道内的摩擦损失和流体质量影响忽略不计,液压缸油温和体积弹性模量为常数。建立流量连续方程式为

(3)

式中βe为等效弹性模量。

当xv>0时,定义负载压力和负载流量为

(4)

由式(1～4)推导出负载流量方程式为

(5)

式中:Cie为等效漏损系数,Cie=((1+n2)/(1+n3))Cip;Cia为附加漏损系数,Cia=((n2(1-n))/(1+n3))Cip;Vt为等效容积,Vt=2LA1/(1+n3),L为液压缸行程。

建立非对称液压缸力平衡方程式为

(6)

式中F为液压缸产生的驱动力。

式(1,3,6)确定了2D数字阀控缸的动态性能,对式(1)进行线性化处理后得

(7)

式中:kq为阀的流量增益;kc为阀的流量—压力系数。

对式(5～7)进行拉氏变换后,整理可得阀芯位移输入xv与外负载FL同时作用下的液压缸活塞位移输出模型为

(8)

式中:Kta为总流量压力系数,Kta=kc+Cie;Qea为附加漏损流量,Qea=Cia+Ps。

在2D阀控缸系统中将弹性负载忽略不计,取K=0;黏性阻尼系数βp非常小,即βpKta/A12≪1。式(8)可以简化为

(9)

(10)

式中:wh为液压固有频率;ζh为液压阻尼比。

(11)

当xv<0时,定义负载压力和负载流量分别为

(12)

同理可推得

(13)

根据文献[7],2D数字阀螺旋机构的传递函数为

绿色GDP的理论和技术是实施绿色GDP的重要条件，因此，必须要不断加强绿色GDP的理论和技术研究，保证绿色GDP的实施。

(14)

其中

(15)

(16)

(17)

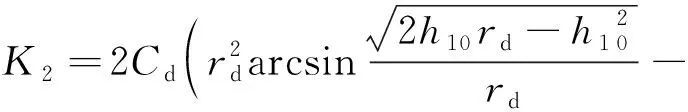
(18)

式中:ms为折合到阀芯总质量;β为螺旋槽升角;Lv为数字阀左敏感腔初始长度;rd为高(低)压小孔半径;h10为平衡点的弓形高度;A为左腔的阀芯面积。

电机械转换是将电信号转换成电机转子的旋转运动,其作用效果是一种线性模型,简化成一个比例环节为

(19)

式中:Ka为增益;θ为电机转子角位移;U为输入电压。

选用的位移传感器可以简化为一个比例环节,即

(20)

式中:Uf为位移传感器反馈输出电压;Y为液压缸活塞位移;Kf为位移传感器灵敏度系数。

根据式(9～20),可以建立2D数字阀控非对称缸的数学模型,系统框图如图4所示。由图4可知:输入的控制信号为电信号,2D数字阀的电机械转换器将电信号转换成阀芯位移以控制输入液压缸的流量,同时位移传感器将输出的位移值转换成电信号反馈到输入环节,形成闭环系统。

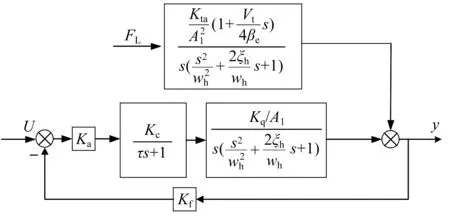
图4 2D数字阀控非对称液压缸系统框图Fig.4 Block diagram of 2D digital valve-controlledasymmetric hydraulic cylinder system

2 控制策略

单神经元的基本结构[8]如图5所示。

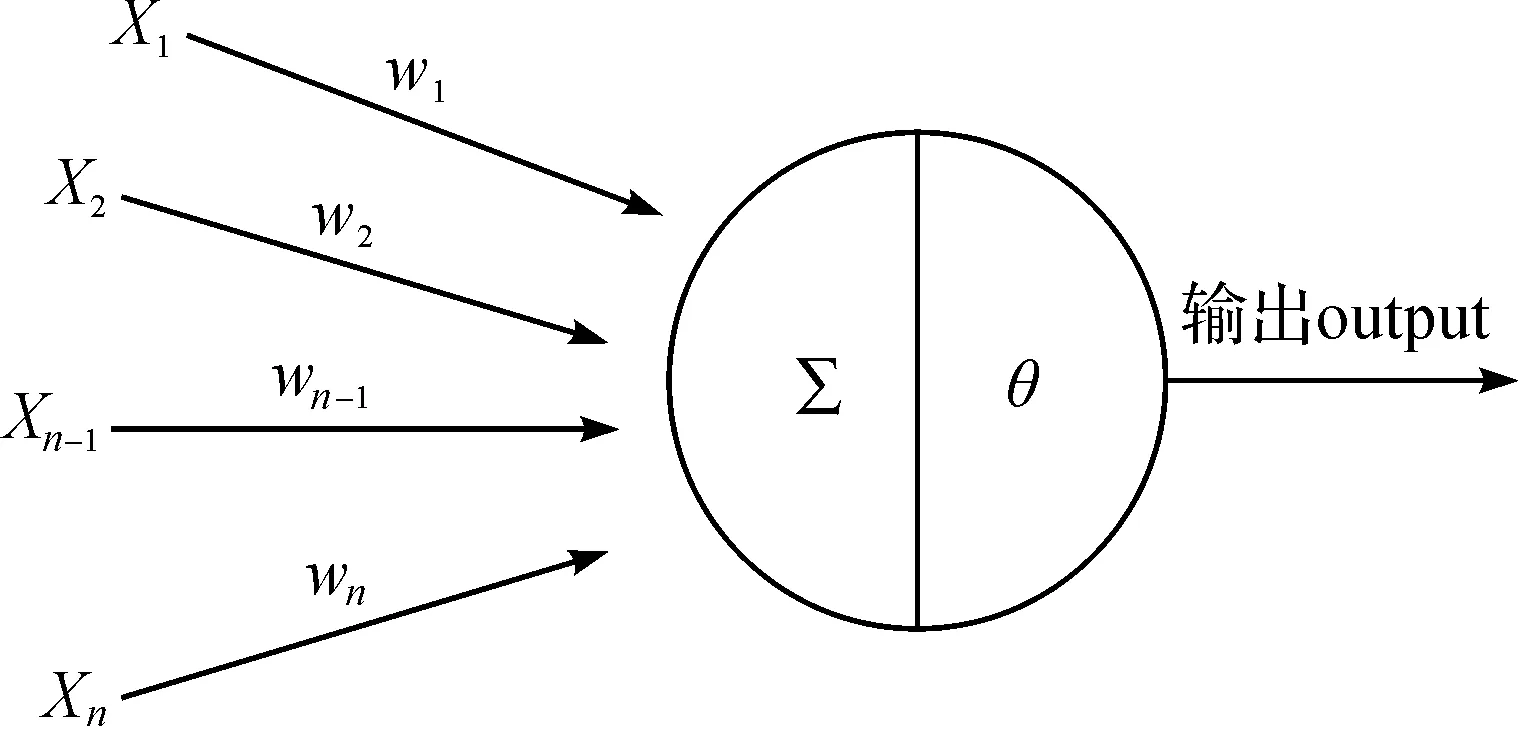
图5 单神经元结构模型Fig.5 Single neuron structure model

(21)

式中θ为阈值。

利用单神经元模型对普通PID控制进行改进,可以得到单神经元PID自适应控制框图,具体如图6所示。

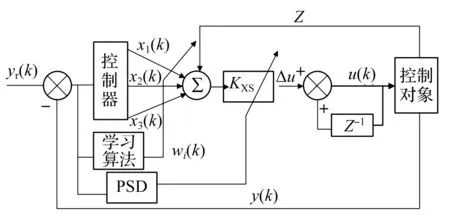
图6 单神经元PID自适应框图Fig.6 Block diagram of single neuron adaptive

图6中控制器输出的x1(k),x2(k),x3(k)分别对应传统PID控制的比例、积分、微分;权值w1,w2,w3分别对应比例系数、积分系数、微分系数;yr(k)为参考输入值;y(k)为实际输出值;u(k)为神经元的输出信号。神经元所需的输入量由控制器输出为

(22)

式中:u(k-1)为前一时刻控制器的输出;Kxs为神经元的比例系数;xi(k)为单神经元学习所需的状态量;wi(k)为对应各个状态量的加权系数,表达式为

(23)

单神经元PID自适应的增益系数Kxs值直接影响整个神经元系统的性能,对于未知开环增益的系统,如果Kxs值可以随开环增益而改变,将有利于提升整个系统的鲁棒性。使用PSD算法对Kxs值进行调整[9-10],计算式为

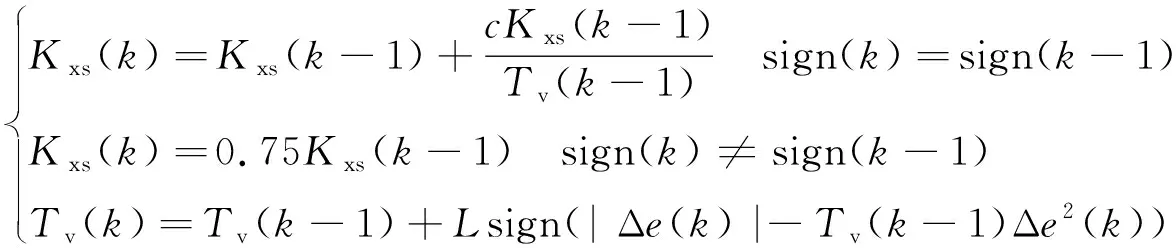
(24)

式中:0.025≤c≤0.05;0.05≤L≤0.1;Kxs>0。

图6的学习算法使用有监督的Hebb算法作为单神经元的学习规则,具体学习规则为

wj(k)=η(dj(k)-oj(k))oj(k)oi(k)

(25)

式中:η为学习速率;dj(k)为期望输出;oj(k)为神经元j的激活值;oi(k)为神经元i的激活值。

单神经元控制主要通过对加权系数的调整来实现自适应功能,考虑到有监督的Hebb学习算法在实际应用中经常出现控制增量过大的情况,在设计控制策略中采用输出误差和控制增量的加权平方来优化加权系数[12]。设指标为

(26)

式中:P为输出误差加权系数;Q为控制增量加权系数;d为滞后。

当主缸与从缸的误差减小,性能指标E(k)也要随之减小,即加权系数wi(k)要向算法函数的负梯度方向进行搜索,加权系数wi(k)的调整量[13]为

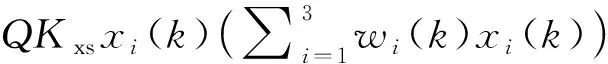
(27)

式中:ηi为算法学习效率;b0为输出响应的最小值。

根据式(21～27)建立单神经元PID自适应控制器,整体系统框图如图7所示。通过单神经元PID自适应控制器跟踪一个参考输入量r1,根据液压缸的实际输出值y1自行学习2D数字阀的控制函数,进而对比例系数Kxs和权值进行自适应调整,以克服整个液压系统中的非线性因素。

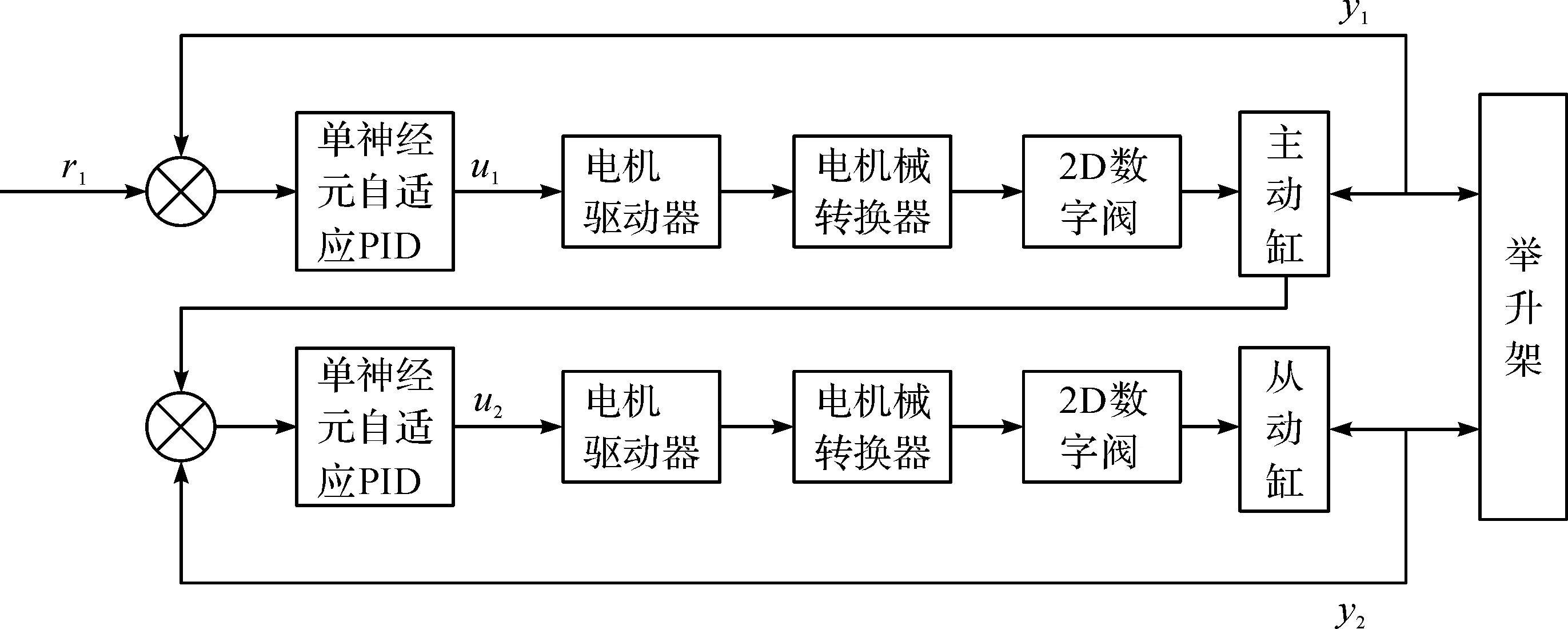
图7 单神经元PID自适应控制下的系统框图Fig.7 Block diagram of single neuron PID adaptive control system

3 仿真研究

使用Matlab/Simulink仿真模块,根据建立的2D数字阀控缸数学模型以及单神经元PID自适应算法搭建仿真模型,该模型参数如表1所示。

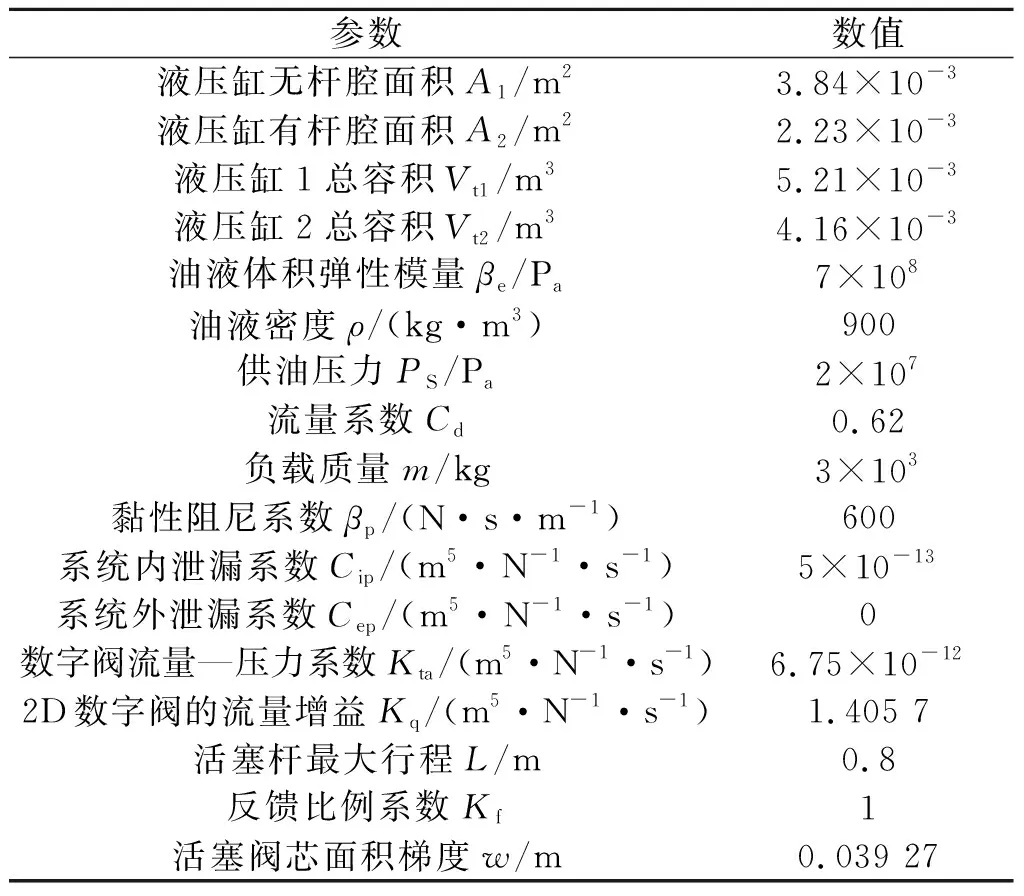
表1 仿真参数表Table 1 Simulation parameter table

搭建传统PID控制的仿真模型如图8所示。由图8可知:输入为80 mm的阶跃信号,设置主缸PID控制最优参数Kp=0.012,Ki=0.005,Kd=0,从动缸PID控制最优参数Kp=0.035,Ki=0,Kd=0。输入信号经过PID模块输入2D数字阀的控制函数,在外负载的作用下最后得到双缸同步运动曲线和位移偏差曲线。PID控制下双缸同步曲线如图9所示。由图9可知:受主从控制方式的影响,系统启动时从动缸的移动会滞后于主动缸的移动,启动初同步系统的偏差理论会达到最大值。同步系统在PID控制下主动缸和从动缸的位置偏差曲线如图10所示。由图10可知:在PID控制选取最优参数的情况下,系统最大偏差为2.72 mm,以两缸位置偏差值可以判断整个双缸同步系统稳定时间约为25 s,整个同步系统在PID控制下,最后的两缸位置静态误差为0.077 mm。单神经元PID自适应控制下的同步系统仿真模型如图11所示。由图11可知:输入信号为80 mm的阶跃信号,设置两缸的w1,w2,w3初始值为0.1,主动缸最优K值为0.58,从动缸最优K值为0.71,主动缸的PID控制3个参数的学习速率分别设定为12,0.5,0,从动缸的PID控制3个参数的学习速率分别设定为15,1.2,0。

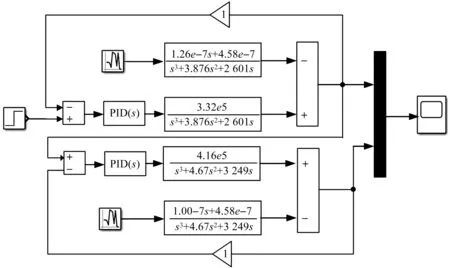
图8 PID控制的仿真模块图Fig.8 Simulation module diagram of PID control

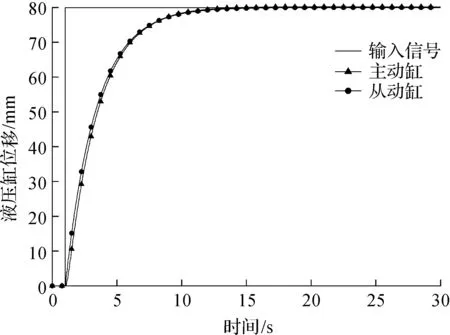
图9 PID控制下双缸同步曲线图Fig.9 Synchronization curve of two cylindersunder PID control

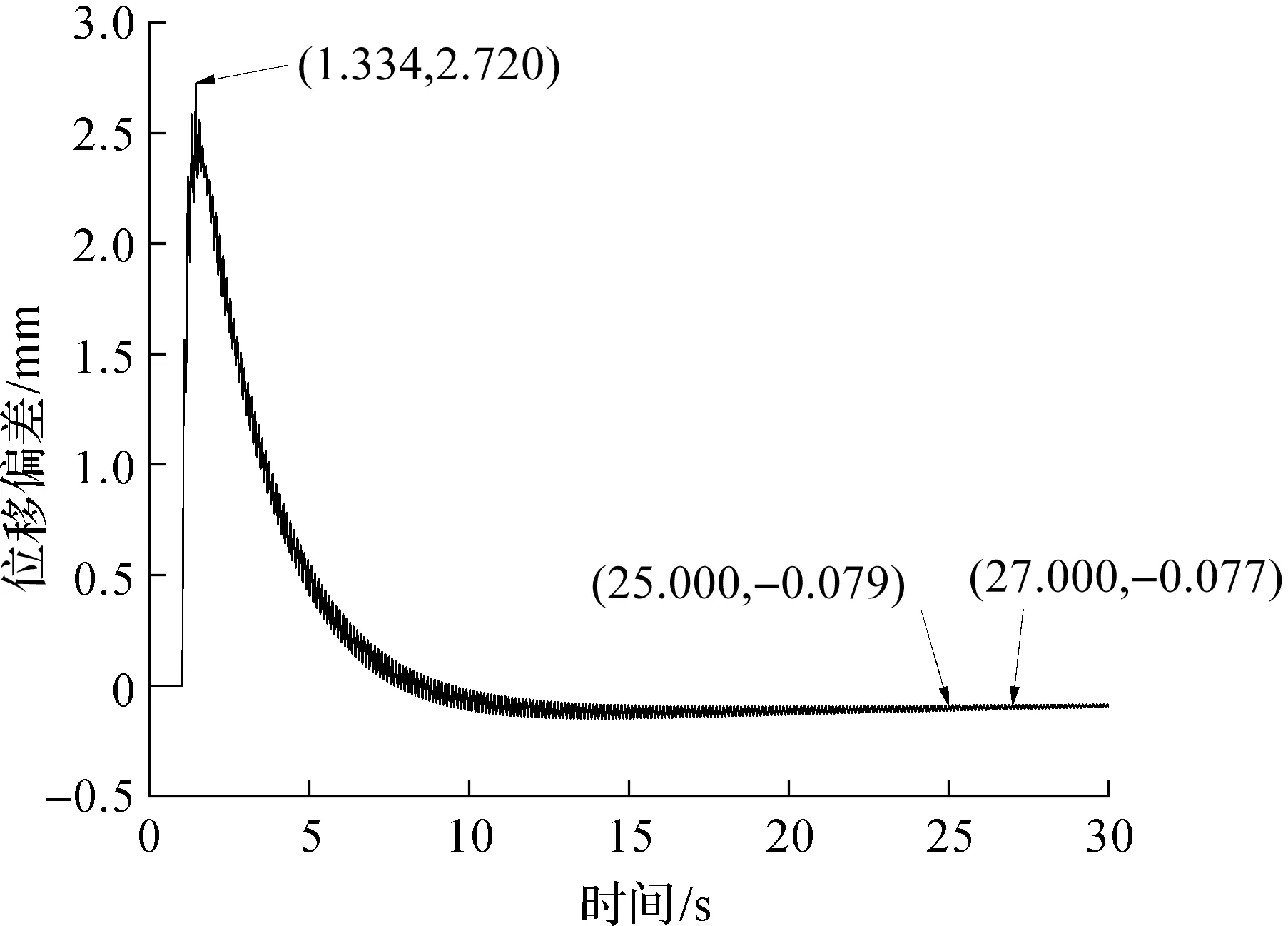
图10 PID算法控制下双缸同步偏差图Fig.10 Synchronization deviation diagram of twocylinders under PID control

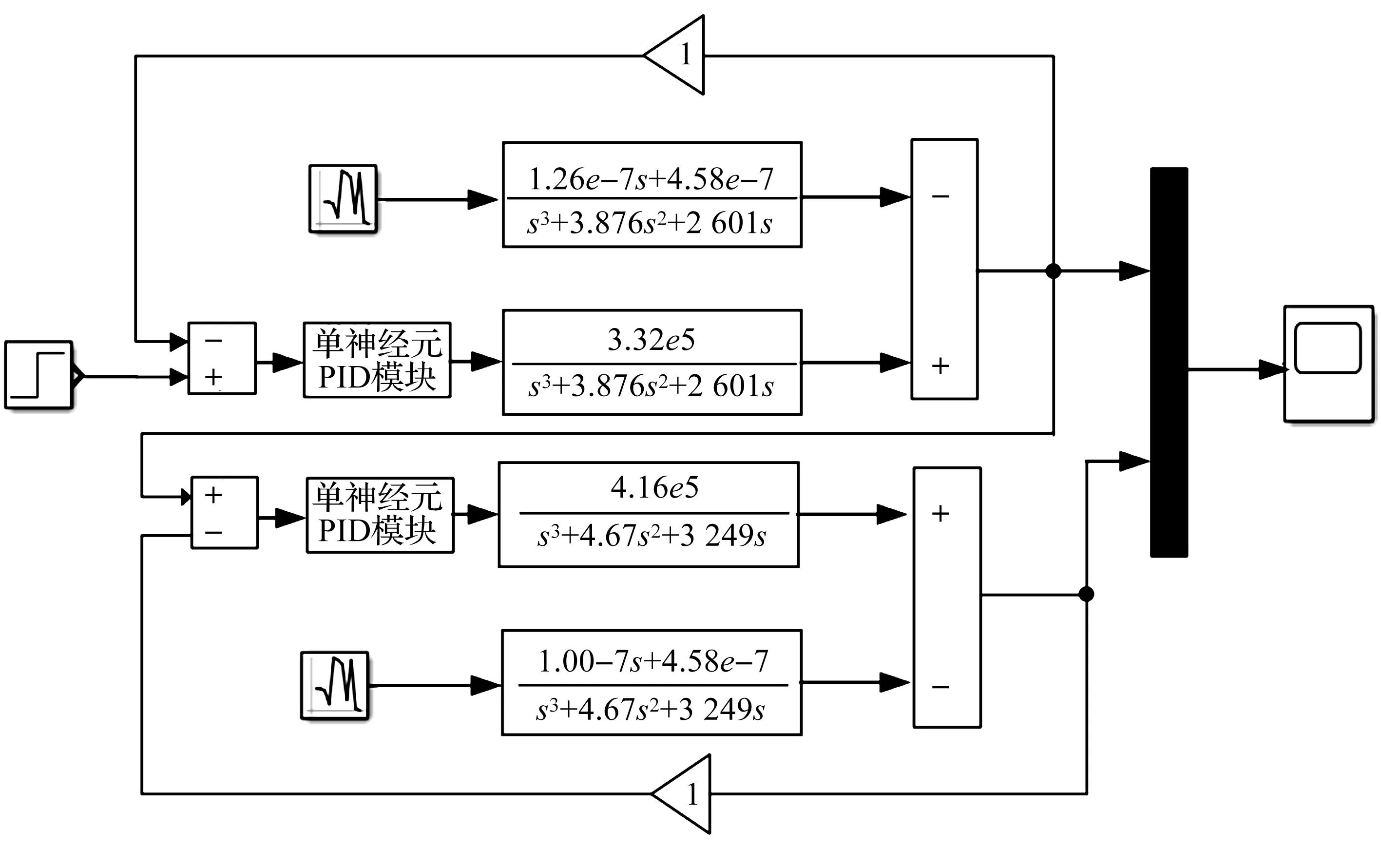
图11 单神经元PID自适应控制仿真图Fig.11 Simulation diagram of single neuron adaptive PID control

仿真得到单神经元PID自适应控制策略下主从两缸的位置曲线和位置偏差曲线分别如图12,13所示。由图12,13可知:整个双缸同步系统在启动状态下最大偏差为0.981 mm,从系统偏差曲线可以判断整个同步系统在单神经元PID自适应算法控制下,稳定时间约为15 s,稳态误差几乎为0 mm。

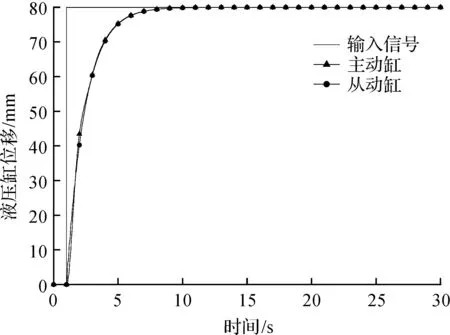
图12 单神经元PID自适应控制下双缸同步曲线图Fig.12 Synchronization curve of two cylinders under singleneuron adaptive PID control

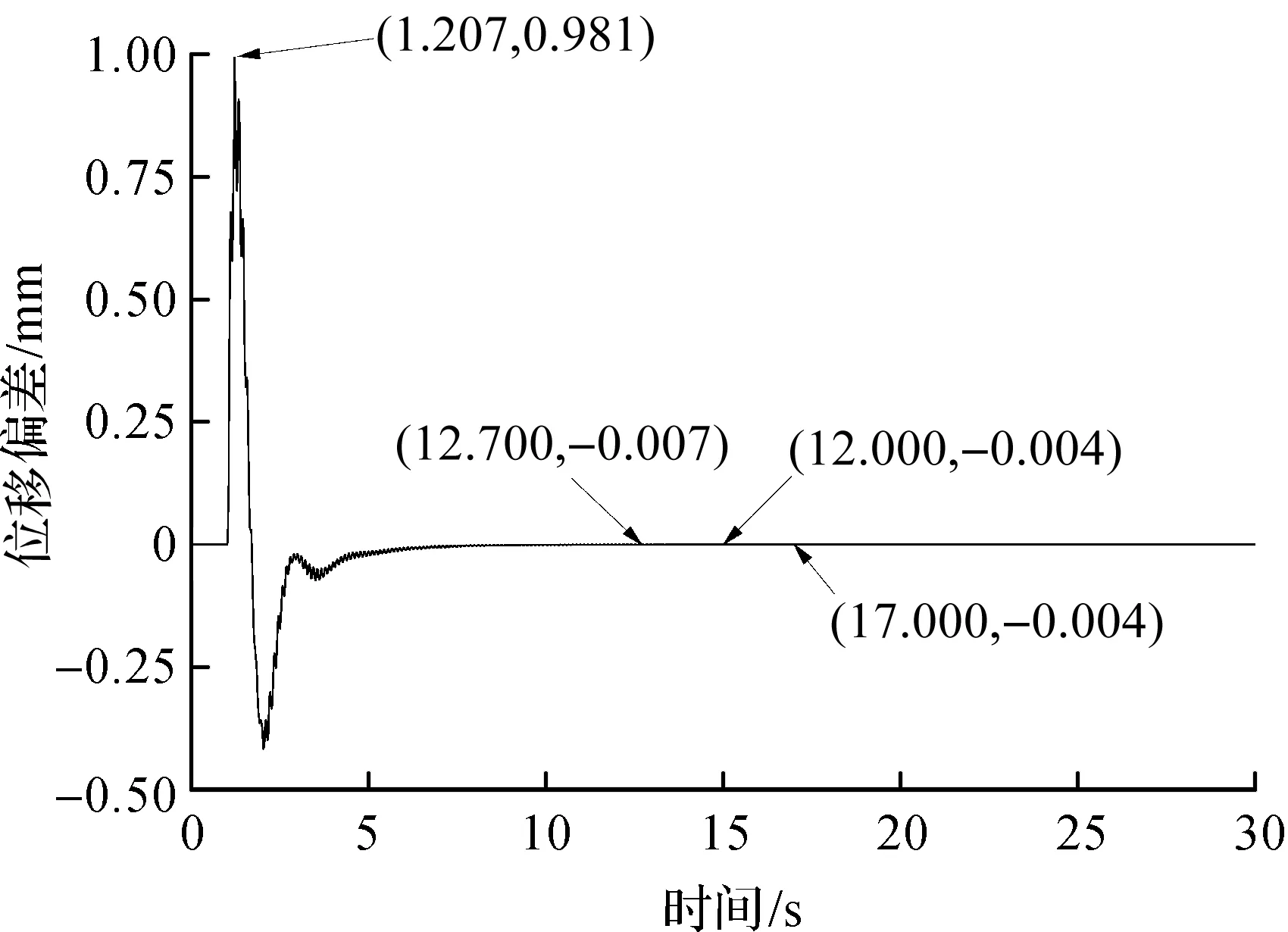
图13 单神经元PID自适应算法控制下双缸同步偏差图Fig.13 Synchronization deviation diagram of twocylinders under the control of singleneuron PID adaptive algorithm

与传统PID控制下的双缸同步系统仿真结果相比:1) 运用单神经元PID自适应控制策略,可以有效降低整个同步系统运行中主从两缸的位置偏差,传统PID控制的同步系统主从两缸最大位置偏差为2.72 mm,应用单神经元PID自适应控制策略后,主从两缸最大偏差降低至0.98 mm;2) 运用单神经元PID自适应控制策略,可以提升整个系统的响应速度,传统PID控制的同步系统达到稳定的时间为25 s,应用单神经元PID自适应控制策略后,整个同步系统达到稳定的时间为15 s,系统达到稳定的速度得到明显提升;3) 单神经元PID自适应控制下的同步系统静态误差比传统PID控制的同步系统更小。由图13仿真结果可以看出:同步系统稳定后,主从两缸的实际位置与控制信号一致。因此,运用单神经元PID自适应控制策略可以有效提高双缸同步系统的同步精度和响应速度。

4 试 验

4.1 试验设备

试验在实验室自主研发的2 500 Hz疲劳试验机设备上完成,2 500 Hz疲劳试验机结构如图14所示。同步系统的执行设备主要包括举升架、主动缸、从动缸、2D数字阀和位移传感器。

图14 2 500 Hz疲劳试验机Fig.14 2 500 Hz fatigue testing machine equipment

同步系统的控制器如图15所示。

1—24 V开关电源;2—信号接口转接模块;3—散热模块;4—电源模块;5—2D数字阀驱动控制模块;6—双缸同步控制模块。图15 同步系统控制器Fig.15 Synchronous system controller

4.2 同步举升试验

在疲劳试验机上分别进行两种控制策略下的同步举升试验。传统PID控制策略下的举升架同步试验曲线如图16所示。由图16可知:从动缸的运动在系统启动初滞后于主动缸,在10 s后从动缸的实际位置超前于主动缸实际位置,从动缸跟随主动缸的运动效果不佳。

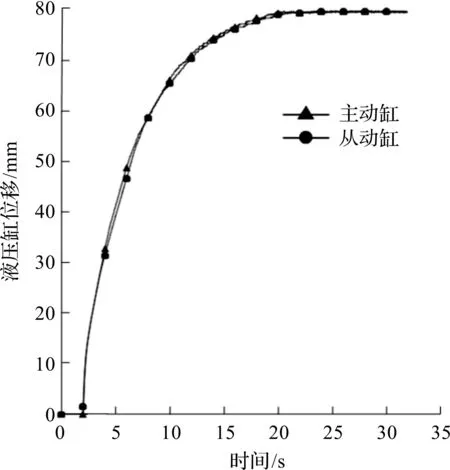
图16 PID控制下双缸同步位移试验曲线图Fig.16 Test diagram of double cylinder synchronousdisplacement curve under PID control

单神经元PID自适应控制策略下的举升架同步试验曲线如图17所示。由图17可知:在整个运动过程中,从动缸跟随主动缸的运动没有出现超前的情况。

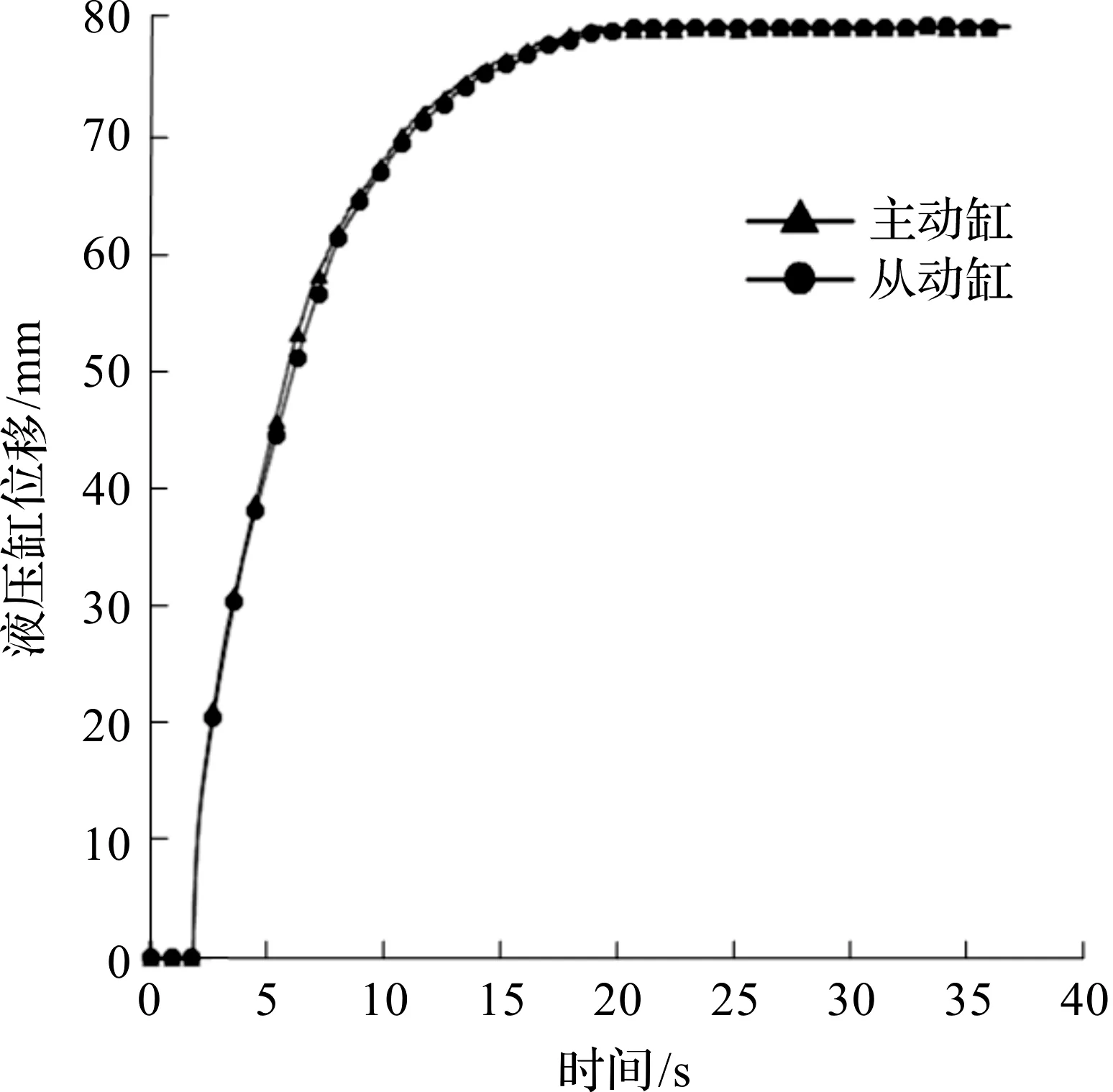
图17 单神经元PID自适应控制下双缸同步位移试验曲线图Fig.17 Synchronous displacement test curve of double cylinderunder single neuron adaptive PID

PID控制和单神经元PID自适应控制策略下的同步试验偏差曲线图分别如图18,19所示。由图18,19可知:PID控制主从两缸最大偏差接近3 mm;单神经元PID自适应控制策略下主从两缸最大偏差为1.2 mm。

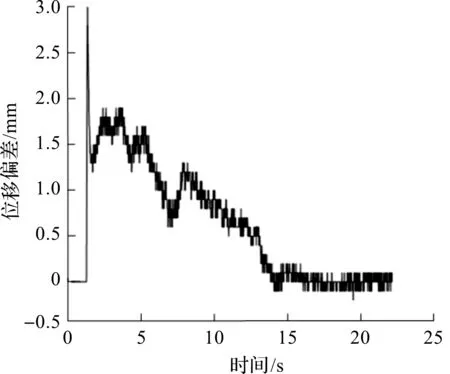
图18 PID控制下双缸同步试验偏差图Fig.18 Deviation diagram of double cylinder synchronoustest under PID control

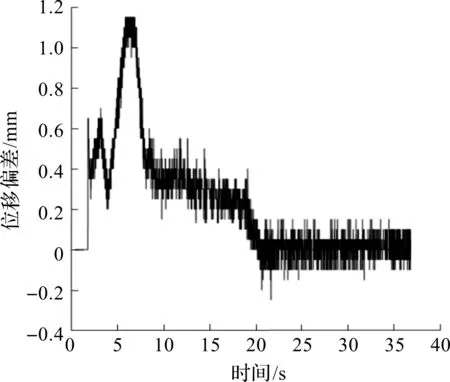
图19 单神经元PID自适应控制下双缸同步试验偏差图Fig.19 Deviation diagram of double cylinder synchronous testunder single neuron adaptive PID control

由试验和仿真结果可知:应用单神经元PID自适应控制策略,仿真上整个同步系统的最大偏差为0.98 mm,静态误差约为0 mm;试验上整个同步系统的最大偏差为1.2 mm,静态误差约为0.15 mm。应用PID控制策略,仿真上整个同步系统的最大偏差为2.72 mm,静态误差约为0.07 mm;试验上整个同步系统的最大偏差为3 mm,静态误差为0.3 mm。两种控制策略的试验结果与仿真结果虽然存在误差,但在趋势上保持一致,仿真结果相较于试验结果抖动小,系统稳定速度更快,同步相对误差小,主要原因是在试验过程中,一方面液压系统存在仿真模型无法还原的非线性因素;另一方面实际同步控制器的响应时间达不到仿真模型设定的响应时间。但总体来看,整体试验的误差在合理范围之内,试验和仿真的结果较好地验证了设计的单神经元PID自适应控制策略在双缸同步系统中的控制效果优于传统PID控制策略,整个同步系统的同步精度得到有效提升。

5 结 论

通过分析疲劳试验机举升架双缸同步的工作原理,推导建立了同步控制系统模型。使用单神经元PID自适应算法作为同步系统的控制算法。通过仿真和试验,分别对比了使用常规PID控制算法和单神经元PID自适应算法作用下的疲劳试验机主从液压缸的同步误差。仿真结果表明:单神经元PID自适应算法下同步系统的同步误差率为1.23%,传统PID控制下同步系统的同步误差率为3.4%,单神经元PID自适应在同步精度方面明显优于传统PID控制。试验结果表明:单神经元PID自适应算法下同步系统实际的同步误差率为1.5%,传统PID控制下同步系统实际的同步误差率为3.75%,试验与仿真结果存在较小误差,证明了应用单神经元PID自适应算法可以有效提高液压双缸同步系统的同步性能。