小学数学建模怎样进行——“商的变化规律”教学赏析

浙江台州市仙居县步路乡中心小学（317305） 张敏

什么是数学建模？教师该如何帮助学生进行数学建模？在观摩了吴正宪老师的一节示范课后，笔者茅塞顿开。吴老师的授课内容是人教版教材第七册“商的变化规律”。对于这样的常规课，吴老师还能“玩”出什么新花样呢？

上课伊始，吴老师并没有什么神来之笔，她以“猴王分桃”的故事指引学生列出三个对应的除法算式“6÷2=3、60÷20=3、600÷200=3”，并依次进行辨析。这一方式让我们的期望落空，情绪有些失落。突然，吴老师来了个180度大转弯，犹如惊雷炸响，让我们眼前一亮。

一、借助几何直观，勾勒模型轮廓

待学生初步认识“猴王分桃”的三个算式后，吴老师没有让学生对三个算式蕴含的规律进行继续挖掘，而是以几何直观的形式来揭示规律。

师：这三个算式蕴含着什么规律？我们慢慢揭晓。再来看一组题。（题目省略）

师（出示图1）：从图中你能发掘出哪些数学信息？

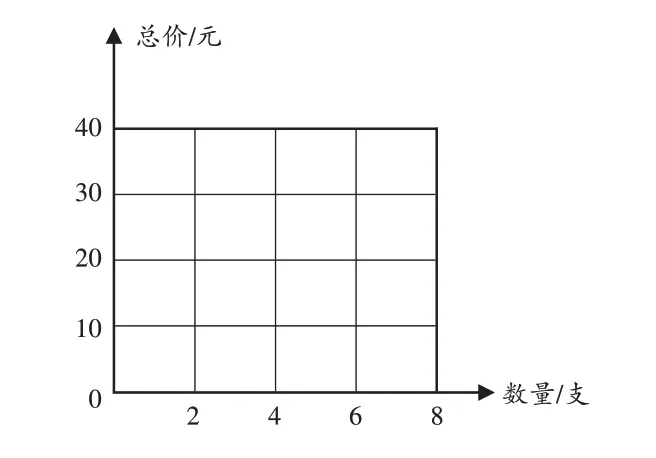
图1

生1：横轴坐标表示短笛的支数，纵轴坐标表示相应的总价格。

师：你知道两者之间存在什么数量关系吗？

生2：采购2支短笛需支出10元，采购4支短笛需支出20元，采购6支短笛需支出30元，采购8支短笛需支出40元。

（学生边说，教师边在图中描点，得到图2）

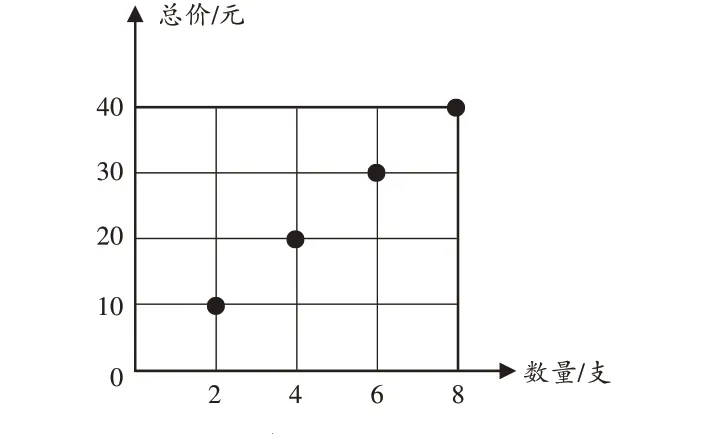
图2

师：想一想，采购10支短笛时，横纵轴的交汇点会跑到哪儿？

生3：延长横轴末端，往上就可以找到它。

师：你发现了什么新线索？

生4：每个点的纵坐标数除以横坐标数，得到的商都是5。

师：这个商5有什么实际意义？

生5：它表示一支短笛的单价。

师：你是从何得知的？

生6：用采购短笛的总价格除以短笛的支数，可得一支短笛的单价。

师：短笛的数量和总价一直不固定呀。

生7：但是无论数量和总价格如何变化，一支短笛的单价5元一直不变。

（此时，吴老师没有满足于学生对坐标图的观察和理解）

师：你们的意思是，随着采购的短笛的支数不断增多，需要支付的钱款也会增多，但是每支短笛的单价一直不变。

（吴老师边说边伸直左右手，左手平伸代表横轴，右手竖直代表纵轴，两条手臂慢慢伸展，使学生从肢体动作中体验到被除数和除数同步增加的过程，揣摩商不变的本质。）

传统的建模都是先出示一个情境，然后在大量类似的情境和变式中归纳出运算公式，最典型的是植树问题模型，其先出示大量的植树问题，让学生从中概括出植树问题的模型，那就是“间隔数+1=棵数”，然后通过变式继续扩大、丰富模型，概括出“间隔数-1=棵数”“间隔数=棵数”两个种子模型。即使是“比例”这种模型，一般也是从相关变量中进行概括构建（如速度一定，路程与行驶时间成正比），并利用表格来展示和总结。这样的建模缺少直观性，而且学生很难建立变量的连续变化思想（也就是函数思想）。吴老师的这种建模独树一帜、别开生面，直接跳过对直观表象的提炼，出示平面坐标系，用坐标系中的函数图像来直观揭示两个变量的变化关系，这比直接出示短笛的图片和相应价格要高明得多。这种数学模型具有高度的概括性和抽象性，且因具有几何直观而更具说服力。

二、分层渐进感悟，初步建立模型

在上述建模的基础上，吴老师指点学生重新探寻算式的变化规律。

师：这些算式的商为何始终固定为一个值？请大家任选一个题组，把自己的发现如实记录下来。

（学生小组合作探究）师：谁来展示一下自己的探究历程和研究成果？学生展示自己的探究历程和研究成果，如图3：

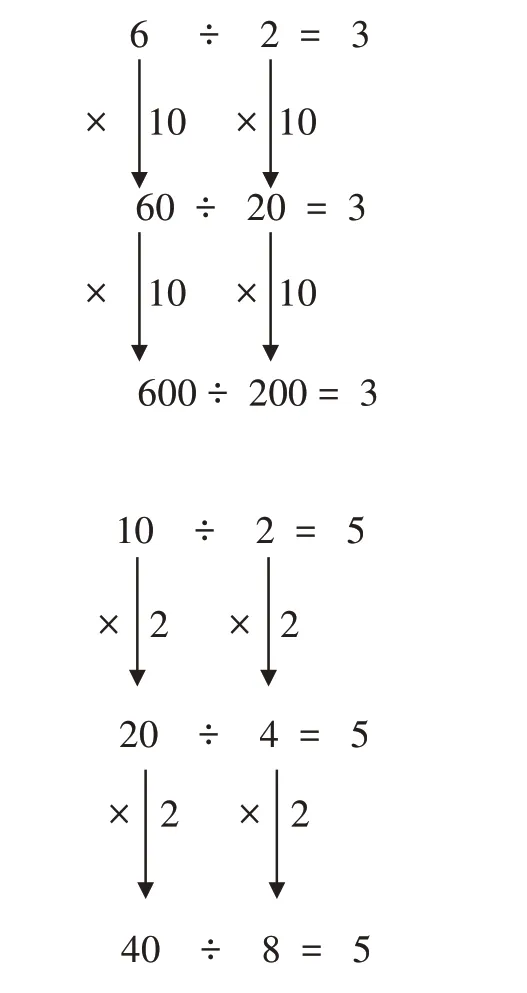
图3

师：你能根据探寻出的规律，写出几组算式吗？

生1：4÷2=2，40÷20=2……

生2：8÷2=4，80÷20=4……

生3：20÷5=4，200÷50=4……

师：你们说得完吗？

生4：无穷无尽，数都数不清，终其一生也休想说完。

师：那么如何用一句话或者一个式子来高度概括无法说尽的道理和规律呢？你想到什么，就直说，一时说不清就整理成文后再交流。

（学生反思整个学习过程，将自己的心得体会整理成文）

生5：商的大小与被除数、除数之间的比例有某种潜在的关系。

师：你们想从他嘴里再问出点什么吗？

生（齐）：这种潜在的关系到底是什么？

生5：比如被除数乘2，除数也乘2，那么商就始终为一个定值。

生6：被除数乘10，除数乘10，商也会为一个定值。

生7：被除数乘几，除数也乘几，商会为一个定值。

师：换言之，谁和谁同时乘同一个数，商才会为一个定值呢？

生8：被除数和除数同时乘同一个数，商会为一个定值。

师：很好，这位同学做了高度凝练的概括。你们还有要补充的吗？

生9：在总结的时候，要一次性考虑到所有情况，不能有一个例外。

师：对的，要把所有情况全部囊括进去。

师（出示图4）：有的同学是这样归纳的，你对此有什么看法？

图4

生10：我觉得把方框替换成字母x更贴切。

师：x表示什么？

生11：任意数。

在这个环节中，吴老师引导学生说出心中所想，学生的想法在吴老师的问题下不断成熟和完善，由最初的“无穷无尽”到“被除数和除数同时乘几，商就不会变”，再到用字母x这个简约的符号来代替方框。这不仅体现了学生由浅薄到深厚的积累积淀过程，也展现了由学生形象感知到理性分析和抽象概括的思维过程，更重要的是，他们尝到了建模的滋味，体会了数学建模的意义。诚然，有了充分的体验、渐入佳境的感知，学生的总结才能够直击要害“要把所有情况囊括进去”，这个“把所有情况囊括进去”的符号表达就是一个数学建模的过程。

虽然前期建立了一个函数模型，但只是揭示正比例关系，而非本课的核心主旨。本课的核心是商不变规律，前期的模型只是一个框架、一次预演，让学生发现商（总价与数量的比）不变时，两个变量存在某种特殊关系，而这种特殊关系要确认无误地表述出来，才能完成对商不变规律模型的构建。吴老师先顺接前一个模型反映的数据特征，提取出算式，让学生观察几组商不变的除法算式的特征，接着将算式对称排列，用箭头指出被除数和除数相同的变化规律，最后让学生应用规律创造算式，发现“无穷无尽”。在教师的引领下，学生对原有规律不断完善和抽象，最后成功总结出商不变规律：被除数和除数同时扩大或者缩小相同倍数，商不变。

三、回首全程，投用模型于实践

假如说前面的学习只是学生在顺着教师制定的路线走，只是在教师授意和监督下进行的抽象概括，那么怎样让学生在后续的学习中摆脱教师的牵引，自己发现新规律，并且能试着用抽象简约的符号来记录这种规律，是这节课的一个重要战略调整，也是教学理念的一次升华。于是吴老师组织学生再次回望学习全过程。

师：回望我们探究的过程，这个规律到底是怎样出炉的？

电子白板呈现画面和过程：猴王分桃→采购短笛账目的坐标图→自己看图写算式→检验真伪。

师：看这个坐标图（如图5），如果抹去计量单位“元”和“支”的话，你能编一个小故事吗？

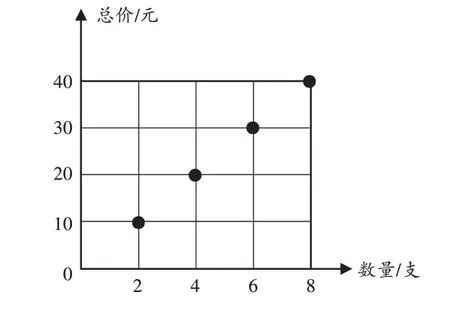
图5

生1：我购买2块橡皮泥用了10元钱，购买4块橡皮泥用了20元钱……每块橡皮泥5元钱。

生2：我练字，2分钟写了10行字，4分钟写了20行字……每分钟写5行字。

……

如果说前面的建模，是一种筹建和搭建，那么此环节就是在应用模型，属于模型投用阶段。让人惊喜的是，吴老师的模型投用，再次和几何直观勾连上了。

综观吴老师的授课过程，不难发现，她坚决贯彻建模思想。为了构建出“商不变规律”这个目标模型，前期建立了两个小模型作为基础和框架，当目标模型建立完毕后，前期建立的“框架”还可以循环利用，应用到别的情境中。对模型的应用绝不仅仅是将这个模型中蕴含的公式拿来解题，而是运用这个模型的基本框架去“度量”各种不同的情境，让同一模型在不同的情境中发挥价值，利用这一模型去对照、整合不同情境下的数量关系，发现不同情境下存在共同数量关系的可能，即从不同路径去验证这个模型的可靠性和稳定性。简言之，模型可以用来“度量”不同的情境，不同的情境又可以检验模型的科学性。

综上，建立数学模型的过程需要学生在分层感知中逐步地完善和抽象，是学生对体验的不断沉淀和丰盈。对此，教师要多等待，少说教，少灌输。只有这样，“建模课堂”才会惊喜不断，精彩纷呈。