组合图形面积计算中的错例回收与利用

江苏苏州市吴中区胥江实验小学（215164） 郑介良

学生的错误本身没有价值，师生从错误中汲取的经验教训才是其价值所在。在新授课之前，教师要预估学生可能犯下的错误，及早采取预防措施，尽量减少错误的发生率；调整策略，让学生的错误全部曝光，并让学生正视自己的错误，认真反省，汲取教训。

一、课前错例分析

在学校举办的教研活动中，笔者教学的是“组合图形的面积”。组合图形的面积是一个教学难点，但课时又相对少。教材的编排是先让学生认识组合图形，再通过例4（墙面面积的计算）引导学生将组合图形分解成基本图形，然后展示两种算法（两种算法均为裁剪法，添补法出现在练习中），借此传递算法多样性和算法的优化。

如果教学目标仅仅是将组合图形切割或者添补成一个规则图形，就浅薄和短视了。因为求组合图形的面积有很多方法，不能让学生拘泥于一种模式，要为学生精心准备素材，体现多样的分割方法，思维训练要有序展开、分层推进，以激活学生的想象力和创造力，让学生清楚地意识到，分割也是有讲究、有分寸的，要根据题干条件合理分割，分割的原则是最后需要单独计算面积的区块最少。

例如，求图1的图形面积。

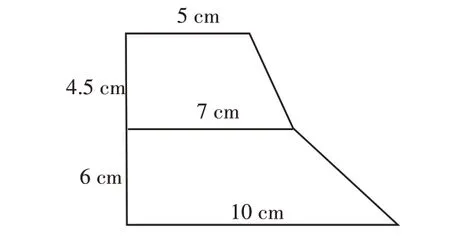
图1

【错解】（5+10）×（4.5+6）÷2=78.75（cm²）。

【原因分析】学生简单地将两个梯形合并成一个梯形，遗漏了中间的“公共底边”，其实两个梯形的斜腰并不在一条直线上。造成这种错觉是情有可原的，因为很多学生只关心上底、下底和高，而忽视梯形的斜腰。例如，图2也会被学生误认为是梯形，于是（2+7）×5÷2=22.5（cm²）这样的错误算式就出现了。对此，教师应该注意培养学生对组合图形的观察能力，通过眼力将其准确完美地“分割”到位。

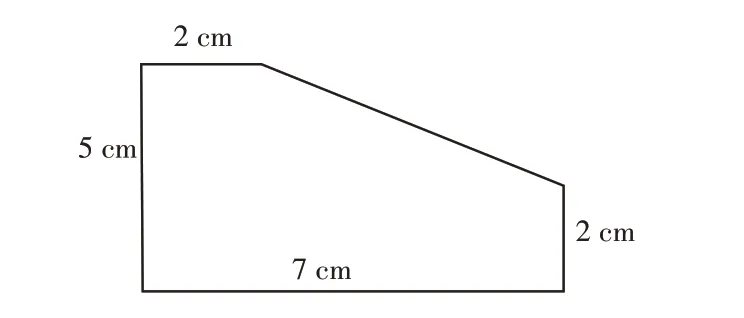
图2

图1中的两个梯形组合所得不是一个新的梯形，但学生却在寻找捷径的心理暗示下，以为其组合成了新的规则图形（大梯形），想利用公式一次性搞定，结果却是走了冤枉路。教师如果教学时一味强调图形面积求法的技巧性和灵活性，就会造成这样的结果。因此，教师教学时不能急功近利，要引导学生从基础的分析入手——先判断组合图形是否具备可转化性。

二、教学前测与预设

在教学“组合图形的面积”前，笔者对学生做了一次前测。

1.预习目标：（1）能自述什么是组合图形；（2）初步谈谈怎么求组合图形的面积。

2.自学指导：

（1）课本第92、93页提供的组合图形有何独特之处，又有哪些一般组合图形的共性？我认为组合图形是_________________。

（2）尝试解答课本第93页的“练一练”中的习题，不会的做上记号。

（3）计算组合图形的面积时有何细节？你还有其他问题吗？

前测结果显示，对于“什么是组合图形”这一问题，由于生活中的实例较多，所以学生回答起来没什么难度；对于“计算面积时的细节”和“还有什么问题”，47.6%的学生在意计算，25.6%的学生在意公式，都没有切中要害，16.6%的学生则注意是分割还是添补，有2名学生提出应该先求出图中未知的条件，仅有1名学生在意分割的准确性和整体性。经过访谈发现，有些学生只会计算已经画好分割线的组合图形的面积。

教学后，学生的算法呈现多样化，但是并没有寻求最优解的意识。这是因为笔者是顺着学生的思维，从众多方法中选择合适的开展教学，然后进行“三步走”：先算什么，再算什么，最后相加（或减）。因此，课后笔者不由得思考：为什么不将错误收集起来集体研究？为什么要逃避眼前的分歧？解决问题追求的不仅是答案的正误，重要的是解决问题过程中的探索与思辨。

鉴于以上原因，笔者重新设计了教学：收集学生的错误资源，并公之于众，集体讨论，将错误当成典型的反面教材，以作警示。

错误并不可怕，可怕的是对错误蕴含的教学价值视而不见。学生犯错必然是教师的教学存在盲区，如果教师一直按照基本模式出题，久而久之，学生就会形成路径依赖，一旦遇到变式问题，就会执拗地使用老方法，不知道根据各图之间的关联从已知的必要条件推出未知的必要条件，分割时不知道优化，不知道尝试不同的分割方式，找不到最优的分割方式……这些短板想靠习题训练补齐几乎不可能，因为题型千变万化，没有固定的模式可依，唯一的办法就是抓住一个错例深入挖掘和持续进行矫正训练。

三、教学实施及策略

1.正视错误，学会“留白”

例如，对于图3，学生尝试分解组合图形，先提出了横切法和纵切法（如图4和图5）；接下来，学生想到斜切法（如图6），这种错误分法令人猝不及防。

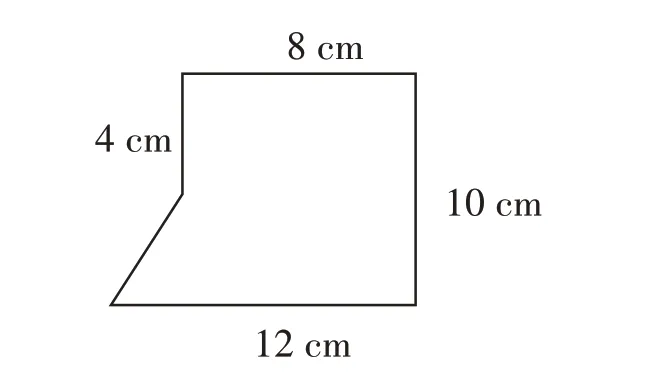
图3

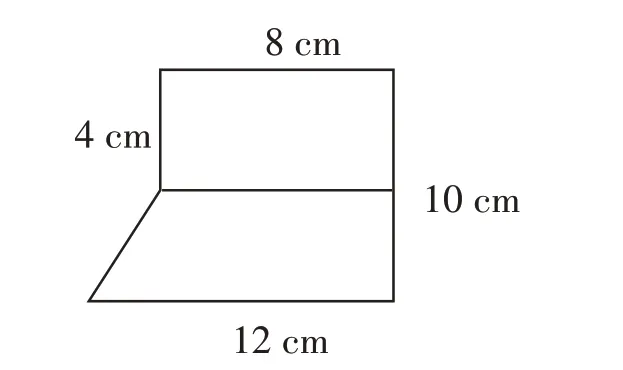
图4

图5

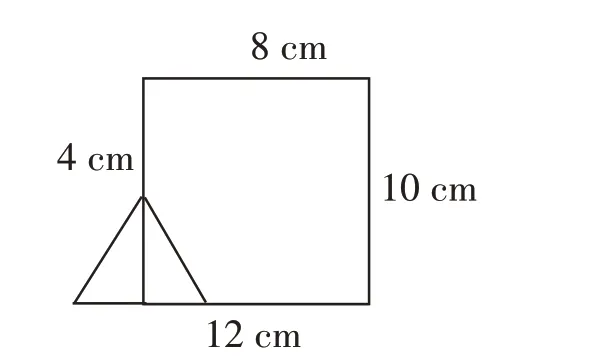
图6

“到底对不对？大家集体商讨。”笔者没有急着否定斜切法。

教室鸦雀无声。过了一会儿，有学生小声嘀咕：“这个好像不是梯形。”“对，这不是梯形！”支持的人渐渐多起来。笔者笑着问：“谁来具体说一说？”学生：“我觉得分割得出的图形算不上一个标准的梯形。”笔者继续说：“乍一看像一个梯形，但真相并非如此，被分出的不是一个基本图形，所以这种分法不合理。”

按惯例，笔者会不由分说马上推翻学生错误的想法，但这次则留白，让学生慢慢去观察对比。这个错误分法中确实存在合理因素，图6的右边部分貌似具有梯形的部分特征。对此进行辨析和充分讨论后，学生对梯形特征的认识就会更加清晰。

教师总是企图将错误的分割法扼杀在萌芽状态，刻意回避，生怕这种带有“歪理”的切割法会干扰学生的思维，影响教学秩序。殊不知，越是隐藏这种错误带来的危害就越大，学生思维中潜伏的错误因子会不定期爆发，就像一个定时炸弹威胁着其正常思维的发展，不如及早暴露及早解决。将错误推翻后，学生就会吸取教训，弥补思维缺陷。

2.容纳错误，让学生各抒己见

针对学生得出的图4、图5和图6，笔者追问：“还有别的分法吗？”一位学生画出了图7。这早在笔者预料之中。“到底对不对？”很快，就有学生发现了破绽：“下面的图形面积算不出来。”受他的提示，有学生幡然醒悟。“看来，这个图形不是一个常见图形，它的面积没有公式可依，这种分法不当。”他思忖一会儿，说：“再加一条线（如图8），可以补救。”这回得到大家的一致赞同。笔者继续追问：“这样分成了三个三角形，你们有异议吗？”有学生觉得烦琐。“如果能够分割成两个，就没必要分成三个自找麻烦了。”笔者又问：“分割时要遵循什么规则？”学生开始议论纷纷：“分割成的每个图形要有公式可依。分割得出的区块越少越好。”

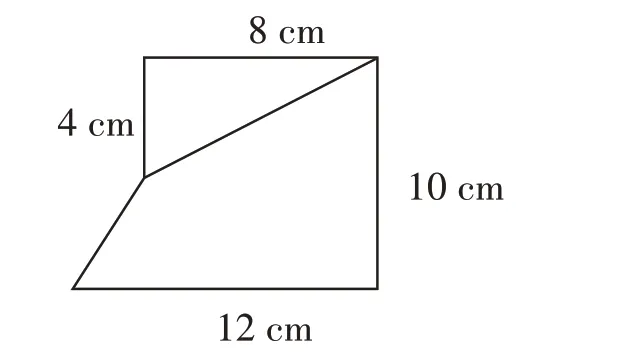
图7

学习中的困难和错误，有时正是智慧之光，教师既要宽待学生的错误，又要去剖析、补救和修正，在丝丝入扣的分析后，总结出“要根据条件尽量选择简单的方法”的解题策略。这样，学生学到的不仅是技巧，更是一种思想方法。同时，在集体商讨的过程中，学生互相取长补短，不断自我反思，不断改进方法，完善认知。最后，通过交流，学生学会了批判性地看待问题。

3.剖析错误，变废为宝

在学生修正错误后，笔者又问：“还有别的分法吗？”学生画出图9。“这样分，简单。”许多学生都认同这个方法。因为这种分法很有迷惑性，所以笔者让学生反思。“不对，简单是简单，但是无法计算面积。”果然，有学生看出漏洞。“为什么？”“这样分出的三角形的底就是一个无法推知的未知量。”“如此一来，三角形的面积有求解的可能吗？”“没有。”笔者继续追问：“梯形的面积有可能推算出来吗？”“不能，因为上底也成了一个永远无法知道的未知量。”这时，其他学生也醒悟了：“是的，这样就出现许多未知量，这种分法应该排除。”笔者继续追问：“那么，分割图形时还应满足什么要求？”学生纷纷发表意见：“所有的必要条件必须能够算出来。”“图形的底、高要知道。”……“很好，看来能够分成规则图形还不够，光简单也不够，还要可操作。”笔者总结道。

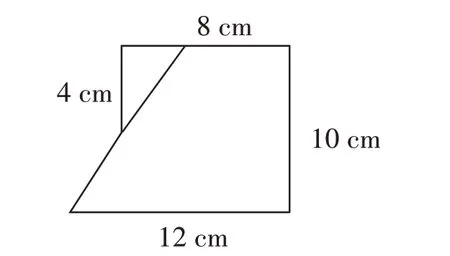
图9

对于这个意料之中的错误，教师让学生自己发掘，学生的思维能得到发散，就会想到更深层次的要求。这种错误带来了三方面的积极效果：纠正错误——学生发现分法的确简单，但是不具备操作性；学法指导——在分析错误的过程中，利用互评让学生不仅认识到错误，还找出错因；培养学习习惯——在辨析的过程中，要学会倾听别人的意见和观点，不断反思和完善自己的想法。

总之，错误总是与成长相伴左右的。面对学生的错误，教师要宽容，不能畏惧，而应顺着错误资源不断深挖彻查，让学生为了查找错因和修正错误而不断深入探究。