用于小型注塑件边缘提取的改进坎尼算法*

2022-09-30赵一鸣胡燕海

机械制造 2022年7期

□ 赵一鸣 □ 胡燕海

宁波大学机械工程与力学学院浙江宁波 315211

1 研究背景

随着塑料工业的发展,我国注塑制品年总产量已稳居世界第二,塑料产品成为人们生活中不可或缺的必需品。由于客观因素的影响,如原材料质量不佳、工艺水平较低、机械设备不稳定等[1],注塑件在生产过程中会出现大量问题,轻则影响自身外观,重则影响使用性能。如何检测注塑件的产品缺陷,是塑料行业密切关注的问题。目前,国内注塑件检测水平仍然不高,主要仍以人工检测为主,局限性较大[2]。基于图像处理技术,可以实现注塑件的自动检测,避免人为主观因素对检测结果的影响[3]。

在图像处理技术中,边缘提取是基本操作,边缘提取质量优劣直接决定后续图像特征信息提取的好坏。目前,已存在上百种提取目标物体边缘的方法。常用的一阶边缘提取算法有Roberts算法[4]、Sobel算法[5]、Scharr算法[6]等,常用的二阶边缘提取算法有拉普拉斯算法[7]、坎尼算法[8]等,这些算法的原理都是对图像与特定大小的模板进行卷积。其中,坎尼算法因卓越的边缘提取效果,在图像处理领域应用广泛。传统坎尼算法应用于小型注塑件的边缘提取时,若成像受到干扰,则各种噪声容易导致边缘提取精度降低[9]。小型注塑件的边缘提取对图像的细节像素要求较高,而传统坎尼算法非极大值抑制计算不够充分,细节像素会缺失。传统坎尼算法在实际运行前,往往需要凭借人为经验,对边缘提取的高低阈值进行设置,算法性能难以得到保证[10]。

笔者为满足行业和企业需求,针对传统坎尼算法应用于小型注塑件边缘提取时存在的问题,对传统坎尼算法进行改进,提出用于小型注塑件边缘提取的改进坎尼算法,由此在不使用其它算法的前提下,完成对小型注塑件边缘的完整提取。

2 传统坎尼算法原理

传统坎尼算法的流程一般如下:首先使用高斯滤波对图像进行预处理,去除图像中的噪点,并平滑图像;然后分别计算图像的梯度幅值与方向,对求得的边缘图像进行非极大值抑制;最后通过人为设置高低阈值,对阈值滞后的边缘像素点进行连接,得到检测目标的边缘信息[11]。传统坎尼算法流程如图1所示。

▲图1 传统坎尼算法流程

注塑件图像在采集、传送、成像过程中不可避免地会受到外部噪声干扰,如工厂灰尘、设备振动、光照不均匀导致反光等,这些噪声会降低边缘提取的效果。传统坎尼算法常搭配高斯滤波来去除噪声。高斯滤波对图像中的噪声具有一定滤除能力,但小型注塑件边缘提取对细节的要求较高,高斯滤波对细节的保留效果不够理想,卷积核尺寸如果过大,会将目标轮廓当作噪声一并滤除[12]。注塑件在生产过程中由于工艺水平参差不齐,往往存在一定缺陷,容易受到光照不均匀的影响而产生局部噪声,高斯滤波对这类噪声的滤除效果也难以满足实际检测需求。

传统坎尼算法采用差分运算法计算图像像素点的像素梯度,并采用欧氏距离与反正切函数来计算像素点的幅值方向。

非极大值抑制是传统坎尼算法将图像目标边缘细化的方法。经前序流程处理后得到的边缘往往含有多个像素,通过非极大值抑制可以将局部最大梯度值对应的像素点予以保留,并滤除剩余像素。但是,非极大值抑制参与的梯度方向不够全面,导致边缘的连续性不佳,这对小型注塑件边缘提取精度造成了一定影响。

经过非极大值抑制后,虽然剩余的像素可以用于较为准确地提取注塑件实际轮廓,但是仍然存在一定的杂散响应。为解决这一问题,传统坎尼算法由人为设定高低阈值。高低阈值将图像信息分割为三个部分,真实边缘部分对应大于高阈值,伪边缘部分对应介于高低阈值之间,非边缘部分对应小于低阈值,然后将非边缘部分的像素点滤除。在实际应用中,需要凭借人为经验设定高低阈值,重复多次试验才能确定较为合理的阈值。由于外界因素导致工作条件改变时,又需要重新调整阈值。由此,传统坎尼算法实际应用时将耗费大量时间,有必要进行改进。

3 滤波改进

针对高斯滤波对小型注塑件图像细节保留不充分的问题,考虑使用双边滤波替代。与高斯滤波不同,双边滤波不仅考虑图像灰度值大小,而且考虑像素的欧氏距离,在滤除噪声的同时使边缘细节信息不容易丢失[13]。双边滤波计算式如下:

(1)

(2)

(3)

式中:f(m,n)为滤波处理前图像中坐标点(m,n)的灰度值;f(i,j)为滤波处理后图像中坐标点(i,j)的灰度值;v为以坐标点(i,j)为中心,以2r+1为边长的正方形窗口内所有像素坐标点的合集,r为滤波窗口半径;ωr(m,n)为坐标点(m,n)的灰度值相似度权重;ωd(m,n)为坐标点(m,n)的空间权重;σd为空间标准差;σr为灰度标准差。

双边滤波对图像的细节保留较为完整,但是在遇到一定程度的强噪声时,容易将噪声像素当作边缘一同保留。强噪声与中心像素的灰度差值较大,计算获得的灰度值相似度权重也往往较大。中值滤波对强噪声的滤除效果极佳,计算原理如图2所示。

▲图2 中值滤波计算原理

中值滤波将矩阵内所有像素根据灰度值从小到大排列,矩阵中心像素由序列中值替代,将滤波矩阵以中心像素点为基准移动至下一个位置,如此重复操作。中值滤波不会受到灰度值过大或过小像素点的影响,对强噪声具有较好的滤除效果。另一方面,一旦中值滤波的尺寸过大,则会造成细节边缘模糊,同样在图像细节保留方面效果欠佳。对此,考虑采用一种能够根据噪声分布密度自动调整滤波尺寸大小的自适应中值滤波,并与双边滤波进行组合。自适应中值滤波流程如图3所示,其中Wxy为以坐标点(x,y)为中心的窗口大小,Gmax为Wxy中的最大灰度值,Gmed为Wxy中的灰度值中值,Gmin为Wxy中的最小灰度值,Gxy为坐标点(x,y)的灰度值大小,Wmax为窗口的最大尺寸。

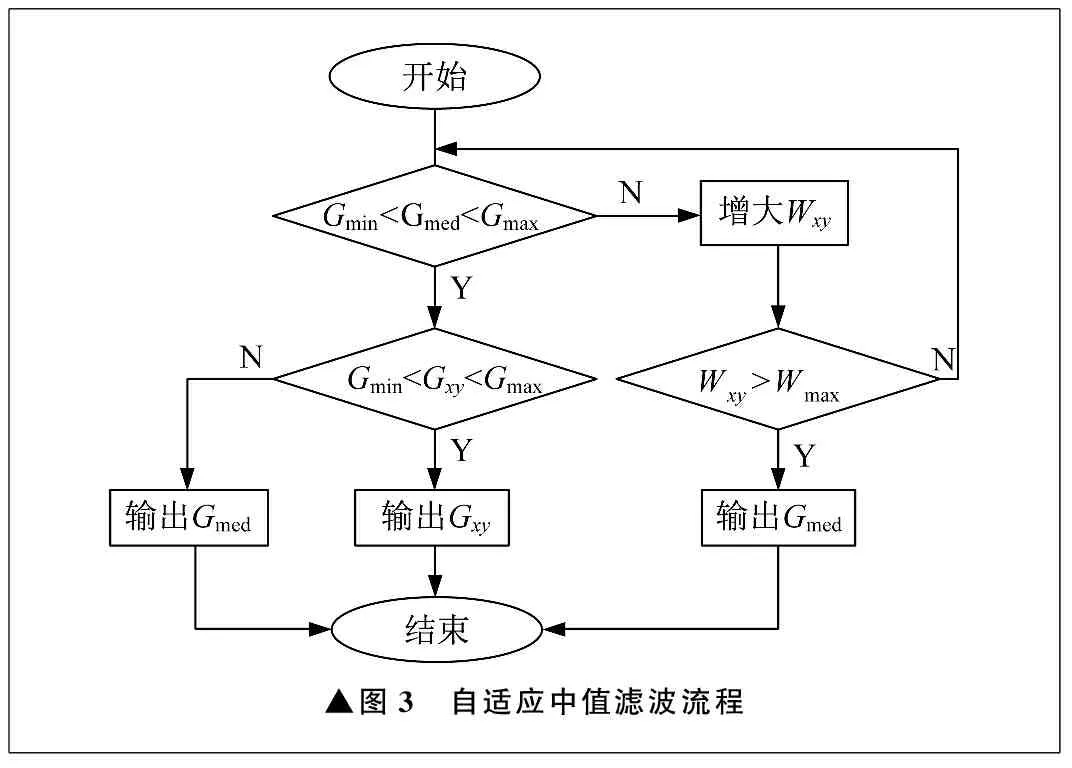
▲图3 自适应中值滤波流程

进行组合滤波时,先进行自适应中值滤波,将强噪声滤除,再进行双边滤波,滤除剩余噪声。

4 非极大值抑制改进

针对非极大值抑制时参与的梯度方向不够全面,导致小型注塑件边缘提取连续性不佳的问题,考虑基于原有梯度方向,新增22.5°、67.5°、112.5°、157.5°、202.5°、247.5°、292.5°、337.5°梯度方向,梯度方向如图4所示。

▲图4 梯度方向

通过计算各方向上欧氏距离的大小,将距离最近的像素点归为同一梯度方向予以保留。设像素点p的坐标为(i,j),像素点q的坐标为(x,y),像素点p和q之间的欧氏距离S(p,q)为:

(4)

5 高低阈值判别改进

针对凭借人工经验设定高低阈值需多次重复试验而造成效率低的问题,考虑采用遗传算法对高低阈值选取进行优化。遗传算法是一种通过模拟自然进化过程搜索最优解的方法,流程如图5所示。

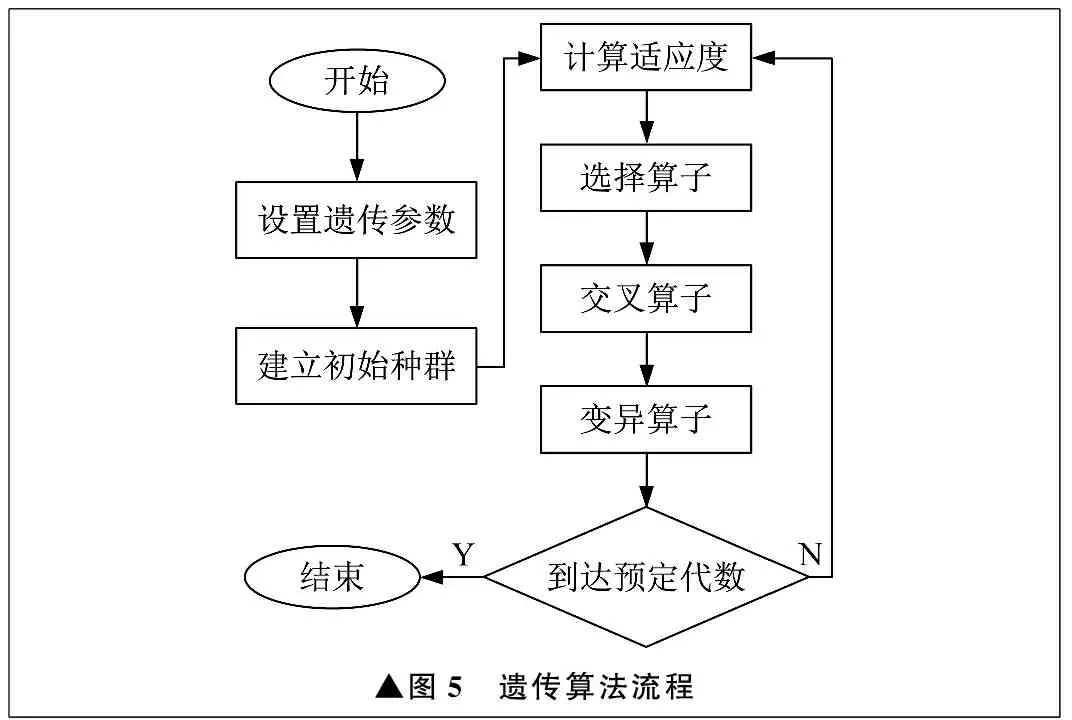
▲图5 遗传算法流程

以最大类间方差公式作为遗传算法的适应度函数,确定最佳高低阈值的评价指标。

图像灰度值为0～255,个体通常采用二进制编码。由于传统坎尼算法要求设置高低两个阈值,因此用16位二进制数对个体进行编码,前后各8位分别表示高低阈值,初始种群数目设为50。

最大类间方差法是一种基于全局的二值化算法,不仅处理迅速,而且不易受图像亮度和对比度的影响。设图像总像素数为N,灰度值范围为0～L-1,对应灰度级i的像素数为ni,则概率pi为:

pi=ni/Ni=0,1,2…,L-1

(5)

(6)

将像素点按灰度阈值T分为C0和C1,C0由灰度值为0～T的像素点构成,C1由灰度值为T+1～L-1的像素点构成。C0对应图像的非边缘部分,C1对应图像的真实边缘部分。整幅图像的灰度值平均值uT为:

(7)

C0和C1的灰度值平均值u0、u1分别为:

(8)

(9)

C0和C1的灰度分布概率w0、w1分别为:

(10)

(11)

于是有:

uT=w0u0+w1u1

(12)

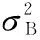
(13)

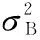
f=w1w0(u0-u1)2

(14)

传统遗传算法的交叉概率是一个固定值,并且一般在0.4～0.9之间取值,但固定的交叉概率容易导致最终求得的解与实际最优解不符。笔者将交叉概率由固定值改为进化代数到一定值后发生改变。在进化早期提高交叉概率,避免淘汰个体太多而陷入局部最优解。在进化中后期降低交叉概率,加快收敛速度,以提高求解效率。交叉概率Pc为:

(15)

式中:gen为进化代数。

6 试验分析

为验证改进坎尼算法对小型注塑件边缘提取的可靠性,模拟工厂实际加工环境,采集多幅图像,直接调用传统坎尼算法进行对比试验。计算机配置英特尔酷睿i7-1065G7中央处理器,运行内存为16 GiByte,安装视窗10操作系统,编程环境为Visual Studio 2017,编程语言为C++。遗传算法中最大进化代数设置为200,变异概率设置为0.01,滤波器尺寸均调节至同一大小,高低阈值设置传统坎尼算法与改进坎尼算法一致,其它参数同前文。图像1如图6所示,图像2如图7所示,图像3如图8所示,图像1算法对比如图9所示,图像2算法对比如图10所示,图像3算法对比如图11所示。

▲图6 图像1▲图7 图像2▲图8 图像3

▲图9 图像1算法对比▲图10 图像2算法对比▲图11 图像3算法对比

由算法对比可知,图像在背景存在一定灰尘和光照不均匀干扰时,传统坎尼算法对小型注塑件边缘提取的效果较差,噪声难以被滤除,边缘的连续性较差,在对小型注塑件添加标记模拟缺陷并随意摆放后,边缘存在大量断裂,难以反映小型注塑件的真实边缘情况,改进坎尼算法在对小型注塑件进行边缘提取时则不存在以上问题。

以下从信噪比、单边响应原则、算法耗时三个方面对传统坎尼算法与改进坎尼算法的性能进行对比。

信噪比作为图像量化评价指标,表示真实边缘点与噪声的比值。信噪比SNR为:

(16)

式中:f(x)为-w～w内的滤波脉冲响应;G(-x)为边缘函数;σ为噪声均方差。

噪声均方差越大,表示有效边缘越多,噪点越少。

信噪比对比见表1,可见改进坎尼算法对小型注塑件边缘提取时抗噪性明显提高。

表1 信噪比对比

采用文献[14]的边缘评估方法,统计图像的边缘像素总数A、四连通域数B、八连通域数C,单边响应原则试验对比见表2。C/A越小,表示边缘图像的间断越少,连续性越好。C/B越小,表示边缘图像的单边缘响应效果越好。由表2可见改进坎尼算法对小型注塑件边缘提取连续性和准确性相比传统坎尼算法有一定提升,更有利于后续对图像进行分析。