高分子囊泡在微管流中惯性迁移现象的有限元分析*

郝鹏 张丽丽 丁明明2)†

1) (伊犁师范大学物理科学与技术学院,新疆凝聚态相变与微结构实验室,伊宁 835000)

2) (广东工业大学轻工化工学院,广州 510006)

采用基于流固耦合的有限元方法,对二维模型中高分子囊泡在微管流中惯性迁移现象进行了系统研究,分析了囊泡因受到流体作用力而形变并发生惯性迁移现象的机理.研究表明: 随着雷诺数的增大,囊泡惯性迁移的平衡位置离其初始位置越来越远;随着阻塞比的增加,囊泡惯性迁移后的平衡位置越来越接近壁面.对于囊泡膜的模量和黏度以及膜厚,结果表明模量和黏度决定了囊泡的变形程度,模量对囊泡平衡位置影响较小,但增大黏度和膜厚会促进囊泡的平衡位置偏向管道中心.本研究有助于进一步明晰囊泡在惯性迁移过程中的形变和平衡位置,为囊泡在药物输运、化学反应和生理过程的应用提供可靠的计算依据.

1 引言

囊泡是由两亲性分子有序组合且具有双层膜结构的一种组合体,其大小约为30 nm—100 µm,呈圆形或椭圆形.双层膜内外通常为简单的黏性液体,在新陈代谢、物质输运、免疫识别、浮力调节、酶存储与释放等过程中发挥重要作用[1-3].由于囊泡膜与细胞膜的结构非常相似,所以其作为简单生物膜模型而得到广泛的研究[4].

惯性迁移指随机分布在微通道中的粒子与流体相互作用之后,达到指定的平衡位置,并平行于壁面移动.惯性微流控技术[5-6]是一种能够实现颗粒或细胞高通量精确操控的新方法,广泛应用在生物、医学、材料和环境等领域.惯性迁移原理是惯性微流控技术的核心,因此许多学者对微颗粒在流体中的动力学行为进行了广泛的研究,例如刚性小球[7-9]、囊泡[10]、胶囊[11-12]或红细胞[13-15]等.

最初,Segré和Silberberg[16]通过实验发现: 在圆管层流中,球形颗粒惯性迁移后的平衡位置约为管道半径0.6 倍处的圆环区域,称为“管缩效应”.Segré和Silberberg 及之后的研究者认为引发颗粒聚集的升力是由流场的惯性作用而产生的,因此被称为颗粒惯性聚集现象.Carlo 等[17-18]采用模拟方法描述了较大中性悬浮颗粒的动力学行为,揭示了升力与通道和颗粒几何形状的复杂关系.本质上,颗粒在微管流中惯性迁移是剪切梯度升力(指向通道壁面[19])和壁面诱导升力(指向通道中心[20])两者相互平衡的结果.Carlo 等[21]研究了管道壁面、雷诺数及弯曲管道二次流等因素对细胞或颗粒惯性迁移的影响.Asmolov[7]研究了大雷诺数时刚性小球以及中性和非中性粒子的惯性迁移问题,采用匹配渐近展开的方法推测颗粒的平衡位置,研究表明曲率对无扰动速度分布的影响是显著的,在大雷诺数下,升力的值与线性剪切流对应的值不同.Matas 等[8]研究了雷诺数为67—1700 的泊肃叶流中悬浮粒子的迁移规律,并验证了Segré-Silberberg[16]的理论,证明了粒子的管状捏缩效应,并观察到大雷诺数颗粒的迁移位于Segré-Silberberg 平衡位置[9].Morita 等[22]同样验证了Segré-Silberberg 提出的理论,并证明了随着雷诺数增加,管道的入口长度对颗粒平衡位置的影响随之增强.Yao 等[23]发现颗粒在高雷诺数圆管流体中会出现内外两个平衡位置.Nakayama 等[24]对圆管中悬浮颗粒进行数值模拟和实验测量发现随着雷诺数增加,不同颗粒惯性聚集平衡分布,存在三个区域与之相对应.

除了以上考虑的硬颗粒,国内外学者对“软颗粒”,如囊泡等在微管流中的动力学行为也做了许多有意义的研究[25-28].Shin 等[29]采用二维数值模拟方法发现: 当囊泡膜的弹性确定时,其最终平衡位置随雷诺数的变化而变化.然而,Alghalibi 等[30]发现软颗粒直径是管道直径的0.2 倍时,颗粒的平衡位置与颗粒的柔软程度或流速无关,总是停留在管道中心.Kruger 等[31]发现,当雷诺数和毛细数足够大时,软粒子与软粒子相互作用增强了其向通道中心的迁移.Hur 等[32]通过实验发现不同弹性和黏度的颗粒和液滴具有独立的横向动态平衡位置,即在通道中粒子可以彼此分离.

尽管“软”“硬”颗粒在微通道中的动力学行为受到了学者们的广泛关注,但目前关于囊泡的研究缺少对膜黏性的考虑.例如,聚合物构成的囊泡,依赖于聚合物网络的交联密度[33],可增加几何性和机械性.此外,膜的黏弹性和收缩性取决于膜的成分和制备工艺[34].弹性囊泡忽略了膜黏度,其平衡位置由壁效应和剪切梯度效应之间的平衡决定[35].但是聚合物囊泡的黏性特征尤为显著,势必会影响囊泡在惯性迁移中的形变和平衡位置,因此,研究囊泡的黏弹性对其惯性迁移的影响具有重要意义.

本文采用基于流固耦合的有限元方法对黏弹性囊泡在微管流中的惯性迁移现象进行了系统研究,计算发现,囊泡受到流体的挤压会发生形变,从圆形变为椭圆状.当雷诺数Re＜50 时,囊泡惯性迁移现象不明显,但是随着雷诺数的增加,囊泡惯性迁移的径向位移越来越大,达到平衡位置后,保持一定的形状平行于壁面移动.囊泡膜黏度的增大使得其惯性迁移后的平衡位置向管道中心偏移,但随着囊泡阻塞比的增加,囊泡惯性迁移的平衡位置越来越接近管道边缘.控制影响囊泡惯性迁移的不同因素可以有效地确定其最终平衡位置,有助于实现精准分离.

2 仿真模型与有限元分析

如图1 所示,在前期工作基础上[36-42],通过二维模型计算囊泡在微管流中惯性迁移行为.当流体流过囊泡时,会在囊泡表面施加一个垂直于流动方向的分力,称为升力.升力分为壁面诱导升力和剪切梯度升力.剪切梯度升力指颗粒在管道流中由于流体速度分布引起的力,即当流体绕过颗粒时,由于颗粒表面上下速度差所产生的力(通常指向通道壁面或者剪切率增加的方向).壁面诱导升力指颗粒靠近壁面时,由于流体压强会对颗粒产生远离壁面方向的力,其随着颗粒与壁面之间距离增加而减小[43].

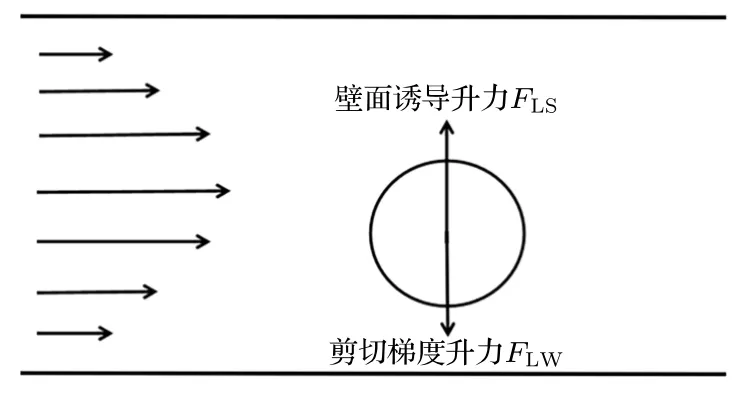
图1 囊泡受力分析图(剪切梯度升力指向通道壁面,壁面诱导升力指向通道中心)Fig.1.Vesicle force analysis.(Shear gradient lift points to the channel wall,wall-induced lift points to the channel center).

图2 是囊泡在微管流中惯性迁移的示意图,管道内流体假定为水,密度ρ为1000 kg/m3,黏度µ为0.001 Pa·s,且认为是不可压缩牛顿流体.水的流动采用湍流k-ε模型描述,矩形上下壁面为无滑动条件,左右两边为开放边界,左边为入口,初始流速为V,右边为出口,由此形成微管内水的流动.可变形囊泡假设具有黏弹性,置于管道内部.图2(b)—(d)展示了不同时刻囊泡周围流速的分布以及囊泡自身的形变.

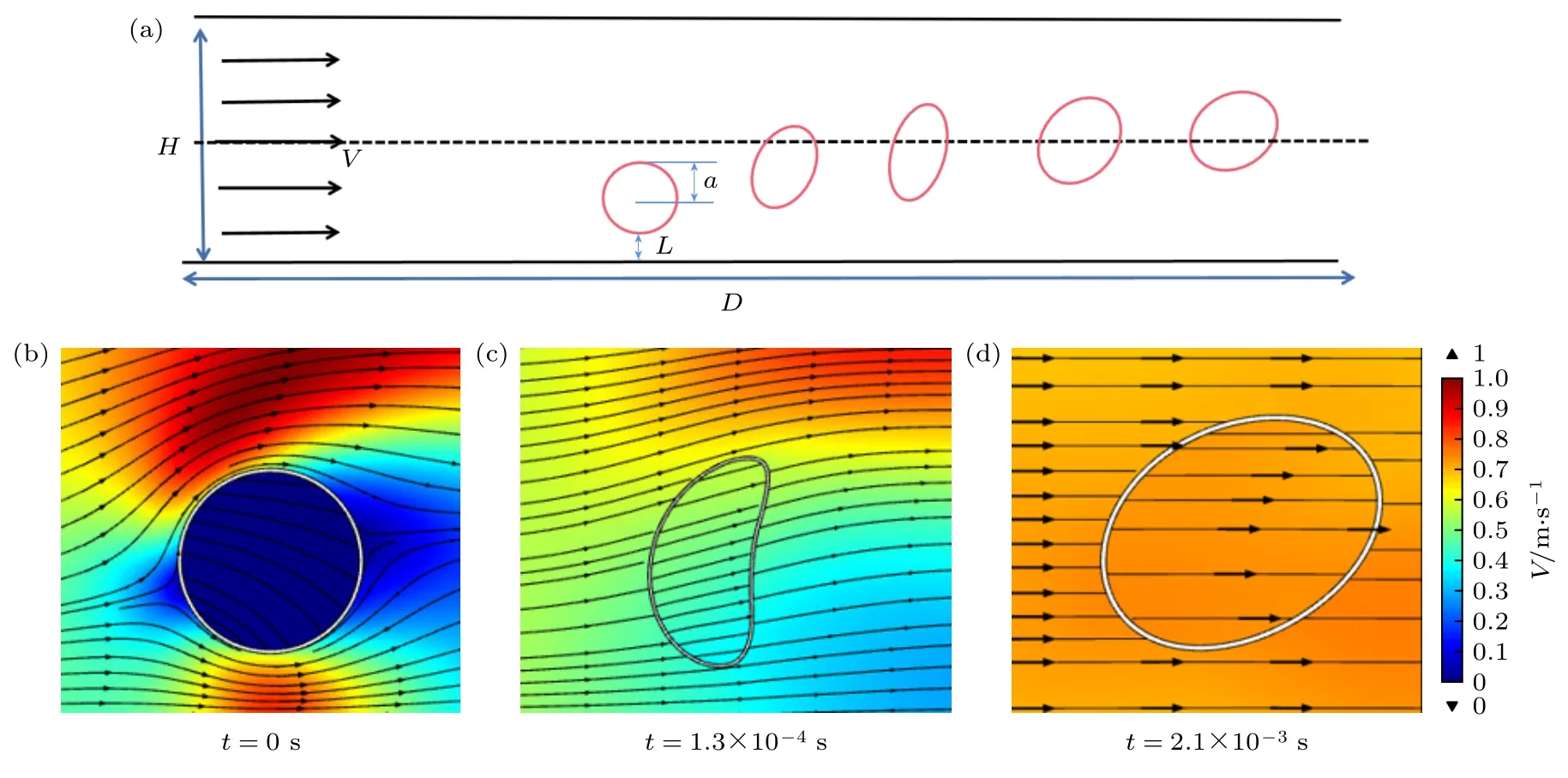
图2 (a) 囊泡惯性迁移示意图;(b)—(d) 不同时刻囊泡周围流速图 (管道宽为H=150 µm、长为D=1300 µm,囊泡半径为a=20 µm,囊泡膜厚1 µm,囊泡内外均为水.膜的杨氏模量为5000 Pa.管道入口速度为V,囊泡表面到管道壁面的距离为L)Fig.2.(a) Schematic representation of the vesicle inertial migration;(b)—(d) flow velocity around vesicles at different times (The channel width is H=150 µm and length is D=1300 µm.The vesicle radius is a=20 µm and the vesicle membrane is 1 µm thick.Water is both inside and outside the vesicles.The Young’s modulus of the membrane is 5000 Pa.The inlet speed is V,L is distance from the vesicle surface to the channel wall).

微管流中不可压缩流的连续方程和运动方程为[36]

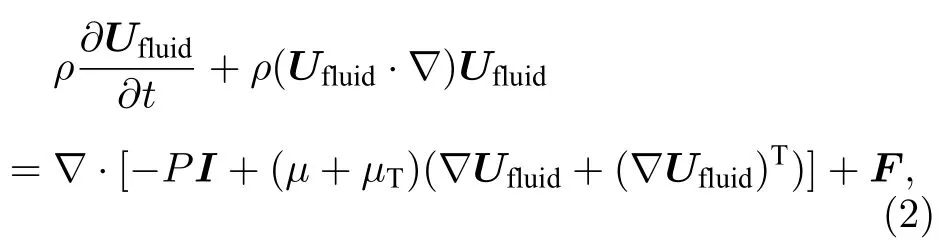
式中,F为外力;∇表示(∂/∂x,∂/∂y);Ufluid为流速;I为单位矩阵;P为压力.

假设囊泡膜具有黏弹性,其运动描述如下[42]:

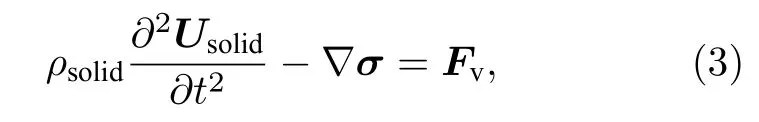
其中ρsolid为膜密度,Usolid为位移,σ为应力张量,Fv为单位体积的力.用Kelvin-Voigt 模型描述囊泡膜的黏弹性行为,其弹性应变率和应力张量的关系为[39]

式中η=0.022 Pa·s 为膜黏度;ε为膜应变张量[39],

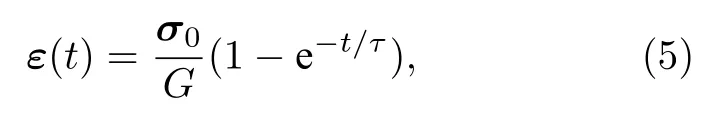
其中τ为松弛时间[39],

G为剪切模量[39],

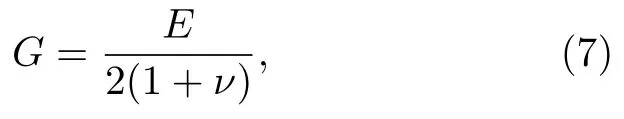
E=5000 Pa 是杨氏模量,ν=0.33 是泊松比.

对于囊泡膜的变形与迁移,变形指数γ和水平速度vx、垂直速度vy分别为[39]

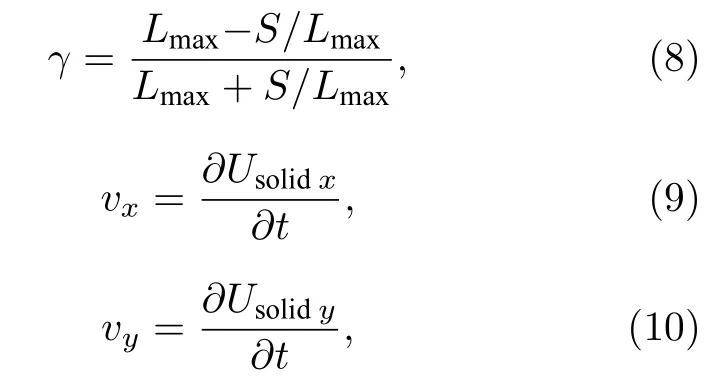
其中Lmax是囊泡质心到囊泡表面的最大距离;S是囊泡膜包围的面积;Usolidx和vx是囊泡的水平位移和速度,相对而言Usolidy和vy是囊泡的垂直位移和速度.

考虑到囊泡运动后形状变化,其在不同时刻的倾向角θ变化可表示为[39]

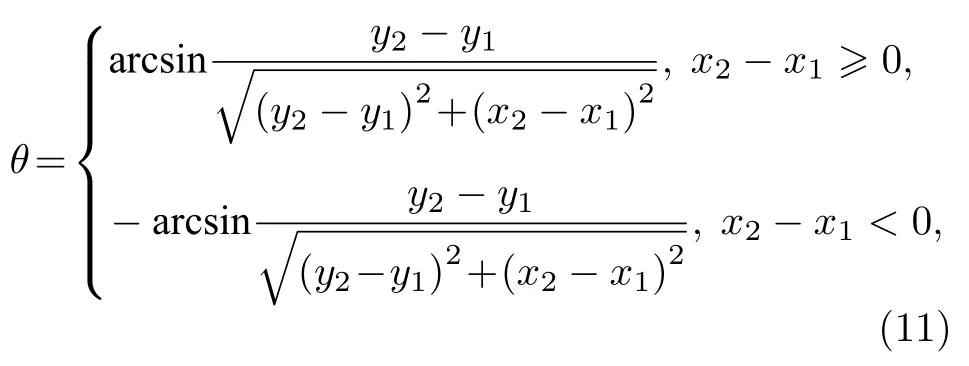
式中,(x1,y1)表示囊泡质心坐标;(x2,y2)表示囊泡膜上离质心最远点的坐标.

采用流固耦合计算流体和囊泡膜的相互作用,边界处的相互作用可以表示为[36]

其中vw是囊泡膜的速度,n为流固界面的单位法向量,Γ为流体施加在囊泡边界上的总力.因此,流体受到囊泡的反作用力为反方向.

体系雷诺数为Re=ρvd/u.根据以上参数,本文雷诺数范围为1＜Re＜400.在COMSOL Multiphysics 5.3a 软件中,利用有限元方法来求解非结构网格上的控制方程.采用任意拉格朗日-欧拉方法计算囊泡膜和流体网格节点的移动变化以及求解流固耦合有关方程[35].为了提高计算精度和收敛性,减少计算时间,采用自由三角网格来提高网格质量并且对网格进行细化,且自动重新划分网格以避免由流固相互作用导致的网格质量问题[44,45].

3 结果及分析讨论

3.1 阻塞比、雷诺数和初始位置对囊泡惯性迁移的影响

计算过程中,首先观察到囊泡形状的变化,从圆形变为半月形,再由半月形变为椭圆形,并保持椭圆状以一定的倾向角平行于壁面移动,如图2(b)—(d)所示,这与之前的研究结果一致[46-47].第一次形变由于流体挤压囊泡促使其形变,且形变随着雷诺数的增加而增大.第二次形变由囊泡第一次形变后,囊泡膜积累了弹性应变能,促使囊泡拥有恢复原先形状的能力.此外,囊泡运动过程中,由于管道流中囊泡表面上下速度差,使得囊泡向受力大的方向偏移,直到达到平衡(即垂直速度为零).

如图3 所示,计算了囊泡初始质心距壁距离40 µm 时的惯性迁移行为,其中囊泡阻塞比κ=a/h定义为囊泡半径与管道宽度一半之比(ɑ为囊泡半径,h为管道宽度一半).结果表明,不同阻塞比下,随着雷诺数的增大,囊泡表现出完全不同的迁移行为.当k=0.1 时,随着雷诺数的增加,囊泡惯性迁移后的平衡位置逐渐趋于管道中心.然而,当k=0.3 时,随着雷诺数的增加,囊泡的平衡位置开始趋向管道中心,但随着雷诺数的进一步增大,开始向管道边缘靠近.此外,当k=0.5 时也取得了相似的结果.因此,改变雷诺数或颗粒阻塞比都可以显著改变囊泡的最终平衡位置.此外,Matas等[8]实验报道中颗粒的阻塞比范围约为0.0238—0.125 时,如图3 虚线所示,随着雷诺数的增加,颗粒偏向管道中心,这与本文软球颗粒阻塞比为0.1时,囊泡惯性迁移平衡位置规律相似.

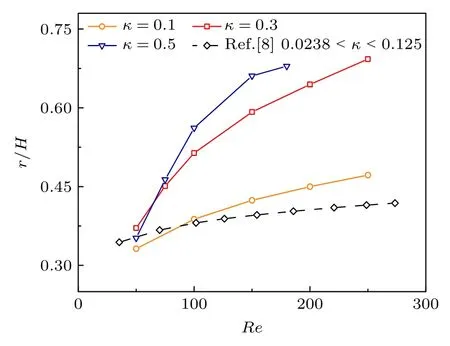
图3 不同阻塞比下,雷诺数对惯性迁移平衡位置的影响(r 代表囊泡达到平衡位置后质心的纵坐标.黑色虚线代表Matas 等[8]的实验报道结果,其颗粒直径为190 µm—1 mm,管道宽度为8 mm,即颗粒的阻塞比范围为0.0238—0.125)Fig.3.Effect of Reynold numbers on the equilibrium position of inertial migration with different blocking ratios (r represents the ordinate of the centroid of the vesicle after reaching the equilibrium position.The black dashed line represents the experimentally reported results of Matas et al.[8]with particle diameters of 190 µm—1 mm and pipe widths of 8 mm,i.e.the particle blocking ratios ranged from 0.0238 to 0.125).

理论上,颗粒在微管流中惯性迁移是剪切梯度升力[19]和壁面诱导升力[20]两者相互平衡的结果.为了能够进一步阐释不同阻塞比和雷诺数时囊泡平衡位置的差异,计算囊泡升力随时间的变化图.如图4(a)所示: 当雷诺数Re=100 时,随着颗粒阻塞比的增加,囊泡受到的升力越大.因此,囊泡尺寸会改变囊泡受到的升力大小,进而影响平衡位置.如图4(b)所示: 当阻塞比k=0.3 时,囊泡受到的升力随着雷诺数的增加而增加.因此,雷诺数也是改变囊泡平衡位置的重要因素.此外,无论初始升力存在多大差异,最终都趋于零,即囊泡达到平衡位置.其次,发现随着雷诺数和颗粒阻塞比的增加,囊泡达到平衡的时间越久,这也为不同颗粒进行筛选和分离提供了时间窗口.

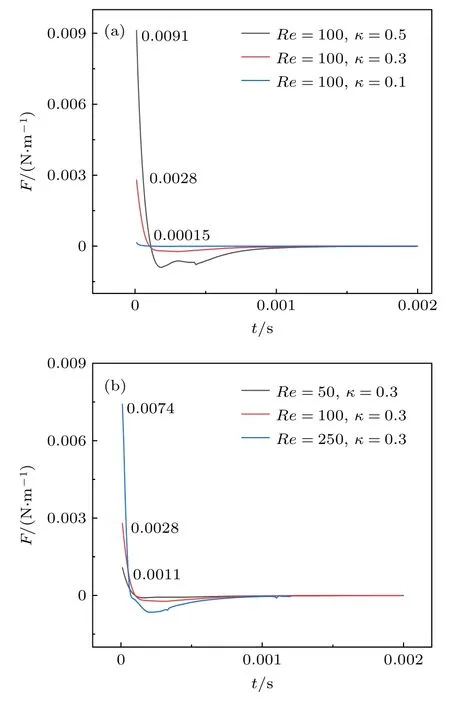
图4 不同雷诺数和阻塞比下囊泡升力随时间的变化图(a) Re=100,k=0.1,0.3,0.5;(b) Re=50,100,250,k=0.3 (F 为升力,即是壁面诱导升力与剪切梯度升力的总和,方向为管道径向)Fig.4.Plot of vesicle lift over time under different Reynolds numbers and blocking ratios: (a) Re=100,k=0.1,0.3,0.5;(b) Re=50,100,250,k=0.3 (Lift is the sum of wall-induced lift and shear gradient lift,in the tube radial).

进一步计算了囊泡初始位置对其惯性迁移规律的影响.计算结果发现: 囊泡初始位置对其最终平衡位置影响显著.如图5 所示,阻塞比k=0.32、模量E=5000 Pa 时,不同初始位置导致囊泡惯性迁移后平衡位置发现明显变化.当L=51 µm时,即位于管道中心时,随着雷诺数的变化,其平衡位置始终处于管道中心,没有发生偏移.然而,当初始位置L=31 µm 时,也就是处于管道一侧时,结果表明囊泡随着雷诺数的增加,呈现先趋于管道中心聚集而后开始向管道壁侧迁移.随着初始位置向管道壁侧移动,这一现象更加明显,例如L=1 µm 时,即初始时刻靠近管道壁,随着雷诺数的增加,其最终平衡位置变化显著.此外,发现当L=11 µm 时,随着雷诺数的增加,囊泡迁移后的平衡位置趋壁现象最明显,甚至大于L=1 µm 的情况.因此,分析了不同初始位置时囊泡惯性迁移过程中所受力的变化.结果表明,囊泡初始位置距壁距离L=11 µm (L/H≈0.1,即约为管道宽度的1/10)时,产生的升力最大,从而导致囊泡惯性迁移的平衡位置更靠近管道壁面.

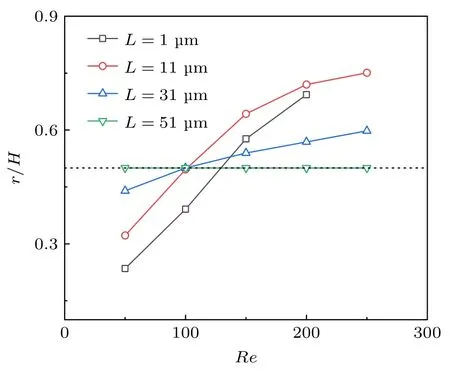
图5 囊泡初始位置对惯性迁移的影响Fig.5.Effect of the initial vesicle position on the inertial migration.

为了验证囊泡初始距壁距离为11 µm 时,升力最大这一观点,描述了雷诺数为50 和200 时,囊泡的初始位置不同,其升力随时间的变化图,如图6(a)和图6(b)所示,结果表明囊泡初始距壁距离L=11 µm 时,升力最大.

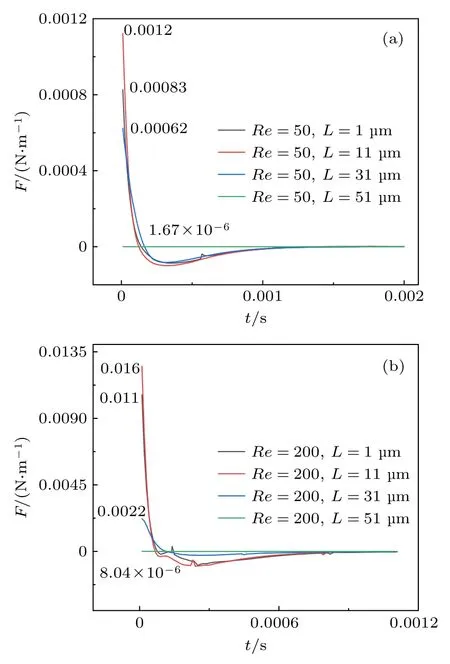
图6 不同初始位置时囊泡升力随时间的变化 (a) Re=50;(b) Re=200Fig.6.Variations of vesicle lift with time at different initial positions: (a) Re=50;(b) Re=200.

以上结果表明,囊泡的初始位置、阻塞比和雷诺数是影响其平衡位置的关键因素,通过联合调整相应参数,可实现对平衡位置的控制,进而实现精确筛选.

3.2 囊泡膜的模量、黏度和膜厚对惯性迁移的影响

囊泡膜的模量和黏度是表征膜特性的两个最重要参数,因此也势必会影响其惯性迁移规律.模量决定着囊泡膜的变形难易程度,因此,选取囊泡膜初始位置距壁距离L=16 µm,阻塞比k=0.32,膜厚1 µm 进行分析计算,如图7 所示,随着模量的增加,囊泡平衡位置几乎没有任何变化.然而,也注意到当Re=350 时,不同模量的囊泡的平衡位置有了差异.但由于模型收敛性的限制,没能进一步计算更大雷诺数的情况.

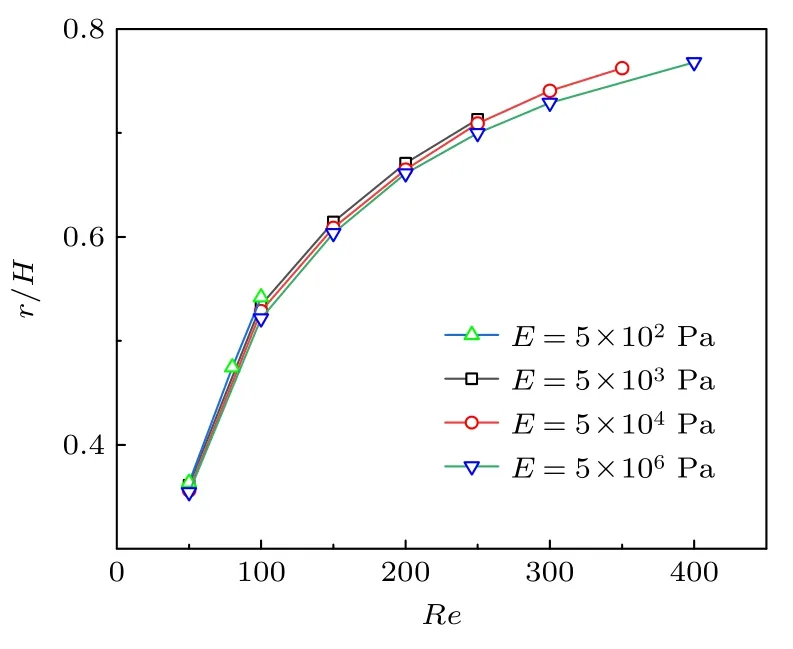
图7 囊泡膜模量对惯性迁移的影响Fig.7.Effect of the modulus of vesicle membrane on the inertial migration.

对于许多囊泡,尤其是高分子类的囊泡,膜的黏性是一个无法忽略的属性.已有研究表明,利用高分子囊泡模拟细胞的动力学过程中,最重要的一点是细胞膜的黏度,增加膜的黏度可以减弱软颗粒或生物细胞的变形[48].分析了囊泡形变及其惯性迁移的轨迹,囊泡形变越大表示其受力越大,促使其平衡位置朝向管道壁面移动.图8 描述了不同黏度η时,囊泡形变及其迁移的轨迹(补充文件图S1和图S2 (online)给出了不同膜量和模厚的计算结果).在图8 中描述了黏度η=1 和100 Pa·s 时,囊泡惯性迁移过程的形变和平衡位置轨迹图以及囊泡所受最大升力.从图8 可以明显地看出,增大膜黏度可以抵抗因受流体作用力而发生的形变,并使得囊泡升力减小导致其平衡位置降低.

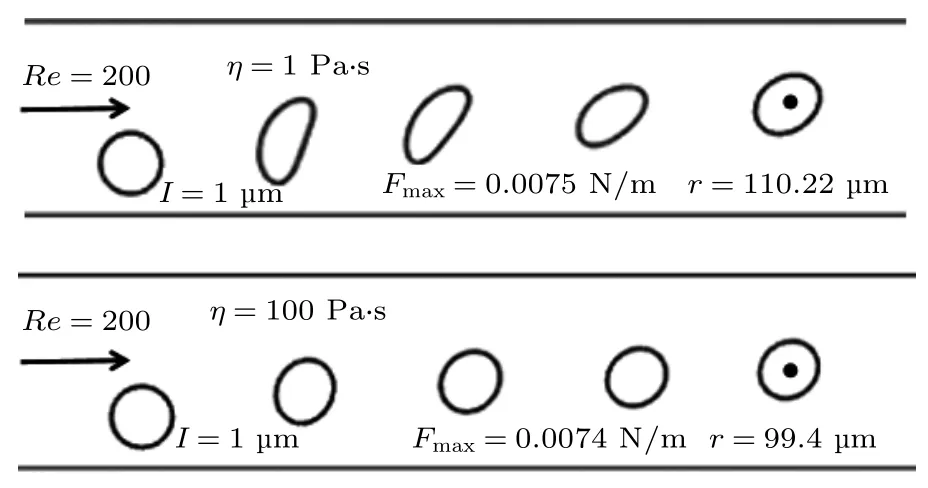
图8 不同膜黏度时囊泡的形变及其迁移位置轨迹图Fig.8.Deformation of vesicles and their migration location trajectories at different membrane viscosities.

其次,计算了模量E=10000 Pa,阻塞比为0.32,囊泡膜初始距壁距离L=16 µm 时,不同膜黏度η对囊泡惯性迁移的影响.如图9 所示,在所计算的黏度和雷诺数区间,囊泡惯性迁移后的平衡位置向管道中央偏移.这主要可归因于黏度会改变囊泡在流体中的形变,进而影响受力情况,从而出现了规律性偏向管道中心的现象.

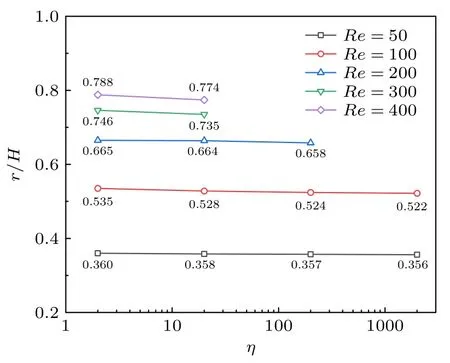
图9 囊泡膜的黏度对惯性迁移的影响Fig.9.Effect of vesicle membrane viscosity on the inertial migration.

最后,还计算了模量5000 Pa,阻塞比为0.32,囊泡膜初始距壁距离L=16 µm 时,不同膜厚度I对囊泡惯性迁移的影响.如图10 所示,在计算的雷诺数区间,观测到随着囊泡膜厚度的增加,囊泡惯性迁移后的平衡位置趋向管道中心.

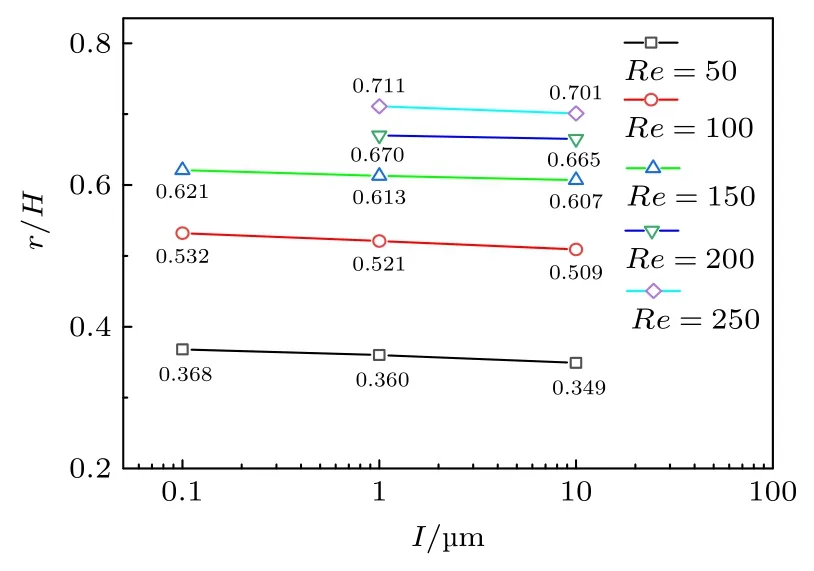
图10 囊泡膜厚对惯性迁移的影响Fig.10.Effects of vesicle membrane thickness on inertial migration.

4 结论

高分子囊泡在微管流中惯性迁移现象的规律是应用惯性微流控技术实现其分离的重要基础.本文采用基于流固耦合的有限元方法对高分子囊泡在微管流中惯性迁移现象进行了系统研究,分析了囊泡因受到流体作用力而形变并发生惯性迁移现象的机理.研究表明: 随着雷诺数的增大,囊泡惯性迁移的平衡位置离其初始位置越来越远;随着阻塞比的增加,囊泡惯性迁移后的平衡位置越来越接近壁面.此外,模拟还发现当初始位置约为管道宽度的1/10 时,囊泡受到的升力最大,从而导致囊泡惯性迁移的平衡位置更靠近管道壁面.对于囊泡膜的模量和黏度,结果表明模量和黏度决定了囊泡的变形程度,模量对囊泡平衡位置影响较小,但增大黏度和膜厚会促进囊泡的平衡位置偏向管道中心.本研究有助于进一步明晰囊泡在惯性迁移过程中的形变和平衡位置,为囊泡在药物输运、化学反应和生理过程的应用提供可靠的计算依据.

然而也注意到,由于本文采用的模型在大雷诺数时收敛性不佳,导致本文计算的囊泡膜的模量和黏度变化区间,尤其是雷诺数大小受到了限制.如何进一步提高模型的收敛性和计算效率,以便更好地考虑更大参数范围内囊泡的惯性迁移规律,是未来工作的重点.