垂直振动下干湿颗粒样品的体积模量与耗散*

杜清馨 孙其诚 丁红胜 张国华 范彦丽 安飞飞

1) (北京科技大学物理系,北京 100083)

2) (清华大学,水沙科学与水利水电工程国家重点实验室,北京 100084)

研究了垂直振动条件下,干、湿玻璃珠样品的体积模量和相对耗散.实验发现: 1)在低饱和度下,干、湿玻璃珠样品的体积模量随压强幂律变化,与基于赫兹接触势的有效介质理论预言的1/3 幂律关系接近;加入少量液体会增加体积模量.同一压强和液体含量下,随着液体黏度的增大,体积模量随之增加.基于赫兹接触力学,提出了有效弹性网络模型来阐述湿玻璃珠样品体积模量的增加机制.2)干、湿玻璃珠样品的相对耗散随压强幂律降低,湿玻璃珠样品的相对耗散与液体黏度呈正比.3)随着应变幅值的增大,湿玻璃珠样品表现出类似干玻璃珠样品的软化行为,且液体黏度会抑制玻璃珠样品的软化行为.

1 引言

颗粒材料是由大量离散固体颗粒组成的复杂体系,其宏观力学性质是由颗粒间的相互作用决定的.目前,对于由球形颗粒组成的干颗粒材料体积模量的研究已经取得了一些共识.如基于赫兹接触势的有效介质理论[1-3]和实验[4,5]表明,低压强下球形颗粒体系的体积模量K随压强p呈幂律标度,K ∝p1/3.

对于湿颗粒材料,材料的宏观力学性质受颗粒骨架与液体相互作用的影响.近年来,人们对于湿颗粒材料力学性质的研究也取得了一些进展.Badetti 等[6]发现湿颗粒材料的力学性质在液体含量较低时由颗粒间的液桥决定,而在液体含量较高时则由液体通过颗粒间隙的流量决定.唐瀚玉等[7]和Fall 等[8]发现湿颗粒材料的刚度随着液体含量的增加,并非单调变化.但是,关于颗粒骨架-液体相互作用对颗粒材料力学性质影响的研究仍然是颗粒力学领域的研究热点.

目前,关于颗粒耗散机制的研究也取得了很大进展.研究表明,黏弹性颗粒材料的耗散机制主要来源于界面处的摩擦耗散、内部的黏性耗散以及颗粒尺度结构变化引起的耗散等.比如,Wang 和Zhu[9]发现干颗粒材料的能量耗散主要来源于摩擦耗散以及由力链结构微小变动引起的耗散;Brunet 等[10]发现干玻璃珠样品的耗散主要来源于线性黏性耗散和非线性摩擦耗散的相互作用,而湿玻璃珠样品中的耗散则主要源于线性黏性耗散.Kovalcinova 等[11]的模拟发现湿颗粒材料中毛细力引起的颗粒接触处的摩擦增强以及液桥的断裂和形成引起了能量耗散.湿颗粒材料中的能量耗散仍然是近年来研究的热点问题.

与传统固体和液体不同,颗粒材料中存在多种类型的亚稳态结构,如颗粒骨架、力链、液桥等.当施加足够大的剪切或振动时,这些结构失稳,整体上颗粒体系发生软化,也就是表现为从类固态到类液态的转变.目前,关于颗粒材料软化的研究大多都集中在干颗粒材料,Johnson 和Jia[12]的声速实验表明颗粒材料的软化效应是由颗粒接触处的摩擦非线性造成的.Reichhardt 等[13]模拟发现颗粒材料的软化与颗粒接触数的减少有关.Lemrich 等[2]模拟发现有摩擦玻璃珠材料的软化与接触点的断开和形成有关.近年来,人们开始研究湿颗粒材料的软化行为,如唐瀚玉等[7]研究湿颗粒材料的力学谱,发现湿颗粒材料也会发生与干颗粒类似的软化行为.Brum 等[14]实验发现湿颗粒材料模量的软化有两个连续的过程: 微观尺度上的接触滑移,导致模量减弱;宏观尺度上颗粒塑性重排伴随着模量显著降低.干颗粒材料的软化研究已经取得了一些进展,但是关于湿颗粒材料软化行为的研究还比较缺乏,有待进一步研究.

为了研究颗粒骨架-液体相互作用对颗粒材料动力学特性的影响,本文测量了垂直振动条件下,干、湿玻璃珠样品的体积模量和相对耗散,分析了压强对体积模量的影响,并采用基于赫兹接触势的有效介质理论予以解释;得到了湿玻璃珠样品的体积模量随着黏度的增加而增加,相对耗散均与压强呈负相关,以及在低压强下,相对耗散随黏度线性增加等规律.

2 实验装置和测量原理

实验装置如图1 所示.实验装置固定在大理石工作台下表面,以保证实验过程中样品室在振动台(ESS-050-120)冲击下不会向上移动.样品室为一个内径D=80.0 mm 的圆柱形不锈钢杯,其底部开一圆孔.在样品室底部放置一个激励活塞,活塞和杯体之间垫一圆环形橡胶圈,防止颗粒渗漏.粒径0.4—0.6 mm 的球形玻璃颗粒置于样品室底部活塞和顶部保压板之间,玻璃颗粒的填充高度为50 mm.保压板的上表面粘连一个压力传感器(YSV3041),通过旋转螺杆给颗粒施加静态压强p.在活塞和振动台之间刚性连接一个动态力传感器(502F020),实时测量振动台对活塞的作用力F(t)=F0sin(ωt+ϕF)(其中F0和ϕF分别为振动台对活塞作用力的振幅和初相).在激励活塞下表面粘连一个加速度传感器(YA22T),用于测量活塞的加速度a(t)=a0sin(ωt+ϕa)(其中a0和ϕa分别是加速度的振幅和初相),通过计算可进一步得到交变应变ε(t)=ε0sin(ωt+ϕε) (其中ε0和ϕε分别是应变的振幅和初相).由于实验中F(t)和a(t) 是同步测得的,数据处理使用的是应力和应变的位相差,因此,尽管不同初始条件的位移x(t)和应变ε(t)的初相不一样,对于后续数据处理并不影响.考虑到活塞具有一定的质量m,本文分别测量了相同条件下空载和加载时振动台对活塞的作用力F1(t),F2(t).假设空载与加载测量过程中活塞的加速度相同,则加载测量时颗粒对活塞的力F′(t)=F2(t)-F1(t),进一步得到活塞对颗粒施加的交变应力σ(t)=σ0sin(ωt+ϕσ)(其中σ0和ϕσ分别为活塞对颗粒施加应力的振幅和初相).

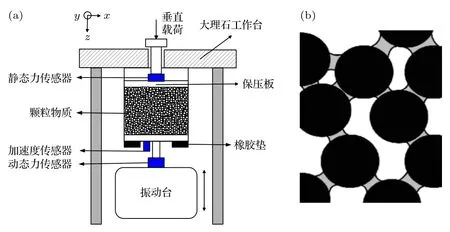
图1 (a)实验装置示意图;(b)湿颗粒体系中的液桥形态示意图Fig.1.(a) Schematic diagram of the experimental device;(b) pendular bridges in wet glass bead sample.

振动台和工作台均安装了防震橡胶垫,以减少环境的干扰.将上述传感器连接到高速数据采集卡上(ZD-4008),用Labview 程序同步控制振动台振动和数采卡采集数据,设置数采卡的采样频率为128 kHz,每组数据的采集时间为1 s.

一个外力循环中机械能的损耗为ΔW=,ϕ是应变落后于应力的相位差.外力对样品作的功是,在 1/4 循环中振动系统损失的机械能是 ΔW/4,因此振动系统最大储能为W=.类比固体内耗,定义颗粒体系的相对能耗为

体系的体积模量可利用测量的应力振幅σ0和应变振幅ε0得到

3 实验结果与讨论

颗粒系统是一个典型的非平衡系统.在没有外界干扰的情况下,系统会长期处于某种亚稳态构型,因此颗粒系统的力学性能取决于制备历史.为了消除历史效应的影响,本文采用以下方法来制备样品.具体过程如下: 1)将玻璃珠通过漏斗均匀地降落在样品池中,以保证落在样品池中的颗粒可以达到随机密堆的状态;2)拧动螺杆给样品表面施加一个预压力,然后给系统添加一个扰动,以1500 Hz 频率,0.3g的加速度垂直振动210 min,驱动样品重新排列和压实,使玻璃珠颗粒更加密实,密度达到一个较稳定的值.

为了减小压强变化过程中颗粒填料内部结构的重排,实验过程中通过卸载过程来改变样品的压强.具体卸载协议如下: 首先用上段所述的样品制备协议制备压强约30 kPa 的颗粒样品.然后,给样品施加一个频率f=300 Hz (远离共振峰以避免系统共振的影响)、位移幅值A=565 nm (位移幅值远小于颗粒直径)的交变微扰振动,在体系达到稳定(约300 s)后采集数据.对该信号进行频谱分析,频谱图如图2 所示.可以看出,不仅存在基波,还存在高次谐波,但是高次谐波幅值远小于基波幅值(二次谐波幅值是基波幅值的2%),因此将高次谐波的影响忽略.测量完成后,缓慢松动螺杆使颗粒样品表面压强降低,在固定体积下使颗粒样品充分松弛(约10 h) 以确保测量过程中颗粒样品表面的压强近似是一个常量(当连接在螺杆和活塞之间的静力传感器的压力波动范围小于压力值的5%时,压强可以近似看作一个常量).为了验证实验的可重复性,每个压力值重复测量7 次.重复上述过程,实现对不同压强下颗粒样品体积模量和相对耗散的测量.

图2 频率 f=300 Hz、位移幅值 A=565 nm 的正弦加速度信号(a)及其频谱图(b)Fig.2.(a) Sinusoidal acceleration signal with frequency f=300 Hz and displacement amplitude A=565 nm and(b) its spectrum diagram.

本文所用湿颗粒样品的制备协议如下: 首先,用旋转、搅拌方法使得硅油和玻璃珠颗粒均匀混合,从而制备自由表面的湿颗粒样品.然后,采用与干颗粒样品相同的制备和卸载协议制备不同压强下的湿颗粒样品.定义湿颗粒样品的液体含量w为液体质量与颗粒质量的比值,本文选用w=1 %的样品,以确保湿颗粒间的液桥形状为钟摆形(pendular bridge)[6].选用运动黏度为100—5000 cst(厘斯,1 cst=1 mm2/s)的硅油作为润湿液体.

3.1 体积模量随压强的变化

图3 给出了同一液体含量下,不同运动黏度νlig玻璃珠样品的体积模量K随压强p的变化.在每个压强下的7 次测量过程中加速度信号、动态力信号以及压强的轻微波动会对实验造成一定误差,每个压强下的体积模量的相对误差小于2%,相对耗散的相对误差小于4%.由图3 可以看出,不同运动黏度的玻璃珠样品的体积模量均随压强幂律增加,K ∝pa,幂指数a的值如表1 所列.根据赫兹接触势的有效介质理论[2],低压强下无摩擦球形颗粒样品的体积模量随压强的变化规律为K ∝p1/3(如图3 中的橙色虚线所示).本文测得的干玻璃珠样品体积模量随压强变化的幂指数(0.396)接近赫兹接触势的有效介质理论的理论值(1/3).另一方面,本文测得的湿玻璃珠样品的体积模量随压强变化的幂指数为 0.327—0.370,是比干玻璃珠样品的更接近基于赫兹接触势的有效介质理论的理论值,这是由于加入液体不仅增加了颗粒间的接触数,而且还会在颗粒间形成液桥,导致颗粒间的内聚力增加[6],从而使得接触增强,减少了颗粒间接触发生滑移的概率.需要指出的是,Griffiths 等[15]的实验也发现湿玻璃珠样品的体积模量随着压强的增加而幂律增加,且幂指数与基于赫兹接触势的有效介质理论的理论值更接近.结果表明,在本文的实验精度范围内,基于赫兹接触的有效介质理论对有摩擦低饱和度的玻璃珠样品同样适用.

图3 不同运动黏度 νlig 下,玻璃珠样品的体积模量K 随压强p 的变化(液体含量 w=1 %)Fig.3.Variation of bulk modulus K of glass bead samples with pressure p under different kinematic viscosity νlig (liquid content w=1 %).

表1 不同运动黏度下,玻璃珠样品体积模量和相对耗散随压强变化的幂指数Table 1.Power law exponents of bulk modulus and energy dissipation with pressure and kinematic viscosity.

为了分析湿玻璃珠样品的体积模量,本文引入一个有效弹性网络模型.假设湿玻璃珠样品可以看作由赫兹接触和液桥并联组成的有效弹性网络.根据赫兹接触力学,赫兹接触力FcH与法向位移δcH的关系为,接触刚度,即kn～.加入少量液体后,颗粒之间除了赫兹接触力外还存在液桥力.液桥力Fl等于表面张力引起的毛细力Fc与液体运动黏度引起的黏性力Fv的合力[16],即Fl=Fc+Fν,其中毛细力Fc为

式中R是颗粒半径,γ是液体的表面张力,θ为颗粒与液体的接触角,Vb为液桥体积,Dl是液桥的分离距离.注意,在本文中,液体体积保持不变,且不同黏度硅油的表面张力彼此接近(γ=21 mN/m±0.3 mN/m),因此可以认为本文中不同黏度的湿玻璃珠样品中的毛细力几乎相同.

黏性力Fv可以写成

液桥的接触刚度kl=.当给干玻璃珠样品施加载荷时,假设样品中所有的接触都是赫兹接触,干玻璃珠样品的体积模量为

其中,ncH是相邻两层玻璃珠之间的赫兹接触的平均数.对于湿玻璃珠样品,需要考虑并联的液桥接触网络,其体积模量为

其中,ncl是相邻两层玻璃珠之间的液桥接触的平均数.

当液体含量一定时,相邻两层玻璃珠之间的液桥接触的平均数ncl为固定值,且液桥的接触刚度kl随着压强的增大而增加[17],相邻两层玻璃珠之间颗粒的平均接触数随压力的增加及加入液体而增大[18].造成玻璃珠样品的体积模量随着压强的增加而增大,且湿玻璃珠样品的体积模量比干玻璃珠样品的高.Liu 等[19]基于Biot 理论获得的理论结果、Li 等[20]基于Gassmann 理论获得的理论结果,以及Fawad 等[21]的实验结果均表明少量液体能够有效增加颗粒材料的体积模量,与本文的结果定性符合.

Brunet 等[10]发现,液体可以通过润滑摩擦或引入黏性滑动等机制改变颗粒材料内部的接触网络,进而影响颗粒体系的模量.为分析运动黏度对湿玻璃珠样品体积模量K的影响,本文从图3 不同运动黏度湿颗粒的体积模量随压强变化的拟合曲线中提取了4 个压强下玻璃珠样品的体积模量(如图3 中垂直虚线所示),进一步得到不同压强下湿玻璃珠样品体积模量K随液体运动黏度νlig的变化,如图4 所示.可以看出,同一压强和液体含量下,湿玻璃珠样品的体积模量K随着运动黏度的增加而增大.根据有效弹性网络模型,湿玻璃珠样品的体积模量与接触刚度和相邻两层玻璃珠之间颗粒的平均接触数有关.实验中毛细力为定值,且液体体积不变,所以液桥力仅由与运动黏度有关的黏性力决定,向颗粒材料中添加高黏度液体会导致颗粒间形成的液桥力增大((4)式),且颗粒间的接触刚度也随之增加.另外实验中湿颗粒样品中相邻两层玻璃珠之间颗粒的平均接触数也为定值[17],从而造成湿玻璃珠样品的体积模量也随运动黏度的增加而增大((6)式).本文结果表明,在低饱和度下,湿玻璃珠样品体积模量的增加与运动黏度有关.

图4 不同压强 p 下,湿玻璃珠样品的体积模量K 随运动黏度 νlig 的变化(液体含量 w=1 %)Fig.4.Variation of bulk modulus K with kinematic viscosity νlig under different pressure p (liquid content w=1 %).

3.2 相对能耗随压强的变化

图5 给出了同一液体含量的不同液体运动黏度νlig下,干、湿玻璃珠样品的相对能耗 tanϕ随压强p的变化.由图5 可知,不同运动黏度下,相对耗散 tanϕ均随着压强p的增加幂律降低,tanϕ ∝pb,幂指数b的值如表1 所列.

本实验测得的干玻璃珠样品的相对能耗随着压强的增加幂律减小,这是由于体系内可能潜在滑动的接触数量随着压强的增加减小,使得由于颗粒滑移导致的相对能耗随着压强的增加而减少.干玻璃珠样品的相对耗散随压强的变化规律与Brunet等[10]干玻璃珠样品实验结果相同.

由图5 可以看出,同一压强下湿玻璃珠样品的相对能耗比干玻璃珠样品的更大.这是因为液体在玻璃珠颗粒之间形成液桥,使得湿玻璃珠样品中除了存在与接触数有关的滑移耗散外,还产生了由于液桥的断裂和形成所产生的相对能耗[11],从而导致湿玻璃珠样品的相对能耗比干玻璃珠样品的大.

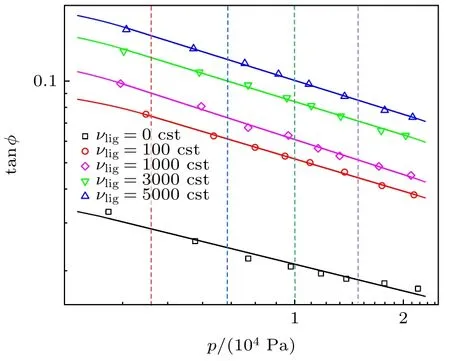
图5 不同运动黏度 νlig 下,玻璃珠样品相对能耗 tan ϕ 随压强 p 的变化(液体含量 w=1 %)Fig.5.Variation of relative energy dissipation tan ϕ with pressure p under different kinematic viscosity (liquid content w=1 %).

另外,由图5 还可以看出,湿玻璃珠样品的相对能耗随压强的增加幂律降低,与Tittmann 等[22]的实验结果相同.为分析液桥的断裂和形成所产生的相对能耗 tanϕlig随压强p的变化,假设湿玻璃珠样品中滑移耗散与干玻璃珠样品相同,本文从测得的湿玻璃珠样品的相对能耗随压强的拟合曲线中,选取7 个压强下的相对能耗值减去对应压强下未添加液体的干玻璃珠样品的相对能耗值,得到7 个压强下的 tanϕlig,如图6 所示.图6 中的实线为利用上述数据得到的液桥的断裂和形成所产生的相对能耗 tanϕlig随压强p变化的拟合曲线.由图6 可知,液桥的断裂和形成所产生的相对能耗 tanϕlig随压强p的增加而减少.这是由于压强的增加使颗粒移动的空间减小,导致液桥的断裂和形成的概率减小(由此产生的相对能耗也随着压强的增大而减小).湿颗粒样品内部颗粒间的滑移耗散以及液桥的断裂和形成所产生的相对能耗都随着压强的增加而减小,使得湿玻璃珠样品的相对能耗随压强的增加而降低.由图5 可知,液桥的断裂和形成所产生的相对能耗在湿玻璃珠样品的相对耗散中占主导地位.与Kovalcinova 等[11]在较低的外加压强下的模拟结果相同.本文结果表明在低饱和弱压缩系统中,相对耗散的主要来源是液桥的断裂和形成所产生的相对能耗.

图6 不同运动黏度 νlig 下,湿玻璃珠样品液桥的断裂和形成而产生的相对能耗 tan ϕlig 随压强 p 的变化(液体含量w=1%)Fig.6.Variation of relative energy dissipation by rupture and reformation of the capillary bridges tan ϕlig with pressure p under different kinematic viscosity νlig (liquid content w=1 %).

为分析运动黏度νlig对相对耗散 tanϕ的影响,从图5 中提取了4 个压强下湿玻璃珠样品的相对能耗(如图5 中垂直虚线所示),得到不同压强下湿玻璃珠样品的相对能耗 tanϕ随运动黏度νlig的变化,如图7 所示.可以看出,随着运动黏度νlig的增加,湿玻璃珠样品的相对能耗 tanϕ增加.这是因为液桥的断裂与形成所产生的相对能耗与运动黏度相关,相同压强和液体含量下,随着运动黏度的增加,加入液体所产生的液桥力呈线性增加,从而使得液桥的断裂与形成所产生的相对能耗呈线性增加.Brunet 等[10]指出加入液体会使颗粒之间产生黏性耗散 tanϕvis.当压强、液体体积都一定的情况下,黏性耗散与运动黏度呈正比: tanϕvis∝νlig.显然,在同一压强下,黏性耗散也随着运动黏度的增加而线性增大,与本文实验结果定性一致.需要指出的是,Aliasgari 等[23]的实验也发现,在同一压强下,颗粒材料的相对耗散随着运动黏度的增加而增大,也与本文结论定性一致.

图7 不同压强p 下,湿玻璃珠样品的相对能耗 tan ϕ 随运动黏度 νlig 的变化(液体含量 w=1 %)Fig.7.Variation of relative energy dissipation tan ϕ with kinematic viscosity νlig under different pressure p (liquid content w=1 %).

3.3 体积模量随应变的变化

定义玻璃珠样品的归一化体积模量为

其中K是存在振动时的体积模量,K0是初始稳态时的体积模量.本文测量了在固定压强(3000 kPa±400 kPa)下,ΔK/K0随应变幅值ε的变化,应变幅值的范围是从 1×10-6到 3×10-5.对于湿玻璃珠样品,选用运动黏度νlig=1000,5000,10000 cst 的硅油作为润湿液体.

同一压强下,不同黏度玻璃珠样品的归一化体积模量随应变幅值的变化曲线,如图8 所示.可以看出,干、湿玻璃珠样品存在一个近似的应变阈值εT(如图8 所示的垂直虚线对应的应变值),在低应变幅下,干、湿颗粒样品的归一化模量几乎不随应变幅值的增加而改变,当应变幅值超过某个值时样品的归一化模量开始明显减小,我们把这个值(即ΔK/K0开始小于0 的应变幅值)定义为应变阈值.低于该阈值,低幅振动基本上不改变颗粒材料的接触网络,颗粒材料表现为线性弹性介质,ΔK/K0不随振幅变化.高于应变阈值,颗粒材料发生软化,体系非线性变大,ΔK/K0降低.这是由于当应变幅值增大到某个临界幅值之上时,高幅振动导致颗粒发生滑动,使得内部出现大量颗粒重排,造成接触断裂,引起体积模量显著降低.Lemrich 等[2],Johnson 和Jia[12],以及Tong 等[24]利用声学方法研究颗粒体系的共振响应也得到与本文类似的结论.

为了探究运动黏度对玻璃珠样品归一化体积模量软化的影响.我们发现,νlig=0 时,εT=2.237×10-6;νlig=1000 cst 时,εT=2.502×10-6;νlig=5000 cst 时,εT=2.588×10-6;νlig=10000 cst 时,εT=2.921×10-6,如图8 中的4 个实心圆点所示.可以看出,湿玻璃珠样品的应变阈值比干玻璃珠样品的更大,且湿玻璃珠样品的应变阈值随着液体运动黏度的增加而增大.在湿玻璃珠样品中,液体会增加湿玻璃珠样品中颗粒的接触数量[18],使得湿玻璃珠样品比干玻璃珠样品更能抵抗外加振动,更不容易发生软化.在相同的输入振幅下,颗粒间接触断开的概率随着运动黏度的增加而减小[23].同时湿玻璃珠样品中存在与黏度成正比的液桥力,液桥力会增加颗粒间的内聚力,添加更高运动黏度的液体,使得颗粒接触更不容易断开[16],从而造成湿玻璃珠样品的应变阈值随着运动黏度的增加向高振幅方向移动.本文结果表明,在低压强下,与干玻璃珠样品相比,湿玻璃珠样品的构型更稳定,随着液体运动黏度的增加,玻璃珠样品的软化应变阈值增加.

图8 不同运动黏度 νlig 下,玻璃珠样品的归一化体积模量变化 ΔK/K0 随应变幅值 ε 的变化(液体含量 w=1 %).虚线对应近似的应变阈值,即当应变幅值低于阈值时,系统动态响应是线性的,ΔK/K0=0,与振幅无关;在高应变幅值下,ΔK/K0＜0,材料软化Fig.8.Variation of the normalized bulk modulus change ΔK/K0 with strain amplitude ε under different kinematic viscosity νlig (liquid content w=1 %).The dashed line indicates that there is an approximate strain threshold,when the strain amplitude is lower than the threshold value,the dynamic response of the system is linear,ΔK/K0=0,and independent of the amplitude.At high strain amplitude,ΔK/K0＜0,the system is softened.

4 结论

本文测量了垂直振动下,干、湿玻璃珠样品的体积模量和相对耗散随压强、运动黏度及应变幅值的变化,得到如下主要结论:

1)干玻璃珠样品的体积模量随压强呈幂律标度,K∝p0.396,幂指数 0.396 接近赫兹接触势的有效介质理论预测的1/3 幂律关系,表明赫兹接触势的有效介质理论在本文实验的压强范围内是有效的.不同运动黏度的湿玻璃珠样品的体积模量均随压强呈幂律增加,K∝pa(a≈0.327—0.370),幂指数比干玻璃珠样品更加接近赫兹接触势的有效介质理论的理论值(1/3),表明在本文的实验精度范围内,有摩擦低饱和玻璃珠样品同样适用赫兹接触势的有效介质理论.本文引入一个有效弹性网络模型,定性解释了湿玻璃珠样品体积模量的增加机制.同一压强下,湿玻璃珠样品体系的体积模量比干玻璃珠样品的更大,这是因为湿玻璃珠样品除了存在赫兹接触力外还存在液桥力.少量液体的加入会增加颗粒间的接触数,减缓颗粒间的相互运动,从而提高了颗粒体系力学性能的稳定性.考虑到湿玻璃珠样品的体积模量与接触刚度和接触数有关,而实验中湿玻璃珠样品毛细力和接触数为定值,且黏性力随着运动黏度的增加而增大,使得接触刚度也随之增大,最终导致湿玻璃珠样品的体积模量随着运动黏度的增加而增加.

2)低压强范围内,不同黏度的玻璃珠样品的相对耗散随压强的增加幂律减小,tanϕ∝pb,b≈-0.429—-0.327.这是由于颗粒样品中滑移耗散以及由于液桥的断裂和形成而产生的相对耗散均随着压强的增加而减小.同一压强下,湿玻璃珠样品的相对耗散随着运动黏度的增加而增大,这是由于液桥的断裂和形成而产生的相对耗散在湿颗粒样品的相对耗散中占主导地位,且液桥的断裂和形成而产生的相对耗散与运动黏度成正比关系.

3)干、湿玻璃珠样品随着应变幅值的增加会出现软化行为,即低应变幅值下,振幅对体积模量几乎没有影响,颗粒材料表现为线性弹性介质;当应变幅值超过阈值,颗粒发生滑移,使得系统内部出现大量颗粒重排,造成系统的体积模量开始降低.应变阈值随着运动黏度的增加而增大,这是由于湿颗粒间存在与黏度成正比的液桥力,液桥力会增加颗粒间的内聚力,使得颗粒接触更不容易断开.