气液两相射流破岩流场数值模拟
2022-09-30占凯张思唐伟程荫徐龙宇
占凯 , 张思*, 唐伟, 程荫, 徐龙宇
(1.长江大学机械工程学院, 荆州 434023; 2.长江大学机械结构强度与振动研究所, 荆州 434023)
高压射流破岩技术已被广泛应用于地下工程、煤炭石油钻井、瓦斯抽放以及隧道掘进等工程领域,涉及流体力学、岩石破碎学、射流动力学以及流固耦合的等多种学科,研究难度极大。目前,射流破岩技术遇到的问题越来越多,设备成本居高不下,高压力设备带来的严重安全隐患,随着井深的增加,地应力变高,破岩效率极度降低,传统水射流水资源消耗巨大,有违绿色环保的发展理念。为解决以上问题,开展射流破岩技术方面的研究是非常有必要的。
高压水射流具有能量传递集中、无污染、无磨损以及工作介质简单易获取等优点,设备自动化程度高,体积小,便于操作和控制。倪红坚等[1]建立了高压水射流动载和静载两个不同阶段的岩石损伤模型,模拟了岩石损伤的整个过程,将岩石损伤场耦合到无损伤应力场,所得结果与实验相符。梁运培[2]基于应力波在岩石介质中的传播方程,建立了水射流冲击动载荷下的力学模型,得到了岩体中的应力场随时间变化规律。尽管高压水射流的优势极为明显,但想要提高其射流性能,必须使用更高压力的设备,设备制造成本也越发增高,超高压设备带来的安全隐患也更加严重。为了解决这些问题,一系列高压射流相继问世。卢义玉等[3]对高压空化水射流的岩石破碎能力进行了一系列实验,探究了空蚀效果与泵压、围压的变化关系;席宝滨等[4]利用高围压射流破岩模拟设备,进行了风琴管空化射流模拟实验,实验结果显示,风琴管空化射流可以有效提高钻井速度。空化射流对喷嘴的要求极高,无法定量控制气相的生成,并且受温度、岩层孔隙率的影响严重,在淹没条件下,冲击靶距更是极小。而脉冲射流和自激振荡射流刚好在一定程度上弥补了这方便的不足,李晓红等[5]开展了振荡射流在低透气性煤层中动力效应的实验研究,结果显示,自激振荡射流能有效增加煤层透气性。因为自激振荡射流的固有频率不同,压力输出响应也不同,而固有频率又主要是由喷嘴形状决定,所以当岩层硬度发生变化时,射流的固有频率等参数调整极为不便,而设备能耗大,液压损耗也大。
针对以上不足,直接将一定体积分数的气相引入纯水射流,形成气液两相射流。由于空化射流空化生成的气相不易控制,而气液两相流是将定量、可控的压缩气体混入高压水射流中,提高射流冲蚀和破碎性能。同时,高压的气相能够对射流起保护作用,相比介质单一的射流具有更好的稳定性[6]。因此,现将开展气液两相流在破岩方面的研究,对气液两相射流的流场进行仿真分析,研究其射流特性,以及射流参数对破岩效果的影响规律,推动气液两相射流破岩技术的发展。
1 喷嘴结构
1.1 气液两相射流工作原理及喷嘴结构
入口通入混合好的高压液相、气相,两相混合均匀,气相体积分数以及入口压力可任意控制。喷嘴为风琴管空化喷嘴,射流在喷嘴处会形成局部低压区和负压区,此区域内发生空化效应,但是空化量不大,产生的气泡量与射流本身存在的气泡量相比差距悬殊,因此本研究忽略喷嘴产生的空化效应。射流自喷嘴喷射出时,气泡由于内外压差的驱动开始膨胀,膨胀到一定程度,又会受制于表面张力的作用,气泡开始逐渐收缩,最后发生溃灭[7]。气泡的溃灭并不是连续的,具有脉动冲击特性,而溃灭产生的溃灭微射流速度猛增,对流场流速提高有着巨大作用,同时射流可以看作被气泡分隔开的一段段小水柱,对靶面的冲击也具有脉动特性[7]。在整个过程中,气泡的膨胀到溃灭需经历一定时间,也就是存在一个时间点,大部分气泡会集中发生溃灭,产生巨大能量。气液两相射流喷嘴结构示意图如图1所示,结构参数如表1所示。

图1 喷嘴结构示意图Fig.1 Structural diagram of nozzle

表1 喷嘴结构尺寸Table 1 Nozzle structure dimensions
1.2 性能评价指标
射流冲击压力虽然不能等同于岩石的破碎性能,但它仍是衡量岩石破碎性能的一个重要参数[8]。而真正决定岩石破碎性能的是射流冲击动压,与速度的平方成正比,因此将靶面压力和流场速度作为衡量射流破岩性能的两个指标。
被气相分隔开的液柱在冲击岩体表面时形成局部水锤压力,这种水锤压力对岩体表面具有很强的冲击破坏效果,持续时间极短,并且随着速度的增大而增大,在岩体表面产生的局部水锤压力表达式[9-10]为
(1)
式(1)中:v为射流速度,m/s;ρw、ρs分别为液相和岩体的密度,kg/m3;cw、cs为液相和岩体的声速,m/s。一段液柱冲击过后又会有新的液柱再次冲击,每次冲击都会在靶面上会产生水锤压力,使射流具有脉动特性,在靶面产生巨大的脉动冲击力。同时,射流中气泡溃灭产生的微射流也具有连续性和脉动特征,对岩体表面造成脉动冲蚀破坏。
均相流两相混合均匀、各向同性,考虑两相之间存在扰动产生的激波效应。因气液两相属于混合相,与单一的液相介质相比,其扰动波传播速度较小[11]。空气动力学明确表示,当下游子波波速大于上游子波波速,上下游子波会压缩形成正激波,其波阵面为垂直于流动方向的压力阶跃面[11]。由普朗特激波关系可推导出气液两相射流在激波前后的冲击动压关系表达式[5]为
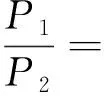
(2)
式(2)中:P1、P2为激波前后冲击动压,MPa,φ、α、ρl、ρg、a′分别为速度系数、气相体积分数、液相密度、气相密度、气液两相射流的湍流系数;cg为气相声速,m/s;w、R、T、K分别为容积比、气体常数、截面平均温度、均相流绝热指数。从式(2)得知:气液两相射流冲击动压与喷距S、初始压力P0、气相体积分数α、喷嘴直径D0成函数关系。因此本文中将选取喷距、初始压力以及气相体积分数3个因素对气液两相射流破岩性能参数的影响规律。
2 数值模拟
根据对气液两相流实际情况的检测与鉴定,气液两相流任意横截面上的气液分布是均匀的,并且同一横截面上的水滴、气泡大小基本相同[8]。因此,可考虑将气液两相射流看作均相流动模型,两相介质的流动呈完全混合状态,并假设两相介质具有完全相等的速度,无能量交换,充分考虑气液两相介质之间的相互作用力[8]。所以将采用Mixture模型进行数值模拟,该模型是一种简化的欧拉多相流模型,适用于两相速度相同的均相流动模型,重点考虑气液两相射流流场分布情况,简化单一气泡的相界面和瞬态动力学问题,符合本文模拟需求。同时,设置水为液相,空气为气相,以及各相体积分数。
2.1 物理建模及网格划分
选取风琴管喷嘴作为本研究的模拟对象,建立气液两相射流物理模型。在纯水射流中引入高压气相,其气体体积分数远大于空化产生的气相,并且可以定量控制射流中的气相体积分数,因此本仿真暂未考虑空化产生的气相。本文研究的是气液两相射流的破岩性能,所以设置岩体靶面为喷射壁面,设置喷射外流场圆柱面为出口;同时,简化管道长度为100 mm,设置管道直径为20 mm,喷嘴直径为4 mm。对气液两相射流流体域进行物理建模和网格划分,流体内部轴心区域网格作加密处理,提高计算精度,总网格数为185 989。如图2所示。

图2 网格模型Fig.2 Grid model
2.2 控制方程
以不可压缩的液态水为主相、空气为第二相的混合流体流动满足连续性方程、动量方程、k-ε湍流模型[12-15]。
(1)连续性方程:

(3)
式(3)中:ρ为混合流体密度;u为速度矢量;t为时间。
(2)动量方程:


(4)
式(4)中:p为压力;μ为流体黏度;g为重力体积力;Fs为外部体积力。
(3)采用k-ε湍流模型,其中k、ε的方程为

(5)
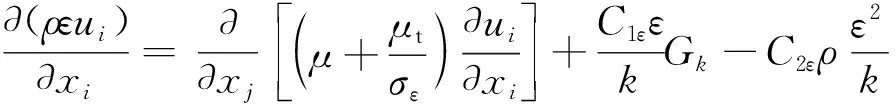
(6)
式中:x为空间坐标;k为湍动能;ε为耗散率;σk为k的普朗特数;Gk为平均速度梯度引起的湍动能的产生项;μt=Cμρk2/ε,为湍动黏度;C1ε、C2ε、Cμ以及σε为模型经验常数。
2.3 网格无关性验证
为验证仿真准确性,特作此网格无关性分析,探究了评价性能指标随网格数增加出现的变化趋势,结果如图3所示,可以明显看出,当网格数为82 074以上时,流场最大轴向速度稳定在288 m/s,

图3 最大轴向速度和驻点压力随网格数变化趋势Fig.3 Variation trend of maximum axial velocity and stagnation point pressure with grid number
网格数继续增加时,最大轴向速度保持不变,因此可以认为当网格数达到82 074时,流场最大速度基本准确。而驻点压力在网格数为115 278以下时波动较大,受网格数量影响严重,当网格数达到185 989时,驻点压力逐渐趋于稳定。在既确保计算结果的准确性,又尽量减少计算成本的前提下,综合考虑,此仿真将控制网格数在185 989以上。
3 模拟结果
3.1 气液两相射流相比纯水射流
在30 MPa入口压力下,纯水射流的最大轴向速度为241 m/s,如图4所示;气相体积分数为30%的气液两相射流的最大轴向速度为288 m/s,如图5所示;比纯水射流提高大约19%。在喷嘴段,射流中本身存在的气泡与液相相互挤压,导致射流横截面减小,射流流速相应增加;当气液两相射流自喷嘴喷出时,由于压差驱动和气泡表面张力的影响,射流中存在的气泡会不断溃灭,爆发出巨大冲击力推动微液滴流动,形成大量高速微射流,大量高速微射流的叠加引起流场剧烈变化,对流场流速的增长起促进作用。

图4 纯水射流速度场和气相体积分数Fig.4 Velocity field and gas volume fraction of pure water jet

图5 气液两相射流速度场和气相体积分数Fig.5 Velocity field and gas volume fraction of gas-liquid two-phase jet
3.2 气液两相射流流场分析
3.2.1 速度场
气液两相射流的速度场如图6所示在管道内流场段,流场流速几乎不变,接近10 m/s。当流体进入收缩段,管道直径变小,流体压能开始转换为动能,速度逐渐缓慢增加,变化不是非常明显;当射流进入喷嘴段,流体管道直径进一步缩小,此时压能几乎全部转换为动能,流场速度迅速升高,最大轴向速度达到288 m/s,开始出现“等速核”。在此过程中,流场中存在的气泡在喷嘴外流场处发生溃灭,形成溃灭射流,对流场流速的进一步增长起到了关键性作用。当射流不断冲出,直到接触靶面时,由于靶面的阻挡,流场速度开始断崖式衰减,此时射流动能几乎全部转换为压能,速度衰减至0,与伯努利原理相一致。
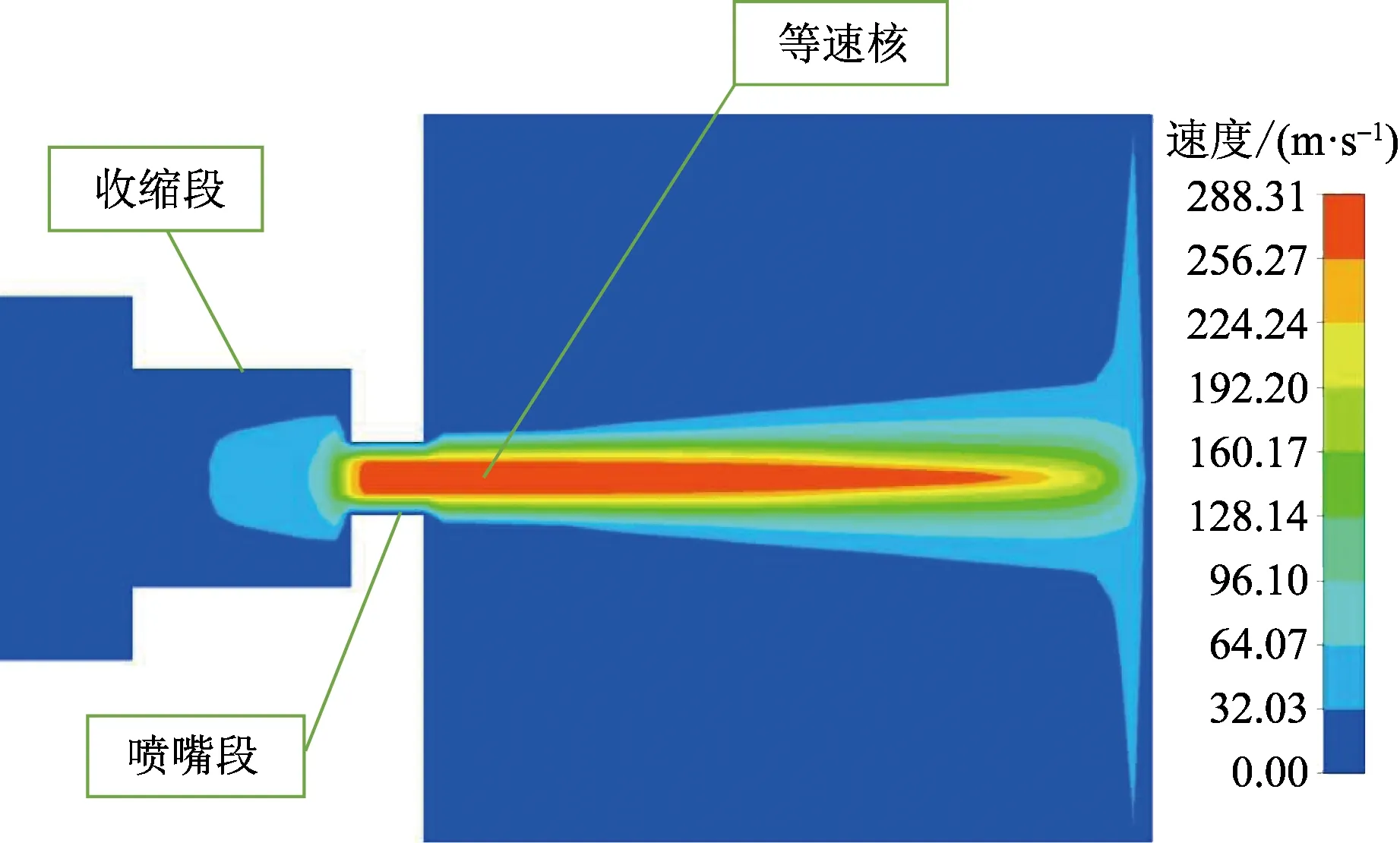
图6 气液两相射流速度场云图Fig.6 Cloud diagram of gas-liquid two-phase jet velocity field
3.2.2 压力场
气液两相射流流场压力分布如图7所示,流场内流管道区域内压力几乎不变,并接近入口压力,进入收缩段时,压力也几乎不变;但是,当射流靠近喷嘴段时,压能开始转换为动能,压力迅速降低;随着流体进入外流场,气泡开始发生溃灭,但外流场与出口相连,压力接近大气压;当射流开始冲击靶面时,流体动能几乎全部转化为压能,靶面压力急剧上升,气泡的溃灭也会加速微射流的运动,提高射流动能,在冲击靶面时转化为压能,提高靶面压力。靶面压力如图8所示,驻点压力最大,可达13.5 MPa,周围压力沿径向逐渐降低。
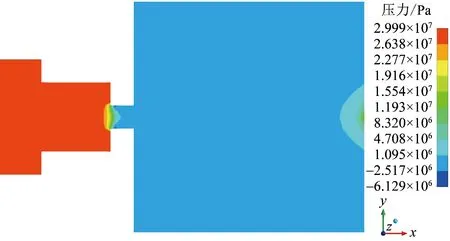
图7 气液两相射流压力云图Fig.7 Pressure nephogram of gas-liquid two-phase jet
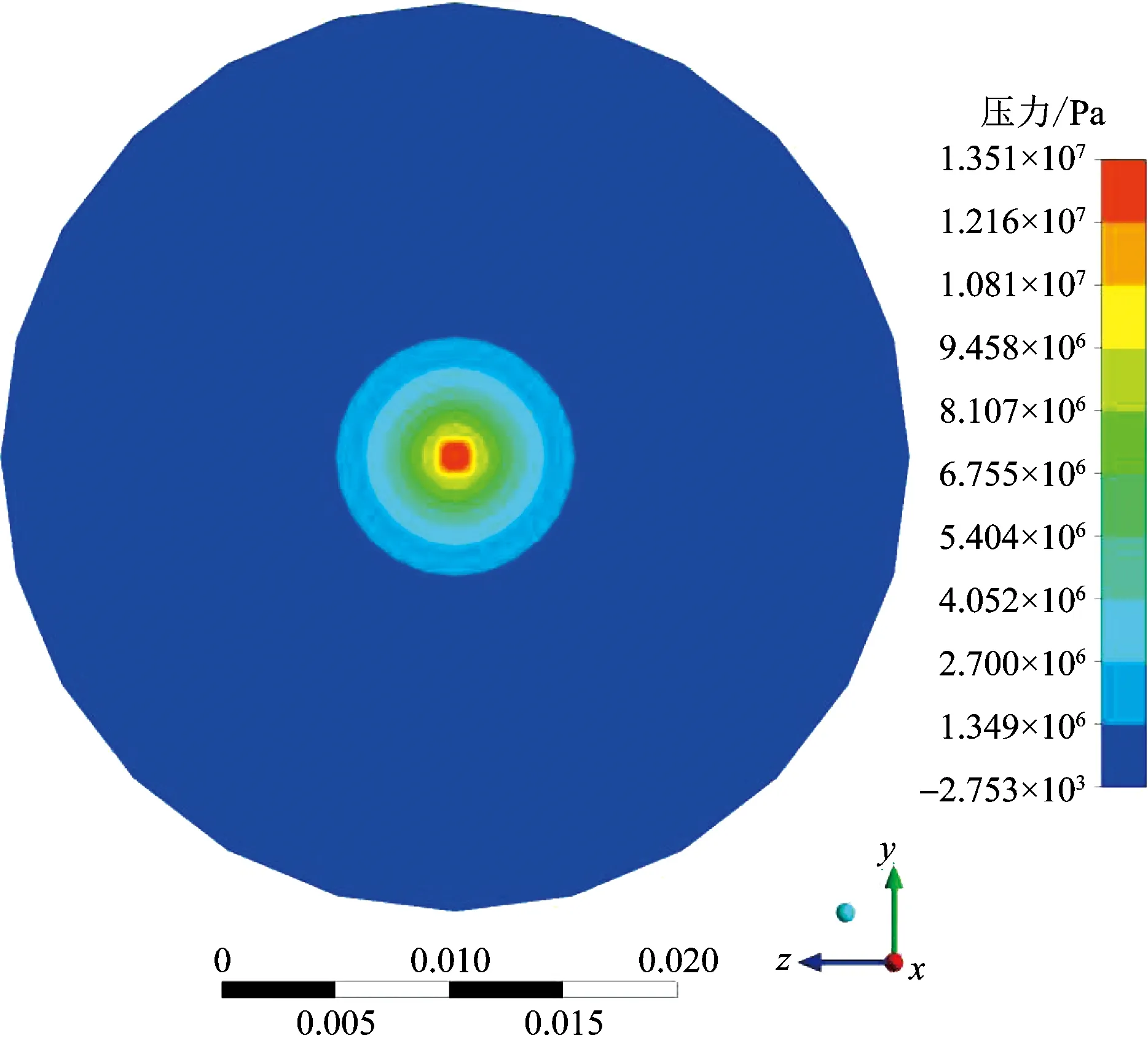
图8 喷射靶面压力云图Fig.8 Pressure nephogram of jet target surface
4 影响因素分析
4.1 气相体积分数影响分析
入射压力为30 MPa,并且其他参数保持不变时,气液两相射流流场轴向速度随气相体积分数变化规律如图9所示,管道段压力接近入射压力,射流速度小,射流进入收缩段时,速度开始逐渐上升,当射流进入喷嘴段时,压力能开始转化为动能,速度陡增,并形成一段等速核,随后射流冲击在靶面上,速度衰减至0。随着气相体积分数的增大,射流在喷射流场的速度不断升高。气相体积分数加大,流场气泡增多,喷嘴段横截面积减小,对射流轴向速度的升高也起着关键性作用。而随着气相体积分数的增加,射流流场其他位置均无明显变化,等速核长度也基本不变。
在喷距为40 mm时,气液两相射流喷射靶面压力随气相体积分数变化如图10所示,气相体积分数增大,靶面驻点压力略有减小。随气相体积分数的增加,射流中的气相在喷嘴处开始向外逐渐扩散,导致射流不集中,对靶面冲击减小,靶面压力降低。

图9 不同气相体积分数下的流场速度变化规律Fig.9 Variation law of flow field velocity under different gas phase volume fraction

图10 不同体积分数下的靶面压力变化规律Fig.10 Variation law of target surface pressure under different volume fraction
综上,随气相体积分数增大,流场最大轴向速度和靶面驻点压力的变化规律如图11所示,流场最大速度不断增加,但增加幅度略有下降;而靶面驻点压力随气相体积分数增加而缓慢下降,故其破岩性能应结合实际情况而定。

图11 流场最大轴向速度和驻点压力 随气相体积分数的变化规律Fig.11 Variation law of maximum axial velocity and stagnation point pressure of flow field with gas phase volume fraction
4.2 入射压力影响分析
保持气相体积分数为30%,喷距为40 mm不变,在不同入射压力下,流场速度变化规律如图12所示,随入射压力增加,管道段流场流速稍有提升,在喷嘴段开始呈断崖式上升,等速核长度略有增大。入射压力越大,射流能量越高,在喷嘴处由压能转化成的动能也越大,当入射压力达到40 MPa时,流场最大轴向速度提升至333 m/s,相比10 MPa入射压力下的最大轴向速度提高超过100%。
随入射压力的增加,流场最大轴向速度和靶面驻点压力变化规律如图13所示,流场最大轴向速度虽然在不断增大,但增大幅度却呈下降趋势,由入射压力增加带来的增速收益也逐渐减小;而靶面驻点压力也同样不断增长,且增长速度较快。若不考虑压力成本,尽可能增大入射压力,以提高气液两相射流的最大轴向速度和驻点压力,获得更好射流破岩性能。
4.3 喷距影响分析
当气相体积分数为30%、入射压力为30 MPa时,在不同喷距下,靶面压力分布曲线如图14所示,射流由喷嘴射出,在接触靶面时,射流动能全部转化为压能,射流中心部位较为集中,而表层则向外扩散,因此靶面驻点压力最高,周围压力沿径向方向迅速衰减,接近出口处压力为0。靶面驻点压力随喷距变化规律如图15所示,喷距为20 mm时,靶面驻点压力可达28.1 MPa,此时射流刚出喷嘴,表层射流向外扩散较少,射流撞击靶面后产生回流对后续射流冲击造成巨大阻碍,驻点压力虽高,但射流能量释放不全,无法达到最佳破岩性能;当喷距继续增加至30 mm时,射流向外扩散剧烈,能量损失较多,靶面驻点压力大幅度下滑,当喷距继续增加到35 mm时,靶面驻点压力又上升至26 MPa,这是因为射流中存在的高压气泡发生溃灭是需要一定的发育时间,当喷距为35 mm时,射流中的大部分气泡在与靶面相接触时刚好发生溃灭,产生的脉动冲击和溃灭微射流使靶面压力陡增,因此靶面驻点压力也随之增高;当喷距继续增加至40 mm时,大部分气泡已完成溃灭,靶面压力仅由动能转化,同时射流扩散进一步加重,能量损失严重,驻点压力迅速衰减。故在靶距为35 mm时,射流较为集中,靶面压力高,故破岩性能良好。

图12 不同入射压力下流场轴向速度变化规律Fig.12 Variation law of axial velocity of flow field under different incident pressure

图13 流场最大轴向速度和驻点压力 随入射压力变化规律Fig.13 Variation of maximum axial velocity and stagnation pressure of flow field with incident pressure

图14 不同喷距下的靶面压力分布曲线Fig.14 Pressure distribution curve of target surface under different spray distance

图15 靶面驻点压力随喷距变化规律Fig.15 Variation law of stagnation point pressure on target surface with jet distance
5 结论
针对风琴管喷嘴,通过数值仿真对气液两相射流的射流特性进行了详细分析,并探究了气相体积分数、入射压力及喷距3个因素对气液两相射流破岩性能参数的影响规律,得出以下结论。
(1)入射压力为30 MPa,气相体积分数为30%的气液两相射流最大轴向速度为288 m/s,相比纯水射流提高19%,高压气相的引入使得射流中的气、液两相相互挤压,射流在喷嘴处的横截面积减小,进一步导致气液两相射流速度增加。
(2)气液两相射流在管道段压力接近入射压力,射流能量存在形式以压力能为主,速度较小;当射流进入收缩段时,压力能开始转化为动能,速度开始增加;射流继续进入喷嘴段时,压力能几乎全部转化为动能,速度达到最大;最后射流冲击靶面时,射流动能转化为压力能,此时靶面压力升高,而速度衰减至0。
(3)随入射压力的增加,气液两相射流的最大轴向速度和驻点压力均不断上升,若不计压力成本,可尽量增大入射压力,使射流最大轴向速度和驻点压力进一步提高。
(4)随喷距增加,射流能量损失严重,靶面驻点压力急剧下降,当喷距为35 mm时,由于气泡的溃灭对靶面造成脉动冲击,靶面驻点压力回升到26 MPa,此时射流较为集中,靶面冲击压力大,破岩性能良好。
