多维度动态融合建模下4D飞行路径优化

2022-09-30李夏张飞桥严皓马昕

科学技术与工程 2022年23期

李夏，张飞桥，严皓，马昕

(中国民用航空飞行学院空中交通管理学院, 广汉 618307)

随着计算机各类功能的强化和元学习算法的推广，民用客机的运行控制对航迹预测日渐重视[1]，愈发依靠运行参数、空域数据和时间进程，对空域内的航空器数量、空间位置和空中交通管制态势进行分析和评价，由此设计4D飞机路径，推导出目标时间段内的运行情况前瞻结论，实现提升飞行安全和运行效率的目的[2]。4D飞行路径研究的核心内容是运行数据的采集提炼、综合分析和计算评价，且数据精细化程度要求较高[3]，其数字化体现在各类运行参数的预先处理和特征分析[4]，智能化体现在航空数据评价结论的科学使用[5]，对航班进、出港预计时间，飞机飞行各阶段空间相对位置关系[6]，即将可能面临的外部干扰与预期燃油消耗量[7]，飞行各阶段航空器性能与运行环境的适应性等，这些都是飞行任务能否按计划实施的重要影响因素，也是飞行路径规划与管理的基本参数[8]。

4D飞行路径规划现阶段研究主要集中在以下几个领域。首先是混合空域内联合运行研究，因智能物流技术的兴起和发展，以大型固定翼无人机为载体的航空物流逐步由实验转变为试运行，受机场数量、民用空域范围等诸多条件不足的限制，民航客机和大型无人机的运行矛盾较为突出[9]。在此背景下，张军峰等[10]对4D飞行路径规划的基本模型、算法进行了概念描述和归类；吕开妮等[11]开展了水平航迹的预测，提出了动态时间规整方法；刘杰等[12]在此基础上，搭建了无人机速度剖面模型，对进场时间管理提供了参考。但该方向的研究主要集中在无人机性能的模型建立，对民航客机的分析和评价缺少支撑[13]。其次为空域规划方法的创新，王宁等[14]提出了基于点融合规划4D飞行路径规划的方法，大幅提升终端区航班运行效率，但由于可适用点融合技术设计的机场和空域需具有流量较大、管制扇区较丰富的特点，且该技术仅可在进场飞行阶段提供计算，缺少了飞行各阶段评价的全面性。第三类是冲突评价模型的研究，丁松滨等[15]通过建立航空器冲突预警指示函数，可实现短时间内的4D飞行路径预测结论可靠性分析，但该类研究的时间维度考虑欠全面，预测时间推进较短，不适用于仪表飞行全过程。综上所述，现阶段研究成果为4D飞行路径预测建立了理论基础，具有一定借鉴意义，为顺应民航智慧空管发展趋势，建立飞行全过程评价策略，实现航空信息精准利用，面向多维度考虑下的4D飞行路径优化研究还存在可深入研究的空间。

1 问题描述

4D飞行路径规划是基于航空器传统三维航迹，即经度、纬度和高度的基础上，融入时间维度开展飞行路径规划[16]。由于其建立在航空信息数字化基础之上，则需要面向水平航迹进行规整和聚类，利用垂直剖面、速度剖面和高度剖面开展模型设计，从而实现对空间位置点精准预测[17]。另外，由于历史雷达航迹存在空间重叠和飞行趋势相似性的问题，在大范围空间路径识别和飞行环境衡量等问题上缺乏可靠的数学描述[18]，以及评价过程因数据类型欠丰富和特征不全面，导致4D飞行路径计算结果无法对实际飞行正常性提供支撑[19]。

为解决上述问题，使用层次聚类优化动态时间规整算法，面向垂直剖面、各飞行阶段速度剖面、高度剖面综合设计评价模型，实现多数据归类和特征分析，将进场航段各航路点飞行参数和空间位置数据作为采集对象，通过各剖面评价模型获取偏差值，结合国际民用航空组织(International Civil Aviation Organization，ICAO)在飞行安全评价中对缓冲值(buffer value，BV)的设定，形成4D飞行路径优化数据，实现基于4D飞行航迹规划的空间位置点预测和路径生成。

2 模型建立

由于历史飞行、导航、轨迹等数据具有体量大、数据质量可靠性低、呈现方式存在区别等特性[20]，而且飞行轨迹因导航精度和运行环境的因素，存在收敛处理和偏差修正的需求，以规范其数学描述。根据数据分类进行预处理，利用基于层次聚类的动态时间算法(hierarchical clustering dynamic time warping，HCDT)、动态空间算法(dynamic spatial warping，DSW)、高度剖面优化算法(height profile optimization，HPO)，分别对各飞行阶段下数据进行分析和处理，利用仿真实验获得飞行轨迹和时间维度结论，经计划到达时间tPTA与预计到达时间tETA阈值比较，实现基于4D飞行路径动态规整算法(4D dynamic warping，4DDW)构建的飞行路径预测，4DDW规划流程结构图，如图1所示。

2.1 水平飞行路径规划

通常情况下，整体空间内存在多个历史雷达航迹，使用基于层次聚类的动态时间算法(hierarchical clustering dynamic time warping，HCDT)可实现精确计算和特征统一[21]，主要依据有两点：①初始阶段历史轨迹数据类别较多，精确性较低，且随计算量增加将出现误差积累，导致计算结果失真，通过聚类优化的引入，可将导致误差积累的因素进行分类，筛选获得主要影响因素，为后续精准计算提供支撑；②因飞行速度不统一，飞行路径距离或范围不同，在时间轴上存在轨迹数据无法收敛，导致计算范围不具有典型性，通过特征筛选和HCDT模型建立，将初始阶段数据放在一个空间内进行比较，考虑其相似性，再将航迹视为时间序列并全局调整，实现时间序列长度统一，开展最优规整的比较，避免距离缺陷。

假设飞行路径1为X，飞行路径2为Y，由于研究空域范围内的飞行路径具有多样化、复杂性特征，为获取X与Y的规整路径最优值，则有

W=w1,w2,…,wk

(1)

式(1)中：W为最优规整路径，wk=(i,j)，数据越小表示飞行路径相似性越高。例如，在第k条飞行路径上用i和j表示其相似点。

如若存在相邻飞行路径长度为|X|和|Y|，则有

max(|X|,|Y|)≤k≤|X|+|Y|

(2)

式(2)中：K为相邻序列拉抻长度情况，如图2所示。

为保证相邻飞行路径1和2在空间数据中不重复，则规整路径需从w1=(1,1)起至wk=(|X|,|Y|)结束，并满足规整路径wk=(i,j)中的i和j单调递增，则有

图1 4DDW规划流程Fig.1 4DDW planning process

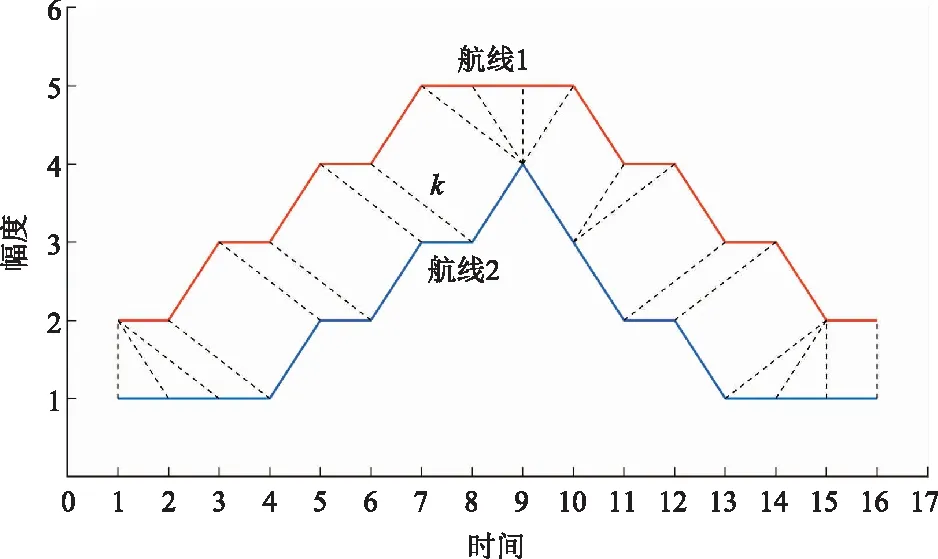
图2 动态时间规整Fig.2 Dynamic time warping

wk=(i,j),wk+1=(i′,j′)，i≤i′≤i+1,

j≤j′≤j+1

(3)

如若路径已存在wn=(i,j)，n=k，根据规整路径基本原理，则(i+1,j)，(i,j+1)，(i+1,j+1)三式中，下一阶段计算必选择其一进行。那么对于规整距离D(i,j)，存在

D(i,j)=Dist(i,j)+min{D(i-1,j),

D(i,j-1),D(i-1,j-1)}

(4)

式(4)中：Dist(i,j)表示相邻飞行路径间i和j的距离；D(i,j)表示相似性衡量值，用于处理飞行路径1在i之前的各个点，以及飞行路径2在j之前各个点。

通过上述模型建立，可获得规整路径距离D(|X|,|Y|)，D越小则相邻飞行路径相似性越高，在水平方向上完成对飞行轨迹精准性和特征筛选问题上的处理。

2.2 标称速度剖面设计

在速度剖面模型设计时，考虑了进场阶段飞行路径上各航空器机型和飞行性能，使用动态空间算法(dynamic spatial warping，DSW)并通过多个历史雷达轨迹，建立速度剖面模型P，公式为

P={p1,p2,…,pn}

(5)

式(5)中：pi为第i架航空器在飞行中的速度剖面。整理P集合获平均速度剖面，即为标称速度剖面psta，表示数据集合中的均值，且满足标称速度剖面psta∈P，则有

(6)

式(6)中：DSW(pi,pj)为动态空间距离，j可取任意值。

为提高航空器标称速度剖面的精度可靠性，需要求所收集数据在时间序列上长度一致，通过序列相似性对比，通过增加采样次数可提升数据长度一致性，从而实现对不同长度的时间序列进行有效比较。

设两个速度剖面为

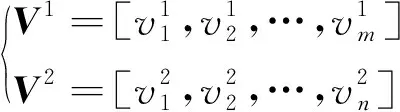
(7)

设A为速度剖面矩阵，开展数据对比，则有

(8)

通过计算临近速度剖面可获得弯曲路径，用W=(w1,w2,…,wk)表示，弯曲路径需要满足连续性、单调性和边界条件，则有

(9)

DSW算法在极限路径分析时具有保守性，适宜在飞行安全设计中应用，通过设置速度v1和速度v2间最小总距离，结合速度剖面矩阵，则存在

D(i,j)=a(i,j)+min{D(i-1,j),

D(i,j-1),D(i-1,j-1)}

(10)

(11)

为进一步提升计算结果有效性，需逐一使用速度剖面进行DSW距离计算并且引入缓冲值BV概念，实现对各速度剖面偏差值的处理，以最小偏差值速度剖面构成标称速度剖面，则存在

xi=BV+

(12)

2.3 高度剖面设计

在机场终端区飞行程序的仪表进近阶段，连续下降运行(continuous descent operations，CDO)作为一个新颖的技术正在由ICAO进行推广，CDO综合考虑平飞段和最短下降段对提升空域使用率的影响，可有效改善运行标准，提升着陆阶段的安全保障，则高度剖面模型采用CDO概念并进行设计。

根据CDO下降阶段投影到地面距离最短的特性，建立高度剖面优化算法(height profile optimization,HPO)模型，即

(13)

根据各下降阶段高度对控制障碍物的约束特征，建立约束条件函数，即

Hon≥An+MOCn

(14)

由于航空器的着陆阶段分为多个进近阶段，且每个进近阶段的最佳下降梯度要求各不相同，建立下降梯度限制函数为

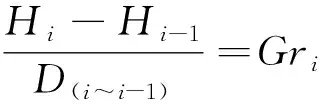
(15)

若此航段取最佳下降梯度且无关键障碍物限制，则

Di=D(i～i-1)=(Hi-Hi-1)/Gri

(16)

式中：Di表示第i个航段投影在地面的距离；Hon表示第n个障碍物处在航段的飞行高度；An表示第n个障碍物的高度；MOCn表示第n个障碍物所在地的最小超障余度(minimum obstacle clearance，MOC)；i表示航路点或定位点；D(i～i-1)表示i定位点到i-1定位点的距离；Gri表示i航段最佳下降梯度。

若此航段有关键障碍物限制，则不进行梯度优化。

通过将历史航迹数据进行预处理和特征分类，利用HCDT、DSW和HPO进行模型建立和计算，可获得初始多个水平航迹、高度剖面和速度剖面，为飞行航迹生成提供基本参数。

3 实验设计

根据4D飞行路径动态规整模型设计仿真实验，具体如下。

(1)水平飞行路径实验：使用现有历史雷达航迹进行动态时间规整，对规整后的结果进行层次聚类，运用层次聚类获得的结果结合仪表进场航线，推导水平航迹数量和运行参数。

(2)速度剖面实验：利用动态空间规整算法，对现有历史雷达航迹上所获得的速度剖面进行规整，计算选出偏差最小的速度剖面作为标称速度剖面。

(3)高度剖面实验：使用现有历史雷达数据进行分析，整理空间内航路点的高度范围，将水平航迹参数与整理后各航路点高度范围进行结合，利用优化模型完成所对应的高度剖面设计。

(4)整理上述仿真实验中水平航迹、速度剖面，以及高度剖面信息，计算获得完整4D飞行路径。

3.1 水平飞行路径设计

采集实验对象机场近180 d航迹数据为样本，使用空客319为实验对象飞机，对现有历史雷达航迹进行时间规整和航迹聚类，建立现有历史雷达轨迹样本示意图，如图3所示。使用HCDT[式(1)～式(4)]对现有历史雷达航迹进行规整，再使用层次聚类对规整结果进行聚类分析，具体结果如图4所示。

图3 历史雷达航迹Fig.3 Historical radar trajectory

图4 历史航迹聚类结果图Fig.4 Historical trajectory clustering result map

为使计算结果更为集中且具代表性，将最小偏差平方和设置为0.15×1010来对航迹聚类分析进行剪枝，将剪枝后的一个树视为一个聚类，获得4个航迹聚类结果，使用均值判定航迹聚类结果，对照实验对象机场进场阶段飞行程序，最终获得4个水平进场路线设计，如图5所示。

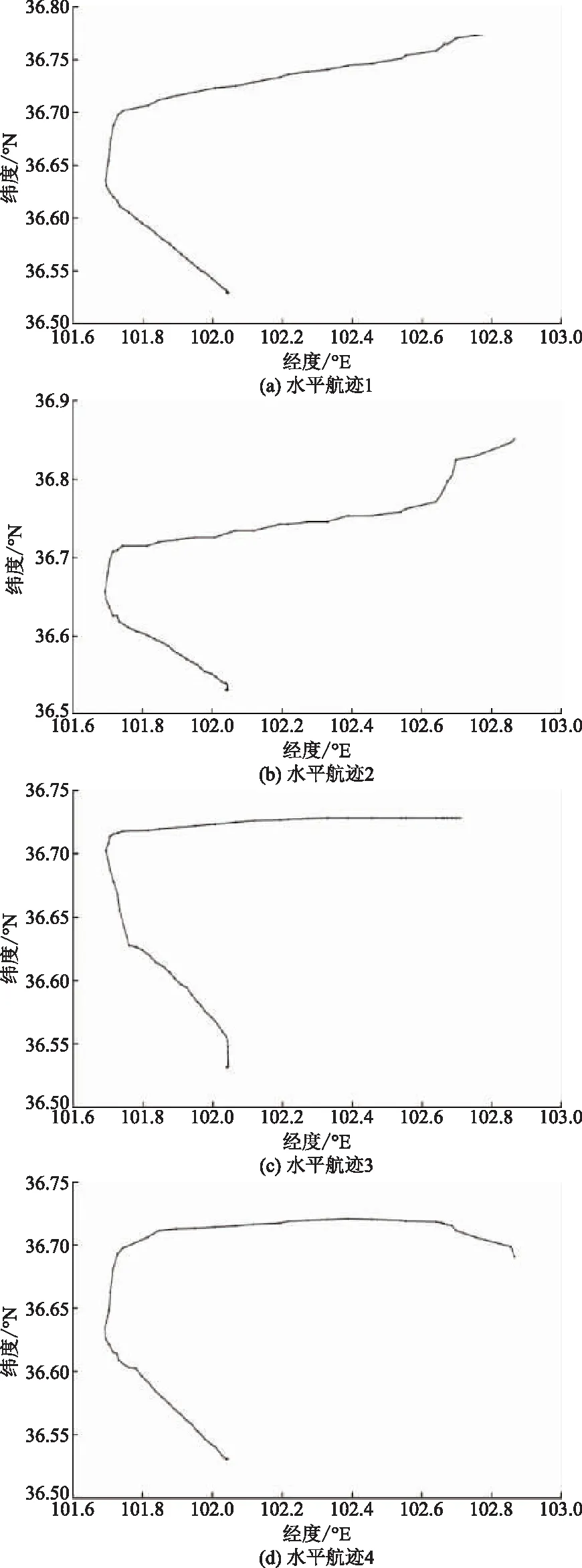
图5 A1进场水平航迹Fig.5 A1 approach horizontal trajectory

3.2 速度剖面设计

选择相同机场作为实验对象机场，实验对象飞机为空客319机型，采集现有历史雷达航迹，筛选飞行速度、空间水平位置、飞行距离等信息，建立原始飞行速度剖面示意图，如图6所示。

根据速度剖面推导获得DSW距离，通过式(12)对相关速度剖面进行偏差值计算，结果如表2所示。根据ICAO对飞行安全冲突值构建方式的建议，需在总系统误差中引入缓冲值加以保守处理，则仿真实验采用ICAO在进场阶段的建议值，BV取1海里(n mile)。集合偏差值进行分析，依照保守原则取偏差极小值构成标称速度剖面参数，由表2发现V4的偏差最小，则选取V4为标称速度剖面，建立标称速度剖面示意图，如图7所示。

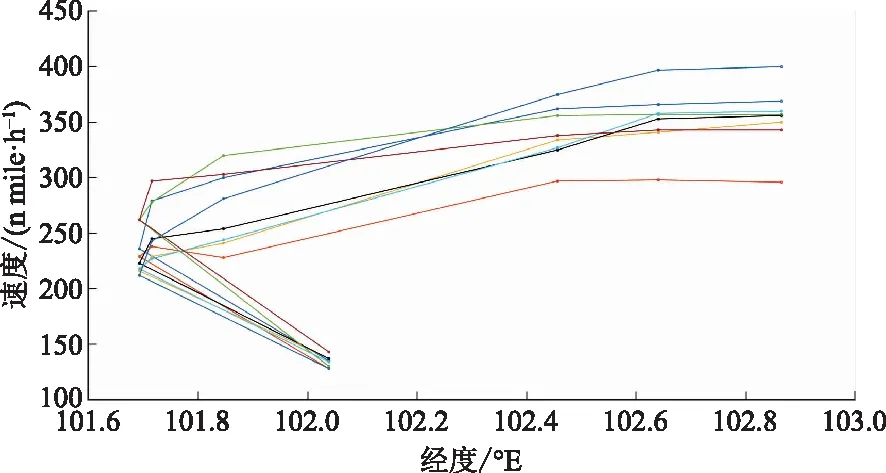
图6 原始速度剖面示意图Fig.6 Schematic diagram of the original velocity profile

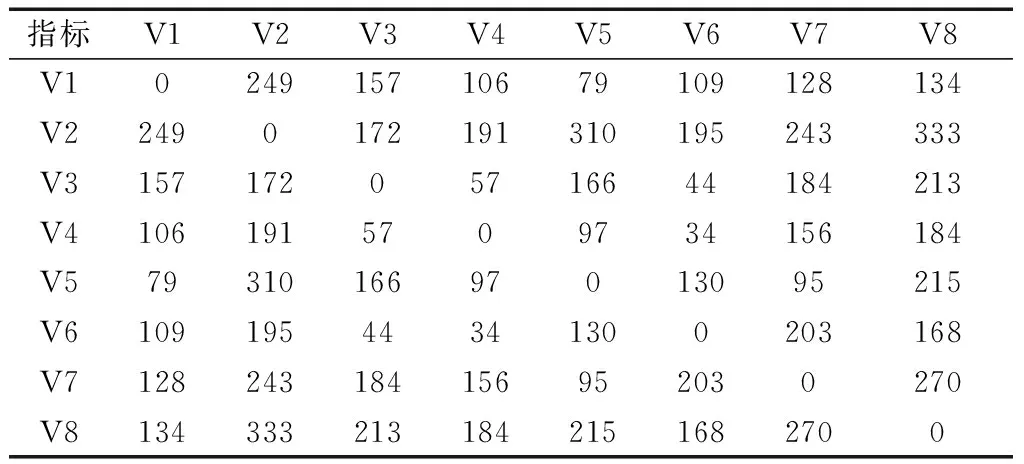
表1 DSW距离Table 1 DSW distance

表2 偏差Table 2 Deviation

3.3 高度剖面设计

选择相同机场为实验对象机场，采集进场阶段历史雷达航迹进行分析，获得进场航空器高度范围区间，如表3所示，建立高度剖面示意图，如图8所示。图8中A6为起始进近定位点(IAF)，A7为中间进近定位点(IF)，A8为最后进近定位点(FAF)。

采集进场和进近阶段障碍物数据，如表4所示。

按照ICAO对连续下降运行(continuous descent operations，CDO)的建议，利用HPO模型[式(13)～式(16)]对原始高度剖面进行优化，通过表4数据分析越障情况，设置进场航段最佳下降梯度为3%(<8%)，推导获得优化结果，相关数据如表5所示，建立优化后高度剖面如图9所示，其中A3为新增航路点。

图7 标称速度剖面Fig.7 Nominal velocity profile

表3 各航路点高度范围区间Table 3 Altitude range of each waypoint

ft为英尺,1 ft=0.304 8 m 图8 高度剖面示意图Fig.8 Schematic diagram of height profile

表4 障碍物数据Table 4 Obstacle data

表5 各定位点高度与距A1点距离Table 5 The altitude of each anchor point and the distance from point A1

ft为英尺,1 ft=0.304 8 m 图9 优化后高度剖面示意图Fig.9 Schematic diagram of optimized height profile

通过图8与图9对比可以发现，使用高度剖面优化模型实施优化后，使平飞段距离增加35.4 km，且下降梯度持续处于飞行标准安全值以内，保证飞行安全，提升了飞行经济性，符合约束条件的限制。

4 结果分析

根据水平航迹、速度剖面和高度剖面的实验设计和计算结果，完成实验对象机场由进场阶段至进近着陆过程中的飞行航迹优化，计算获得优化后航迹的所需飞行时间，选取4个典型优化结果形成距离和时间表，如表6所示。

根据优化结果开展计划到达时间(tPTA)和预计到达时间(tETA)对比和分析，设置阈值为5 s，用以衡量4D飞行路径的可靠性。结合表6优化结果分析发现，航迹4的飞行时间966 s与设定的飞行耗时(960 s)最相近，即tETA=966 s。计算tPTA和tETA的差值为6 s，超出预设阈值，因此对图7所示的标称速度剖面进行调整，修正后的速度如表7所示，修正后的标称速度剖面如图10所示。对照修正结果，使用标称速度剖面和编号4飞行航迹进行分析，计算获得飞行耗时为960.2 s，与tPTA所需飞行耗时960 s相差0.2 s，未超出预设阈值。在此结果之上，使用4D飞行路径动态规整算法(4DDW)优化生成4D飞行路径，利用历史雷达航迹数据生成实验对象机场进场航班原始飞行路径，如图11与图12所示。

表6 典型飞行航迹和所需运行时间Table 6 Typical flight trajectory and required running time

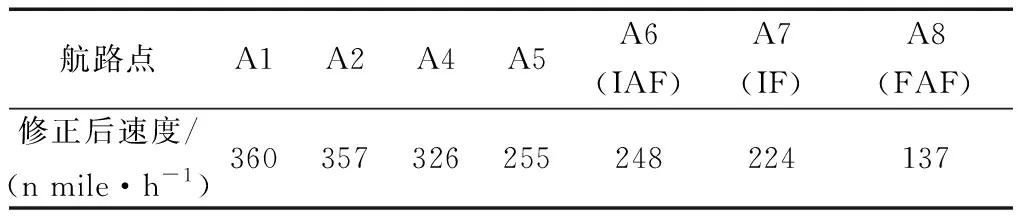
表7 修正后速度Table 7 Corrected speed

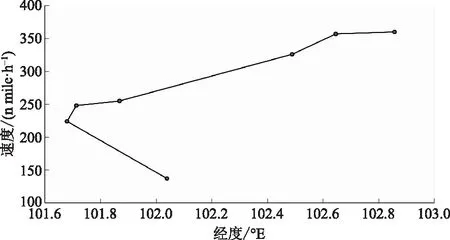
图10 修正标称速度剖面Fig.10 Correct the nominal velocity profile

ft为英尺,1 ft=0.304 8 m 图11 4D飞行路径规划图Fig.11 4D flight path planning diagram

ft为英尺,1 ft=0.304 8 m 图12 原始飞行路径图Fig.12 Original flight path diagram

根据仿真实验结果对比发现，原始飞行路径由A1起至A8点结束，其中没有A3定位点，整个飞行轨迹未对时间维度进行规划，而4D飞行路径由A1起至A8结束，A3定位点为新增点并且在A3开始下降，从A1至A3为平飞段，使得4D飞行路径可更靠近跑道，处于以较高飞行高度开始下降的姿态，提高了进场飞机机动性和经济性。此外，4D飞行路径在拥有时间维度的规划后，可有效提升进场航班排序，提高飞行安全，减少终端区的冲突与拥挤。

5 先进性描述

现阶段，相似研究主要集中在4D飞行路径构建方面，对算法的便捷性和完整性考虑层级有差异，其中使用基于计划到达时刻的四维航迹规划算法较为常见，是普遍采用的典型算法。根据表3以及原始飞行数据建立仿真实验，使用典型算法模拟生成4D飞行路径，计算结果如图13所示。

ft为英尺,1 ft=0.304 8 m 图13 典型算法和4DDW的飞行路径计算结果对比图Fig.13 Comparison chart of flight path calculation results between typical algorithm and 4DDW

对比计算结果发现，在飞行姿态方面，4DDW具备平飞和下降阶段，合理处理了越障安全和经济性的关系。在飞行路径结构方面，4DDW具备连续下降特征，优化了运行标准，提高了航空器飞行正常率。在空间路径范围方面，4DDW表现出空间范围收敛的特征，为提升空域容量提供了基础条件。

计算结果存在差异的原因有两点：①因为构建4DDW算法的三个剖面，均考虑了时间维度规划，使用了阈值预设和比较，使计算结果体现出对飞行时间和飞行距离的优化；②因为4DDW的高度剖面引入了CDO原则，将平飞、下降和越障分析加入到4D飞行路径计算中，可优化运行标准和收敛空间范围。由此可见，4DDW充分体现了在处理飞行路径预测等问题上的综合性和合理性，较当前常见算法具有先进性。