基于广义M-C强度准则的修正

蒋 磊，冉启来，杨前冬，卢雪峰，伍安杰

(1.贵州大学土木工程学院，贵州 贵阳 550025；2.中天环宇建筑设计有限公司遵义分公司，贵州 遵义 563000)

随着信息工程发展，人们在边坡、基坑的稳定性等方面使用数值模拟软件越来越频繁，大部分数值软件都是基于各种强度准则来实现模拟计算[1- 3]，因此对强度准则的要求越来越高。然而目前大多数准则都会有些许问题，如理论计算偏安全或危险，因π平面屈服轨迹不能保持非凸性、均存在奇异点等。

以Mohr-Coulomb强度准则(以下简记为M-C强度准则)为例，自发展以来，已引起了广泛的研究，它不仅适用于塑性岩石和脆性岩石的剪切破坏，还能放映出岩石的抗压强度远大于岩石的抗拉强度，但其最大缺点是只考虑了最大主应力和最小主应力的影响而忽略中间主应力的影响[4- 5]。针对此缺陷，郭建强与黄武锋等[6- 7]基于弹性应变能并考虑了中间主应力对岩石的影响，提出广义M-C强度准则(以下简记为GM-C强度准则)。该强度准则不仅弥补了M-C强度准则的不足，还从能量的角度分析岩石材料的变形破坏特性，并通过多种岩石进行三轴试验对数据验证，结果证明其精度明显皆高于M-C强度准则和D-P强度准则。尽管GM-C强度准则弥补了M-C强度准则大部分缺陷，但并非完美的强度准则，如其强度准则π平面屈服轨迹不能保持非凸性、均存在奇异点等问题，必须采取某些数学方法消除奇异点，才能建立数值模拟的本构模型。

基于此，本文将对GM-C强度准则的π平面屈服函数进行修正，以此消除GM-C强度准则π平面上屈服轨迹的奇异点。目前常见的消除奇异点方法可大致分为4类：①角隅模型修正法；②变换主应力法；③基于试验拟合出无角隅的屈服条件；④主应力回映算法。当前角隅模型修正法最为受诸多研究学者所用，其中Willian-Warnke椭圆角隅模型最为常见，如Willian和Warnke用椭圆角隅模型逼近M-C准则π平面上不规则六角形，以消除其角隅奇异点[8- 9]。

1 修正广义M-C强度准则

1.1 广义M-C强度准则

郭建强、黄武锋等[6- 7]基于弹性应变能并考虑了中间主应力对岩石的影响，提出GM-C强度准则，表达式如下：

(1)

式中，c、φ—材料的粘聚力、内摩擦力；θσ—罗德角；ν—拟合泊松比。

GM-C强度准则充分考虑了岩石的破坏伴随着能量过程，通过多种岩石进行三轴试验数据验证，证明其精度明显皆高于M-C强度准则和D-P强度准则。但GM-C强度准则π平面的屈服轨迹尖点产生的数值问题无法避免，成为其最大短板。

1.2 偏平面上的屈服条件

在主应力空间中，岩土屈服条件可用应力不变量I1、J2和θ洛德角表示[10]：

F=F1(I1)+F2(J2，θ)

(2)

F2(J2，θ)决定了π平面上的屈服轨迹的形状，F1(I1)=const时，即π平面上的屈服轨迹。当θ=const时，即子午平面上的屈服轨迹。

辛克维兹德-潘德(Zienkiewicz-Pande)提出辛克维兹德-潘德条件，表达式如下：

(3)

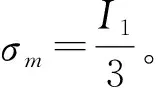
可将式(3)改写成二次型的一般式，如下：

(4)

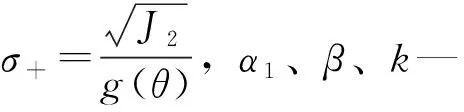
因此，形状函数表达式为：

(5)

式中，rc、qm—三轴压缩时π平面上的半径和q值；rσ、q—π平面上相应任意一θ的半径与q值。

通过真三轴试验来确定形状函数g(θ)，并且使用时需要同时满足以下3个条件：

(1)形状函数必须是凸函数，即要求：

(6)

g(-π/6)=1，g(π/6)=e

(7)

rσ(-π/6)=rc，r(π/6)=rl

(8)

(9)

式中，rl—三轴拉伸时π平面上的半径；e的取值范围是0.5～1。

(3)当θ=±π/6时，

g′(±π/6)=0

(10)

1.3 Willian-Warnke椭圆模型及其应用

Willian和Warnke提出椭圆角隅模型为[9]：

(11)

其中：

A=2(1-e)2cos(π/6-θ)

(12)

(13)

(14)

Willian和Warnke用式(11)来逼近平面上M-C强度准则不规则六角形。这一形状函数消除了角隅奇异点，且每处都外凸，与M-C准则不规则六角形外接。

因此采用Willian和Warnke的椭圆角隅模型代替M-C强度准则的形状函数g(θ)，对其屈服轨迹进行修正：

(15)

将(15)代入到(1)式便可得修正后的GM-C强度准则(以下简称为WM-C强度准则)：

(16)

WM-C是针对GM-C强度准则的π平面屈服轨迹不能保持非凸性和存在奇异点而提出的，目的是为了该准则能够更好地嵌入数值模拟软件。

2 WM-C强度准则的验证

2.1 WM-C强度准则光滑性验证

为了验证在不同拟合泊松比ν的情况下WM-C强度准则π平面上屈服轨迹的光滑性和外凸性，将WM-C强度准则与GM-C强度准则应用不同数据进行计算分析，如图1所示。

由图1可见有2个特点：①WM-C强度准则平面上的屈服轨迹能保持完全光滑性和外凸性，有效解决了GM-C强度准则平面屈服轨迹不满足完全光滑性和存在尖点处的问题，为后续应用于本构模型建立和嵌入数值软件计算带来方便。②WM-C强度准则平面上的屈服轨迹均与GM-C强度准则平面上屈服轨迹的6个角隅均相接，即在三轴拉伸和压缩条件下(θ=±π/6处)，WM-C强度准则与GM-C强度准则计算结果相同。

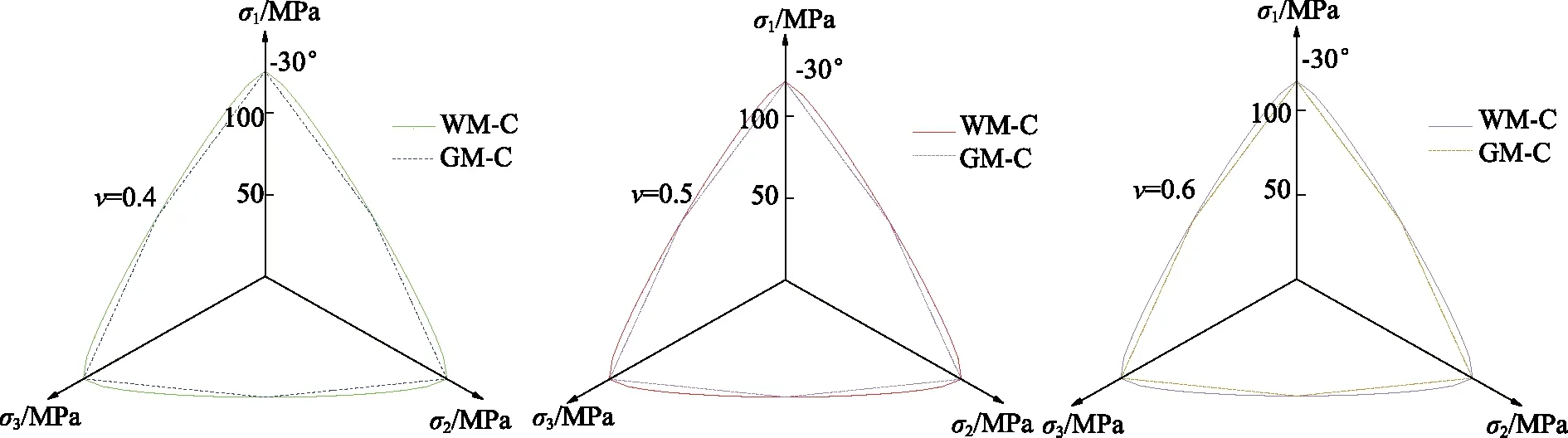
图1 不同拟合泊松比情况下π平面屈服轨迹对比

2.2 WM-C强度准则计算精度验证

为了验证WM-C准则的计算精度和适用性，利用红砂岩三轴试验[12]的数据进行验算，并将计算结果与GM-C准则计算结果进行对比。采用平均误差式评价各个准则计算误差，计算结果列于图2、表1。

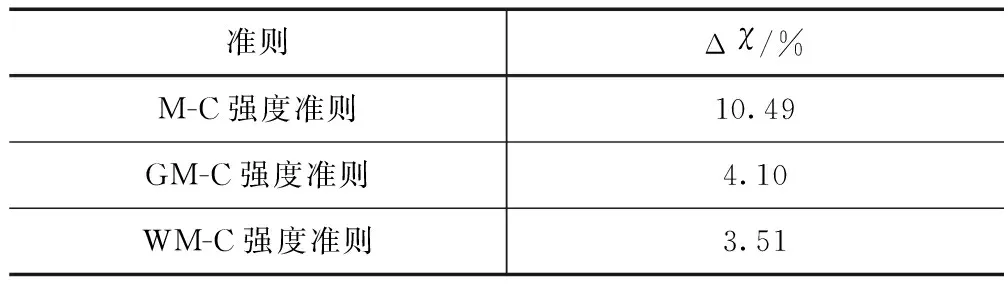
表1 真三轴试验平均误差

图2 W-MC与G-MC理论计算对比

采用WM-C强度准则计算红砂岩三轴试验破坏强度的平均误差为3.51%，不仅低于M-C强度准则计算的相应岩石的平均误差10.49%，更加低于GM-C强度准则计算的相应岩石的平均误差4.10%，可见，采用Willian和Warnke提出椭圆角隅模型修正的M-C强度准则在消除奇异点的同时，还能提高岩石破坏强度的计算精度。

3 结论

(1)采用Willian和Warnke提出椭圆角隅模型消除π平面屈服轨迹上的奇异点，建立WM-C强度准则。从π平面屈服轨迹对比来看，WM-C强度准则平面上的屈服轨迹能保持完全光滑性和外凸性，有效的解决了GM-C强度准则的短板问题，为后续应用于本构模型建立和嵌入数值软件计算打下基础。同时WM-C强度准则平面上的屈服轨迹均与GM-C强度准则平面上屈服轨迹的6个角隅均相接，即在三轴拉伸和压缩条件下(θ=±π/6处)计算结果相同。

(2)以红砂岩的试验为例，通过对比分析WM-C强度准则和GM-C强度准则的计算结果，WM-C强度准则在岩石破坏强度计算精度略高于GM-C强度准则，计算结果更为精确。WM-C强度准则为边坡、基坑等的稳定性提供了一定的可靠性。