基于BP-MOPSO 的散货船舱口圆形角隅疲劳强度优化设计

2022-05-05韩晓剑秦洪德邓忠超

船舶 2022年2期

李鹏韩晓剑秦洪德邓忠超

（哈尔滨工程大学船舶工程学院哈尔滨 150001）

0 引言

为了在散货船上获得更多的使用空间以提高利润，同时也方便货物装卸，散货船甲板上的货舱开口通常比较大，但由此其结构连续性便遭到破坏，不利于应力传递，极易形成应力集中，这使得舱口角隅的疲劳问题尤为严重。鉴于散货船在海运中无法替代的重要作用，散货船舱口角隅疲劳强度的优化是一个很有意义的研究问题。散货船甲板舱口角隅处的应力集中主要受以下因素影响：舱口宽度与整个船宽的比值、舱口长宽比、舱口角隅处的形状，其中角隅的几何形状对应力集中系数影响最大。

目前针对舱口角隅的优化思想主要分为2 种：一种是增加板厚，另一种就是改变角隅结构型式。倪敏杰根据CCS 规范对某超大型集装箱船舱口角隅的直角角隅、半圆形负半径角隅及新型角隅结构的疲劳强度进行了分析对比，得出一种较适宜的超大型集装箱船舱口角隅结构形式。陈景昊根据ABS、NK 和CCS 的疲劳规范的有关规定和建议，通过比较几种角隅形式疲劳寿命的方式对舱口角隅的结构形式进行了优化设计。樊祥栋等分析了CSR BC &OT 共同规范中的新规定，按照新规对某单壳散货船的甲板舱口角隅及纵向舱口围板趾端的疲劳强度评估及结构形式的多方案比较优化，认为近似圆弧形的角隅比抛物线型角隅在抵抗斜浪扭矩方面更有优势。以上工作均是基于上述两种优化思想，问题在于其只对有限种角隅形式进行了分析，未进行连续性的分析。孙力首次将BP 神经网络和MOPSO 寻优算法结合引入到超大型集装箱船的角隅疲劳优化中，以ANSYS 的子模型法提供大量子模型数据支持BP 神经网络的训练，模拟角隅应力及重量和结构参数间的连续非线性关系。

本文以1艘174 000载重吨散货船为实船算例，依据CCS《船体结构疲劳强度指南》（2018）对 6 号舱室舱口角隅的疲劳寿命进行计算，并基于BP-MOPSO 算法，设计了子模型法和全局模型法，从提高疲劳寿命和减轻结构重量的角度对比两种方法，对散货船的舱口角隅进行了优化，分析圆形角隅的结构参数对疲劳寿命的影响，得到一组较优的角隅结构形式。

1 有限元模型建立及角隅疲劳校核

1.1 三舱段有限元模型

目标散货船主要参数如表1 所示。

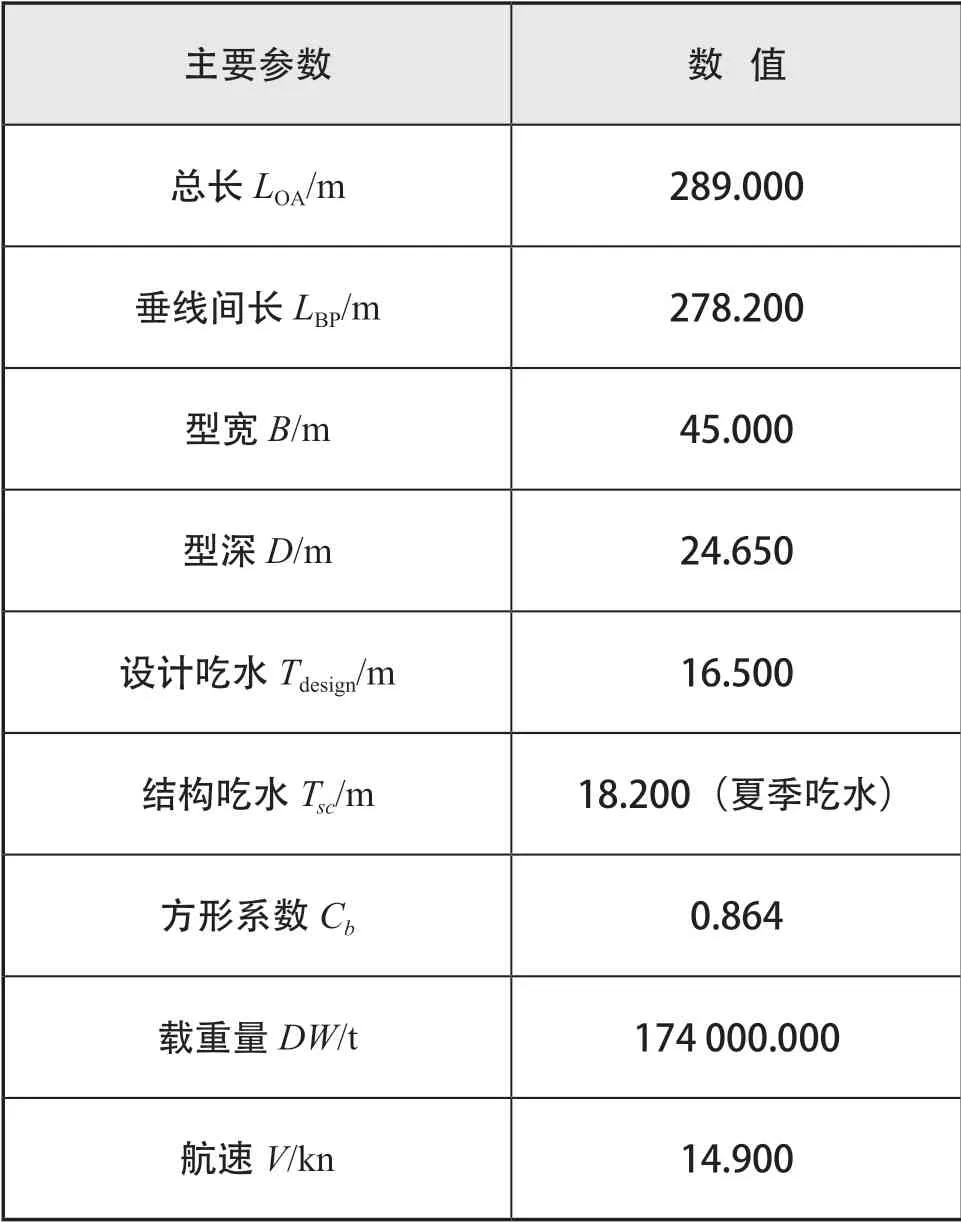
表1 散货船主要参数

依据CCS《船体结构疲劳强度指南》（2018）5.2 节中的规定建立三舱段有限元模型如下页图1所示，舱口角隅的精细化模型如下页图2 所示。原船舶角隅无过渡结构，先增设半径为1 m、板厚为 36 mm 的初始圆角过渡结构。

图1 三舱段有限元模型

图2 角隅精细化模型

1.2 初始角隅寿命计算

结合该散货船的装载手册，选取均匀满载、两端装载、中间装载和正常压载4 种装载工况，以及中拱迎浪、中拱随浪、中垂迎浪和中垂随浪4 种载荷工况，共组合出16 种计算工况。

根据CCS 疲劳指南将相应的总体载荷和局部载荷施加于有限元模型后，计算处理得到6 号舱室舱口4 个角隅的疲劳寿命。根据角隅直角顶点的坐标不同为角隅编号，即：角隅1（119.39 m，-10 m，25.34 m）；角隅2（119.39 m，10 m，25.34 m）；角隅3（113.86 m，10 m，25.34 m）；角隅4（113.86 m，-10 m，25.34 m）。各角隅疲劳寿命如表2 所示。

表2 初始角隅累计损伤度及疲劳寿命

由表2 可见：1 号角隅的疲劳问题比较严重，未能满足规范的20 A 寿命要求；2 号角隅接近满足；其他角隅均满足。

2 BP 神经网络和MOPSO 算法简述

2.1 BP神经网络

优化舱口角隅时，需建立舱口角隅应力和疲劳寿命与角隅的结构参数间非线性关系的代理模型。BP 神经网络（Error Back Propagation Neural Network）正以很强的非线性逼近及学习训练能力闻名，适用于模拟这种非线性关系。HORNIK K 等于1939 年在数学上已经证明具有单S 型隐含层和单线性输出层的BP 神经网络可以逼近任意非线性系统，故神经网络隐含层一般设为1 层。

本文采用平均相对变动值（ARV）来评估BP神经网络的预测效果。ARV 值越小，则BP 神经网络的训练效果越好。

2.2 MOPSO算法

本文对舱口角隅的优化包含角隅重量及角隅疲劳寿命或角隅应力多个目标函数，属于多目标优化的问题，而多目标粒子群优化算法（Multi-Objective Particle Swarm Optimization，MOPSO）正应此而生。MOPSO 算法由粒子群算法（PSO）改进而来，COELLO C 等于2004 年提出了具有里程碑意义的MOPSO。KENNEDY J等于1995年提出了PSO算法。PSO的基本思路是模拟自然界中鸟群搜寻食物的过程来找到单目标优化的最优解，通过计算机程序模拟种群中的个体与群体，具有原理简单、收敛迅速等优点。

3 舱口角隅优化

3.1 子模型法

子模型法是通过拉丁超立方抽样法（Latin Hypercube Sampling，LHS）获得设计变量的样本空间，以BP 神经网络模拟角隅应力和设计变量之间的非线性关系，易得角隅重量与设计变量的函数关系；以MOPSO 算法进行舱口角隅优化设计，将Pareto 前沿中的数据归一化处理后，采用包含权重的最小距离法，从非劣解集中得到一组最优解。

3.1.1 子模型建立

本文旨在对圆形角隅的疲劳强度进行探究，故设计变量为角隅半径/mm 及板厚/mm。设计变量取值范围见表3 所示。

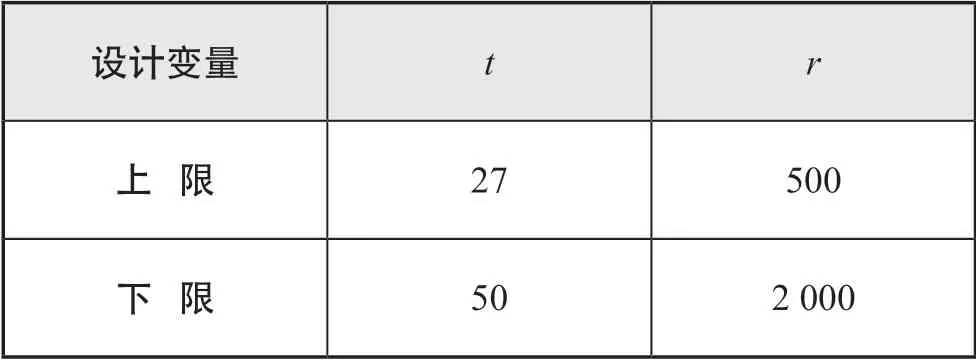
表3 设计变量的取值范围mm

前人一般使用ANSYS 中的子模型法，本文探索出一种使用Patran 建立大量子模型的方法。以1.2 节中的角隅形式为基础，考虑到1 号角隅寿命最短，将其在另一模型数据库中重新参数化建立，即为子模型。由1.2 节中的结果数据可知，均匀满载中拱时热点合成应力最大，故以此工况下角隅边界节点的位移作为强制位移施加于子模型中。为验证初始子模型的正确性，首先对比原模型和子模型中1 号角隅的位移等值线图（如图3 和图4 所示），可见两者之间的趋势和大小基本一致；然后对比两者的Von Mises 应力云图（如下页图5和图6 所示），其角隅自由边最大应力相差0.25%，两者之间的趋势及大小基本一致。由此，子模型的正确性得到验证。

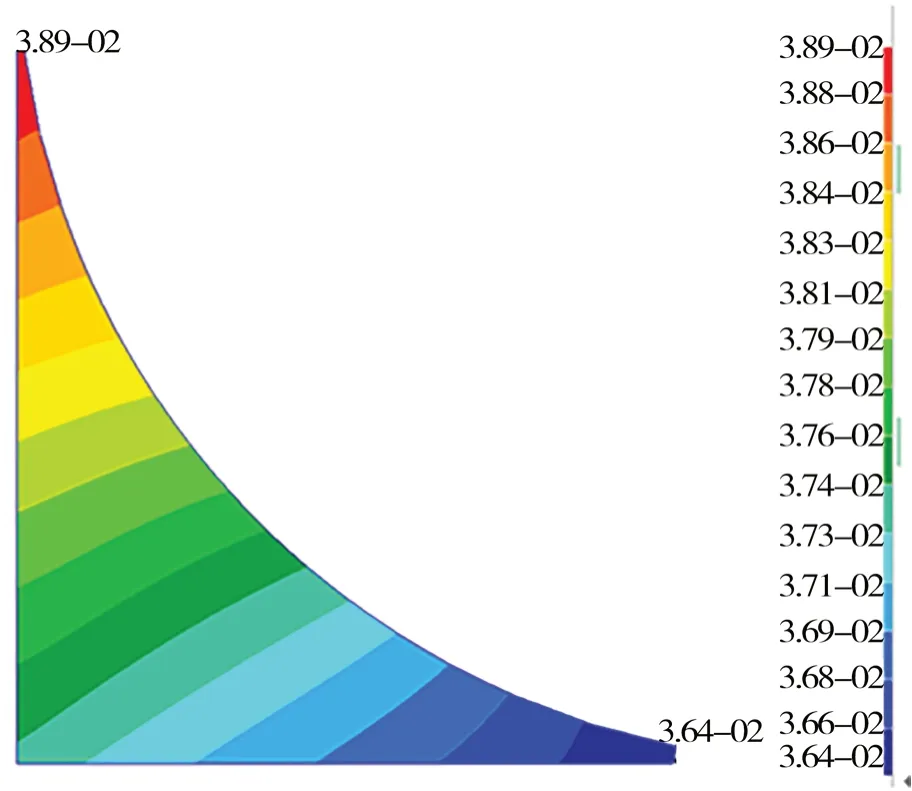
图3 原模型中角隅1 位移云图

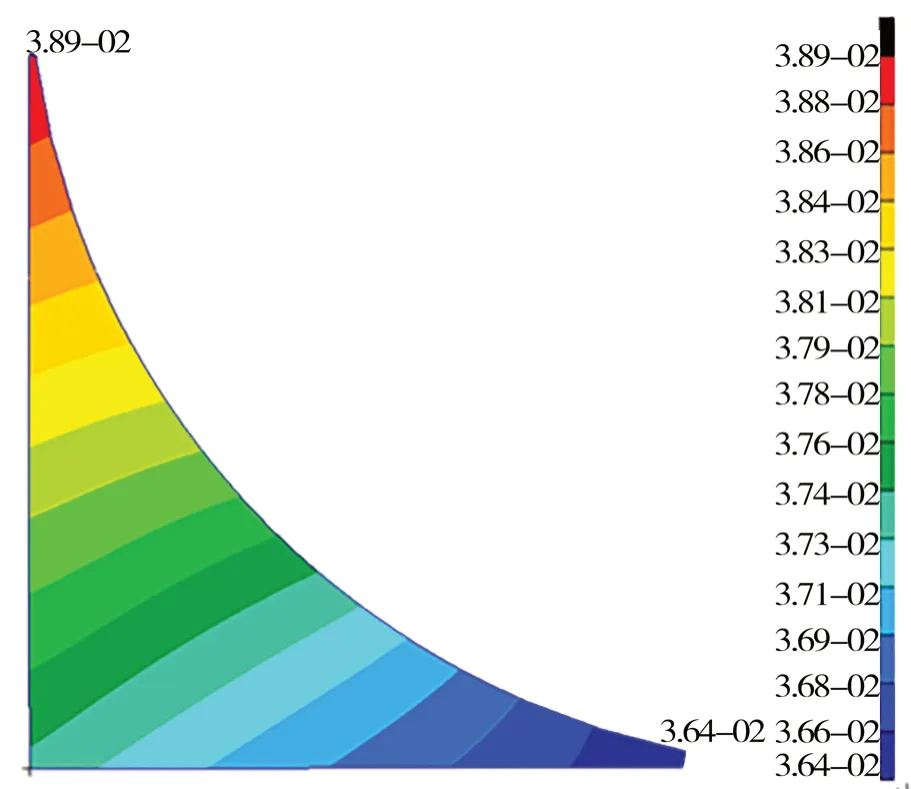
图4 子模型中角隅1 位移云图

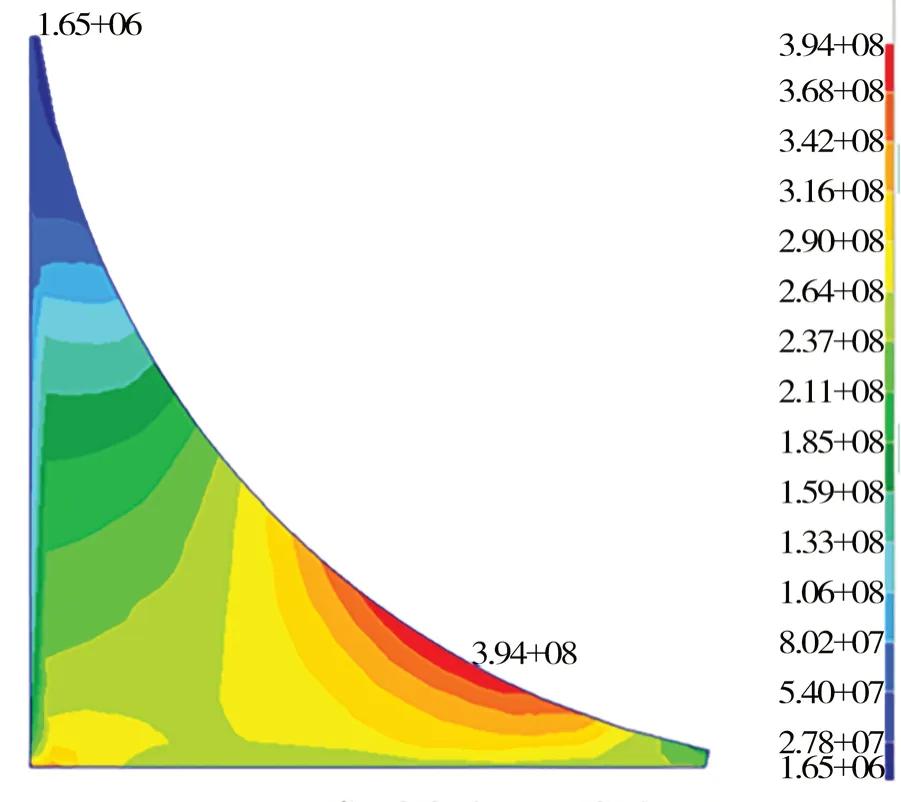
图5 原模型中角隅1 应力云图

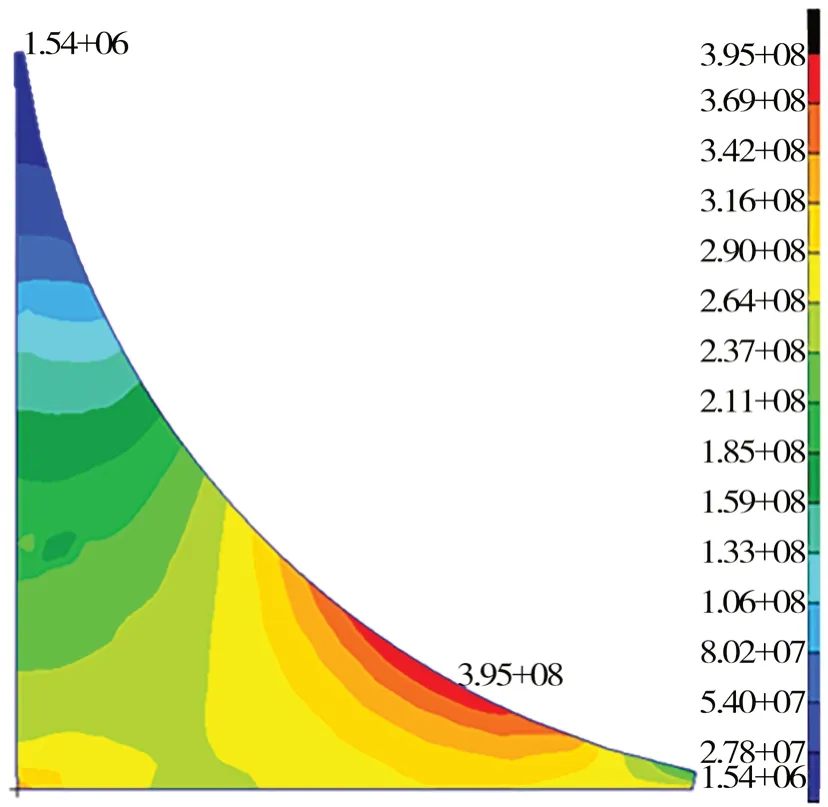
图6 子模型中角隅1 应力云图

为得到训练BP 神经网络的大量数据，通过Patran 中Group 功能将子模型大量生成在子模型空间中，变换参数由LHS 抽样获得；通过PCL 函数，将LHS 抽样中的板厚赋给对应角隅。由于每当角隅结构形式发生变化时，其边界节点位移即发生变化。考虑到角隅周围舱口的结构刚度度强于角隅，认为边界节点的位移变化不大具有一定合理性。为方便设置，此处假定边界条件不变，以半径1 m、厚度36 mm 角隅的角隅边界节点的位移作为强制位移施加于不同子模型中。

3.1.2 训练BP 神经网络

首先，使用LHS 抽样获得3 组设计变量，第1、2、3 组分别有500、1 000、2 000 个样本数据。在Patran 中各自参数化建模计算后，得到对应的应力云图，图7 为第2 组部分角隅的应力云图。然后以角隅半径、板厚作为输入层，提取各角隅155 号单元的中心点应力作为输出层，每组各取15%数据作为测试集，神经网络隐含层设为1 层。采用梯度下降法进行训练，训练次数设为1 000，学习速率设为0.01，训练目标最小误差设为1×10。经多次试验，将隐含层节点数设为10。建立一个2-10-1网络结构。

图7 第2 组部分角隅的应力云图

各组训练样本的训练结果如表4 所示，由平均相对变动值（ARV）对比，选择训练样本个数为 1 000时训练的网络作为接下来优化算法的目标函数。

表4 各训练样本的训练结果

3.1.3 MOPSO 算法优化

子模型法中，舱口角隅的多目标优化数学模型如下：

式中：()为单个舱口角隅的重量，kg；(x)为3.1.2节中训练得到的BP神经网络。显然：

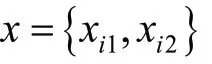
式中：为板厚，mm；为角隅半径，mm；为材料密度，kg/mm。

MOPSO 中的参数设置为：粒子群大小为100，外部档案大小为100，最大迭代次数为200，权重系数为0.4，学习因子1 与2 均为2，变异率为0.1。BP-MOPSO 优化得到的Pareto 前沿面如图8 所示。

图8 子模型优化得到的Pareto 前沿面

由于应力和重量之间的数值差距较大，为保证两个函数在未加入权重参数前对最小距离的贡献一致，消除两组目标函数结果本身数值上的较大差异对最小距离的影响，见式（3）和式（4）。

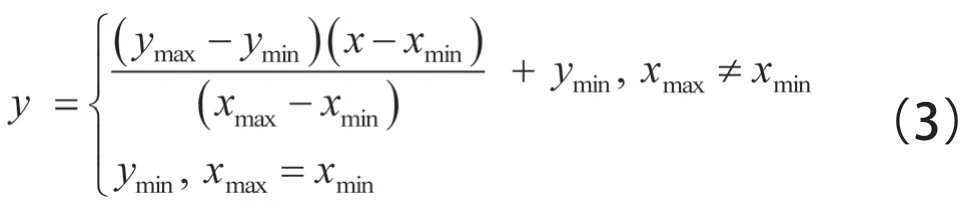
式中：为归一化的上限；为归一化的下限；为数据的最大值；为数据的最小值。

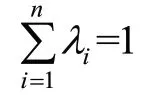
将两组数据使用式（3）所述映射将数据归一化到0，1 之间。最后，按式（4）采用含有权重的最小距离法从Pareto 前沿面中选取最优结果，表5为不同权重下设计变量的优化结果，优化后BP 神经网络的预测值与有限元计算结果的误差对比如表6 所示。

表5 不同重量权重下设计变量的优化结果

表6 BP 神经网络预测值与有限元计算结果的误差对比

误差最大为0.005 9%，在允许范围内，因此认为BP 神经网络预测准确。

考虑到相对于整体船舶质量，该处结构重量所占比例较小，取=0.1 和=0.9 时的设计变量在全局模型中对角隅进行修改，与1.2 节中初步设计的角隅对比如下页表7 所示。相比原结构，=0.1 时，角隅重量增加了119.54%，寿命提升了19.25%；=0.9 时，角隅重量减少了15.66%，寿命减少了7.60%。可见，减轻角隅重量与提升角隅疲劳寿命之间矛盾很深，除非大幅度增加角隅重量，疲劳寿命很难有较大提升。

表7 权重对优化的影响及优化前后对比

3.2 全局模型法

全局模型法即直接在原模型中修改角隅结构形式，计算角隅的疲劳寿命。

3.2.1 全局模型建立

由表3 中的设计变量取值范围，计算了30 种角隅的结构形式在角隅1 处的疲劳寿命，参见表8；定义了一个评价参数寿命重量比用于评估不同形式的角隅，显然其值越小表明角隅越优秀。疲劳寿命随角隅半径和板厚的变化如下页图9 所示。当板厚一定时，随角隅半径的增加，疲劳寿命的增加趋于平缓；当角隅半径一定时，随板厚的增加，疲劳寿命的增加同样趋于平缓。寿命重量比随角隅重量和疲劳寿命的变化如下页图10 所示。随角隅重量的增加，疲劳寿命的增加越来越平缓，寿命重量比逐渐下降，即单位结构重量对疲劳寿命的贡献越来越低，见式（5）。

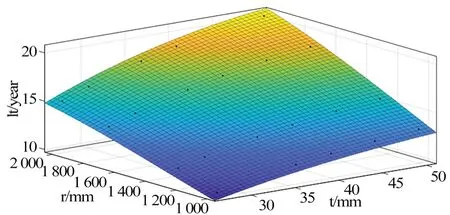
图9 疲劳寿命随角隅半径和板厚的变化

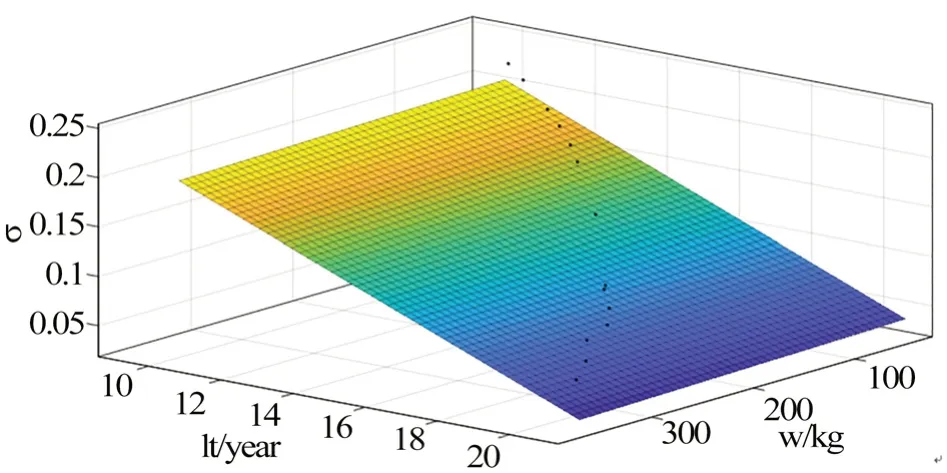
图10 寿命重量比随角隅重量和疲劳寿命的变化

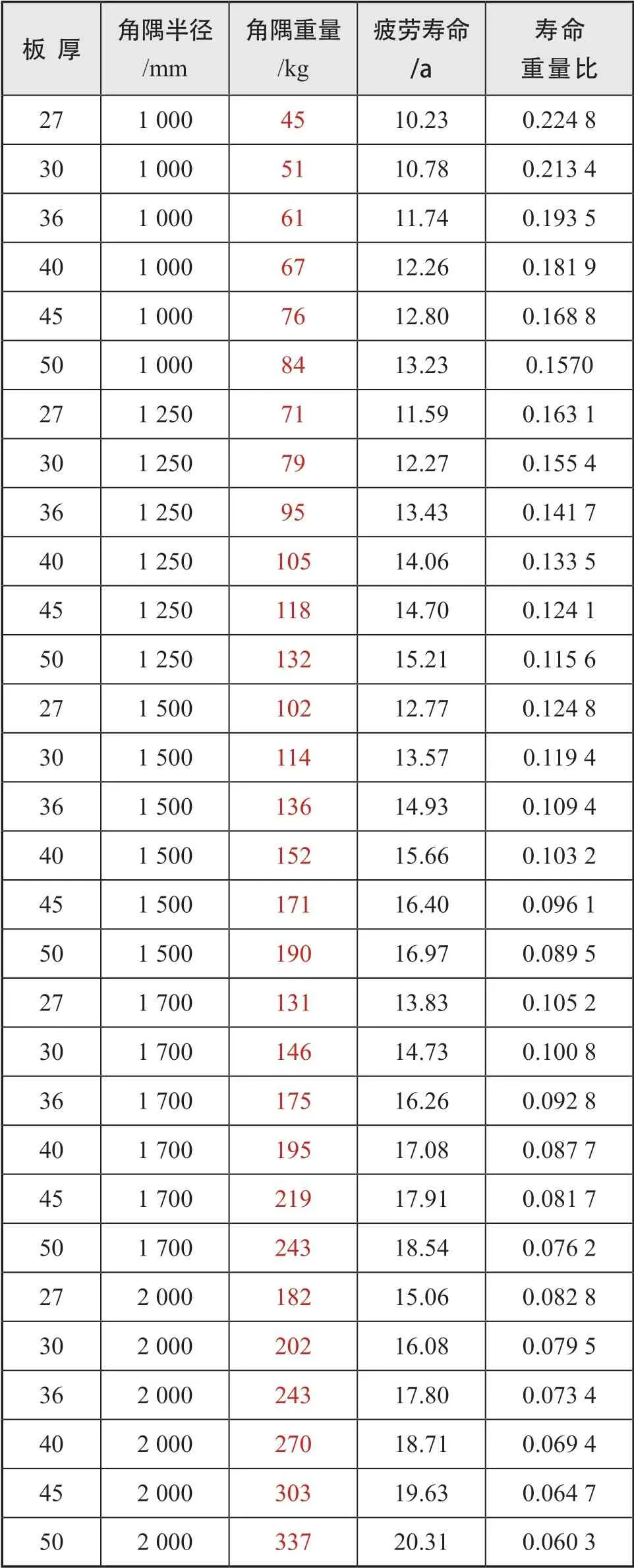
表8 30种角隅的参数及疲劳寿命

式中：为角隅1的疲劳寿命，a；为角隅重量，kg。

3.2.2 训练BP 神经网络

使用表8 中的数据，同3.1.2 中的方法，将输出层改为疲劳寿命。由于数据较少，将全部数据作为测试集，经多次实验，隐含层节点设为6，其余参数与3.1.2 中相同。由此建立一个2-6-1 网络结构。训练结束后，平均相对变动值ARV=4.14×10。

3.2.3 MOPSO 算法优化

全局模型法中，舱口角隅的多目标优化数学模型如下：

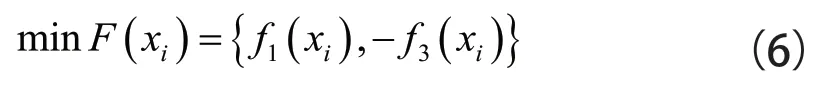
式中：(x)为根据3.2.2 节中训练得到的BP 神经网络；疲劳寿命与设计变量之间均为正相关关系，故添加负号，使MOPSO优化时()向最小值优化，()向最大值优化。

设计变量范围与MOPSO 参数设置同3.1.3 节。最终优化得到的Pareto 前沿面如图11 所示。

图11 全局模型优化得到的Pareto 前沿面

表9为不同重量权重下设计变量的优化结果。结果中，角隅1疲劳寿命BP神经网络的预测值与有限元计算结果的误差对比见下页表10。最大误差值为0.030 2%，在可接受范围，认为BP神经网络预测准确。

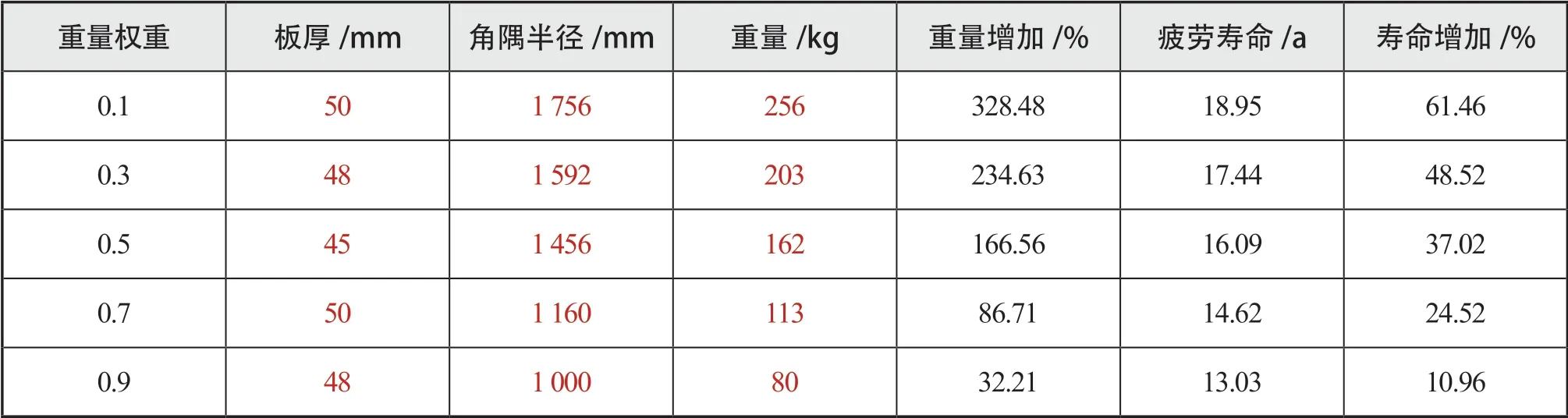
表9 不同重量权重下设计变量的优化结果

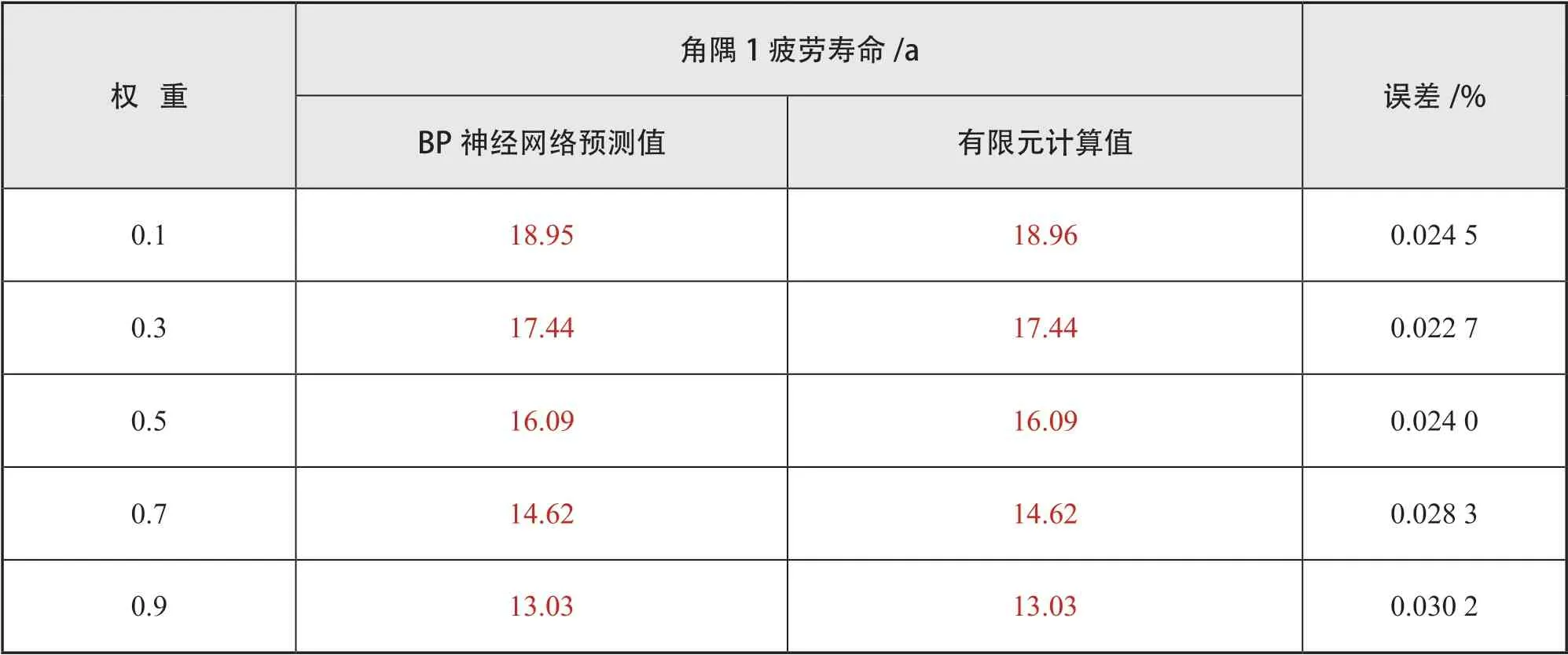
表10 BP 神经网络预测值与有限元计算结果的误差对比

3.3 两种方法的对比分析

3.3.1 子模型法优缺点

子模型法的优点在于能够获取大量原始数据训练BP 神经网络，手工操作工作量相对较少，可以保证BP 神经网络预测值的精确性。缺点在于子模型的边界节点的位移约束条件是基于假定而来的，对板厚这一设计变量敏感度不高，未能反应板厚变化对应力的影响；不能直接用BP 神经网络拟合角隅疲劳寿命与角隅结构参数之间的非线性关系，只能用某一对疲劳损伤度影响较大的计算工况下的应力来反映寿命。

3.3.2 全局模型法优缺点

全局模型法的优点在于更直接地反映了角隅结构参数的变化对疲劳寿命的影响，通过训练BP神经网络获得了角隅结构参数和疲劳寿命之间的非线性关系，较为直观；对两个设计变量对疲劳寿命的影响反应均较好。缺点在于用来训练的原始数据较少，无法通过比较评估参数选择更优秀的BP 神经网络，可能会导致BP 神经网络准确度不足，但由实际对比可知其仍误差均较小，原因可能是训练BP 神经网络时所取的设计变量范围较小，30 组数据足够BP 神经网络模拟，且在MOPSO 调用BP 神经网络时，未超出训练时的变量范围，因此即使网络的泛化性不好对预测结果也没有影响；同时手工操作工作量较大，角隅处的有限元模型及网格细化一般均需手工建立。

综上所述，认为全局模型法优化结果的置信度更高。以全局模型法的优化结果为准，得到一组考虑重量权重的最优解，如上页表9所示。