某轨道车辆用空调系统管路动态特性分析方法与试验验证
2022-09-29郭志伟
郭志伟,张 杰,王 鹏
(山东朗进科技股份有限公司,山东 青岛 266071)
在轨道车辆用空调中,管路设计是轨道车辆用空调整机设计的核心内容之一。一旦管路发生断裂,极易导致空调无法正常运行。在导致管路断裂的众多因素中,压缩机旋转产生的机械共振是管路断裂的最主要原因[1]。早期对轨道车辆用空调系统管路的设计主要考虑系统性能等因素的影响,对管路的动态特性的设计过多地依赖设计经验,目前利用有限元仿真技术与试验技术相结合的方法研究管路振动问题已成为一种趋势[1-3]。本文通过上述方法,对某轨道车辆用空调系统管路的动态特性进行识别,指导管路优化设计,同时验证仿真模型的可靠性。
1 基本理论
对于小阻尼系统,其固有频率和振型与阻尼、外部载荷无关,结构动力学方程可简化为:
(1)
式中:{x}——系统的位移,{x}=[x1,x2,…,xn]T;

[M]——系统的质量矩阵;
[K]——系统的刚度矩阵。
式(1)通解可表示为:
{x}={φ}sinωt
(2)
其中,
{φ}=[φ1,φ2,…,φn]T
(3)
式中:ω——系统的固有频率,rad/s;
{φ}——系统的振型向量。
将式(2)代入式(1)可得,
(-ω2[M]+[K]){φ}={0}
(4)
式(4)具有非零解的条件为,
|-ω2[M]+[K]|=0
(5)
求解式(5)即可得到系统的固有频率,进而得到n阶固有频率所对应的振型{φ}n。
2 结果分析
2.1 仿真结果
在样机生产之前,对某轨道车辆用空调系统管路进行模态仿真分析,提取该管路的动态特性。在分析中,为了避免模型过于复杂,同时为了更好模拟管路真实安装状态,将空调压缩机机体简化为等刚度、等质量空心圆柱体,压缩机减振垫上下表面、管路末端简化为固定约束,四通换向阀卡箍固定处简化为弹性支撑约束[4-5]。压缩机、减振垫、管路材料分别为TP2M紫铜、AISI304不锈钢、EPDM。表1为材料属性。图1为管路仿真三维模型。

表1 管路材料属性表

图1 管路仿真三维模型
图2(a)至(d)为该管路前4阶模态振型,前4阶模态固有频率分别为32.5 Hz、56.27 Hz、60.63 Hz、75.68 Hz。前3阶模态固有频率均在压缩机常运行工作频率范围内,存在较大共振风险。因此,采用增加弹性支撑约束(卡箍)的方式对该管路进行优化,卡箍添加在各阶振型位移最大处[6]。由于腔体空间的限制,第3阶模态振型位移最大处无法增加卡箍,优化模型如图3所示。
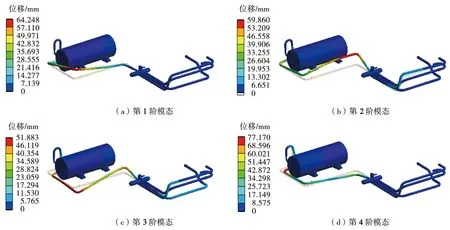
图2 管路前四阶模态振型

图3 优化后管路仿真三维模型
对优化后的管路进行模态仿真分析,图4为前4阶模态振型。前4阶模态固有频率分别为61.68 Hz、101.79 Hz、107.26 Hz、128.3 Hz。可以看出,弹性支撑约束的效果提高了整个管路系统的刚度,从而提高了管路系统的固有频率。优化后的管路只有第1阶模态固有频率处于压缩机常运行频率范围内,仍存在共振风险,需进一步进行优化。由于第1阶模态振型位移最大处无法增加卡箍,因采用改变管路形式即缩短管路长度的方法提高其固有频率。第二次优化后的管路模型如图5所示,约束点如第一次优化模型卡箍固定位置。

图4 优化后的管路前四阶模态振型

图5 第二次优化后管路仿真三维模型
对第二次优化后的管路进行模态仿真分析,图6(a)至(d)为前4阶模态振型,前4阶模态固有频率分别为82.319 Hz、129.77 Hz、139.31 Hz、159.16 Hz,与第一次优化后的管路的模态参数相比较,固有频率分别提升33.4%、21.6%、29.9%、24.0%。同时,第1阶模态固有频率已超过压缩机最大工作频率,共振风险大大降低。
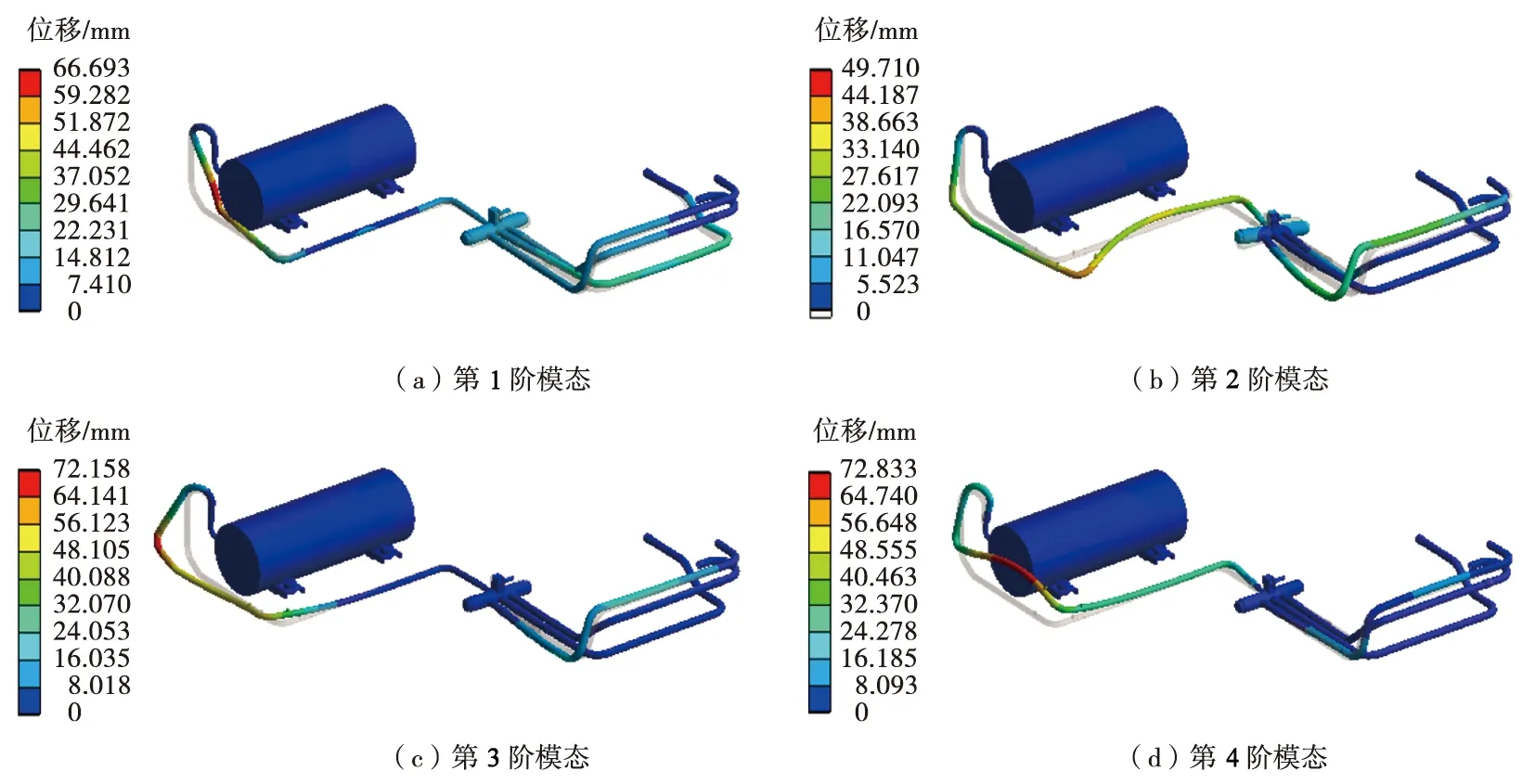
图6 第二次优化后的管路前四阶模态振型
2.2 试验测试结果
为验证仿真分析的可靠性,采用北京东方振动和噪声技术研究所Coinv DASP V11测试软件及INV3062-C1(L)型控制仪,对第二次优化后的管路进行模态试验。图7为管路测点布置分布图,选取28个测量位置,每个位置进行三个方向的测量,共进行84次敲击。为避免ICP加速度传感器布置在模态振型节点上从而导致某阶模态丢失,此次试验采用固定多个加速度传感器,移动力锤的方式进行模态试验,传感器1、2分别布置在测点10、测点23。模态试验振型如图8(a)至(d)所示,模态仿真分析与模态试验结果对比如表2所示。
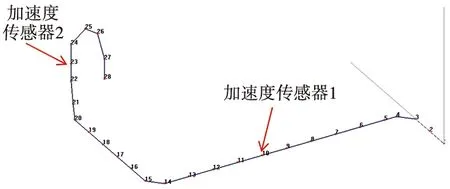
图7 管路测点位置分布图

图8 第二次优化后的管路前4阶模态振型(模态试验)

表2 模态仿真与模态试验固有频率
从表2可知,模态仿真与模态试验所得到的结果在200 Hz内基本吻合,最大误差出现在第三阶,误差为8.53%。综上,利用有限元方法分析管路模态的方法是可靠的。
在样机阶段,采用上述仪器及设备对两次优化后的管路进行振动试验,图9和图10分别为两次优化后的管路ICP加速度传感器布置位置,Coinv DASP V11测试软件可将振动加速度一次积分转化为振动烈度。测试发现:

图9 第一次优化后的管路加速度传感器测点布置

图10 第二次优化后的管路加速度传感器测点布置
(1) 对于第一次优化后的管路,在压缩机工作频率为60~65 Hz时,该管路振动烈度较大,最大值接近100 mm/s,这表明该管路此时处于共振区间内,在其他频率点,管路振动正常,且振动烈度均不超过30 mm/s,图11为管路振动烈度随压缩机工作频率的变化规律。振动试验测得的共振区间范围与第1阶模态仿真结果相对应。
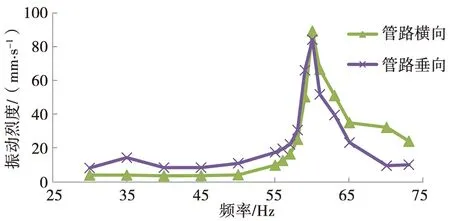
图11 第一次优化后的管路振动烈度
(2) 对于第二次优化后的管路,在压缩机工作频率为75~79 Hz时,该管路振动烈度逐渐增加,进入共振区间,在其他频率点,该管路振动正常。图12为管路振动烈度随压缩机工作频率的变化规律。振动试验测得的共振区间范围与第1阶模态仿真结果相对应。
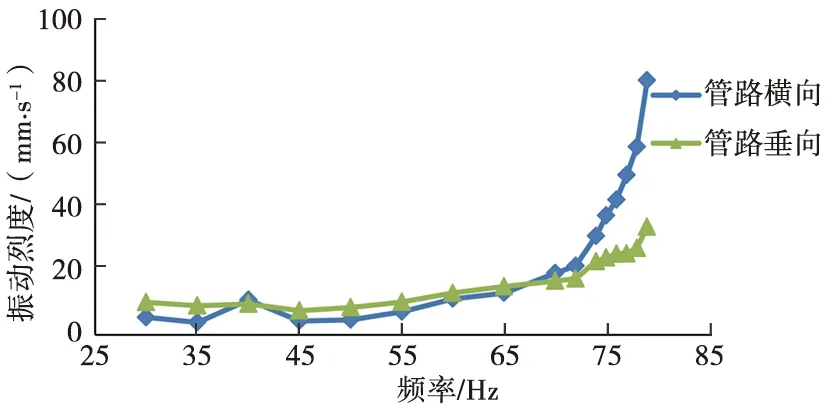
图12 第二次优化后的管路振动烈度
通过振动试验的结果进一步验证了仿真分析的可靠性。
3 结论
为避免空调压缩机工作产生的激振力频率与管路固有频率相近产生机械共振,采用有限元仿真与试验测试相结合的方法对某轨道车辆用空调系统管路进行优化设计,取得显著效果。
(1) 模态仿真结果显示优化前管路在压缩机常运行频率范围内存在较大共振风险。通过优化,仿真结果显示该管路第1阶模态固有频率提升至82.319 Hz,已无共振风险。
(2) 在模态试验中,该管路最终模型的第1阶模态固有频率与仿真结果误差为2.33%,同时振动试验结果也与仿真结果相吻合。在后续管路设计中,可直接通过有限元方法确定管路的动态特性,避免管路发生共振现象,同时也可省略模态试验,节约时间成本。
(3) 本文主要研究了某轨道车辆用空调压缩机到四通换向阀之间的管路,空调其他管路系统亦可采用此方法进行优化设计。
