不同角度含裂纹损伤钢构件拉伸试验与分析

昌毅，邹杨洋，江元琪，阳程，余柳明，高金贺

(1.核技术应用教育部工程研究中心(东华理工大学)，南昌 330013；2.东华理工大学土木与建筑工程学院，南昌 3300133.中冶(上海)钢结构科技有限公司，上海 201908)

近代以来，在工程中，钢材一直都是中外使用较多的材料[1]。在实际工程中，由于钢材中存在裂纹，并且，当裂纹发生失稳扩展时，将极大地降低结构的极限承载能力[2-4]，从而造成大量的经济损失和人员伤亡。已有研究者对特定角度的含裂纹损伤钢构件进行了试验研究[5]。然而，在实际工程中，由于裂纹出现的角度是随机的，因此针对不同角度的含裂纹损伤钢构件进行拉伸试验是非常有必要的。

通过大量事故分析，钢材由于其内部存在裂纹损伤，甚至可能导致发生脆性断裂现象。断裂力学可以很好地解释含裂纹损伤钢构件发生脆性断裂的力学原理[6]，但是没有通过具体的试验来进行验证。针对含裂纹损伤钢构件的研究，多是从研究它的剩余极限强度开始的[7]。Paik等[8]提出了较为简单的计算剩余极限强度的公式，并且随着有限元软件的发展。文献[9-12]运用有限元软件对含裂纹损伤钢构件进行分析，提出了剩余极限强度的计算公式。由于以往研究中均假定含裂纹损伤钢构件的屈强比是固定的，而这与实际情况不符。因此，针对屈强比发生改变这一现象，可以结合试验对剩余极限强度展开进一步的研究分析。

综上所述，基于不同裂纹角度和屈强比随裂纹长度变化的情况，提出一种精确的含裂纹损伤钢构件剩余极限强度计算公式来分析含裂纹损伤钢构件发生脆性现象情况是非常有必要的。

1 试验内容

拉伸试验的材料为Q235钢和Q355钢，裂纹的类型为I型裂纹(即张开型裂纹)且为中心穿透裂纹。裂纹长度为2c，构件宽度为2b。以钢构件裂纹长度与宽度的比作为相对裂纹长度，即c/b，裂纹方向与钢构件受拉方向所形成的角度为裂纹角度α。图1为相对裂纹长度为c/b，裂纹角度为α的含裂纹损伤钢构件示意图。

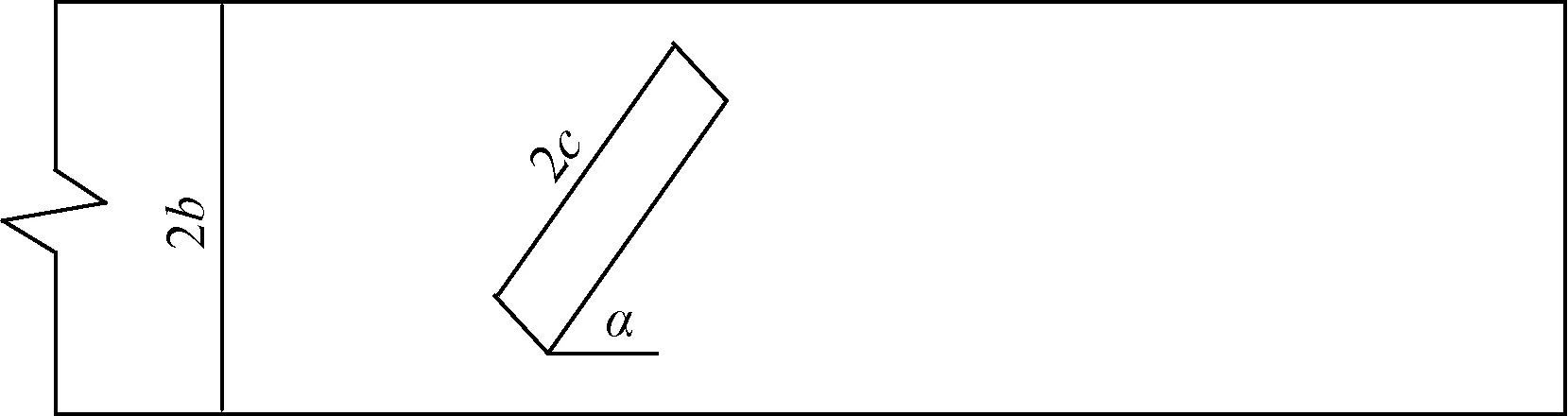
图1 相对裂纹长度和裂纹角度示意图Fig.1 Schematic diagram of relative crack length crack angle

含裂纹损伤钢构件的设计宽度为40 mm，裂纹角度共计6种，分别为15°、30°、45°、60°、75°和90°。根据《金属材料拉伸试验第1部分:室温试验方法》(GB/T 228.1—2020)[13]，相对裂纹长度的取值一般控制在0～0.5，所以本试验的相对裂纹长度也控制在这个范围内。含裂纹损伤钢构件的裂纹长度共计10种，分别为2、4、6、8、10、12、13、14、15、16 mm，且裂纹均处于试验构件的中心位置。图2为裂纹长度13 mm裂纹角度30°的含裂纹损伤钢构件。

通过改变上述10种不同裂纹长度或6种不同角度，共有60种情况，每种情况有5个试验构件，再分别对Q235和Q355两种不同钢材进行试验，共计600个试验构件。

试验采用SHT4305微机控制电液伺服万能试验机，控制应力速率为10 MPa/s。对无裂纹试验构件进行拉伸试验，得到Q235和Q355钢的拉伸性能指标，如表1所示。

R为钢构件弧形部分的半径图2 裂纹长度14 mm裂纹角度45°设计图与试验构件图Fig.2 The crack length 14 mm crack angle 45 degree test component

表1 Q235和Q355钢的拉伸性能指标Table 1 Tensile properties of Q235 and Q355 steel

2 试验结果分析

断后伸长率主要反应钢材的变形能力，可以用来判断含裂纹损伤钢构件呈现塑性或脆性性能[14]。通过试验来研究含裂纹损伤钢构件的断后伸长率与相对裂纹长度以及裂纹角度的关系。

2.1 裂纹角度和长度对断后伸长率影响

图3为相对裂纹长度相同时，不同裂纹角度的荷载-位移曲线。根据图3可知，在相对裂纹长度相同的情况下，裂纹的角度越大，含裂纹损伤钢构件的位移越小，越危险。

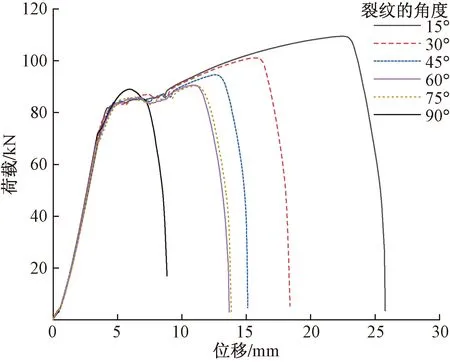
图3 不同角度下的荷载-位移曲线Fig.3 Load-displacement curves at different angles

根据试验数据分析，可以得到相对裂纹长度一定时，不同角度下含裂纹损伤钢构件断后伸长率如表2所示。

从表2可知，当裂纹角度从15°变为30°和从30°变为45°时，含裂纹损伤钢构件的断后伸长率下降的比例大于1.5%。而从60°变为75°时，含裂纹损伤钢构件的断后伸长率下降的比例小于0.5%。从75°变为90°时，断后伸长率保持不变。当裂纹角度小于60°时，含裂纹损伤钢构件的裂纹角度每增加15°，其断后伸长率下降幅度大于1%。当裂纹角度大于60°时，裂纹角度每增加15°，其断后伸长率依然下降，但是下降幅度很慢，最后趋于平缓。

表2 不同角度断后对应的伸长率Table 2 Elongation after breaking at different angles

如表3和图4所示，分别为裂纹角度一定时，不同相对裂纹长度对应的断后伸长率和试验钢构件断后对比图。

从表3可知，当相对裂纹长度小于0.320时，其断后伸长率下降率大于1%，当对裂纹长度大于0.320时，其断后伸长率下降率降为0.2%。图4从左到右相对裂纹长度逐渐增大，从图4可知，随着相对裂纹长度增大，断后伸长量逐渐减小。

图4 不同相对裂纹长度的断后伸长量(裂纹角度为15°)Fig.4 Elongation after fracture for different crack lengths (crack angle is 15°)

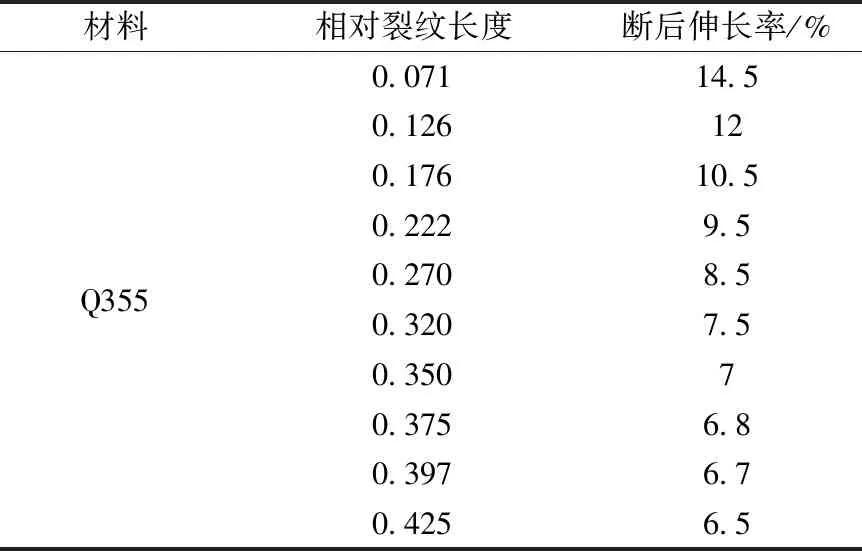
表3 不同相对裂纹长度对应的断后伸长率(Q355)Table 3 Elongation after fracture with different relative crack lengths(Q355)

综上所述，裂纹角度及相对裂纹长度对含裂纹损伤钢构件断后伸长率均有影响，随着相对裂纹长度的增大，含裂纹损伤钢构件的断后伸长率也将减小。因此可以结合裂纹角度及相对裂纹长度考虑对含裂纹损伤钢构件断后伸长率的影响。

表4为Q355钢的含裂纹损伤钢构件在不同裂纹角度，不同相对裂纹长度对其断后伸长率影响汇总。

从表4可知，当裂纹角度为15°和30°时，且相对裂纹长度小于0.270时，相对裂纹长度每增加0.05，其断后伸长率的下降率均大于1%。当裂纹角度为45°、60°、75°和90°时，当相对裂纹长度小于0.176时，相对裂纹长度每增加0.05，断后伸长率下降率均大于1%。在相对裂纹长度为0.222～0.270时，断后伸长率有一个陡降，超过1%，这是由于含裂纹损伤钢构件从塑性破坏转变为脆性破坏了。当相对裂纹长度大于0.375时，含裂纹损伤钢构件完全脆性破坏，断后伸长率仅为2%，且随着相对裂纹长度与裂纹角度增加，断后伸长率保持不变。

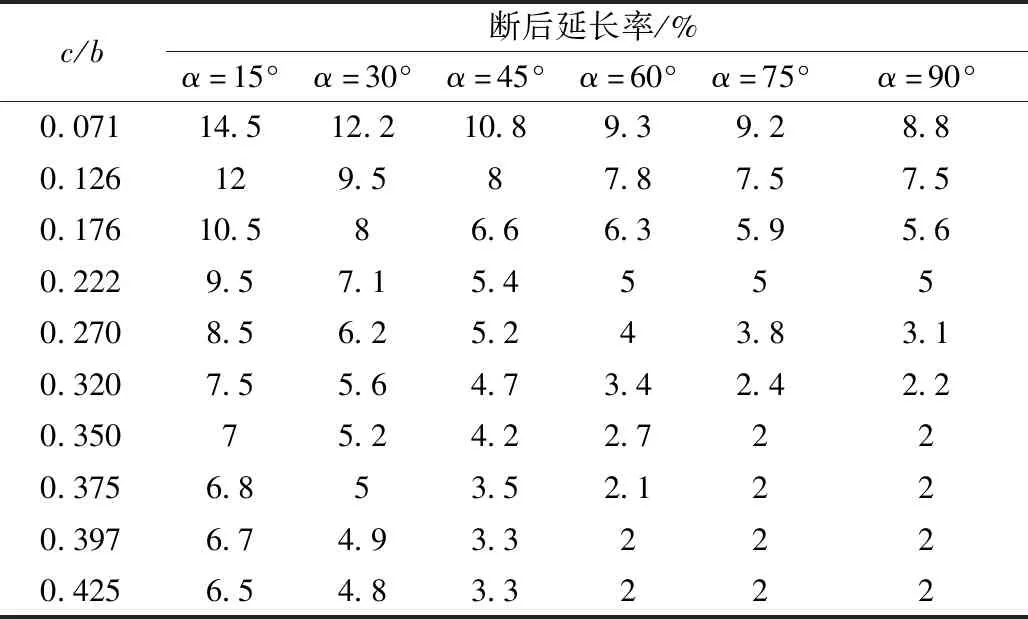
表4 试验构件断后伸长率汇总(Q355)Table 4 Summary of elongation of test member after breaking(Q355)

2.2 Q235和Q355钢的含裂纹损伤钢构件断后伸长率对比

针对Q235和Q355两种不同钢，对其断后伸长率进行试验研究分析，如图5和表5所示。

图5 Q235和Q355钢的断后伸长量(其他条件相同的情况下)Fig.5 Elongation after fracture of Q235 and Q355 steel (under the same other conditions)

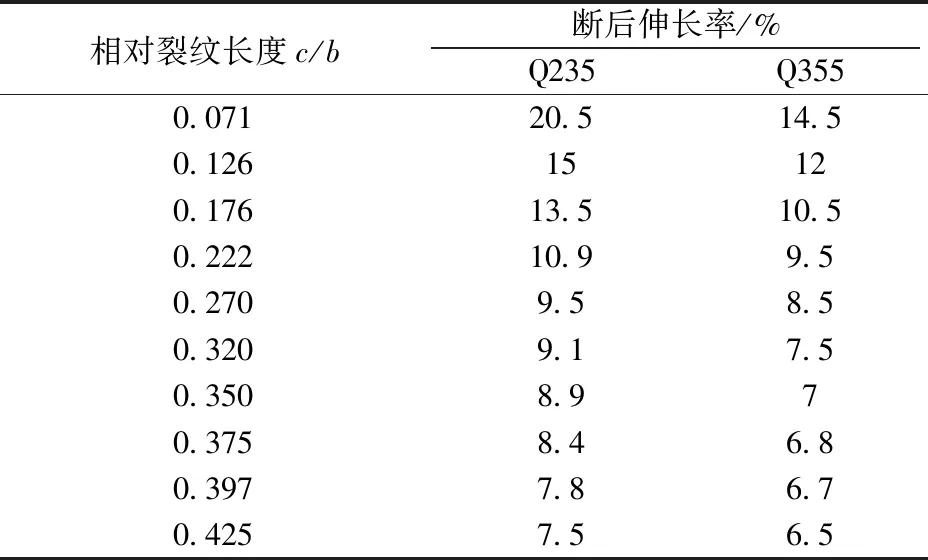
表5 Q235和Q355钢断后伸长率Table 5 Q235 and Q355 steel elongation after fracture

对于Q235和Q355钢的含裂纹损伤钢构件断后伸长率。由图5(标记为Q235钢)和表5可知，Q355钢的断后伸长率普遍小于Q235钢。当相对裂纹长度为0.071时,Q355钢比Q235钢的断后伸长率小6%，当相对裂纹长度为0.425时,Q355钢比Q235钢的断后伸长率小1%。研究发现，无论是否存在裂纹，钢构件的屈强比越大，其断后伸长率越小。由于Q235钢的屈强比小于Q355钢的屈强比，因此，Q355钢的断后伸长率普遍小于Q235钢。

2.3 Q235和Q355钢的含裂纹损伤钢构件材料性能

通过分析试验结果，Q235和Q355钢的含裂纹损伤钢构件破坏形式如表6、表7所示。

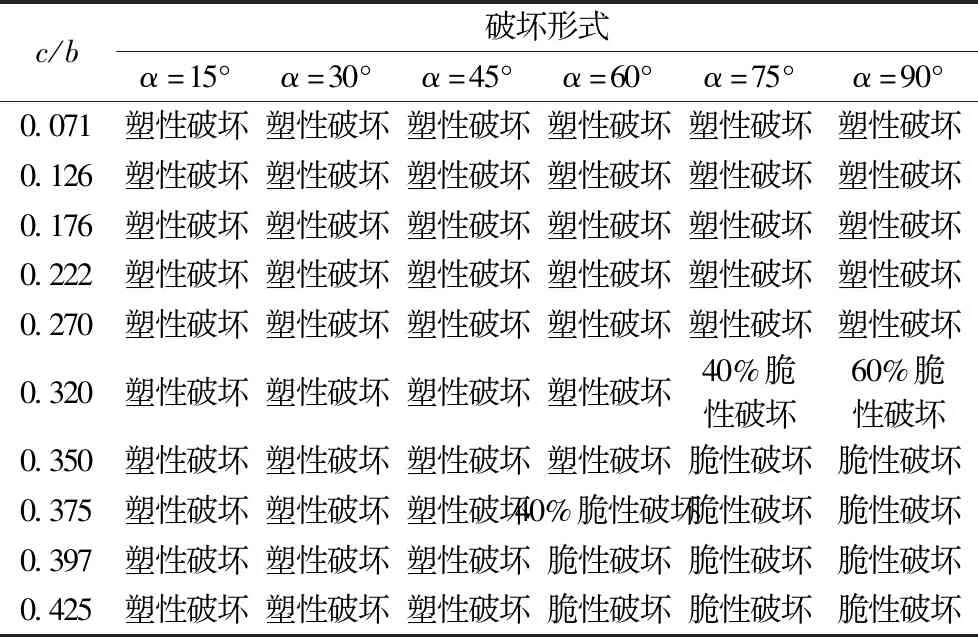
表6 Q235试验构件的试验破坏形式汇总Table 6 The summary of test result of test damage model

从表6、表7可知，含裂纹损伤钢构件的裂纹长度及角度的增加均会导致其出现脆性破坏的情况增多。以Q235钢的含裂纹损伤钢构件为例，在裂纹角度为15°、30°和45°时，含裂纹损伤钢构件均呈现塑性性能，破坏形式为塑性破坏。裂纹角度60°时，当相对裂纹长度为0.375时，有40%钢构件呈现脆性性能，破坏形式为脆性破坏。当相对裂纹长度大于0.375时，均呈现脆性性能，为脆性破坏。

屈强比反映了钢材的安全可靠程度，材料屈强比越大，塑性储能越小。反之，屈强比越小，塑性储能越大，安全性更高。从表6、表7，还可以对比Q235和Q355钢的含裂纹损伤钢构件的破坏形式。以裂纹角度45°为例，当相对裂纹长度为0.350时，Q235钢构件全部表现为塑性破坏，而Q355钢构件有60%表现为脆性破坏。研究发现，无论是否存在裂纹，屈强比大的钢构件比例极限越大，降低了其塑性储能，更容易出现脆性破坏。因此，在其他条件相同时，含裂纹损伤钢构件中，Q235钢比Q355钢呈现脆性性能的情况更少，出现脆性破坏的现象更少。

3 屈强比和裂纹角度的变化对钢构件性能的影响研究

3.1 投影法

根据试验数据，含裂纹损伤钢构件屈服强度数据如表8所示(以15°、45°、75°和90°为例)。

根据表8可知，含裂纹损伤钢构件在90°裂纹情况下，相对裂纹长度与屈服强度的关系，如图6所示。

从图6可以发现，随着相对裂纹长度的增加，含裂纹损伤钢构件的屈服强度是逐渐衰减的，且呈近似线性衰减。

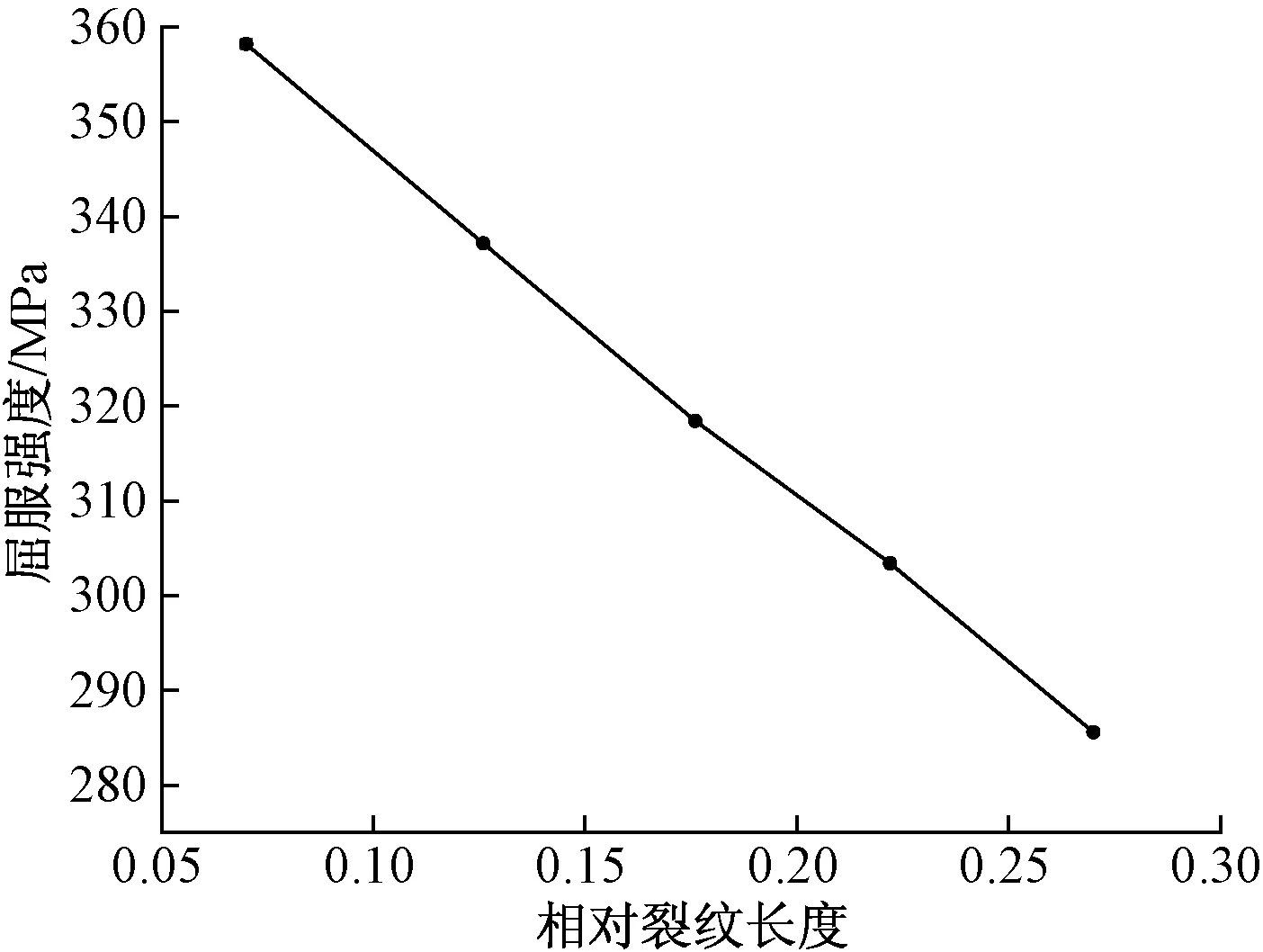
图6 屈服强度与相对裂纹长度关系图(90°)Fig.6 Relation diagram of residual ultimate strength and relative crack length(90°)

对于不同角度的裂纹，通过表8数据可知不同角度的含裂纹损伤钢构件屈服强度与相对裂纹长度的关系，如图7所示。

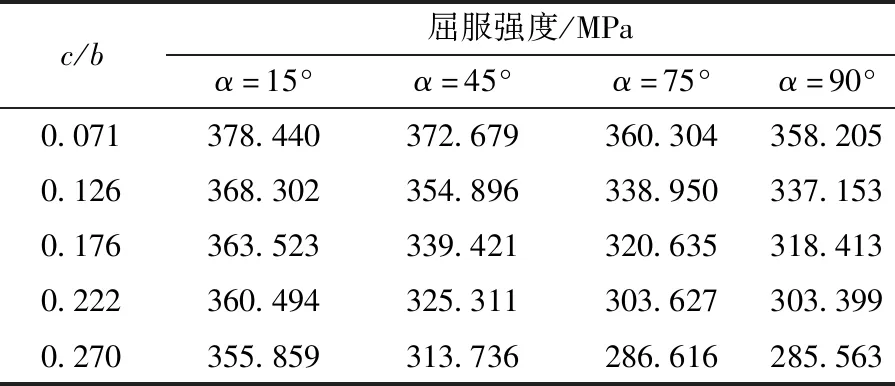
表8 Q355试验构件屈服强度Table 8 Q355 residual ultimate strength of test member

从图7可以看出，不同角度裂纹的相对长度对屈服强度的影响是呈现近似线性衰减的。考虑裂纹角度对屈服强度的影响，可以通过投影法将裂纹角度为α的裂纹转化为与受力方向垂直的裂纹(角度为90°)来处理，如图8所示。

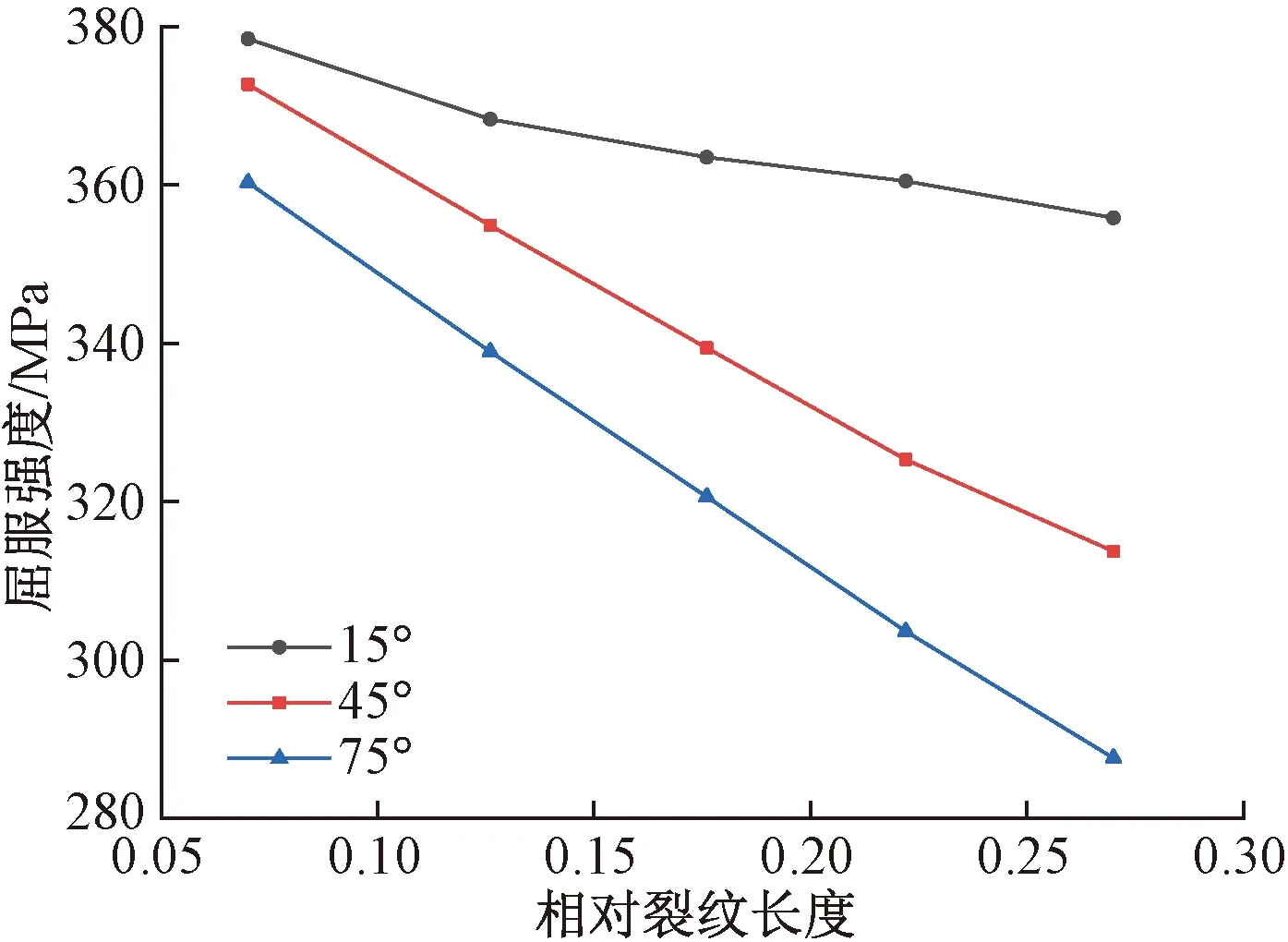
图7 屈服强度与相对裂纹长度关系图Fig.7 Relation diagram of residual ultimate strength and relative crack length

如图8所示，可以得到不同角度的裂纹转化为与受力方向垂直的裂纹(角度为90°)后的投影后相对裂纹长度，如表9所示。

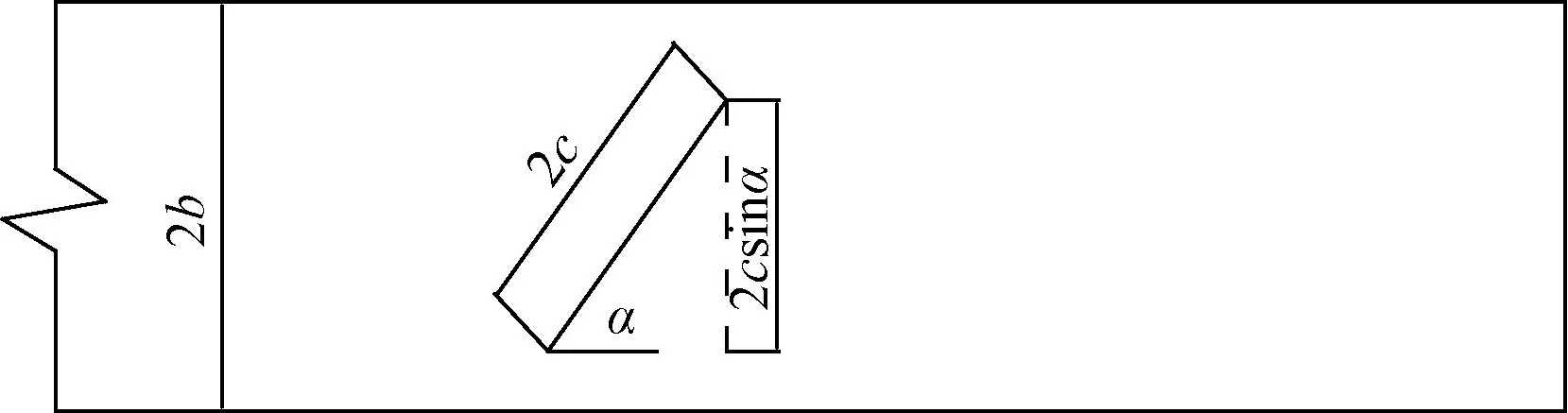
图8 投影法示意图Fig.8 Schematic diagram of projection method

根据表9，拟合出屈服强度与相对裂纹长度的关系，如图9所示。

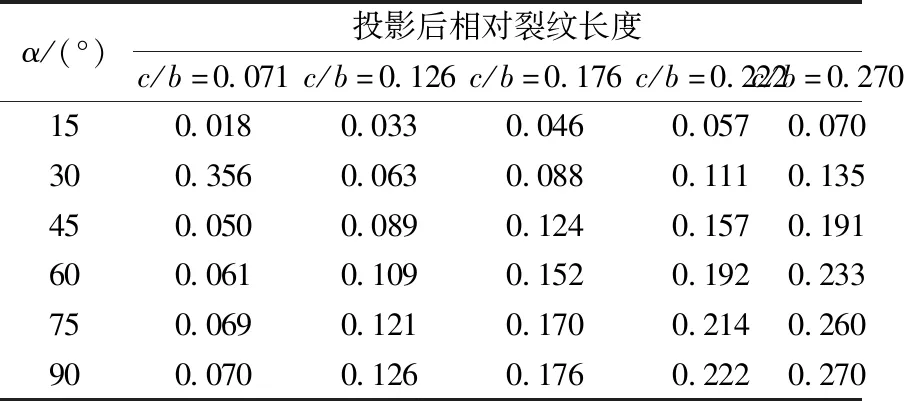
表9 投影后的相对裂纹长度Table 9 Relative crack length after projection

从图9可以发现，相对裂纹长度与屈服强度拟合效果良好，证明了投影法的可行性。因此，可以得到不同裂纹角度的相对裂纹长度转化为与受力方向垂直的裂纹(角度为90°)的投影后相对裂纹长度公式为

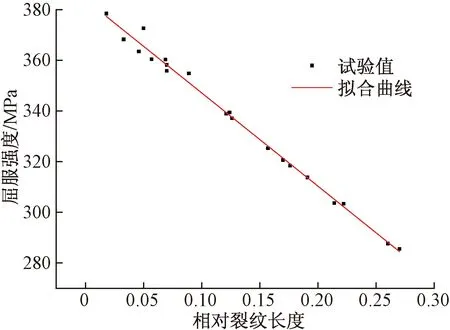
图9 屈服强度与相对裂纹长度关系示意图Fig.9 Schematic diagram of residual ultimate strength and relative crack length

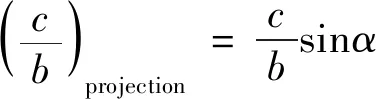
(1)

3.2 改进后的剩余极限强度公式

研究发现，随着相对裂纹长度的增大，含裂纹损伤钢构件由于裂纹的存在容易造成局部应力集中，从而降低钢构件的极限承载能力。当裂纹存在时，研究人员把含裂纹损伤钢构件能够承受的极限应力称为其剩余极限强度。试验发现含裂纹损伤钢构件的屈服强度同样随着相对裂纹长度的增加而减小，因此，将试验测得的屈服强度与有限元公式计算的剩余极限强度理论值[12]对比如表10所示。

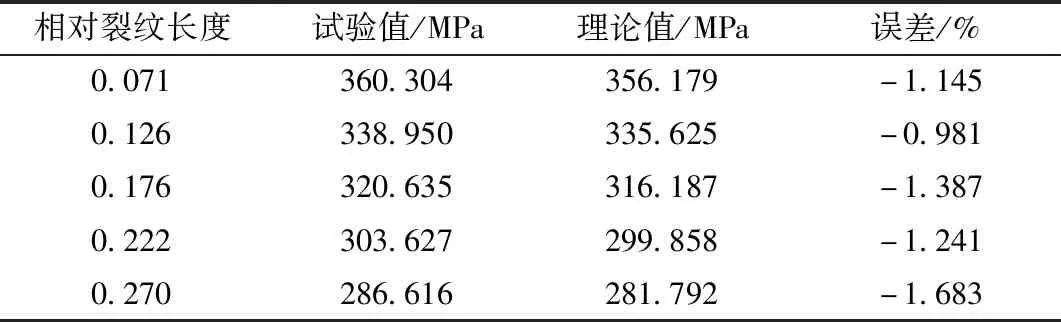
表10 试验值与有限元公式对比Table 10 Comparison of test value and finite element formula

通过对比试验值与有限元公式计算值，可以发现误差较小，因此假定含裂纹损伤钢构件的剩余极限强度可以当作钢材的屈服强度来处理。但是，随着相对裂纹长度的增大，有限元公式计算的剩余极限强度与试验值误差逐渐增大。这是由于该理论计算公式中所用的屈强比是一个定值，没有考虑到屈强比会随着相对裂纹长度的改变而变化。

研究发现，相对裂纹长度对含裂纹损伤钢构件的屈服强度σs和极限强度σb均有影响，并且随着相对裂纹长度增大，含裂纹损伤钢构件屈强比会增大，如表11所示。

从表11可以发现，相对裂纹长度对含裂纹损伤钢构件的屈强比影响较大，在相对裂纹长度为0.071时，屈强比为0.744 5，在相对裂纹长度为0.270时，屈强比为0.764 4。随着相对裂纹长度的增大，含裂纹损伤钢构件的屈强比呈现逐渐增大的趋势。

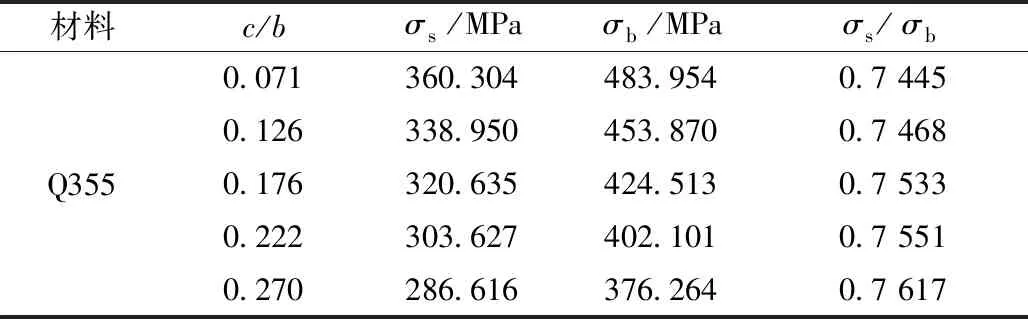
表11 不同相对裂纹长度钢构件的屈强比Table 11 Yield ratio of steel members with different relative crack lengths

研究可知，含裂纹损伤钢构件剩余极限强度和抗拉极限强度均随相对裂纹长度的增大而减小，且都呈近似线性减小，因此其屈强比也将呈现近似线性变化，故可以将含裂纹损伤钢构件的屈强比与相对裂纹长度进行线性拟合，如图10所示。

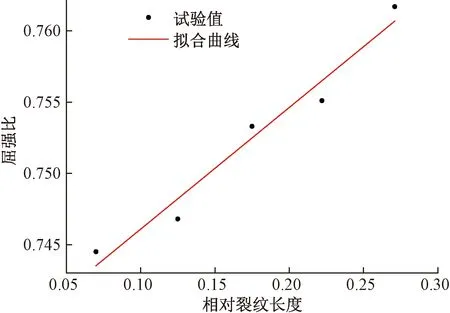
图10 屈强比与相对裂纹长度关系图Fig.10 Relation diagram of yield ratio and relative crack length

从图10可知，随着相对裂纹长度的增大，含裂纹损伤钢构件的屈强比逐渐增大。结合试验可以拟合出较为简单的含裂纹损伤钢构件的屈强比随着相对裂纹长度增大的关系，可表示为

(2)

因此考虑屈强比随着相对裂纹长度的变化，结合有限元计算公式以及式(2)可以得到改进的剩余极限强度公式为

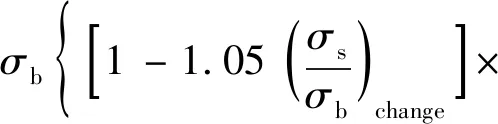
(3)

通过所提出的投影法，可以得到不同角度下含裂纹损伤钢构件剩余极限强度公式为

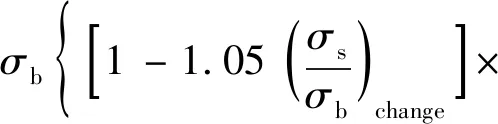
(4)

将式(4)所计算的剩余极限强度与试验值以及有限元公式计算值对比，如表12和图11所示。

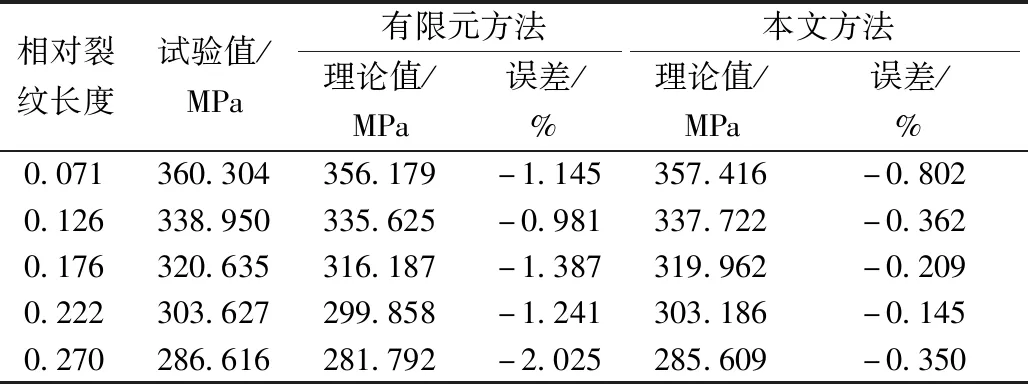
表12 试验值与两种方法公式计算值对比Table 12 Comparison of test values and two method formulas

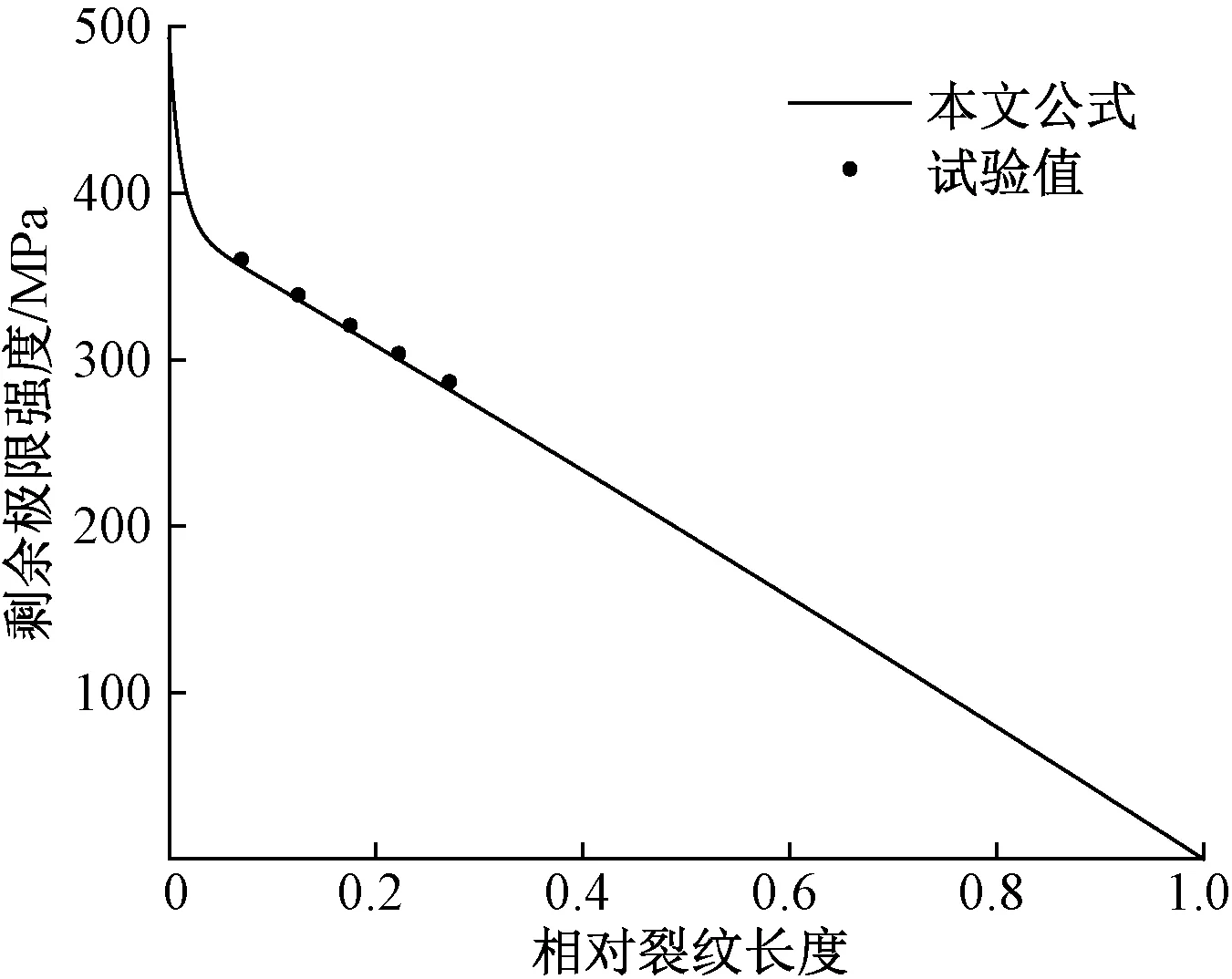
图11 试验值与本文公式计算值对比Fig.11 Comparison of test value and two method formulas

对比表12和图11可以发现，改进后的剩余极限强度公式更为精确，更为贴近实际试验值。改进后的公式计算值与试验值相比误差小于1%，并且随着相对裂纹长度的增大并没有出现误差明显增大的情况，证明了改进后的剩余极限强度公式的准确性。

4 结论

针对Q235和Q355两种不同钢材分别考虑不同裂纹角度和不同相对裂纹长度的情况下开展拉伸试验，分析了其断后伸长率、剩余极限强度和破坏形式，得到以下结论。

(1)对于含裂纹损伤钢构件，在相对裂纹长度为0.071，裂纹角度为15°时，其断后伸长率最大可达20.5%；当相对裂纹长度小于0.222时，相对裂纹长度每增加0.05，含裂纹损伤钢构件断后伸长率下降幅度大于1%。相对裂纹长度为0.350，裂纹角度为90°时，断后伸长率最小为2%。当相对裂纹长度大于0.350时，断后伸长率基本保持2%不变。对于Q235钢的含裂纹损伤钢构件，当相对裂纹长度为0.309时，40%钢构件呈现脆性性能。Q355钢的含裂纹损伤钢构件，当相对裂纹长度为0.233时，20%钢构件呈现脆性性能。

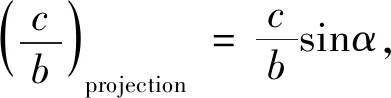
(3)随着相对裂纹长度增加，屈强比发生改变。给出了更为精确的剩余极限强度公式，将试验值与公式计算值的误差减小至1%。