螺旋桨气动/噪声多目标优化设计

薛东文 ， 刘兴强 ， 燕群 ， 陈永辉

(1. 航空工业飞机强度研究所， 西安 710065； 2. 航空声学与振动航空科技重点实验室， 西安 710065)

螺旋桨是飞机最早期的动力装置，近些年来，学术和工业界对其关注度越来越高。主要原因是：现今阶段通用无人机发展越来越成熟，而通用无人机的推进装置为螺旋桨[1]；石油资源日益枯竭，绿色电动飞机的研究成为热点，而螺旋桨是电动飞机的主要动力；短程通用航空以及轻质运动飞机[2]的动力源也是螺旋桨。

目前制约飞机螺旋桨广泛应用的瓶颈是其噪声问题。螺旋桨飞机的主要噪声来自于螺旋桨和发动机。降低螺旋桨飞机发动机噪声可通过设计合适的喷口或者换装电机来解决。而对于螺旋桨气动噪声来讲，降低其噪声辐射的唯一途径是改变其桨叶形状。

不同于涡扇发动机的短舱声衬降噪，螺旋桨桨叶的低噪声设计必然与其气动性能密切相关，很多情况下螺旋桨性能和低噪声是相互冲突的两个参数。螺旋桨的低噪声设计通常需要应用多目标优化方法开展。

多目标优化算法可以考虑多重约束，且能够很好的取得螺旋桨性能和噪声之间的折中。现如今，多目标优化算法已经广泛应用于螺旋桨的气动和噪声优化设计。法国宇航院在ANIBAL项目下针对某轻型螺旋桨飞机开展了螺旋桨多目标优化设计[3]，应用升力线方法计算螺旋桨气动性能，应用FW-H方法计算气动噪声。由于该方法基于升力线理论，对螺旋桨气动噪声有重要影响的弦长、安装角等参数没有充分考虑在内，优化得到的螺旋桨沿展向无扭转角变化。Ohad[4-5]、Daniel等[6]、Huang等[7]应用多学科优化方法针对某无人机螺旋桨开展多学科优化设计，其所基于的气动性能计算方法是动量-叶素理论。该方法假定螺旋桨气流无径向流动，桨叶之间无相互干扰，因而无法精确的预测螺旋桨气动性能。而螺旋桨的气动性能预测直接给定用于气动噪声源计算的气动力分布，精度较差的气动性能计算方法将影响螺旋桨气动/噪声优化目标的实现。Burger等[8]应用更为精确的涡格法计算螺旋桨气动性能，应用半经验模型计算气动噪声[8]，没有考虑对螺旋桨噪声影响较为严重的“弯”这一参数。目前，计算流体力学(computational fluid dynamics, CFD)的方法也大量的用于螺旋桨气动性能计算，该方法能够相对全面的考虑螺旋桨几何参数，但计算速度低于动量-叶素理论、升力线方法和涡格方法2个数量级，导致优化效率偏低。例如，Marinus等[9-10]基于RANS和FW-H方法研究了多目标优化设计，以弦长、安装角等参数为设计变量，没有考虑“弯”，甚至没有考虑“掠”；宋翔等[11]研究了螺旋桨气动与噪声的多目标优化问题。该工作已安装角和弦长为设计变量，忽略了其他与气动噪声相关的变量，如弯、掠。闫文辉等[12]开展了倾转旋翼飞机的旋翼流动和噪声分析，没有对螺旋桨开展设计。可以看出，目前螺旋桨气动/噪声多目标优化设计存在的问题是气动性能计算精度偏低(升力线和动量-叶素理论)、计算效率(计算流体力学方法计算效率偏低)和所考虑的设计变量种类不足，因而对螺旋桨的优化尚不全面。

基于升力面方法[13]计算螺旋桨气动性能，耦合Hanson螺旋桨频域计算方法[14]，开展螺旋桨远场噪声预测，以期实现螺旋桨气动与噪声的精确预测。应用多目标优化方法，以螺旋桨沿叶高分布的弦长、安装角、弯和掠为设计变量，以气动性能和远场噪声为优化目标，开展某大尺寸螺旋桨的气动与噪声的多目标优化设计，以期实现全面的螺旋桨气动噪声优化设计。针对最优桨叶开展高精度数值计算方法的验算，验证精确的高效、全面优化方法的准确性。

1 螺旋桨气动性能计算方法与验证

1.1 螺旋桨气动性能计算方法

沿桨叶中弧面布设等环量的四边形涡环，由最后的环脱出螺旋形马蹄涡，一直延伸到下游无穷远，形成常值半径的螺旋形尾迹(在螺旋桨为轻载的情况下，可以近似地假设尾涡无收缩，每一条螺旋马蹄涡为等螺距和等直径。这个假设与Goldstein的假设是一致的)。由整个螺旋桨涡系引起的诱导速度用Biot-Savart定理计算，通过在控制点上满足物面边界条件可以确定桨叶上的环量分布。有了环量以后，根据Kutta-Jourkowski关系式可以求得每一微段涡元的升力，在考虑截面阻力以后，可以求得螺旋桨的拉力系数CT，功率系数CP及螺旋桨效率η[6]。

虽然基于涡格法的升力面方法在计算诱导速度时用的仍是不可压流的Biot-Savart，但在计算作用力时，如采用高速时翼型的气动特性数据，仍可用于计算高速螺旋桨的性能。实际算例表明，在飞行马赫数Ma达0.7时，计算结果仍与实验数据吻合尚好[15]。

四边形涡环和螺旋形马蹄涡的诱导速度可按升力线理论中的类似公式计算。如序号为(I，J)的涡环在序号为(m，n)的控制点处的诱导速度计算公式为

(1)

式(1)中：umn、vmn、wmn为三个方向的诱导速度；v∞为来流速度；R为螺旋桨半径；ΓIJ为涡格环量；FuIJmn、FvIJmn、FwIJmn为序号为(I，J)的涡格对序号为(m，n)的涡格在三个方向的诱导系数。

边界条件为在物面上垂直物面的速度分量为零，可以得到

(2)

由每个控制点的方程(2)组成了线性方程组，可以得到每个控制点上的ΓIJ/4πRv∞的值。有了ΓIJ/4πRv∞后，按同样的方法可求得控制点上的诱导速度，加上来流速度和旋转速度，得到总速度。由Kutta-Joukowski关系式求每涡元所受的力，并考虑带压缩性正的翼型阻力系数Cd和升力系数CL可以求得螺旋桨气动性能。

1.2 螺旋桨气动性能计算方法的验证

NACA6623-A螺旋桨是一种直叶桨。NASA曾于20世纪做过一系列气动性能试验，可用于本文应用的气动性能计算方法的研制[16]。

在用升力面的分析中，将桨叶沿展向(轮毂至桨尖)均分为20等份，沿弦向进行保角变换处理，即前、尾缘加密，分为15份。由此在桨叶表面形成20×15个四边形涡格。尾涡的积分间距为0.022 2 rad，积分长度8π rad。

图1、图2分别给出了在不同75%安装角、不同进速比下螺旋桨功率系数和推力系数计算结果与试验结果的对比。可以看出，总体上在不同进速比下、不同安装角下计算结果与试验结果相近。升力面理论特别适用于较高进速比下的螺旋桨气动性能预计。

图1 螺旋桨功率系数计算验证Fig.1 Propeller power coefficient calculation verification

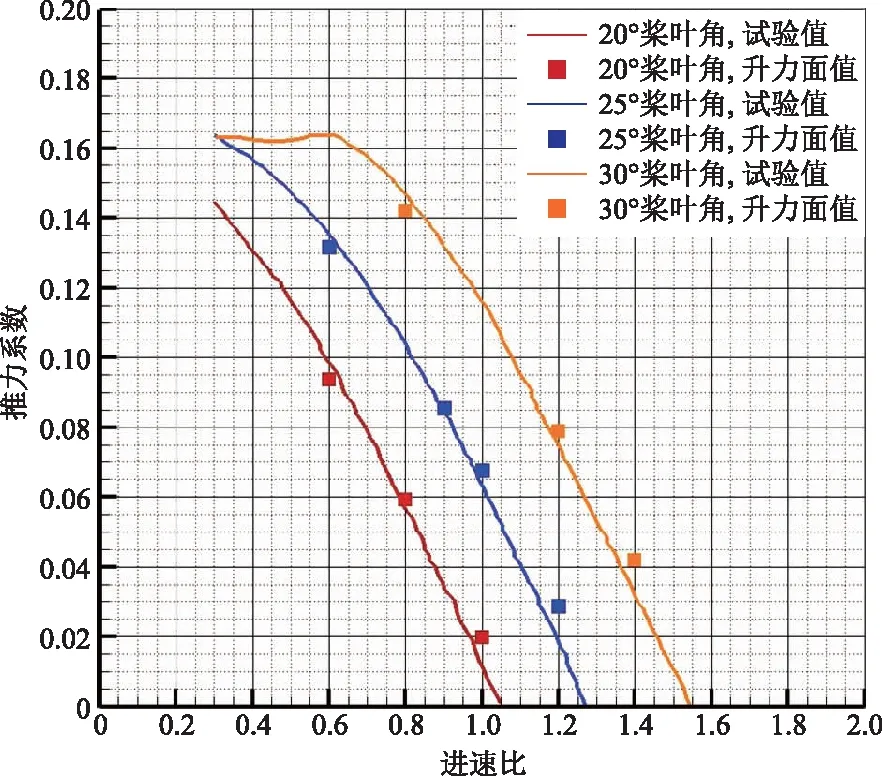
图2 螺旋桨推力系数计算验证Fig.2 Propeller thrust coefficient calculation verification

2 螺旋桨气动噪声性能计算方法

Herniczek等[17-18]，通过与多个模型实验结果对比，研究了不同螺旋桨噪声模型的预测精度。结果表明在预测纯音噪声时，Hanson噪声模型的计算方式相对于其他早期噪声理论，多个算例与实验的平均误差最小，具有较高的计算精度。

螺旋桨产生的声压扰动可以表示为厚度噪声、载荷噪声和四极子噪声三项之和，即

c0ρ′(x,t)=pT(x,t)+pL(x,t)+pQ(x,t)

(3)

根据Hanson频域噪声计算方法[12]，厚度噪声可写为

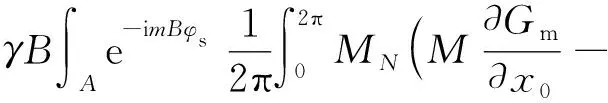
(4)

载荷噪声表示为

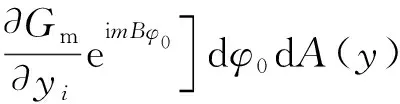
(5)

式(5)中：c0为背景声速；B为桨叶数；m为谐波数；γ为比热比，声源坐标为y=(y1，y2，y3)；vN表示物面相对于流体的法向速度；vNdAdt表示面积元素dA在时间增量内的体积位移；Gm为格林函数。MN=vN/c0，km=mBMt，Mt=ΩR/c0;φ0为桨叶旋转后的周向角度；φs为面元所在的相位角。根据升力面方法求解螺旋桨气动性能可以给出式(5)所需的面积单元上的叶片载荷fidA。

由此，将螺旋桨气动性能与气动噪声性能联合可获得特定工况下给定气动外形的螺旋桨气动和气动噪声特性。

四极子噪声不是空气螺旋桨的主要噪声源，在这里忽略。

3 设计变量、优化方法与优化目标

3.1 设计变量的选取

在螺旋桨的气动与噪声设计中，设计变量通常可分为3类：通用设计变量、桨叶设计变量、横截面(翼型)设计变量。通用设计变量影响了螺旋桨系统的整体结构，通常包括：螺旋桨/发动机数目、桨叶数目、螺旋桨半径、螺旋桨转速。桨叶设计变量是用来确定螺旋桨的每片桨叶的几何与结构，通常包括：安装角、弦长；前/后掠角、左/右弯角。横截面(翼型)设计变量直接定义了翼型的几何形状。

影响螺旋桨气动与噪声特性的最主要参数是沿桨叶高度方向的扭转角分布、弦长分布和叶尖形状。由不同叶高位置的翼型、翼型的弦长、翼型的安装角/扭转角、弯、掠可唯一的确定螺旋桨的中弧面，由此，可由基于涡格法的不考虑厚度的升力面理论得到螺旋桨桨叶表面的力的分布和螺旋桨气动性能(推力、效率等)。而在螺旋桨的气动噪声分量中，载荷噪声是螺旋桨噪声的最主要分量，厚度噪声占比很小，在计算结果的总噪声中，厚度噪声的影响甚至小于0.5 dB，可以忽略。此外桨叶厚度本身是对螺旋桨结构强度的保证，本文重点开展螺旋桨的气动与噪声性能优化设计，保持桨叶厚度不变可一定程度上不改变桨叶的结构强度性能。桨叶厚度分布不作为优化设计变量。

在本文中，不考虑原始螺旋桨的翼型形状，应用ARA-D翼型，优化设计的变量类型包括：沿叶高分布的弦长、安装角、弯和掠，共4类变量。

3.2 设计变量的参数化

当叶型截面较多时，直接以各个叶型上的弦长、安装角、弯、掠为设计变量，会造成较大的计算量，当相邻叶型的参数该变量较大时会影响桨叶的光顺性，过于激进的桨叶外形不利于飞行演示验证。因此，在本项目中对桨叶做参数化处理，即，将4类设计变量沿叶高的变化拟合为参数曲线(Bezier曲线)，取有限个截面的4类参数作为设计变量。基本逻辑如图3所示。

图3 叶型参数化示意[19]Fig.3 Leaf shape parameterization diagram

从桨尖至叶根沿桨叶高度均布4个叶型截面。为保证装配，叶根无弯；向旋转方向的方向弯；最大值为桨叶半径的2%(过大的弯不利于桨叶结构强度)。

以轮毂外壳以上的桨叶区域作为优化设计区域，保证桨叶与轮毂的安装方式不变化。

从桨尖至叶根沿桨叶高度均布4个叶型截面。为保证装配，叶根部弦长与原始桨保持一致，且该位置的弦长不作为设计变量。

3.3 设计变量的约束

从桨尖至叶根沿桨叶高度均布4个叶型截面。为保证装配，叶根部安装角与原始桨保持一致，不作为设计变量。其他3个位置的安装角作为设计变量。最大安装角靠近叶根位置；最小安装角在桨尖，保证桨尖的攻角为正值。

为保证装配，根部无掠；桨叶底部前掠，桨尖后掠；考虑到过大的掠不利于桨叶结构强度，最大值为桨叶半径的4%。

为保证装配，叶根无弯；向旋转方向的方向弯；最大值为桨叶半径的2%(过大的弯不利于桨叶结构强度)。

3.4 优化方法

遗传算法是以自然选择和遗传理论为基础，将生物进化过程中适者生存规则与群体内部染色体的随机信息交换机制相结合的高效全局寻优搜索算法。它将问题域中的可能解看作是群体的一个个体或染色体，对群体反复进行基于遗传学的操作(遗传、交叉和变异)。它在很多领域都有广泛的应用，特别是对于一些非线性、多模型、多目标的函数优化问题，用其他优化方法较难求解，而遗传算法可以方便地得到较好的结果。

本文中应用了英国谢菲尔德大学的遗传算法代码，应用的优化设计变量有12个。设置优化种群尺度为360，最大进化代数取500(多次优化表明，大约400步找到最优解)，交叉概率取0.9，变异概率取0.05，离散精度取0.01。

为了加速迭代，采用了并行算法，用12个核同步计算同一种群的不同个体。

为了避免遗传算法基因之间的离散性带来的设计变量突变而导致的俄桨叶锯齿状问题，叶型参数化中应用了Bezier曲线拟合。

为了避免得到的结果是过早收敛的结果，作者进行了多轮优化，确认优化得到的是同一个螺旋桨外形。

3.5 优化目标的设定

本文优化设计的目标是在不降低螺旋桨气动性能的前提下降低螺旋桨远场辐射噪声。由此引出了3个优化目标：螺旋桨气动效率、螺旋桨推力、螺旋桨远场辐射噪声。噪声观测点为远场旋转平面处测点。

以线性加权和法处理多个优化目标之间的关系，而加权因子需要反复尝试，使得既能够降低桨叶的气动噪声，又能够保证螺旋桨气动性能不损失并满足螺旋桨结构强度性能。表达式为

(6)

将它的最优解x*作为目标函数在线性加权和意义下的“最优解”，其中ωi为加权因子。

4 优化对象及工况

优化对象为某大型无人机螺旋桨。该螺旋桨为3叶推力桨，螺旋桨直径为1.87 m。

来流速度40 m/s，螺旋桨旋转速度2 058 r/min。

5 优化结果

5.1 优化过程与收敛的判定

在优化过程中发现：

(1)螺旋桨拉力改变量小于0.01 N。

(2)螺旋桨效率改变量小于0.00 1。

(3)螺旋桨气动噪声该变量小于0.01 dB。

因此，可以优化已经收敛。优化前后螺旋桨推力和效率以及螺旋桨旋转平面处的气动噪声对比如表1所示。可以看到，螺旋桨的气动性能没有改变，而螺旋桨1 阶叶片通过频率(blade pass frequency, BPF)远场峰值噪声降低5 dB。

表1 优化前/后螺旋桨气动与噪声的对比Table 1 Optimize the comparison of aerodynamics and noise of the front/rear propellers

5.2 优化结果

优化得到的弦长分布如图4所示。可以看出相比原始桨，优化桨的弦长在小于35%叶根区域更大，而在桨叶中部和桨尖区域，优化桨的弦长更大。可以猜想，在不改变桨叶推力的同时，降低噪声，那可以通过在更大的弦长范围内分布载荷，使得桨叶表面的压力梯度降低，从而实现噪声载荷的降低。

优化得到的安装角分布如图5所示。相比原始桨，优化桨的安装角在65%以下的桨叶截面，安装角更小；而在65%以上，优化桨的安装角更小。因此，可以理解为，更多的65%以下的桨叶承担的气动载荷增加，而65%以上的气动载荷降低。噪声载荷通常在桨尖位置，通过这种气动载荷的转移进一步实现噪声载荷的降低。

优化得到的掠分布如图6所示。基本上程序桨叶的下半部分前掠，后半部分后掠的形态。通过改变沿桨叶叶高的气动噪声载荷的相位，实现远场噪声抵消。

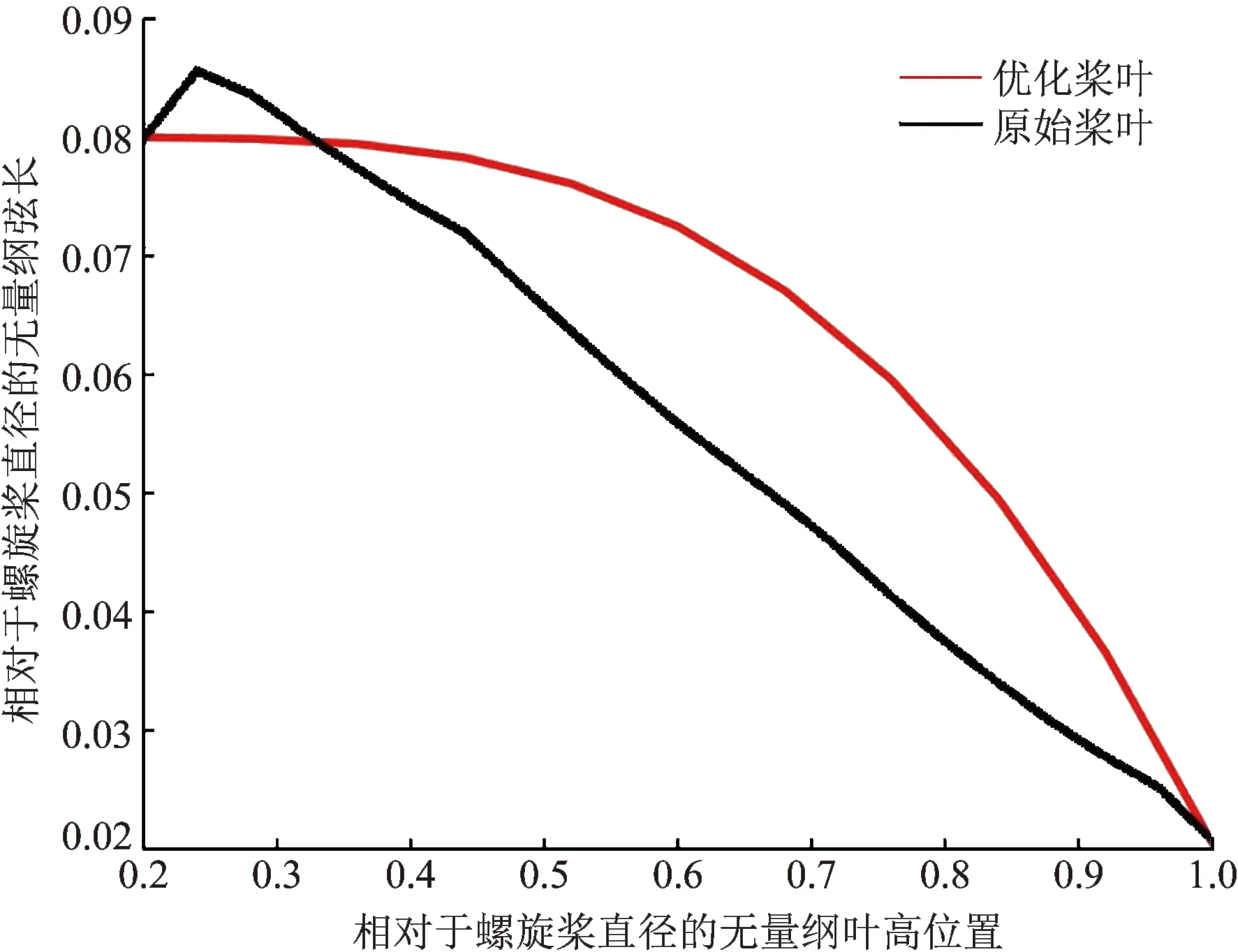
图4 弦长分布Fig.4 Chord distribution

图5 安装角分布Fig.5 Installation angle distribution

图6 掠分布Fig.6 Sweep distribution

优化得到的弯分布如图7所示，基本上程序桨叶的下半部分左弯，后半部分右弯的形态。类似于桨叶掠设计，通过改变沿桨叶叶高的气动噪声载荷的相位，实现远场噪声抵消。

优化桨与原始桨的整体对比如图8所示。可以看出，相比于原始桨，优化桨的弦长明显增大，有明显的掠特征。

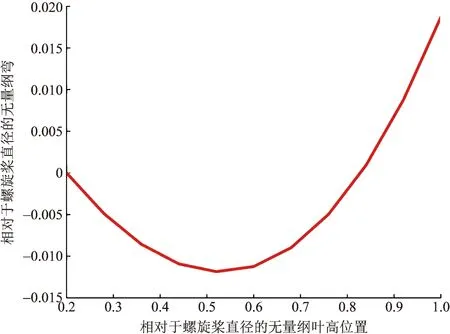
图7 弯分布Fig.7 Bend distribution

图8 原始-优化桨叶对比Fig.8 Original-optimized blade comparison

6 优化结果的数值验证

6.1 气动计算方法

采用的主控方程为N-S方程，湍流模型为S-A模型。

在计算网格方面，计算域为上游5D，下游10D(D为螺旋桨直径)。桨叶近体网格采用六面体结构网格，首层网格y+=15，生长率1.1，结构网格层数50层。桨叶脱体网格采用多面体网格。总网格量1 200万，核心区800万网格，如图9、图10所示。

在边界条件的设置方面，旋转域采用多重参考坐标系，近场为无滑移壁面，远场采用压力远场边界，气体为理想气体，采用海平面密度，离散格式为二阶迎风。

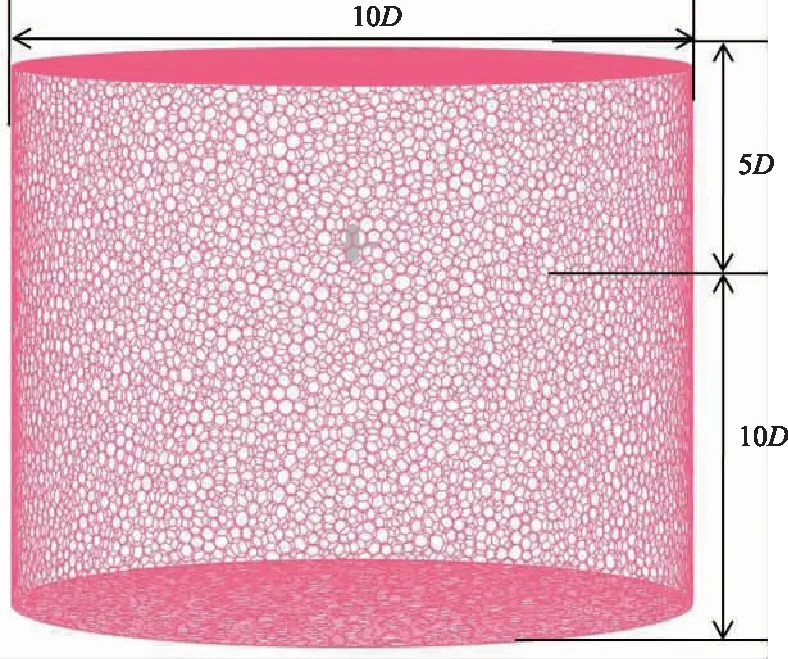
图9 CFD计算域Fig.9 CFD computational domain

图10 螺旋桨均布网格Fig.10 Propeller uniformly distributed grid

6.2 气动计算方法的验证

根据风洞试验的科目，完成了四个工况的原始桨气动计算，如表2所示。定常计算得到的不同工况的推力系数与试验比非常接近，误差均小于3%。说明本文所用的数值计算方法精度较高。

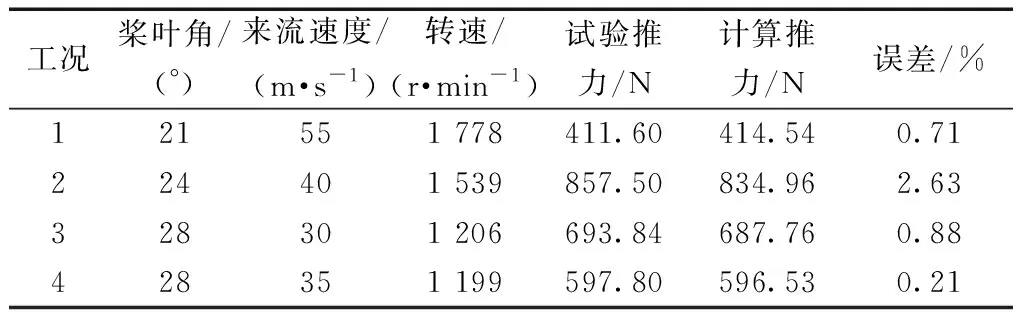
表2 计算工况与推力计算误差Table 2 Calculation conditions and thrust calculation errors

6.3 气动噪声计算方法

通过气体动力学计算获得桨叶表面的载荷分布，进一步应用Hanson频域方法获得桨叶表面的声源分布，最后，应用声学有限元组合无限元积分的方法计算噪声在远场的分布。

声学计算域如图11所示，红色区域是螺旋桨所在的旋转区域，包含了主要的噪声源；声传播有限元区域采用半径分别为0.3 m和1.2 m的椭圆区域；无限元积分面是最外围的椭圆积分面。

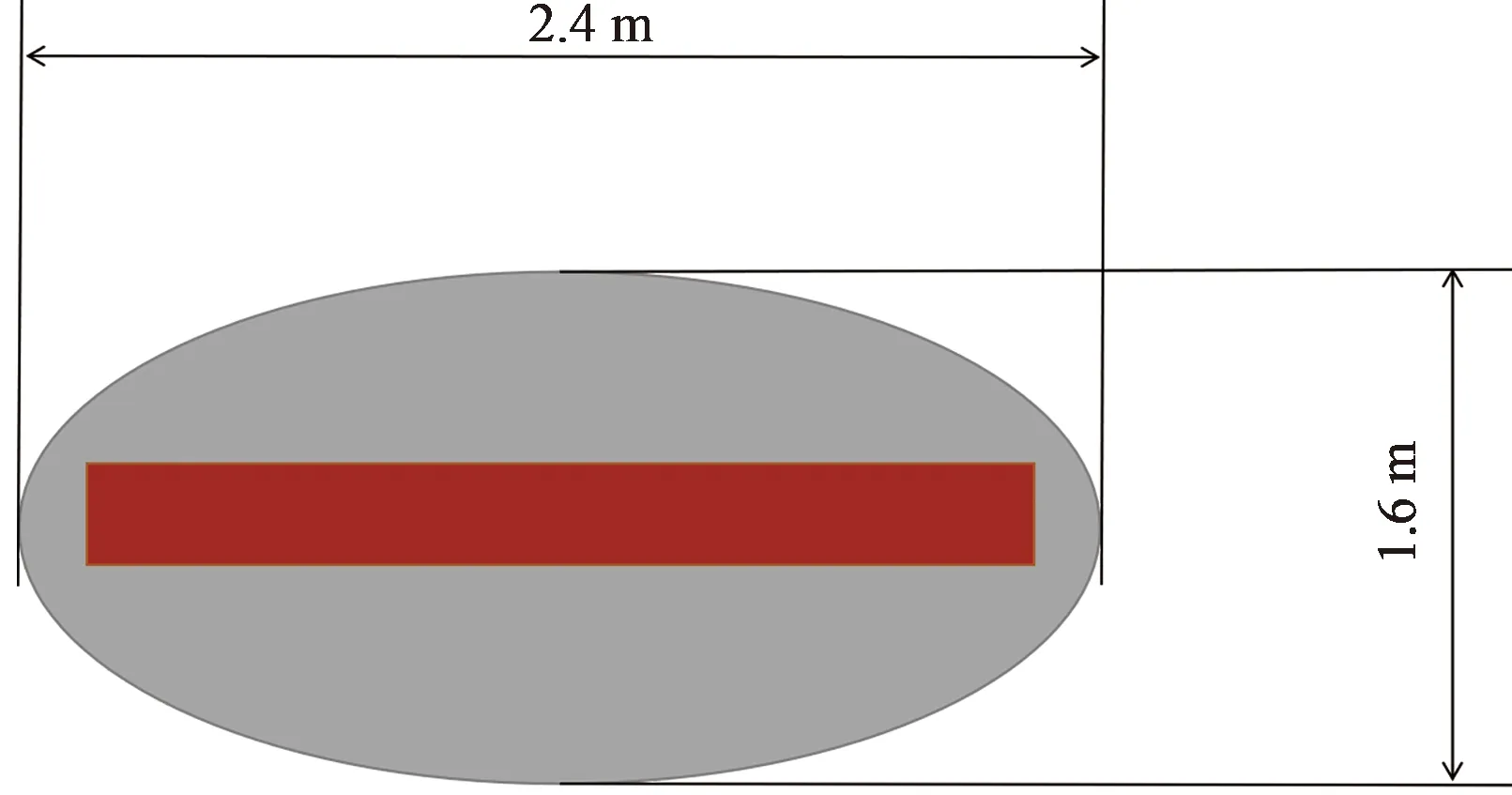
图11 计算气动声学计算域Fig.11 Computational aeroacoustics calculation domain

6.4 计算结果

6.4.1 气动性能对比分析

优化前、后的螺旋桨的推力-扭矩-效率对比如表3所示，优化桨的推力和扭矩较原始桨均有所增大；优化桨的效率与原始桨相当。

数值计算的推力、效率与半解析计算方法的推力、效率非常接近，说明了半解析方法在计算螺旋桨气动性能方面的精度较高。

6.4.2 气动噪声性能对比分析

图12为第一阶BPF远场指向性对比曲线，载荷噪声呈现为典型的偶极子指向性，最大噪声在旋转平面附近，优化桨较原始桨在最大噪声位置降低5 dB。

图13为第二阶噪声对比曲线，优化桨较原始桨降低约3 dB。图14是第三阶噪声对比曲线，优桨与原始桨叶有所降低。

可以看出，对于1 BPF在螺旋桨旋转平面上的噪声，应用数值方法的计算结果与应用解析方法的计算结果数值相近，降噪量评估近似，具有相同的结论。

表3 优化前/后螺旋桨气动性能对比Table 3 Optimize the comparison of the aerodynamic performance of the front/rear propellers

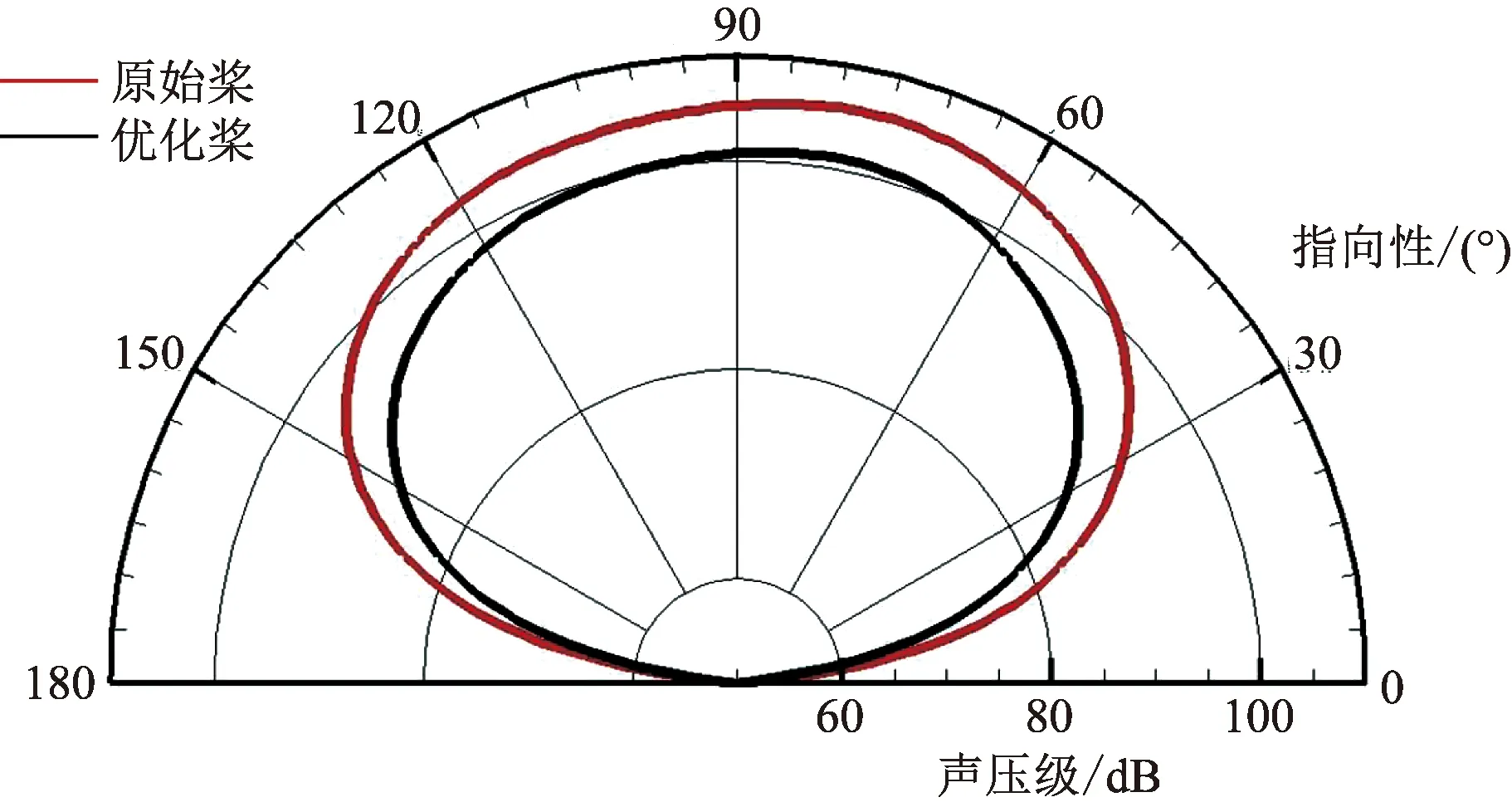
图12 第一阶噪声对比曲线Fig.12 Noise contrast curve at 1BPF

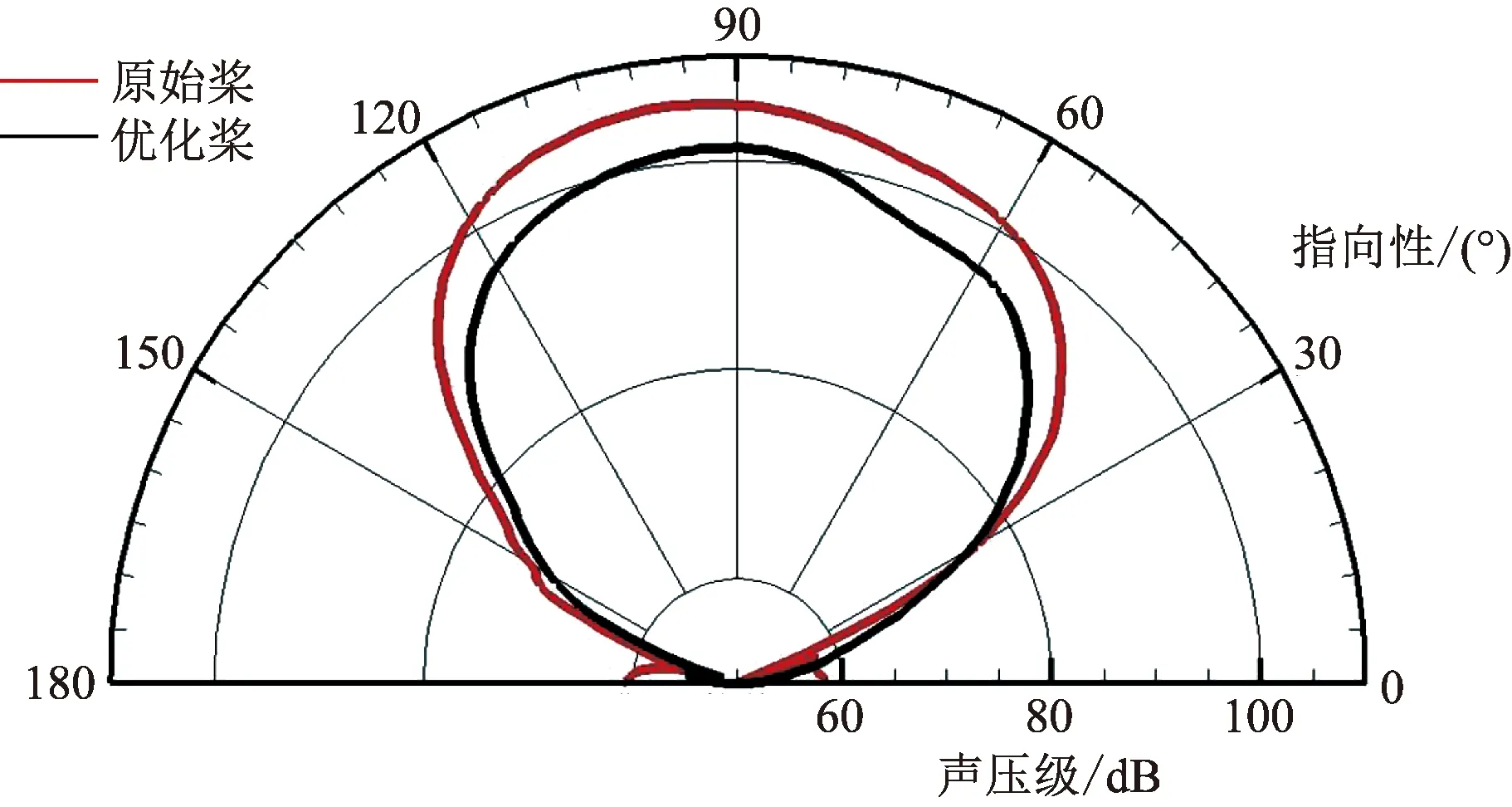
图13 第二阶噪声对比曲线Fig.13 Noise contrast curve at 2BPF

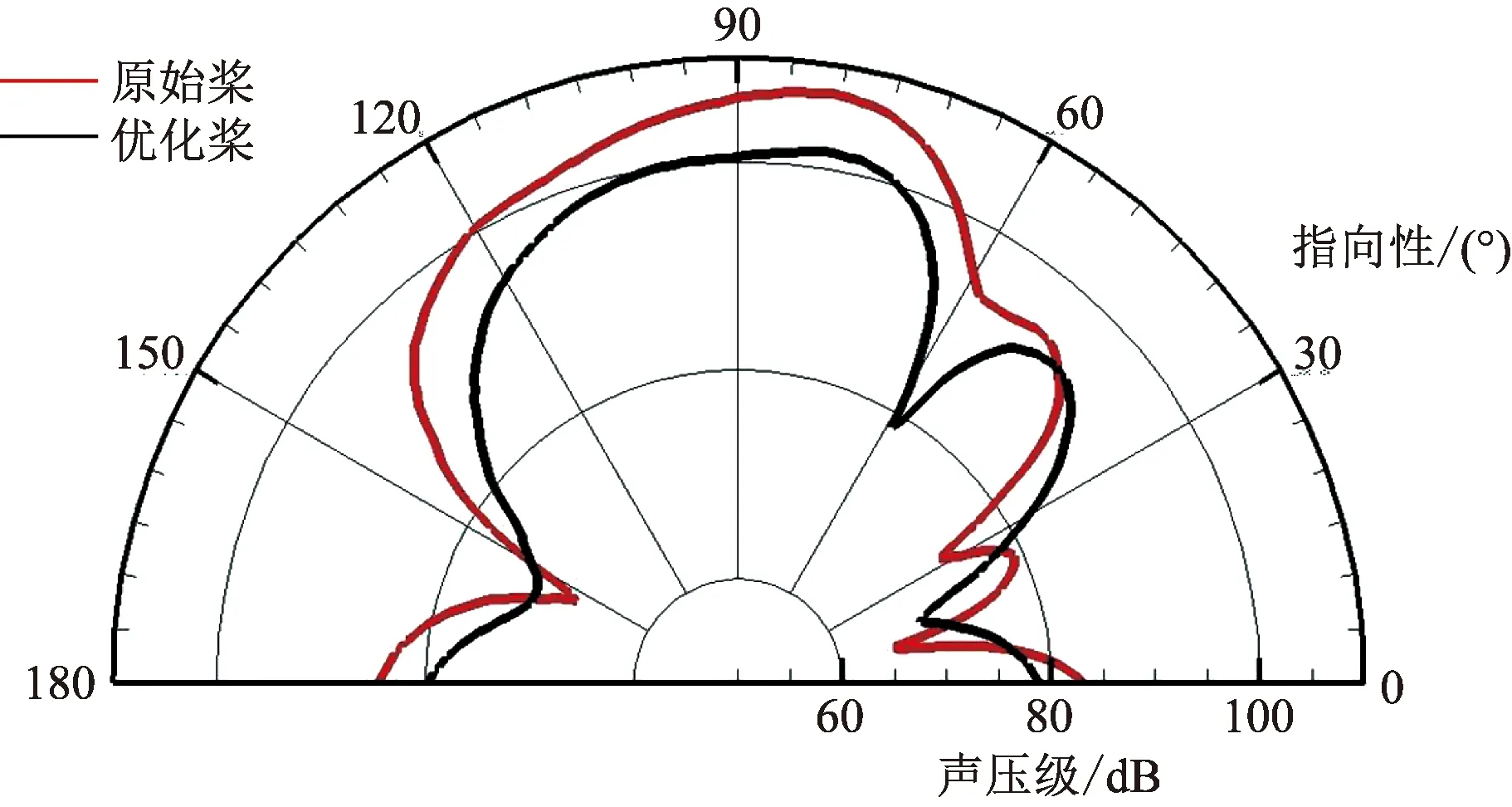
图14 第三阶噪声对比曲线Fig.14 Noise contrast curve at 3BPF

7 结论

针对某大尺寸螺旋桨开展气动与噪声联合优化设计,得到如下主要结论。

(1)基于升力面理论与Hanson频域远场噪声计算方法，开展了螺旋桨气动性能的计算与远场噪声评估，通过试验验证了计算精度和适用范围。

(2)以螺旋桨桨叶沿展向分布的弦长、安装角、弯、掠为设计变量，不改变螺旋桨桨叶数、半径和转速的情况下，以螺旋桨气动性能不降低和远场噪声降低为优化目标，开展螺旋桨的气动与噪声联合优化设计。优化结果表明，在不降低螺旋桨气动性能的情况下，优化设计的螺旋桨桨叶的1阶气动噪声降低5 dB，在2阶和3阶叶片通过频率处仍有降噪效果。

(3)通过数值仿真方法验证了优化结果的正确性，两种方法在对原始桨和优化桨的气动性能和气动噪声的预计方面，推力和效率均吻合，气动噪声量级相等。验证了本文给出了螺旋桨气动与噪声优化方法的适用性。