粗糙裂缝对井眼声波传播的影响

曹鸿飞， 章成广*， 蔡明， 陈义群， 蔡德洋

(1．长江大学， 油气资源与勘探技术教育部重点实验室， 武汉 430100; 2．中石油塔里木油田分公司勘探开发研究院， 库尔勒 841000)

随着中外石油天然气工业的迅猛发展和油气勘探的逐渐深入，常规油气产量日渐减少，目前，非常规储层具有越来越广阔的勘探开发前景。中外有关致密储层的研究表明，由于致密砂岩储层的脆性较强，裂缝在致密砂岩储层中普遍存在且往往比较发育，在裂缝性致密砂岩储层中，裂缝不仅作为流通油气的通道，而且有储存和渗透油气的作用，裂缝的研究、评价和预测成为了研究人员的关注重点[1-11]。利用现有的常规测井数据很难精确地评价裂缝性致密储层，特殊测井资料评价裂缝的方法也各有缺陷，例如，声、电成像测井测量范围较窄，不能准确地反映出井外裂缝的延伸。阵列声波测井技术虽可以克服成像测井评价方法的缺陷，但由于裂缝性致密储层的裂缝的复杂性和裂缝位置的不确定性，使裂缝地层对阵列声波波形的干扰增大[12]。由于地层中的裂缝常具有高角度和粗糙性等复杂特征，利用现有的阵列声波测井技术和成像测井技术对地层中的裂缝进行定量地精细评价具有重要的实际意义[9,13]。

斯通利波是一种比井内流体声速稍低的低频散导波，具有低频率、高能量和高振幅的特征。当地层中裂缝与井孔相交时，由于地层中的泥浆会和地层中的液体互相流通，从而使斯通利波能量流失，并在非连续界面上产生反射和衰减[14]。在阵列声波测井中，由于斯通利波反射系数对裂缝性地层中的裂缝宽度具有较高的灵敏度[15]，因此可以用斯通利波对裂缝进行识别和分析。许多学者利用多种方法研究了不同裂缝因素对斯通利波传播影响的研究。Ou等[16]通过有限差分的方法研究水平裂缝的斯通利波反射，在多个模型中模拟了斯通利波的传播，说明了利用斯通利波检测裂缝的可行性。杨博等[17]通过水槽实验得到裂缝张开度和斯通利波幅度衰减系数之间的关系，结合由阵列声波测井资料得到的斯通利波衰减系数，计算裂缝张开度，并反演得到裂缝渗透率。刘黎等[18]利用倾斜裂缝地层模型和岩心实验研究了斯通利波穿过倾斜光滑裂缝时的响应情况。Li等[19]研究了裂缝宽度、倾角和裂缝充填物等因素对斯通利波传播的影响。

上述学者所研究的裂缝都为光滑裂缝，由于裂缝壁面的粗糙性会使测井裂缝评价结果和实际产生偏差，为了减小因裂缝的粗糙性造成的误差，有必要对粗糙裂缝进行研究。粗糙裂缝的粗糙性相对难以量化，常用的二维和三维表面粗糙度表征方法，分为统计，分形和方向特征[20]。中外学者用多种方法对粗糙裂缝进行构建和描述，Brown等[21]通过分形维数、均方根粗糙度和描述两个裂缝面之间不匹配程度的长度来描述粗糙裂缝，建立了一种岩石粗糙裂缝的数学模型。曲冠政等[22]利用三维扫描原理，计算裂缝的迂曲度、倾角、粗糙度等特征参数，模拟了页岩粗糙裂缝中流体的渗流。李大奇等[23]通过调整分形理论产生粗糙裂缝面和裂缝基准面之间的位置来描述粗糙裂缝的缝宽分布，从而构建粗糙裂缝。彭娇等[24]对裂缝结构进行分析，通过采用渗流速度描述裂缝结构中流体渗流的迂曲度计算公式，用于描述裂缝的粗糙性。都凯等[25]运用节理粗糙度系数(joint roughness coefficient，JRC)来计算粗糙裂缝渗透率。Ban等[26]用表征岩石表面局部和整体特征的两个粗糙度参数来替代裂缝粗糙度。上述有关粗糙裂缝的研究大多集中在粗糙裂缝的描述和渗流方面，在测井裂缝评价结果中的应用较少，由于地层中存在粗糙裂缝，研究粗糙裂缝对阵列声波的影响有利于提高测井裂缝评价结果的精度。

1 实验原理

理想全波列波形包括纵波、横波和斯通利波。首先是纵波先到达，其波速最快。其次是横波，横波波速低于纵波而大于斯通利波，其振幅受地层影响较大。斯通利波是一种井筒波，波速比纵、横波速度低，频率比纵波频率小，井眼环境对斯通利波的振幅影响比较大：在规则的井眼环境中，斯通利波振幅远大于纵波和横波；在扩径的井眼环境中，斯通利波振幅会根据扩径的程度的改变而变小。全波列波形经过裂缝后的波形发生变化，当声波经过裂缝时，全波列的振幅衰减非常明显。本文实验主要研究斯通利波和横波的衰减。实验中斯通利波是由单极源低频激发产生，由单级接收器接收记录，其频率范围在3～200 kHz。

在数据分析时利用衰减系数对全波列波形经过裂缝后波形发生的变化进行描述。通过提取横波、斯通利波的幅度，用来计算衰减系数α[17,27-28]，计算公式为

(1)

式(1)中：A0为没有裂缝时读取的斯通利波幅度，mV；A为裂缝存在时读取的斯通利波幅度，mV；l为源距，m。

2 具有不同粗糙度裂缝模型实验

2.1 模型井裂缝粗糙度实验

模型井是根据真实地层的特征加工而成，用于模拟实际储集层中复杂的地质特征[29]，能系统地研究井眼周围的裂缝和地层孔隙度等地质特征对测井结果的影响。

在实验室研究中，通常根据相似理论，将井孔和换能器的尺寸缩小一定倍数(5倍)，而声源频率提高5倍，来模拟实际井中弹性波的传播。与声系尺寸相比，实际井的深度可以看作是无限的，井壁地层厚度也可视为无限。模型井的井壁厚度设计主要取决于声波的探测深度的大小。在单极子声波测井中，纵波的探测深度与声系源距有关，当源距为3～4 in(1 in=25.4 mm)时，声速探测深度为3～4 in，即10 cm左右。因此，可近似地认为，在井壁层厚度至少为15 cm的模拟井中，在短源距的条件下，可以测得斯通利波的传播速度。

根据以上分析，实验设定模型井长、宽、高都为40 cm，井孔直径为4 cm，如图1所示。

图2为花岗岩平板状裂缝模型，花岗岩的骨架密度为2. 710 5 g/cm3，纵波速度为5 400 m/s，横波速度为2 905 m/s。实验用到的设备有水槽和起吊架、尺子和游标卡尺、手摇式千斤顶、一对60 kHz超声探头、CTS-8077PR超声仪和DS1102E型数字示波器、TST3206动态测试分析仪。

用2块砂岩模型，制作凹凸锯齿状槽，如图3所示，单边刻槽，宽度为2 mm，深度为1 mm。在井孔周围6个波长范围内刻槽，井孔直径为4 cm。测量源距为25 cm。

2.2 模型井实验数据分析

实测数据包括刻槽深度为1 mm，宽度为2 mm，源距为25 cm，频率探头为60 kHz。对实测数据进行分析，得到裂缝宽度与斯通利波衰减关系，包括刻槽前后的衰减曲线，如图4所示。

图1 模型井结构Fig.1 Model well structure

图2 平板状裂缝模型Fig.2 Flat crack model

图3 凹凸锯齿状槽模型Fig.3 Concave-convex serrated groove model

将刻槽前和刻槽后的斯通利波衰减少系数进行比较，如图5所示。可以看到，模型井实验的刻槽前和刻槽后的斯通利波斯通利波衰减系数在形态和趋势上很接近。不同的是刻槽后的斯通利波衰减系数相比刻槽前的斯通利波衰减系数有小幅度的增加。这说明了裂缝粗糙度会造成斯通利波幅度衰减，但斯通利波衰减随裂缝宽度的变化关系与平板光滑裂缝相比基本一致。

图4 光滑裂缝和粗糙裂缝的衰减曲线Fig.4 Attenuation curves of smooth cracks and rough cracks with groove

图5 刻槽前、后的斯通利波衰减拟合曲线Fig.5 Fitting curve of stoneley wave attenuation before and after grooving

3 模拟结果验证

3.1 数值模型与算法的实现

图6为平板状裂缝地层井眼模型示意图。模型由井外地层、井眼和水平裂缝组成，裂缝倾角为0°，井眼和裂缝内的填充物为流体，流体波速V=1 500 m/s，密度ρ=1 000 kg/m3。井外地层部分为均匀弹性固体地层，地层纵波速度VP=5 400 m/s，地层横波速度VS=2 905 m/s，地层密度ρ1=2 710.5 kg/m3。地层的外边界采用PML(perfectly matched layer)降低声波反射。井眼半径为0.101 6 m，声源与接收点之间的距离为6英寸。激发声源类型为变形瑞克子波，表达式为

式(2)中:f(t)为幅值，mV；t为时间，s；ω为最大能量频率，rad/s。为了使接收到的斯通利波受纵横波的影响最小，将声源频率设置为2.5 kHz。

为了研究斯通利波穿过裂缝的响应情况，在研究模型的裂缝中采用非均匀的网格对裂缝进行剖分，采用非均匀网格可以在基本不降低计算精度的情况下减小计算量[18]。变网格差分算子在空间分布上具有四阶精度，图7为变网格差分示意图。图7中节点i处的场量ψ对空间的导数∂ψ/∂x可以用4个节点处场量的组合表达式来表示[11]，即

图6 平板状裂缝地层井眼模型示意图Fig.6 Schematic diagram of borehole model in flat fracture formation

图7 变网格差分示意图Fig.7 Variable grid difference schematic

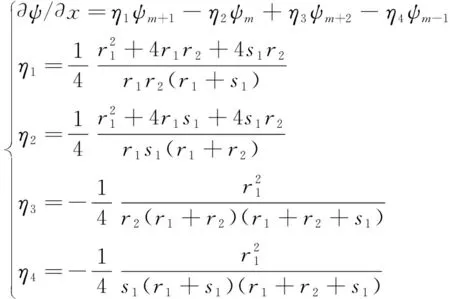
(3)

式(3)为四阶空间精度差分算子在变网格时的表现形式。在网格为均匀时，当s1=r1=r2=Δr时，变网格差分算子改变为具有四阶空间精度均匀网格差分算子，即

(4)

3.2 模拟数据处理

3.2.1 粗糙裂缝模型

在进行物理实验时，在裂缝表面刻凹凸锯齿状方槽，而天然裂缝表面并非是规则凹凸锯齿状方槽，所以在平板状裂缝地层井眼模型的裂缝上下表面制作正弦形状的槽，裂缝上下表面对称，将三维裂缝模型简化为二维截面，如图8所示。

迂曲度即流体实际渗流路径与其视渗流路径的比值，是描述粗糙裂缝结构渗流的一个重要参数[30]，其计算公式为

(5)

式(5)中：τ为迂曲度；L1为流体实际渗流距离，m，在简化的二维模型中L1为弯曲曲线的长度；L0为流体视渗流距离，m；在简化的二维模型中L0为裂缝的长度，如图8所示。对于槽宽L=5 mm，槽深A=2 mm的裂缝，经过计算得到其迂曲度为1.092 4。

3.2.2 粗糙裂缝模型计算

对粗糙裂缝进行数值模拟，图9为槽宽L=5 mm，槽深A=2 mm的粗糙裂缝随宽度变化的波形图，图10为槽宽L=5 mm，槽深A=2 mm的粗糙裂缝的不同裂缝宽度斯通利波幅度衰减与平板光滑裂缝的斯通利波衰减随宽度变化的对比图。可以看出，在裂缝宽度较小时，粗糙裂缝斯通利波的幅度衰减比平板光滑裂缝的斯通利波的幅度衰减明显要小，这主要是因为粗糙的裂缝表面在裂缝宽度较小时明显地降低了裂缝的最小的渗流宽度。

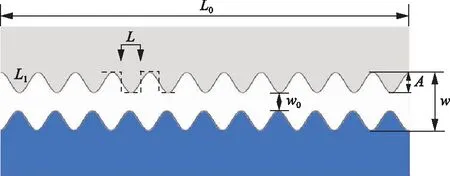
A为槽的深度，L为槽宽，w为粗糙裂缝表面的最大裂缝宽度， w0为粗糙裂缝表面的最小裂缝宽度 图8 粗糙裂缝二维截面Fig.8 Two-dimensional section of rough crack

图9 正弦粗糙的裂缝随宽度变化的波形图Fig.9 Waveform diagram of sinusoidal rough crack changing with width

图10 数值模拟平板光滑裂缝和粗糙裂缝的 斯通利波衰减对比Fig.10 Comparison of stoneley wave attenuation between smooth cracks and rough cracks in numerical simulation plate

3.2.3 迂曲度的影响

对于裂缝表面形如正弦的粗糙裂缝，迂曲度由槽宽和槽深决定。若固定槽深A，改变槽宽L相当于粗糙裂缝的最大宽度和最小宽度不变，改变了最大宽度与最小宽度之间的填充程度。若固定槽宽L，改变槽深A，相当于粗糙裂缝的最大宽度不变，改变了裂缝的最小宽度，最大宽度与最小宽度之间的填充程度的改变不大。这两种情况都会造成迂曲度的改变，下面分别对这两种情况进行分析。

为了研究槽宽L对斯通利波的影响，取裂缝宽度为6、10、16、22 mm，取槽宽L分别为0.5、1、3、5、6、8、10 mm及槽宽为无穷大(相当于光滑裂缝)，槽深为2 mm的4种不同裂缝宽度的粗糙裂缝进行模拟，槽宽越小，迂曲度越大，计算结果用迂曲度表示，如图11所示。可以看到，对于迂曲度的对数lgτ小于0.091 4的裂缝，随着迂曲度的增加，斯通利波的衰减系数减小的速度很快，在迂曲度的对数lgτ大于0.091 4后，斯通利波的衰减系数减小的速度变慢。

当槽宽为无穷小时，lgτ趋于无穷大，相当于裂缝宽度由最大宽度w变为最小宽度w0。对于裂缝宽度为6、10、16、22 mm的粗糙裂缝，当lgτ趋于无穷大时，通过图11的拟合曲线可以计算得到斯通利波衰减系数和斯通利波等效宽度，并在图10中标出，分别对应的点是y1、y2、y3、y4，在图11中可以看到这些点都在对应裂缝的最大、最小宽度之间，可以证明模拟的结果的正确性。

为了研究槽深A对斯通利波的影响，取裂缝宽度为22 mm，取槽深A分别为1、2、3、4、6、8、10 mm，槽宽为5 mm的粗糙裂缝进行模拟，结果如图12所示。结果显示为随着迂曲度的增大，斯通利波的衰减减小，造成这一结果的原因是因为迂曲度的增大，导致裂缝之间的最小的渗流宽度减小，斯通利波的衰减减小。

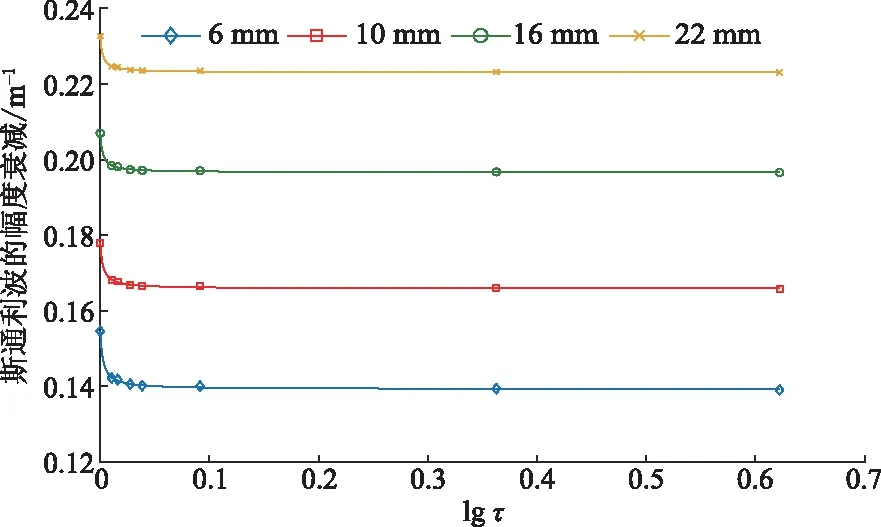
图11 宽为6、10、16、22 mm的裂缝随迂曲度变化的 斯通利波衰减图Fig.11 Stoneley wave attenuation plots of cracks with widths of 6, 10, 16, and 22 mm as a function of tortuosity

图12 宽为22、26、28、30 mm的裂缝随迂 曲度变化的斯通利波衰减图Fig.12 Stoneley wave attenuation plots of fractures with widths of 22, 26, 28, and 30 mm as a function of tortuosity

选取槽宽为5 mm的54组不同的裂缝宽度和不同迂曲度的粗糙裂缝模型进行计算，通过斯通利波衰减系数计算粗糙裂缝的斯通利波等效宽度(表1)。其中，等效裂缝宽度通过斯通利波衰减曲线换算，刻槽后测量的斯通利波衰减值在未刻槽测量的斯通利波衰减曲线上查到对应的横坐标值，这个横坐标值就是对应的等效裂缝宽度。

通过二元拟合建立粗糙裂缝的斯通利波等效宽度与裂缝宽度、迂曲度之间的关系，得到的粗糙裂缝等效宽度计算公式为

w′=6.492-7.261τ+0.749 9w+1.467τ2-0.227 2τw+0.016 63w2，R2=0.999 3

(6)

3.3 与物理模型试验结果对比

选取相同粗糙度的裂缝进行模拟，对于模型井实验中槽宽为2 mm，槽深为1 mm的裂缝，源距选择为25 cm，通过计算得到迂曲度为1.508。在数值模拟时，选取槽宽为5 mm，槽深为5.3 mm的裂缝进行数值模拟，通过计算此时的迂曲度为1.508。将实验数据归一化处理，图13为迂曲度为1.508时的实验和数值模拟的斯通利波衰减拟合曲线。

表1 斯通利波等效宽度和裂缝宽度、迂曲度数据表Table 1 Data table of equivalent width, crack width and tortuosity of stoneley wave

图13 实验和数值模拟的斯通利波衰减拟合曲线Fig.13 Stoneley wave attenuation fitting curve of experiment and numerical simulation

可以看到对于相同迂曲度的粗糙裂缝，实验和模拟的斯通利波衰减系数在形态和趋势上基本一致。

4 结论

裂缝的粗糙性会对声波的响应产生影响，使得计算结果和光滑裂缝的计算结果产生偏差。通过物理实验和数值模拟分别研究了粗糙裂缝对斯通利波响应的影响，得到粗糙裂缝宽度和斯通利波衰减的关系。分别对影响迂曲度的两个参数(槽宽和槽深)进行分析，研究了粗糙裂缝迂曲度、宽度对斯通利波衰减系数的影响，建立斯通利波衰减系数和迂曲度、裂缝宽度之间的关系。通过对实验和数值模拟结果的分析得到以下的结论。

(1)模型井粗糙裂缝实验的结果表明，在探头频率为60 kHz时，光滑裂缝和粗糙裂缝的斯通利波衰减系数和裂缝宽度的关系都为对数关系，粗糙裂缝的斯通利波幅度随裂缝宽度变大而减小，斯通利波衰减系数随裂缝宽度的增大而增大。

(2)对正弦结构粗糙裂缝模型进行数值模拟计算，将得到的裂缝宽度与斯通利波的衰减图和光滑裂缝的结果进行对比，结果显示粗糙裂缝和光滑裂缝的斯通利波衰减系数和裂缝宽度的关系都为对数衰减，不同的是，裂缝的宽度越小，粗糙裂缝和光滑裂缝的斯通利波衰减系数之间的差值越大，造成这一现象的原因是因为槽深不变的情况下随着裂缝宽度的减小，槽深相对于裂缝宽度增大，减小了粗糙裂缝的渗流宽度。

(3)对正弦结构粗糙裂缝模型的数值模拟结果显示，当槽深一定时，槽宽越小，迂曲度越大，随着迂曲度的增加，斯通利波的衰减系数减小的速度由快变慢。当槽宽一定时，槽深越大，迂曲度越大，随着迂曲度的增大，斯通利波的衰减系数减小。