面积与体积共舞，方法与思想齐飞

王定畅

（宁波科学中学 浙江宁波 315336）

一、教学内容分析

本节课选自人教版普通高中教科书第二册第八章第三节，本节课为第二课时。球的体积和表面积公式立体几何中的一个重要的问题，其公式的推导有多种方法，同时也体现了多种重要的数学思想，例如无限分割的思想、类比的思想、极限的思想等等。在这节的教学中，教科书直接给出了球的表面积公式，在这基础上推导球的体积公式。事实上，球的表面积和球的体积公式是存在联系的，因此我们也可以先推导球的体积公式，进而得到球的表面积公式。

因此，本节课的教学重点：①通过类比、极限的思想得到球的体积和表面积的关系。②利用祖暅原理构造模型推导球的体积公式。而该模型的构造也是本节课的教学难点。

二、学习目标分析

1.通过类比圆的面积推导，猜想证明球的体积和表面积的关系。

2.通过祖暅原理和极限分割思想，推导球的体积公式。

三、学生学情分析

在学习这节课之前，学生已经有了用分割的方法推导圆的表面积计算公式的方法和经验，而圆的面积公式的推导本质上是一种“以直代曲”的重要的方法，同时也蕴含着极限这一重要的数学思想。此外，学生刚学习了圆柱和圆锥的体积计算公式，对于圆柱和圆锥的几何结构有了一定的认识，这为之后的祖暅原理的模型构建提供了帮助。

三、教学过程设计

1.回顾旧知，探索新知

教师首先和学生一起回顾圆的面积公式的推导过程，学生掌握的方法是将圆n等分，用该内接正n边形的面积来逼近圆的面积，由此可得：

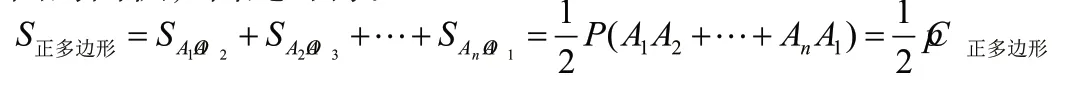
这样便得到了圆的面积和其周长的关系。因此，通过转化就将推导圆的面积公式问题转化为了推导圆的周长公式。这一思想为之后研究球的体积和表面积做了铺垫。

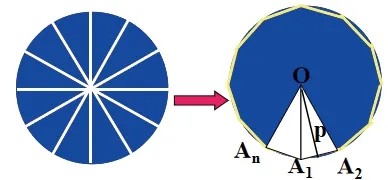
设计意图：从学生现有的知识出发，回顾圆的周长与面积的关系，从而猜想球的表面积和球的体积也具有类似的关系，感受二维和三维空间在处理一些问题时相通的思想方法。事实上，在立体几何的学习和教学中我们经常可以发现，三维空间中的很多结论是二维平面的延伸或推广，因此引导学生如何将一个立体的问题转化为一个平面的问题是非常有必要的。

问题1：类似于将圆n等分，对于球我们又应该如何切割呢？如果可以，能否切割成我们已经学习过的几何体呢？

（学生分小组讨论，并请每个小组派代表分享他们的讨论结果。分割的方法大体分为两

种：将球分割成一些“小椎体”，或者将球分割成“土豆片”）

设计意图：通过提问，瞬间将任务分配给学生，调动学生的思考积极性。由于球的切割方式多种对样，因此每个人可能都会有不同的想法，故在这一教学环节采用的是让学生小组讨论的方式，同时也能活跃课堂气氛。在讨论和展示过程中让学生体验极限分割的思想，从现有的椎体的体积公式来推导球的体积公式，这也符合学生的最近发展区原则。同时，采用小组讨论的形式也能够让每个人都能积极思考，最终取长补短，活跃学生思维。

在各小组讨论的过程中，预设会产生将球分割成如下图所示的几何体。

追问1：如果我们将球分割成如图所示的“小椎体”，那么这些小椎体的体积如何计算？他们的高又是什么呢？

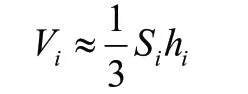
而为了使得近似的体积能够和原几何体的真实体积相差无几，我们只要让分割无限小就可以了，并且此时可将球的半径R近似地作为高ih。

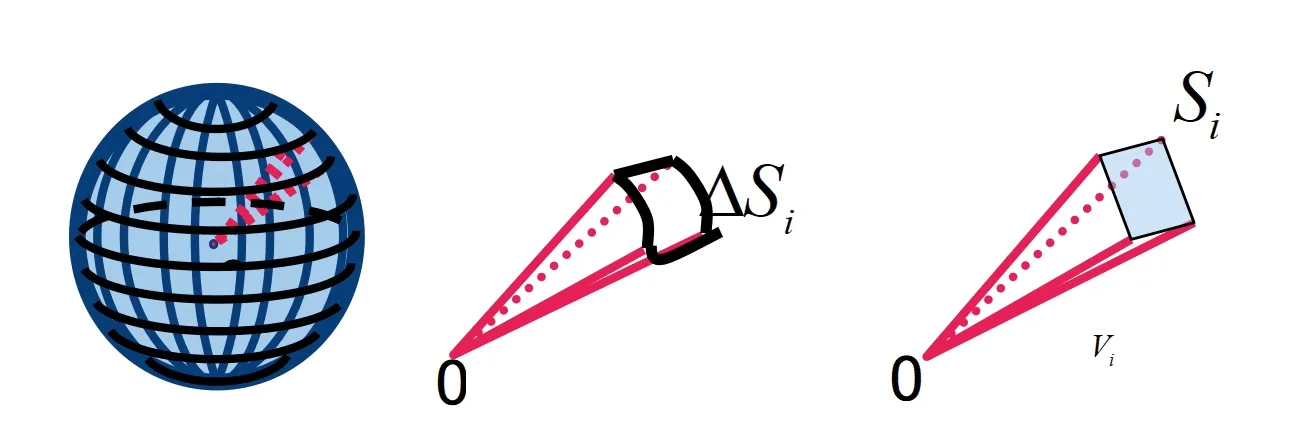
追问2：若将球分割成无数个这样的“小椎体”，那么又可以得到一个什么样的式子呢？

（学生在课堂上独立推导，在这过程中体会感悟体积和表面积关系式的得出）

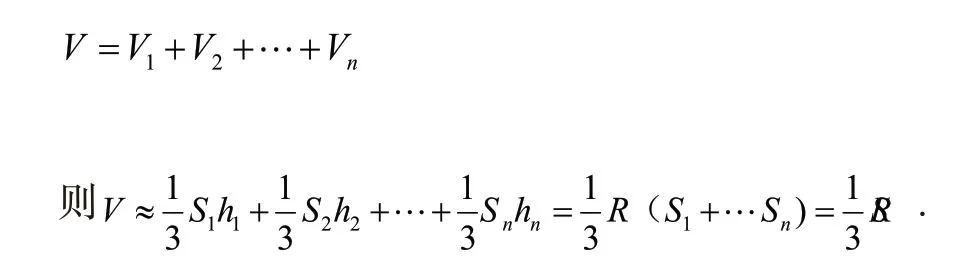
由此得到了球的体积和表面积的关系式。

设计意图：教材中的处理方式是直接给出了球的表面积公式，再利用该关系式得到球的体积计算公式。而实际上通过上述教学过程，我们可以引导学生从极限的思想得到球表面积和体积的关系，通过其他方式先求得球的体积公式，进而便可得到球的表面积公式，不需要直接给出。恰恰相反，如果直接给出球的表面积公式，可能失去了这节课学习的意义，因此设计该教学过程是有意义的。

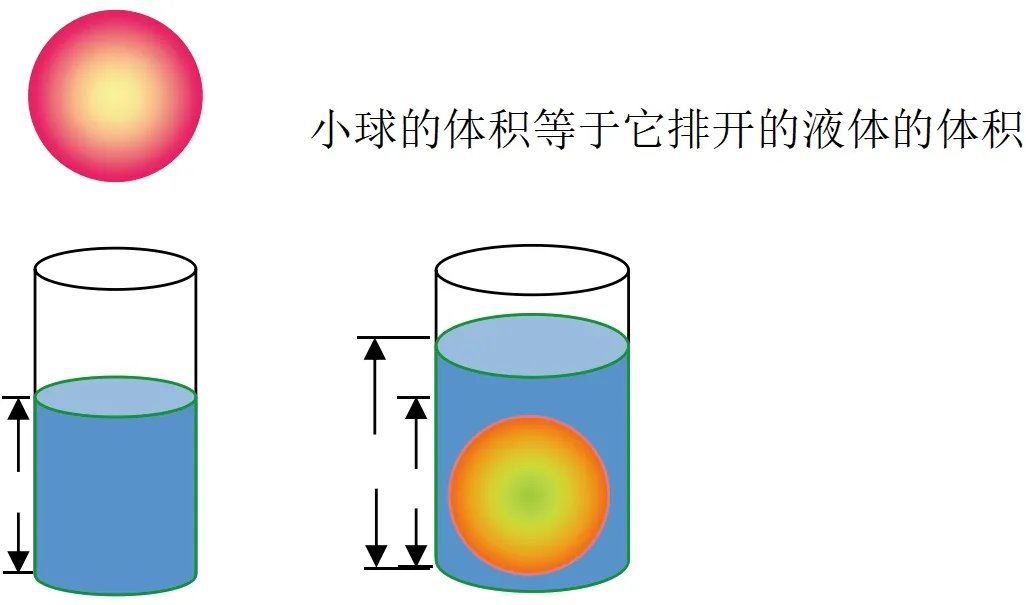
追问3：从等式中我们可以发现，球的体积和表面积公式是有关系的，我们只需要求一个就足够了，那么应该先求球的体积还是表面积呢？

（学生分小组讨论，有的学生可能会提出将球面“拍扁”的方式来推导球的表面积公式，但是很快学生也会发现将球面“拍扁”是不可行的，因此会更倾向于先推导球的体积公式。但是由于缺少一定的理论基础，学生往往会从实际实验的方法出发，比如用阿基米德原理来给出球体积的计算方法，缺少严格的证明）

设计意图：球的体积推导有诸多方法，其中国内比较著名的当属利用祖暅原理。因此通过利用祖暅原理推导球的体积计算公式，能让学生感受到古人的智慧，增强学生的民族自信心和荣誉感，同时也将数学文化渗透到了日常的教学中。

2.构造模型，推导公式

首先可向学生介绍祖暅原理及其由来：祖暅为祖冲之之子，南北朝时取的伟大科学家。祖暅在教师数学上作出了突出贡献，他在实践的基础上，于5世纪末提出了下面的体积计算原理：“幂势既同，则积不容异”。这就是“祖暅原理”。“势”即是高，“幂是面积，祖暅原理用现代语言学可以描述为：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面面积总相等，那么这两个几何体的体积相等。

设计意图：近年来，数学教学越来越强调学生对于数学文化以及数学史的学习。可以这样说，数学史就是数学方法史，只有深深扎根在学生头脑中的数学思想方法随时随地地发挥作用，才能使他们终生受益。同时，学习古人先进的数学思想方法，从情感态度与价值观来看，又非常有利于培养学生的爱国心，激发学生的民族自豪感。

问题2：根据祖暅原理，如何构造模型来推导球的体积公式呢？

（由于该模型的构造具有较大的难度，因此这里采用小组讨论的方式展开教学，充分发挥集体的智慧）

设计意图：在这节课之前，学生已经学习了圆柱和圆锥的体积计算公式，因此学生能够比较容易地想到这两个几何体。并且这两个几何体的截面中均有圆的出现，因此这样提问能很快引导学生往这两个几何体去思考。

追问1：我们先推导半球的体积计算公式，并且将大圆面放在一个平面中，那么根据祖暅原理，我们选取的几何体应该满足什么条件呢？

设计意图：帮助学生再次认识利用祖暅原理推导几何体体积的根本原理，明确构造的方向和要求：将半球和几何体夹在两平行平面之间，并使得用任意平行平面去截这两个几何体，截得的截面面积相等。在这个教学环节中，采用的是学生探究为主，教师点拨启发为辅的策略，可以让学生先谈谈自己的想法，如果遇到困难，教师予以帮助。具体可以按以下几个步骤引导学生构造：

（1）假设该平面截得的球的截面为圆1O，且设OO=h1，则所以该平面截另一个几何体所得的截面面积亦为请同学们思考什么平面图形的面积是具有这样的结构？

（2）该结构的面积可认为是一个大圆的面积减去一个小圆的面积，因此可以联想到的是圆环，且该圆环的外圈半径为定植R，内圈半径为变量r。且从俯视图看，r随着h的增大而减小，当h=0时，内圈变为一个点。因此从俯视图来看，该截面为一个大圆中有一个同心的小圆随着高度的增加在不断扩大，直到和大圆重合。由此可联想到构造的几何体为一个半径和高度均为R的圆柱体中挖去一个地面半径为R，高度为R的圆锥。

设计意图：从球的截面出发，结合截面的面积形式引导学生联系之前所学习的知识展开联想，让学生经历一个如何由已知来探究未知的过程，体验通过自己分析构造模型的成就感，同时在这个过程中也让学生体会到了古人的智慧。

3.拓广思维，深入研究

事实上，除了将用祖暅原理推导球的体积公式之外，我们还有很多其他的方式进行公式的推导，例如在之前学生可能会提到地将球切成“土豆片”的方式，如图所示：

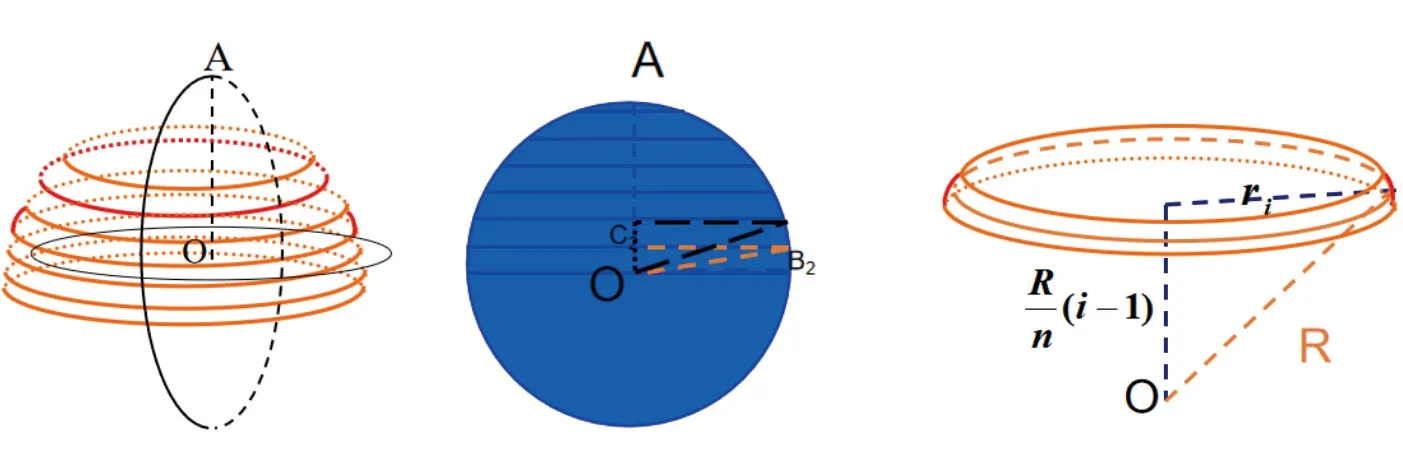
设计意图：①拓广学生的思维，再次从“分割”的角度来研究球的相关问题，进而渗透微分的思想。②球的截面问题是高考数学中经常会考查的内容，而这类问题往往放在一个由球的半径、截面半径以及球心距组成的直角三角形中解决，因此在平时教学中也可以不断向学生渗透这样的思想方法。

四、课堂小结

问题3：本节课你学到了哪些知识？有哪些收获？

（1）学习通过类比的思想研究球。

（2）在公式的推导中体会数学中一种重要的思想：极限思想。

（3）在探究过程中体会构造模型的方法，在公式推导中感悟古人的智慧。

六、教学反思

1.不论是在教材中还是在教参的教学建议中，对这节课它们采用的都是直接给出球的表面积公式和推导球的体积公式的模型，缺乏一个猜想、探究、证明的过程，对于培养程度较好的学生的思维是不利的。

2.本节课采用的是学生自主探究为主，教师点拨启发为辅的教学方式，因此在课堂中应该把更多的时间交给学生去讨论，去思考，更多地让学生上台讲解等。

3.老教材对于球的体积和表面积公式地给出比较简单，采用的是直接给出公式的方法，同时在对应公式的右侧均标注了“这个公式以后可以证明”的字样。这样的设计虽然可以节约很多时间，能让学生快速记忆并应用于计算，但不利于对于学生数学思维的培养教学。但是新教材在这两个的公式地给出上，力图向学生渗透近代数学的思想方法，同时也想兼顾学生的接受能力，对这一块内容的处理方法包含较深刻的变化思想。其中涉及了“平与曲”“近似与准确”“有限与无限”的转化，这些转化对于学生来说都是一个方法和思想上的飞跃。因此，如此教学势必会有一定的难度，对教师有较高的要求。但是只要教师设计合理，对教材和教法处理得当，注意从学生的最近发展区出发，设计各个教学环节来攻克教学难点，帮助学生克服这些困难是完全有可能的。