采用残差变化控制的自适应稀疏信道估计*
2022-09-28方海涛李明齐
方海涛,卞 鑫,李明齐
(1.中国科学院上海高等研究院,上海 201210;2.中国科学院大学,北京 100049)
0 引 言
正交频分复用技术(Orthogonal Frequency Division Multiplexing,OFDM)因为其抗频率选择性衰落能力强和抗符号间干扰(Inter Symbol Interference,ISI)能力强等特点,被广泛应用于4G通信和下一代广播通信系统中。在OFDM系统中,信号在传输过程中会受到无线信道环境的衰落和延时等制约,从而导致符号间的干扰。为了有效降低ISI,提高信号传输的准确率,需要对信道状态信息(Channel State Information,CSI)进行准确估计[1]。
Donoho[2]提出的压缩感知(Compressed Sensing,CS)理论表明,利用信号的稀疏特性,可以采用较少的观测特征向量有效地恢复出原始信号信息。同时,文献[3]表明无线信道具有稀疏性,通过将无线信道的稀疏性与压缩感知理论相结合,可以在较少导频信息条件下获得较好估计性能,提高系统的频谱利用率。
压缩感知理论主要由稀疏变换、观测矩阵和信号重构三部分构成[1]。其中信号重构作为CS理论的重要部分,解决了信号由低维特征恢复到高维的问题。目前应用较多的为基于贪婪迭代的重构算法,该类算法具有计算复杂度较低、结构简单、易于实现等优点。文献[4]提出的正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法需要信道稀疏度的先验信息,但是在实际应用中,很难获取信道的稀疏度,从而影响算法的估计性能。文献[5]提出的稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit,SAMP)算法解决了算法对于稀疏度先验依赖的问题,但是其算法性能受迭代步长的影响,且在低信噪比环境下存在算法的抗噪声能力较差的问题。
为了提高压缩感知算法在信道估计中的估计性能,增强算法的稀疏度自适应性,现阶段已有大量研究。文献[6]提出基于弱选择变步长的分段自适应匹配追踪(Weak Selection Stagewise Adaptive Matching Pursuit,WSStAMP)算法,通过幂指数来控制步长选择来控制对重构原子的选取,但存在幂指数受稀疏度个数影响较大的问题。文献[7]提出了基于奇异值分解的稀疏度自适应匹配追踪算法,通过引入奇异值分解技术提高估计性能,但仍存在抗噪性能较差的问题。
为提高算法的抗噪声能力,解决稀疏度依赖的问题,本文提出一种基于残差变化控制的正交匹配追踪(Residual Change Control Orthogonal Matching Pursuit,RC-OMP)算法。该算法通过比较每次迭代下的残差变化的幅度来控制信道估计的迭代次数,解决了传统重构算法在信道估计中存在的选径多估、漏估的问题。同时,在低信噪比环境下,利用OMP算法每次选择相关性最大的原子,控制引入不理想原子的影响,提高算的抗噪声性能。相较于传统的稀疏度自适应重构算法,所提算法具有更好的估计性能和更低的算法复杂度。
1 系统模型
1.1 压缩感知理论综述
根据CS理论可知,若信号本身具有稀疏性或具有在某个变换基下具有稀疏性,以少量的观测值能有效恢复原始信号[1]。
设信号x是N维的离散时间信号,该信号通过一个N×N变换基矩阵和一个稀疏向量相乘获得,则信号x可表示为
(1)
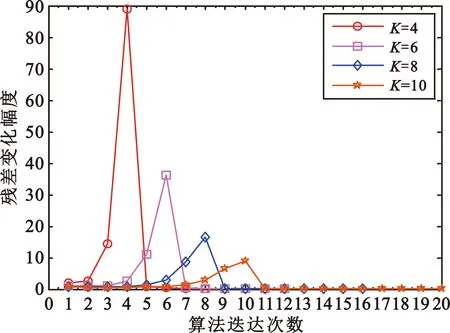
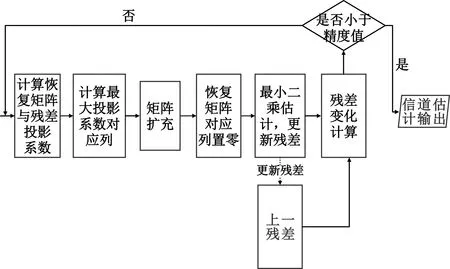
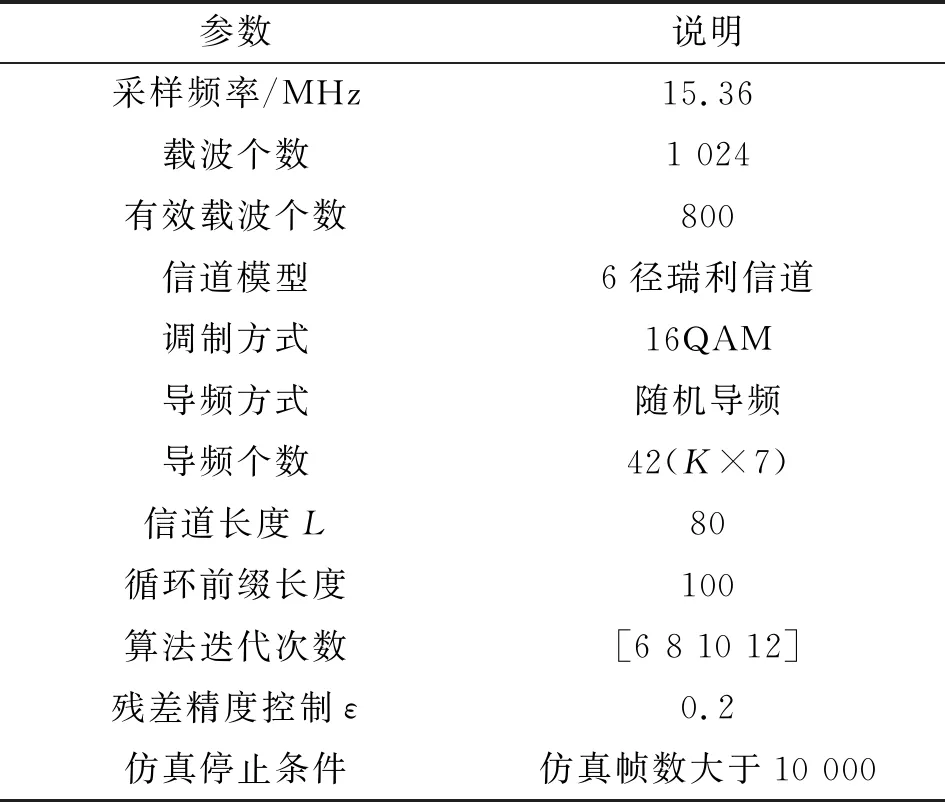
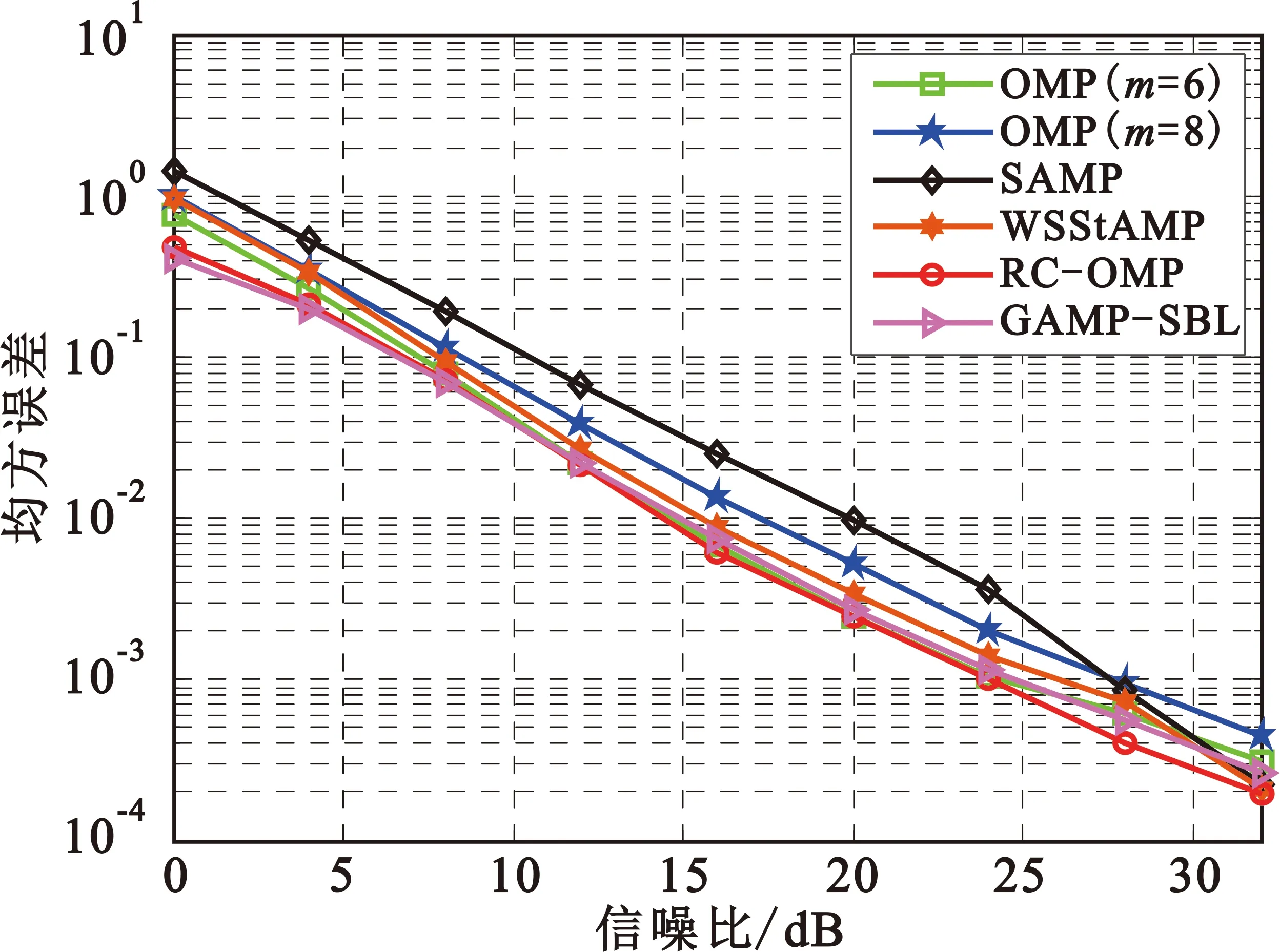
式中:s为加权系数向量,ΨN×N表示变换基矩阵。若向量s中非0个数元素为K,且满足K< 为了实现对信号的降维,即将N维信号减少到M维(M小于N),需要一个M×N的测量矩阵对原信号进行降维操作,从而获得包含信号x大部分信息的测量向量y,即 y=Φx+n=Φ·Ψs+n=Θs+n。 (2) 式中:Φ为M×N维的测量矩阵;Φ和变换基矩阵Ψ相乘得M×N维矩阵Θ,称为恢复矩阵。通常需要根据已知的测量值和恢复矩阵信息来恢复原信号,测量矩阵Φ需要满足等距约束性(Restricted Isometry Property,RIP),即需要满足 (3) 为对式(1)进行求解,现有文献中提出了多种信号重构算法[8-11]。 假设OFDM系统的子载波数目为N。在发送端,输入的比特流经过编码、调制、子载波映射和导频插入等操作后得到频域发送信号X(k),k=0,…,N-1。其中,导频个数为P,信道长度为L,则接收信号可表示为 y=XH+n=XWh+n。 (4) 式中:X为主对角线元素为X(k)(k=0,…,N-1)的对角矩阵;y=[y(0),y(1),…,y(N-1)]T为接收信号;H=[H(0),H(1),…,H(N-1)]T为信道频域响应采样;n为复加性高斯白噪声;W为N×N维傅里叶变换矩阵的前L列, (5) 接收到的导频信号为 yP=XPWPh+nP=Th+nP。 (6) 式中:XP为从N个子载波位置中选择出的P个导频位置。令S为N维单位矩阵中选择与导频位置对应的P行,则XP=SXST,WP=SW。此时,从yP、XP、WP中估计h可看作是稀疏信号的重构问题。 研究发现,在压缩感知信道估计过程中,残差的变化幅度随迭代次数变化较为明显。通过计算训练信号yP在不同稀疏度K下的OMP重构算法的前后两次残差幅度变化发现,在较高信噪比条件(24 dB)下,当迭代次数超过稀疏度K时,或估计出信道的所有延时位置时,残差的变化趋于平稳,近似为0,如图1所示。所以可利用基于残差变化的压缩感知信道估计来控制算法的迭代次数,进而减少不理想原子的引入,摆脱传统匹配追踪类算法对信号稀疏度先验条件的依赖。 图1 不同稀疏度下残差变化的幅度 虽然利用传统的压缩感知重构算法可以对OFDM系统的信道进行估计,但是在实际场景中却存在无法准确获取信道的稀疏度信息的问题。基于稀疏度自适应的信道估计方法可以实现对稀疏度的自适应估计,从而解决了稀疏度未知的问题。 文献[5]提出的SAMP算法解决了压缩感知信道估计的稀疏度依赖问题,但是算法对于迭代步长具有较高的依赖性,存在过度估计或者估计不足的问题;同时,相较于OMP算法,SAMP算法在低信噪比时受噪声影响较大,亦存在抗噪性能差和估计不准的问题。 针对SAMP存在的问题,本文提出一种基于残差变化控制的正交匹配追踪(RC-OMP)算法。算法步骤如下: 输入:输入信号yP,恢复矩阵T=XPWP,残差变换精度ε,最大迭代次数M。 Step1 更新迭代变量t=t+1,计算恢复矩阵的列向量和残差的投影系数(内积值)p=|THrt|。 Step2 选择最大投影位置pos=max{p},并将恢复矩阵对应的pos列放入增量矩阵A中A=[AT(:,pos)],并对恢复矩阵中的已投影矢量置零。 Step5 若迭代变量t小于预设迭代次数M,或者残差变化精度大于残差变化精度ε,更新残差返回Step 2;否则退出迭代。其中,残差变化ε计算等式为 (7) 式中:rt-1和rt分别表示上一次的残差与更新残差。ε主要导频受个数以及稀疏度的影响,为了更好控制残差变化精度,ε取值范围为0.01≤ε≤0.3。 传统的OMP算法主要依赖于迭代次数,当迭代次数较大时,则会引入冗余的原子;反之,则会存在估计原子不足的问题,导致估计性能变差。SAMP算法依赖于支撑集的大小,在原子预选阶段通过固定选取相关性较大的L个原子来进行重构,支撑集大小受迭代步长的控制:当步长较大时,支撑集变大,则会引入冗余原子,造成重构性能的降低;步长较小时,为达到较好性能则会导致复杂度的增加。上述算法都没有考虑在信道估计中的残差随迭代次数的变化。 本文提出的RC-OMP算法在OMP算法的基础上添加了残差变化控制逻辑,通过控制残差变化的幅度来相应调整算法的迭代次数;在低信噪比环境下,通过每次选择相关性最大的原子来降低引入不理想原子带来的不利影响。同时,残差变化幅度主要依赖于残差总功率变化的影响,在低信噪比下通过有限次选取最大相关的重构原子来降低残差能量,避免了噪声的影响。相较于SAMP算法,RC-OMP具有更好的抗噪声性能。RC-OMP算法流程如图2所示。 图2 RC-OMP信道估计流程图 本文在单天线OFDM场景下对RC-OMP算法进行性能仿真及评估,系统信道径时延随机分布,径增益为零均值复高斯随机变量,各径平均功率随时延呈负指数衰减,具体实验参数设置如表1所示。 表1 仿真参数设置 同时,为比较所提RC-OMP算法与现有基于压缩感知的信道估计算法的性能,本文利用均方误差(Mean Square Error,MSE)来作为衡量标准,计算公式如下: (8) 图3所示为所提RC-OMP算法与传统OMP算法[4]、SAMP算法[5]、WSStAMP算法[6]以及GAMP-SBL[12]算法的MSE性能对比。从图3 可以看出,在相同信噪比(Signal-to-Noise Ratio,SNR)条件下,RC-OMP算法在MSE性能上要明显优于SAMP和WSStAMP信道估计算法。通过比较不同迭代次数下的OMP算法MSE性能发现,随着迭代次数的增大,估计算法性能逐渐变差。这是由于迭代次数较大时会出现估计信道径数变多的现象,从而导致MSE性能的降低。另外,在相同的SNR条件下,RC-OMP算法相较于SAMP算法有更好的估计性能,高信噪比时SAMP算法MSE性能增强。总体上,所提RC-OMP算法相比SAMP信道估计算法约有4 dB的性能优势。 图3 不同算法的MSE性能比较 在实际系统中,OMP算法的迭代次数增加会造成信道估计的冗余问题,过多的估计会影响信道估计性能。图4给出了RC-OMP算法与OMP算法在不同迭代次数m下的MSE性能对比。从图4可以看出,OMP算法对于信号稀疏度的先验信息依赖性较强,迭代次数的增加会引入冗余径,使得算法的估计性能变差;相较于OMP算法,RC-OMP算法具有更优的MSE性能,同时也具有更好的自适应性。这是因为RC-OMP信道估计算法引入残差变化控制(式(7))的判决条件,避免引入冗余的重构原子,保证了在较大的迭代次数下能够快速收敛,从而获得较好的估计性能。 图4 不同迭代次数下的MSE性能比较 图5给出了SNR为20 dB时不同导频个数下的OMP算法、SAMP算法和RC-OMP算法的MSE性能比较。根据压缩感知理论可知,为了保证信号能够重建,测量数据数目需要满足M>4K。为比较导频数目对算法性能的影响,仿真比较了导频数目在4K~9K下的OMP算法、SAMP算法和RC-OMP算法的性能。从图5可以看出,当导频数目较小时,测量信息较少,信道估计的性能较差;当导频数目增加,测量信息量变多,信道的估计性能增强;当导频数目大于7K时,估计性能变化趋于平缓。同时,从图5可以看出,相较于OMP算法,RC-OMP算法在少量的导频条件下也具有较快的收敛性能;同时,相较于SAMP算法,RC-OMP算法抗噪声性能更优,具有更好的估计性能。 图5 不同导频个数下的MSE性能比较 由于RC-OMP算法通过设置残差变化精度来控制算法迭代,考虑到残差变化精度对算法性能的影响,图6给出了不同信噪比下残差变化精度对算法估计性能的影响。从图6可以看出,不同信噪比下性能随残差变化趋势基本一致:残差变化精度较小时,无法较好地控制算法迭代,引入冗余因子,影响算法估计性能;当残差精度较大时,算法提前停止迭代,估计信道稀疏度减少,信道估计性能变差。 图6 不同残差精度下的MSE性能比较 在计算复杂度方面,用运算时间对算法的复杂度进行近似估计。本文的仿真硬件为Intel i7-4710HQ,CPU为2.50 GHz,RAM为4.00 GB,操作系统为Microsoft Windows 10。表2是三种算法在不同信噪比条件下的运算时间比较,可以看出,所提算法在计算复杂度上均低于对比算法。 表2 不同算法在不同信噪比下的运算时间 结合图3、图4和表2可以得出,在不影响算法复杂度的前提下,所提RC-OMP算法能够提高信道估计的性能。 针对压缩感知信道估计依赖稀疏度先验以及传统自适应压缩感知信道估计算法估计性能较差的问题,本文提出了一种基于残差变化控制的OMP信道估计算法,即RC-OMP信道估计算法。仿真结果表明,相较于传统的SAMP算法,RC-OMP算法能够解决SAMP算法在低信噪比下估计性能较差的问题,同时具有更低的算法复杂度,因此具有较高的实用价值。 考虑到实际无线通信系统的应用,下一步将研究运用该算法解决实际通信系统中由均匀导频导致的压缩感知信道估计不适用的问题,进一步提高算法的应用可靠性。
1.2 OFDM稀疏信道模型
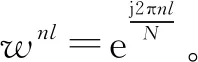
2 稀疏度自适应的压缩感知信道估计
2.1 传统的稀疏度自适应压缩感知信道估计
2.2 基于残差变化控制的压缩感知信道估计
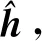
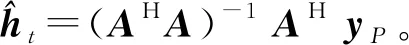
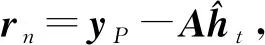
3 仿真与分析
3.1 仿真场景与参数设置
3.2 MSE性能比较
3.3 不同迭代次数下的算法性能
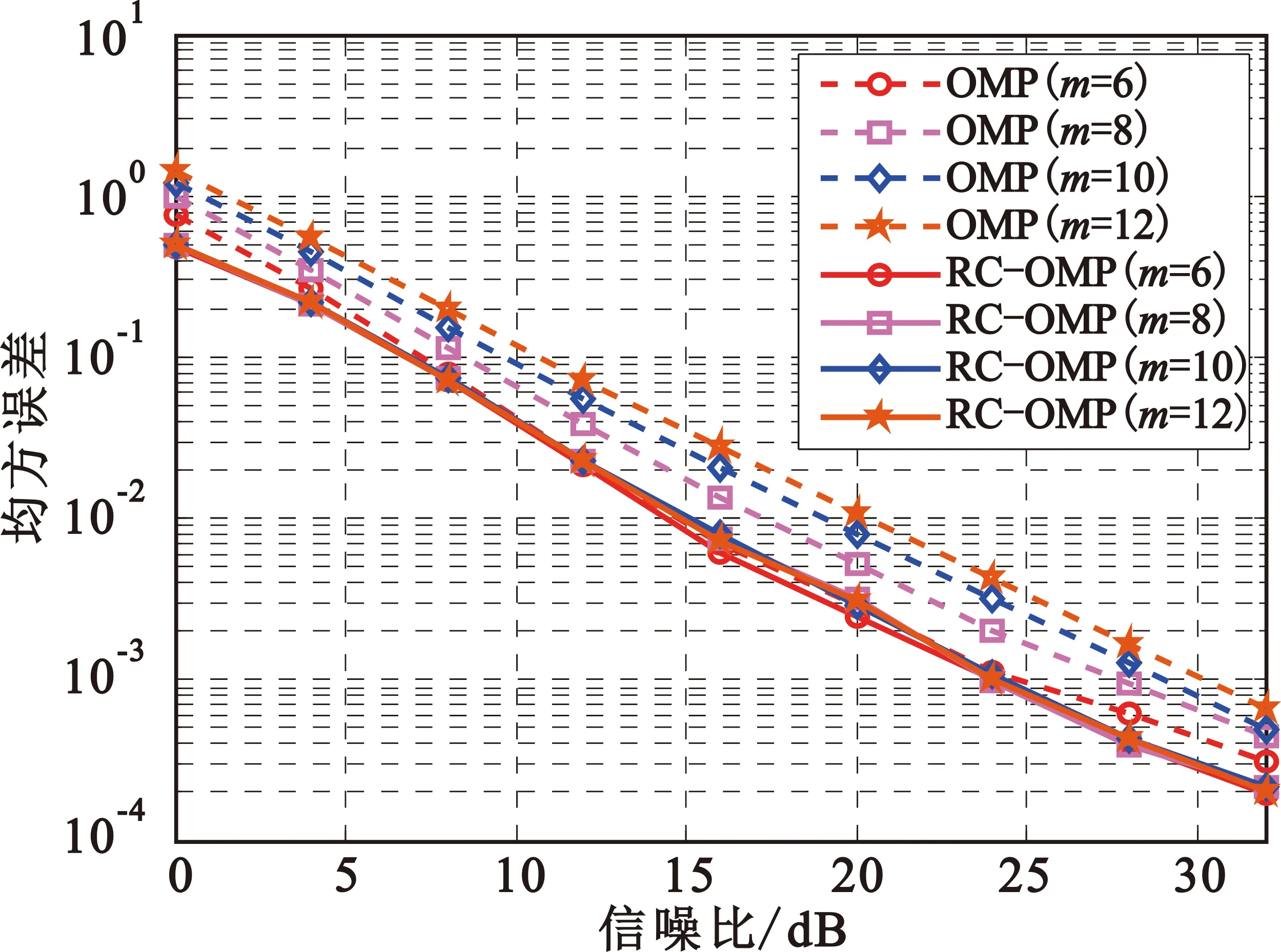
3.4 导频数目对算法性能的影响
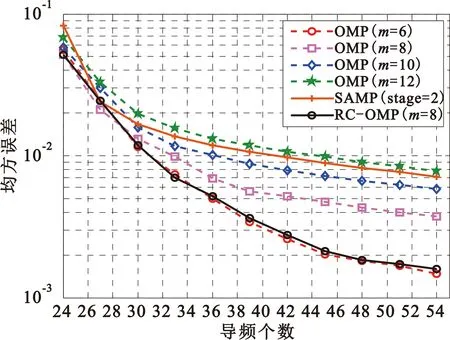
3.5 残差精度对算法的影响
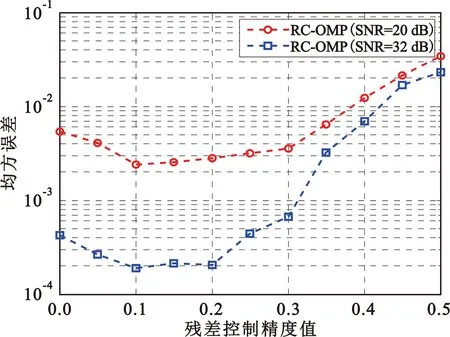
3.6 计算复杂度
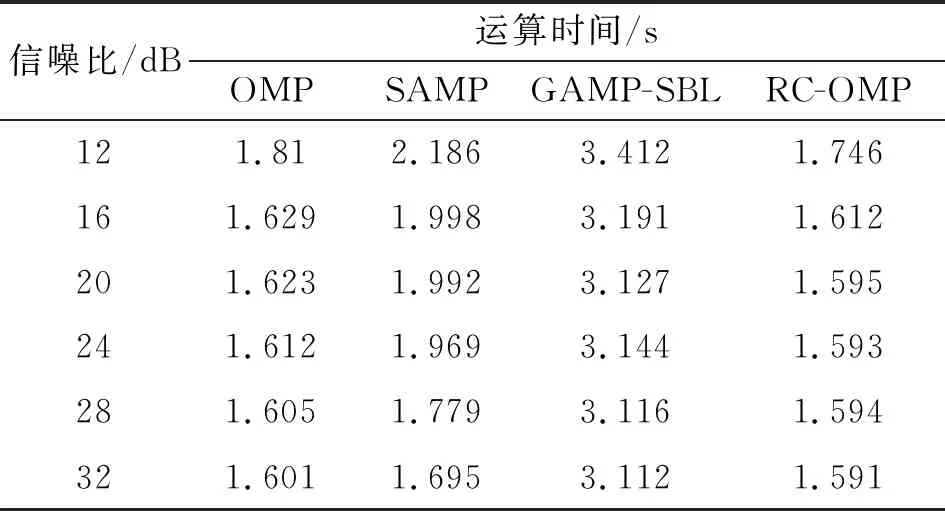
4 结束语
