多无人机协作的认知通信网络中能/谱效折中优化*
2022-09-28黄仰超谷奕龙程国兵韩蕙竹
黄仰超,谷奕龙,胡 航,程国兵,韩蕙竹,安 琪
(空军工程大学 a.信息与导航学院;b.研究生院,西安 710077)
0 引 言
无人机(Unmanned Aerial Vehicle,UAV)作为高空平台,由于其部署灵活,机动性高并通常具备较好的视距通信条件,被广泛应用于应急通信、中继通信等任务[1-2]。随着无线业务的爆炸式增长以及UAV自身能量受限等问题,实现高频谱效率(Spectrum Efficiency,SE)和能量效率(Energy Efficiency,EE)成为UAV通信技术的发展趋势。然而,提高EE可能会导致SE的降低[3]。因此,如何在UAV认知通信中进行SE-EE折中优化是一个值得研究的新问题。
在认知通信中,次级用户能够探测频谱空洞,并择机访问主用户的授权频带。文献[4]提出了地面认知无线网络中的联合感知时间和功率资源分配优化问题,但是并未考虑协作感知策略。将认知无线电技术与UAV通信网络结合是一种互利的方案[5]。
在同时考虑EE和SE提升的背景下,文献[6]仅研究了最低SE条件下EE的最大化,文献[7]仅研究了在EE约束条件下SE的最大化问题,文献[8]在求解SE和EE最大的基础上只对感知时间和决策阈值进行了联合优化,提出了地面认知通信网络的SE-EE折中优化算法。然而与地面认知通信不同的是,UAV的飞行功率和发射功率都将大程度上受到电池容量的限制,且UAV位置变化产生与次级用户之间信道和通信距离的变化也将对SE与EE产生影响,同时对于UAV认知通信网络的研究起步较晚,因此对UAV认知通信网络中的SE-EE的折中优化问题研究较少。
本文在地面认知通信网络的基础上研究了UAV认知通信网络中EE与SE折中优化问题,考虑了UAV位置变化所产生的信道增益变化以及通信功率对UAV的SE与EE的影响,从联合优化UAV认知通信的感知时间、协作感知的判决门限以及UAV的发射功率三个角度出发解决UAV认知通信网络中的SE-EE折中优化问题。
1 系统模型
假设多架UAV以小编队飞行在边界执行探测侦察等任务。如图1(a)所示,系统模型中包含1个主用户(Primary User,PU)网络和一个择机使用授权频谱的次级用户(Secondary User,SU)网络。PU网络由一个主用户发射机(Primary Transmitter,PT)和多个主用户接收机(Primary Receiver,PR)组成。PR分布在以PT为圆心、半径为rPR的圆形区域内。每个PT-PR组可以在时帧Tc内进行数据传输,多个PT-PR组以时分多址(Time Division Multiple Access,TDMA)的方式在Tc内建立链路进行通信,通信链路如图1(b)所示。

(a)无人机认知通信网络三维系统模型图

假设UAV在认知通信的过程中,UAV与SR和PT之间的通信信道为视距链路(Line of Sight,LoS),其运动所产生的多普勒效应已得到补偿,只考虑信道中的大尺度衰落,则UAV与SR和PT之间的信道增益可以表示为[9-10]
(1)
式中:f表示载波频率,c表示光速,LX为LoS条件下平均附加损耗。
1.1 频谱感知模型
无人机认知通信帧结构如图2所示。在次级网络中,M架UAV采用能量检测法进行频谱感知,在时间τs内检测PT发射信号能量并判断授权频谱是否处于空闲状态。为了节省带宽,UAV在时间τr内采用TDMA的方式将感知结果报告给FC。当M架UAV中有大于或等于K架报告授权频谱处于空闲状态时,FC判决结果为授权频谱空闲,而后UAV将数据传输给SR,通信时间为Tc-τs-Mτr。其中,K为FC的判决门限,并有1≤K≤M。

图2 无人机认知通信帧结构
在本文中,PT的忙、闲状态分别用H1和H0表示,第i架UAV的虚警概率和检测概率可表示如下[11]:
(2)
(3)

由于M架UAV的感知信道特性相同,因此它们的感知信噪比相同。通过联合式(2)和式(3),虚警概率可重新写为
(4)
M架UAV依次将感知结果报告给FC,FC经过决策融合,最终得到的虚警概率和检测概率分别为
(5)
(6)

定义PU存在的概率为P(H1),空闲的概率为P(H0),则当PU空闲时每架UAV到SR的传输速率可表示为
(7)
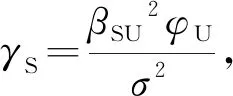
(8)
次级链路的传输将分为以下两种情形:一是FC正确检测到PU处于空闲状态,此时次级链路的吞吐量为(Tc-τs-Mτr)C0/Tc;二是FC发生漏检,PU实际处于工作状态但却被检测为空闲,此时次级链路的吞吐量为((Tc-τs-Mτr)/Tc)C1。因此,次级链路的平均SE可表示为ηSE=ηSE1+ηSE2。
ηSE1=((Tc-τs-Mτr)/Tc)CH0(1-PF)P(H0) ,
(9)
ηSE2=((Tc-τs-Mτr)/Tc)CH1(1-PD)(1-P(H0)) 。
(10)
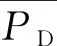
(11)
1.2 折中优化模型
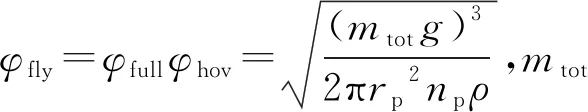

(Tc-τs-Mτr)(φfly+φhov+φU) 。
(12)
将EE定义为平均吞吐量与平均功率消耗的比值,则根据式(11)和式(12),得到UAV通信的EE为
(13)
(14a)
s.t.
0 (14b) 0<τs (14c) 0≤φU≤φmax。 (14d) 式中:φmax为UAV的最大发射功率;μ表示权重因子,且有0≤μ≤1。当μ为0和1时分别表示最大化EE和最大化SE,当μ为(0,1)中某一个具体值时该优化问题为EE和SE联合优化问题。 本文目标是通过优化UAV的τs、φU和K,解决EE和SE折中的优化问题。首先,证明存在τsopt、φUopt以及Kopt使得问题OP最优;其次,通过二分法以及穷尽搜索法分别求得τsopt、φUopt和Kopt;最后,迭代求解EE和SE折中的优化问题。 (15) 式中: (16) (17) 由此可以得出,存在最优的感知时间τsopt_SE使得ηSE最大,该最大值可以通过以下的二分法求得: Repeat IfηSE′(τs(m))<0 τs(f)←τs(m); 求出ηSE(τs(f)); end else ifηSE′(τs(m))>0 τs(0)←τs(m); 计算ηSE(τs(0)); end 计算ηSE(τs(m))和τs(m)=[τs(0)+τs(f)]/2; 计算ηSE′(τs(m)); UntilηSE′(τs(m))≤ϖ; 输出:τsopt_SE←τs(m)。 同理,求ηEE关于τs的一阶偏导数可得 (18) 式中: [P(H0)(1-PF)+(1-P(H0)(1-PD)]× (φfly+φhov+φU)- (19) G=-(Tc-τs-Mτr)M[τsφs+τrφr+(τs+τr)(φfly+φhov)]- (1-PF)[M(Tc-Mτr)(φs+φfly+φhov)+Mτr(φr+φfly+φhov)] 。 (20) 初始化: if τs(0)=τsopt_SE,τs(f)=τsopt_EE; else τs(0)=τsopt_EE,τs(f)=τsopt_SE; end (τs(0),τs(I),τs(2I),…,τs(f)); 计算δ在上述各点的值; 当τsopt_EE>τsopt_SE时,则τsopt处于[τsopt_SE,τsopt_EE] 之间;当τsopt_EE<τsopt_SE时,则τsopt处于[τsopt_EE,τsopt_SE]之间。 (21) (22) (23) 设 (24) 对其求一阶导数得 (25) 接下来分析δ与判决门限的关系。在式(5)中,对于任一个K值,PF服从二项分布。由二项分布的概率分布知识可知,随着K值的增大,PF将逐渐减小。因此,在式(11)中随着K值的增大ηSE将逐渐增大,因此,使ηSE最大的K值为Kopt_SE=M。 由式(12)和式(13)构建函数R(K,θ)=TcηSE-θE,求R(K,θ)对与K的一阶偏导数可得 (26) 令该一阶导数等于0,两边取对数,整理可得 (27) (28) 因此,存在Kopt_EE使得ηEE∈(0,θ)。结合以上分析可知,存在Kopt∈[Kopt_EE,M]使得δ最大,该最优值可通过将穷尽搜索法重置为判决门限相关参数后经过相同的步骤求得。 基于以上分析与算法,通过τs、φU与K三个参数的迭代进行联合优化使得δ值最大,该能效和谱效的折中优化算法设计如下: 初始化:精度Δ,n=1,I2,I3,发射功率最小值φmin以及最大值φmax,φU(n)=φmin,K(n)=1。 repeat 将K(n),φU(n)代入二分法和穷尽搜索法,求得τsopt; τs(n+1)←τsopt; 将K(n),τs(n+1)代入穷尽搜索法,求得φUopt; φU(n+1)←φUopt; 将τs(n+1),φU(n+1)代入穷尽搜索法,求得Kopt; K(n+1)←Kopt; δ(n)=δ(K(n),φU(n),τs(n)); n=n+1; untilδ(K(n+1),φU(n+1),τs(n+1))-δ(K(n),φU(n),τs(n))≥Δ 输出:δ(n),K(n),φU(n),τs(n)。 本节通过仿真结果来验证所提EE和SE折中优化方案的性能。PT所用频谱的中心频率为2.4 GHz,具体的系统仿真参数如表1所示。 表1 仿真参数 EE和SE随感知时间变化的曲线如图3所示,其中AND和OR融合规则下K值分别为M和1。对于三种融合规则,都存在最优的感知时间使能效和谱效获得最大值。然而,与OR和AND融合规则相比,本文所提算法提供了更高的EE和SE值。从图中可看到,AND融合规则下EE和SE的性能最差,同时,SE和EE的最大值不能同时得到,且本文所提算法下,使EE和SE最大的最优τs值分别为τs=1 ms和τs=12 ms。因此,为了联合提升SE和EE的性能,感知时间是一个需要优化的重要参数。 图3 不同融合规则下谱效与能效随感知时间变化的曲线 图4给出了感知时间和发射功率确定条件下的SE和EE与判决门限K之间的关系。由图可知,使EE和SE取得最大值的判决门限不同,且对于一个特定的γ=-5 dB时,分别在K=4和K=2时取得SE和EE的最大值。因此可以通过合理设置最优的判决门限K,使得SE和EE的折中达到更佳的性能。当感知信噪比γ发生变化时,使EE和SE取得最大值的判决门限也发生了改变。同时,当判决门限K=M时,EE和SE均处于最小值,验证了AND融合规则下EE和SE的性能最差。 图4 归一化能效与谱效随判决门限变化的曲线 图5给出了τs和K最优条件下EE和SE随μ值变化的曲线。注意到曲线不是平滑的,因为选择不同μ值时对应的最优的感知时间和K值是不同的。当μ的值从0到1变化的过程中,随着SE的上升,EE逐渐下降。μ=0对应的是最大化EE的方案设计,μ=1对应的是最大化SE的设计。同时,当考虑UAV的能量受限问题为主要因素时,可以在满足SE需求的条件下最大化EE。当考虑SU的高吞吐量时,可以在满足EE条件下的最大化SE。此时,可以根据图中所示的能谱效关系来确定适当的μ值。 图5 能效与谱效随μ变化的曲线 如图6所示,EE随着φU的增大呈现先增后减的趋势,验证了相关理论分析的正确性。随着噪声功率的增大,EE逐渐下降,且使EE取得最大值的φU值也变大。当UAV发射功率有限(如图中虚线所示为最大功率)、噪声功率为-25 dB时,φUopt_EE取在该曲线的峰值处;当噪声功率为-15 dB和-5 dB时,使得能效最大的发射功率φUopt_EE的取值均取在虚线与两条曲线的交点处,即最大发射功率为φUopt_EE。 图6 不同噪声条件下能效与发射功率间的关系曲线 图7给出了当μ=0.5时本文所提出的迭代优化算法与现有的固定发射功率方案下得到的δ随感知时间和判决门限K变化的三维曲线图,可见本文所提方案性能优于现有方案,且同时存在最优的感知时间和判决门限K使得δ最大,即该三维曲线的最高峰值,此时能效与谱效达到最佳的均衡性能。 图7 最优发射功率条件下能谱效折中参量随K与τs变化的三维图 在UAV认知通信网络中,能量效率与频谱效率的同时优化可能会发生冲突。本文研究了基于UAV协作感知的SE-EE折中优化问题,证明存在最优的感知时间、判决门限以及UAV发射功率分别使得能量效率和频谱效率最大,并通过二方法和穷尽搜索法求解最优值。然后,提出了一种联合优化感知时间、判决门限以及UAV发射功率的算法,以求解频谱效率和能量效率的折中优化问题。结果表明,本文所提方案优于现有方案,能量效率和频谱效率之间存在权衡,并且μ值不同,代表着能谱效的需求不同,μ值越小,能效性能越突出;μ值越大,谱效性能越突出。对于不同的μ值,可根据本文所提算法求得不同的一组感知时间、判决门限以及UAV发射功率值使得该能谱效折中最优。2 优化问题求解
2.1 感知时间优化

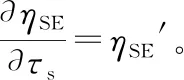
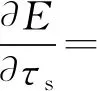
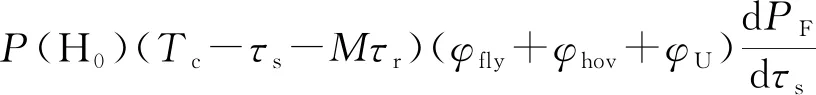


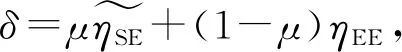
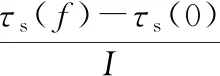
2.2 发射功率优化

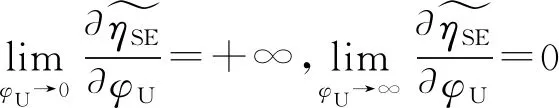



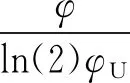


2.3 判决门限优化
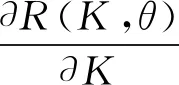


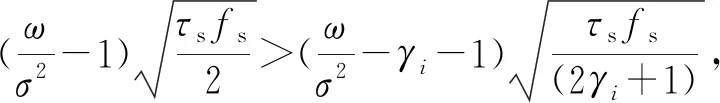
2.4 复杂度分析

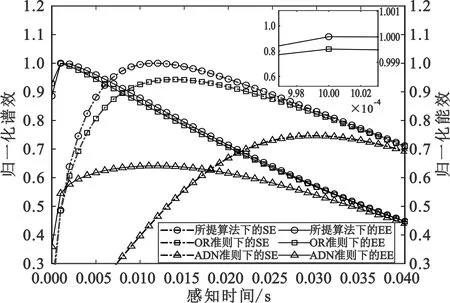
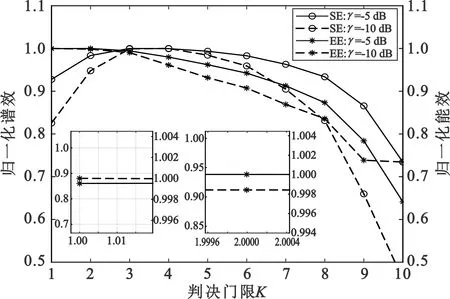
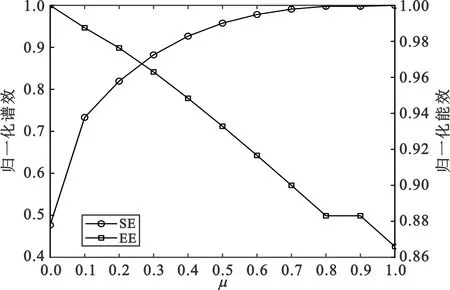
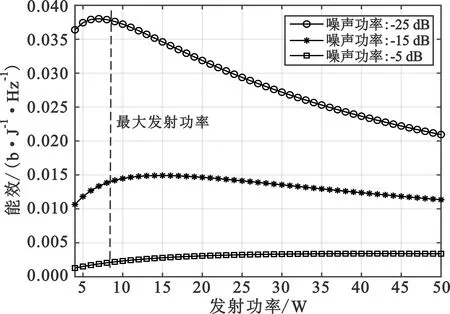
3 仿真与分析


4 结 论
