消息复用下的空间耦合LDPC码窗译码优化算法*

周 华，葛旗伟，张 锐，司 闯

(南京信息工程大学 电子与信息工程学院，南京 210044)

0 引 言

空间耦合低密度奇偶校验(Spatially Coupled Low Density Parity Check，SC-LDPC)码由Kudekar等人2011年在文献[1]中首次提出。由于SC-LDPC码的稀疏奇偶校验矩阵与卷积码半无限校验矩阵的结构相似，故其又被称为LDPC卷积码。近年来，SC-LDPC码被证明具有阈值饱和的特性，基于置信传播(Belief Propagation，BP)其译码门限(Decoding Threshold)能够达到对应规则LDPC码的最大后验概率(Maximum a Posterior，MAP)译码门限。

SC-LDPC码的研究主要包括码型的构造和译码方法。在SC-LDPC码型的构造方面，一种新的折叠型结构和一种非对称空间耦合结构分别于2017年[2]和2019年[3]提出，在很大程度上提升了SC-LDPC码在突发删除信道下的译码性能。随后，为了避免SC-LDPC码在信道中的速率损失，张亚坤等人[4]提出了一种码率无损失的空间耦合LDPC码。在译码方面，2012年，Iyengar等人[5]提出了应用于空间耦合LDPC码的窗译码方案，与传统BP译码算法相比，窗译码在降低复杂度和时延方面有一定的优势。2016年，Hassan等人[6]提出了便于硬件实现的完全并行SC-LDPC码窗译码。2018年，Klaiber等人[7]利用失速检测，提出了基于误码率预测的自适应窗口移位算法，有效地控制了窗译码突发式错误传播问题。2020年，张娅妹等人[8]提出了窗口可变的空间耦合LDPC码窗译码，通过先前窗口的对数似然比平均值计算阈值θ，若当前窗口译码产生的对数似然比值小于θ，则使窗口大小加一并重新开始迭代，这一做法有效降低了窗译码的误码率。同年，吴皓威等人[9]将分层译码引入SC-LDPC码中，使译码性能进一步改进。

虽然窗译码非常适用于SC-LDPC码，但还存在诸多局限性，如译码性能损失、复杂度和时延依然较高等。为改进这些问题，本文提出消息复用算法和动态多目标符号输出算法。仿真表明，相比于传统窗译码，消息复用算法在优化译码性能的同时，译码复杂度进一步下降；动态多目标符号输出算法与单目标符号输出的译码算法相比，误码率损失可忽略不计，复杂度明显下降，且在动态多目标符号窗译码中使用消息复用更新边信息时，译码性能明显优于传统窗译码，译码复杂度进一步下降。

1 空间耦合LDPC码

SC-LDPC码的基础校验矩阵构造基于原模图，原模图是一种二分图，与LDPC码的Tanner图结构相似，对原模图进行复制、置换交织、扩展可形成不同码长的空间耦合LDPC码[10]。原模图一般表示为(J，K)，J表示原模图中与变量节点相连的边的数量，K表示与校验节点相连的边的数量。图1(a)所示是一个(3，6)原模图单元，将该原模图复制L次，如图1(b)所示，获得长度为L的原模图序列。假设原模图序列的起始记为时刻t，则末尾时刻为t+L-1，L被称为耦合长度。

图1 原模图单元到原模图链

置换交织通过将原模图中不同时刻校验节点的边端点交换，同时保持另一侧与变量节点相连的边端点位置不变，实现不同时刻原模图的交织互连。如图1(c)所示，将t时刻的原模图校验节点的边端点分别连接到t，t+1，t+2,…,t+w时刻的校验节点，该过程又称为边扩展，其中w称作耦合宽度。当w=2时，图1(b)中每个时刻的原模图重复如图1(c)所示的边扩展，并在序列最右侧补充w个校验节点终止边扩展，形成如图1(d)所示的原模图链。

原模图的基矩阵表示方法为Bp=[bij]Jg×Kg，其中，bij表示校验节点和变量节点相连边的个数，Jg和Kg分别表示基矩阵行和列的大小。如图1(a)中(3，6)的原模图基矩阵表示为Bp=[3 3]，在边扩展的过程中，基矩阵分解为w+1个分量矩阵Bpx，x=0，1，2，…，w。图1(c)中，耦合宽度w=2，分量矩阵为Bp0=Bp1=Bp2=[1 1]，分量矩阵与基矩阵满足

(1)

将原模图链中的每一个原模图转化为矩阵形式可得到SC-LDPC码的基础校验矩阵，校验矩阵的行和列分别对应原模图链中的校验节点和信息节点。图1(d)原模图链校验节点数量为(L+w)×Jg，变量节点数量为L×Kg，对应的基矩阵形式为

(2)

为得到SC-LDPC码的稀疏奇偶校验矩阵，对BSC进行扩展，定义扩展因子M，将基矩阵中的非零元素用M×M大小的单位矩阵替换并循环移位，零元素用大小为M×M的零矩阵替换，最终得到空间耦合LDPC码的校验矩阵

HSC=[hij](L+w)×Jg×M×L×Kg×M。

(3)

以上述方式生成的SC-LDPC码的码率为

(4)

2 SC-LDPC码译码方案

2.1 传统SC-LDPC码窗译码

图2(a)展示了传统窗译码的过程，定义窗口的大小为W，w+1≤W≤L。窗口沿着校验矩阵对角带结构向右下方滑动，在窗口内执行和积算法，窗口最左边Kg×M个节点(图2(a)中右斜线部分)称为目标符号，译码结束只输出目标符号。由于原模图链中每一个原模图与向前或向后的w个原模图存在关联，故当前时刻的窗译码包含了先前窗口译码所涉及的边信息(图2(a)中左斜线部分)，这些边保存了先前窗口的输出对数似然比值，并不需要通过信道信息重新初始化。同时，边信息也将参与当前窗口的奇偶检验判断。

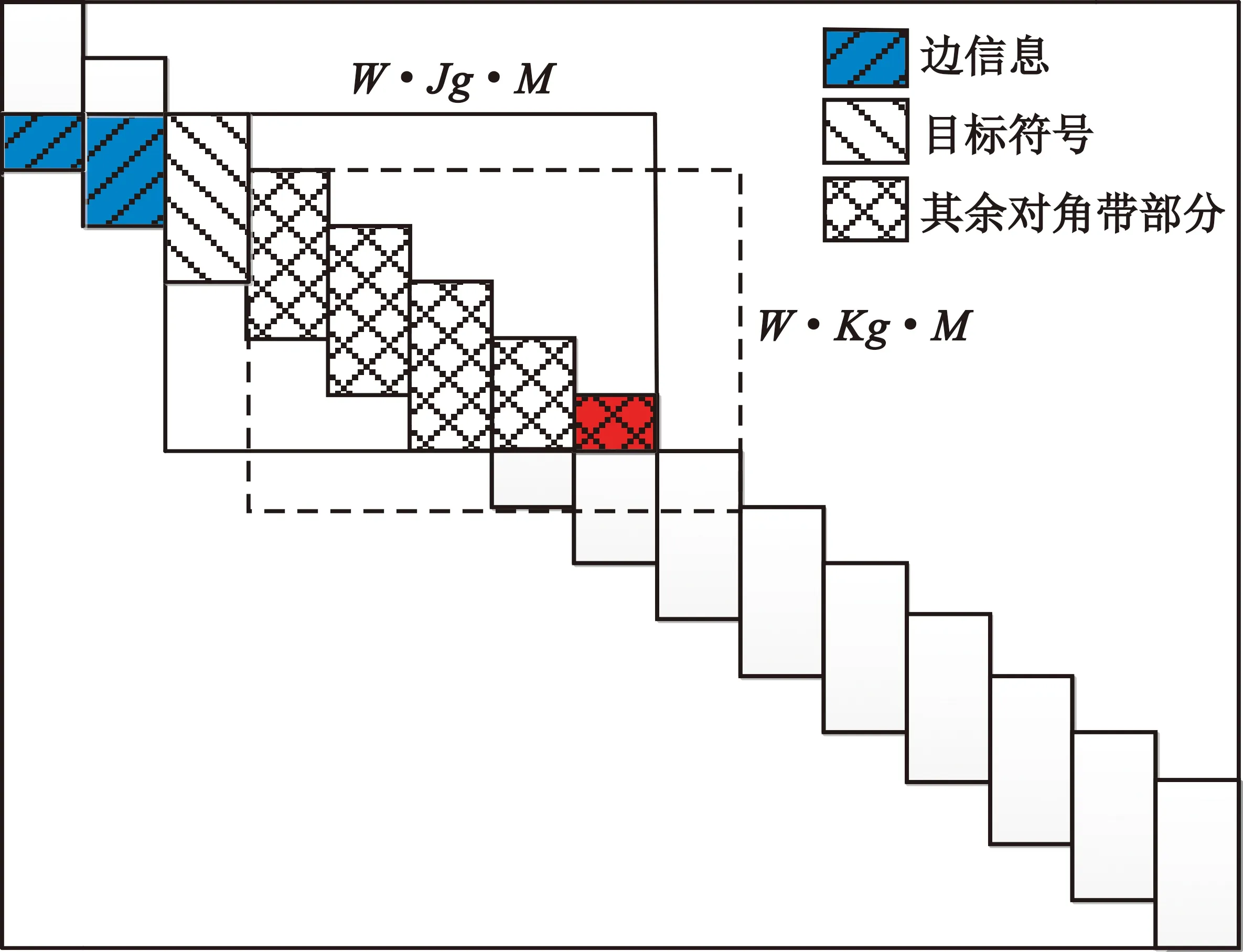
(a)传统SC-LDPC码窗译码

2.2 SC-LDPC码多目标符号窗译码

传统SC-LDPC码窗译码在每个窗口译码结束后仅输出窗口中最左边的子块(单目标符号)，导致对角带信息重复迭代次数过多，译码复杂度和时延较高。多目标符号窗译码在译码结束后输出n个目标符号，表示为n-WD，其中n为输出目标符号的数量。n-WD可有效降低传统单目标符号(1-WD)译码的复杂度及时延。

如图2(b)所示，假设窗译码输出的目标符号数量为3(图2(b)右斜线部分)，在每个窗口译码结束后，输出窗口最左边的3个目标符号，随后窗口向右滑动3Kg×M，并向下滑动3Jg×M个码元进入下一个窗口，直到整个矩阵完成译码。相比于传统SC-LDPC码窗译码，多目标符号窗译码窗口滑动次数减少，矩阵完成译码所需迭代总数降低，译码复杂度和时延均降低。但当输出目标符号数量过多时，对角带边信息迭代不充分，导致输出目标符号的误码率升高。

3 SC-LDPC码译码优化方案

3.1 消息复用下的SC-LDPC码窗译码

与全矩阵采用BP算法不同的是，传统窗译码在对目标符号译码时，产生的概率信息会以目标符号判决输出LLR(Log-likelihood Ratio)的形式传递到之后的窗口，即后续窗口的译码对先前目标符号的译码输出具有依赖性。当先前目标符号未能正确译码时，错误的输出将传递到之后的窗口并对其译码造成干扰。在多目标符号输出的SC-LDPC码窗译码中，由于迭代的不足，错误传播将更为严重。

为抑制错误传播，保持当前窗口目标符号译码的独立性，本文提出消息复用算法(Message Reuse for Window Decoding，MR-WD)，在边信息的接收方式中，以边软信息替代目标符号判决输出LLR，将存储在存储器中的外部边信息LLR以只读的形式传递到接下来的窗口。如图3(p为窗口位置)，展示了码长为768、窗口大小为6、在信噪比为3.2 dB的条件下，采用外部LLR和输出LLR传递边信息的差异。由图可知，消息复用下的窗译码目标符号的译码性能优于传统窗译码，说明使用外部LLR传递边信息的方式更加可靠。

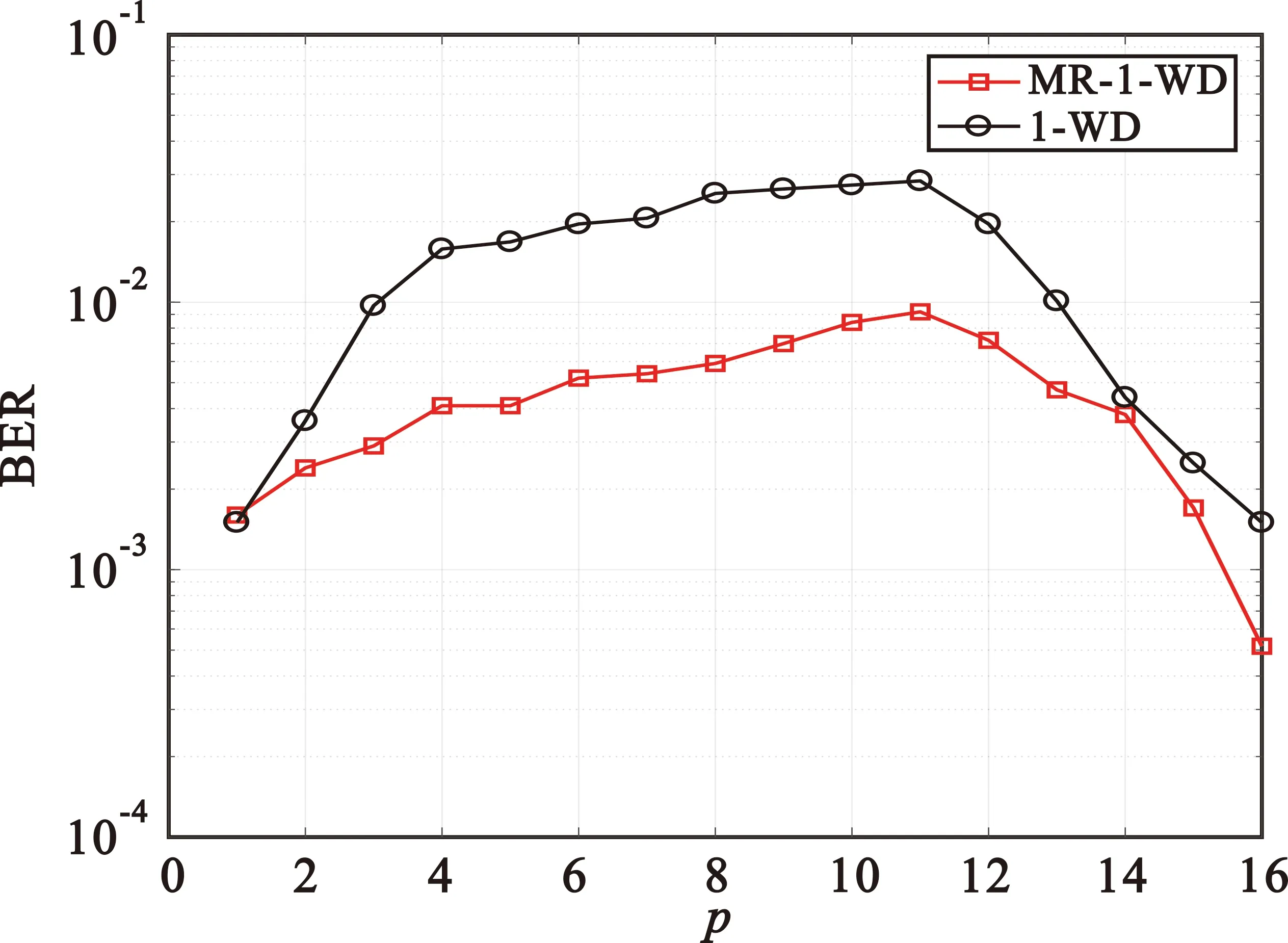
图3 两种算法不同窗口位置目标符号误码率比较

消息复用算法的伪代码如下：

输入：HSC，HWD，M，E，W，L，Jg，Kg，I，l，n

1 对初始位置的窗口初始化

forj=1:W×Kg×M

Mj→i=rj

end

2 forp=1:L/n

3 ifp>1

窗口在边信息位置(图2中蓝色左斜线)接收来自先前目标符号译码的外部LLR；对新进入窗口的信息(图2中红色网格状)进行信道信息初始化

end if

4 forl=1:I

5 对窗口中所有的i，j节点进行校验节点更新

(5)

6 对窗口中所有的i，j节点进行变量节点更新

(6)

7 判决

(7)

(8)

8 ifl=Ior [Z1,Z2,…,Zj]·HWD=0

9 break

10 end if

11 end for

12 存储外部LLR(如图2(b)绿色右斜线所示)

13 窗口向右滑动n×Kg×M，并向下滑动n×Jg×M个码元位置

14 end for

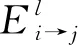
消息复用算法是一种区别于传统窗译码算法的新的边信息更新机制，其译码步骤与传统窗译码相似，主要的区别在于边信息的接收方式(算法第3步和第12步)，消息复用接收先前窗口传递的外部只读LLR作为边信息更新当前窗口的校验节点与变量节点，但这部分外部LLR并不参与当前窗口的译码迭代。在第一个窗口中，所有的变量节点均由接收到的信道信息初始化，在随后的窗口中只有最右侧新进入窗口的信息通过信道信息初始化。在奇偶校验判断阶段(算法中第8步)，HWD包括与当前窗口左边相关联的部分(如图2中蓝色左斜线部分)。

3.2 动态多目标符号输出SC-LDPC码窗译码

单个目标符号输出的译码算法优势在于译码性能的优越性，但译码复杂度仍偏高；多目标符号输出的译码算法优势在于更低的复杂度和时延，但发生突发式错误传播的可能性更高。综合两种译码算法的优缺点，本文提出一种动态多目标符号输出的SC-LDPC码窗译码(Dynamic Multi-target-symbol Output for Window Decoding，DMO-WD)，算法流程如图4所示。

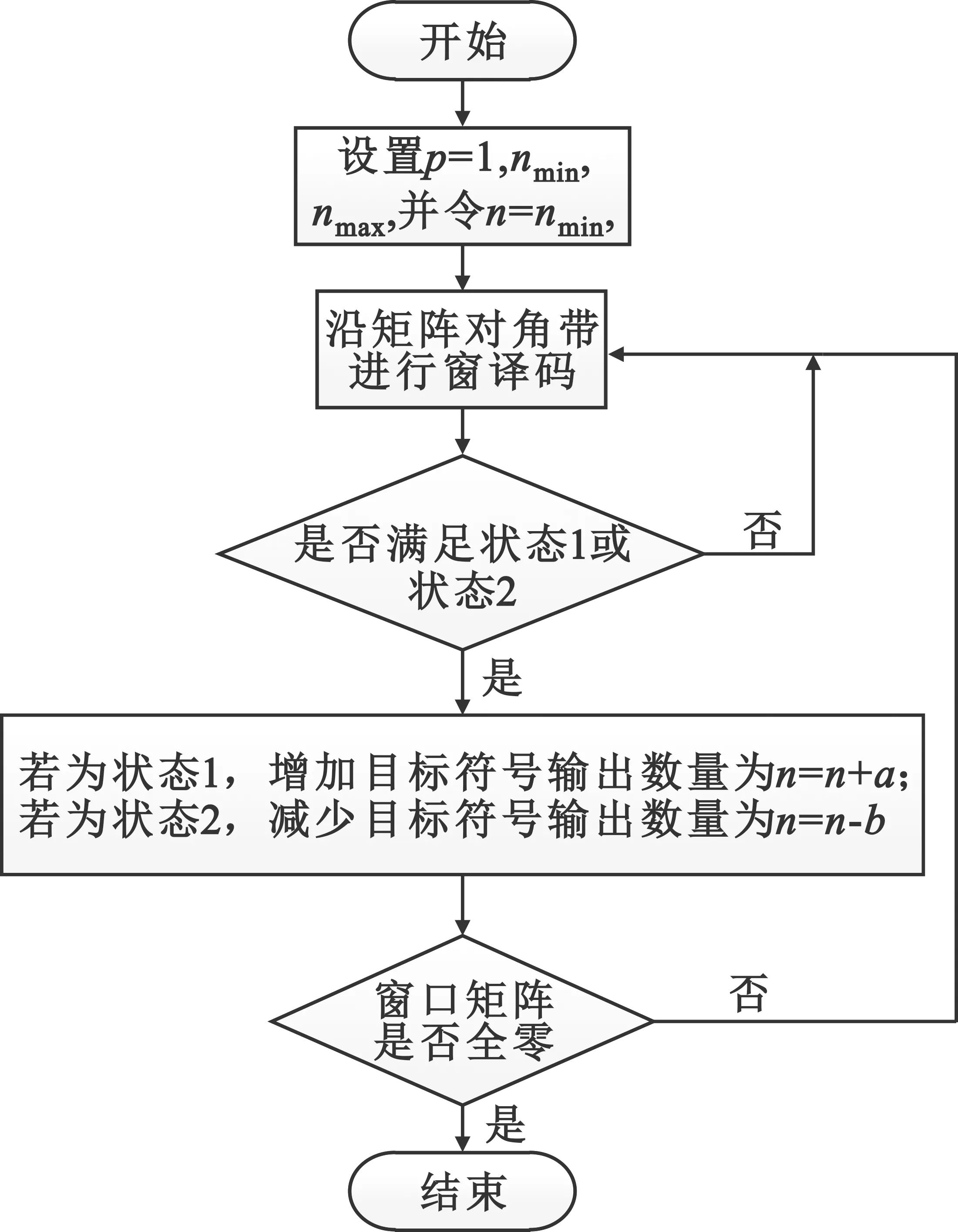
图4 动态多目标符号输出SC-LDPC码窗译码流程图

图4中状态1表示译码进程处于连续x个窗口均满足奇偶校验判定为零的状态，状态2表示译码进程处于连续x个窗口均不满足奇偶校验判定为零的状态。参考文献[7]中的分析，当译码器连续至少w个窗口发生错误输出，译码器有失控的可能，反之译码器处于稳定状态，故图4中x应满足x≥w，本文取x=w。

在译码开始时，窗口位置p位于矩阵左上角，设置输出目标符号变换的边界值nmin、nmax，并令初始n=nmin。在译码过程中，当判定有状态1或状态2出现时，增加或减少目标符号输出的数量分别为n=n+a、n=n+b直至下一个状态1或状态2出现，其中a、b为可设置的常量。在此算法中，窗口滑动的次数并非定值，故当窗口矩阵为全零矩阵时，判断窗口不再处于校验矩阵当中，跳出译码循环。

4 仿真分析

本文仿真采用码长为7 200、耦合宽度w=3、耦合长度L为60的SC-LDPC码，窗口大小设置为8，允许窗口内最大迭代次数为30次。仿真基于加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道，采用二进制相移键控(Binary Phase Shift Keying,BPSK)调制。

4.1 消息复用下的多目标符号窗译码仿真

文献[8]算法的译码原理为，设置窗口大小W的边界值为Wmin、Wmax并令初始W=Wmin，随后计算出所有窗口从初始值到最大值相应目标符号的对数似然比，累加并求平均，得到阈值θ，若当前目标符号译码产生的对数似然比值小于θ，则令该窗口大小加一并重新开始迭代。将该算法与本文提出的算法进行对比，在文献[8]中Wmin=8，Wmax=11。

图5展示了目标符号输出数量分别为1、2、4的窗译码采用消息复用带来的译码性能收益，以及和文献[8]仿真对比。由图可知，消息复用下的SC-LDPC码窗译码(MR-n-WD)性能优于传统SC-LDPC码窗译码(n-WD)性能。在误码率为10-3、输出目标符号数量为1时，消息复用下的窗译码(MR-1-WD)比传统的窗译码(1-WD)信噪比下降约0.25 dB，比文献[8]算法信噪比下降0.1 dB；输出目标符号数量为2时，消息复用下的窗译码(MR-2-WD)比传统的窗译码(2-WD)信噪比下降约0.2 dB，比输出目标符号数量为1的窗译码(1-WD)信噪比下降约0.08 dB，与文献[8]算法相比信噪比几乎无损失；输出目标符号数量为4时，消息复用下的窗译码(MR-4-WD)比传统的窗译码(4-WD)信噪比下降约0.18 dB，比输出目标符号数量为1的窗译码信噪比损失约0.05 dB，与文献[8]算法相比信噪比损失约0.18 dB。

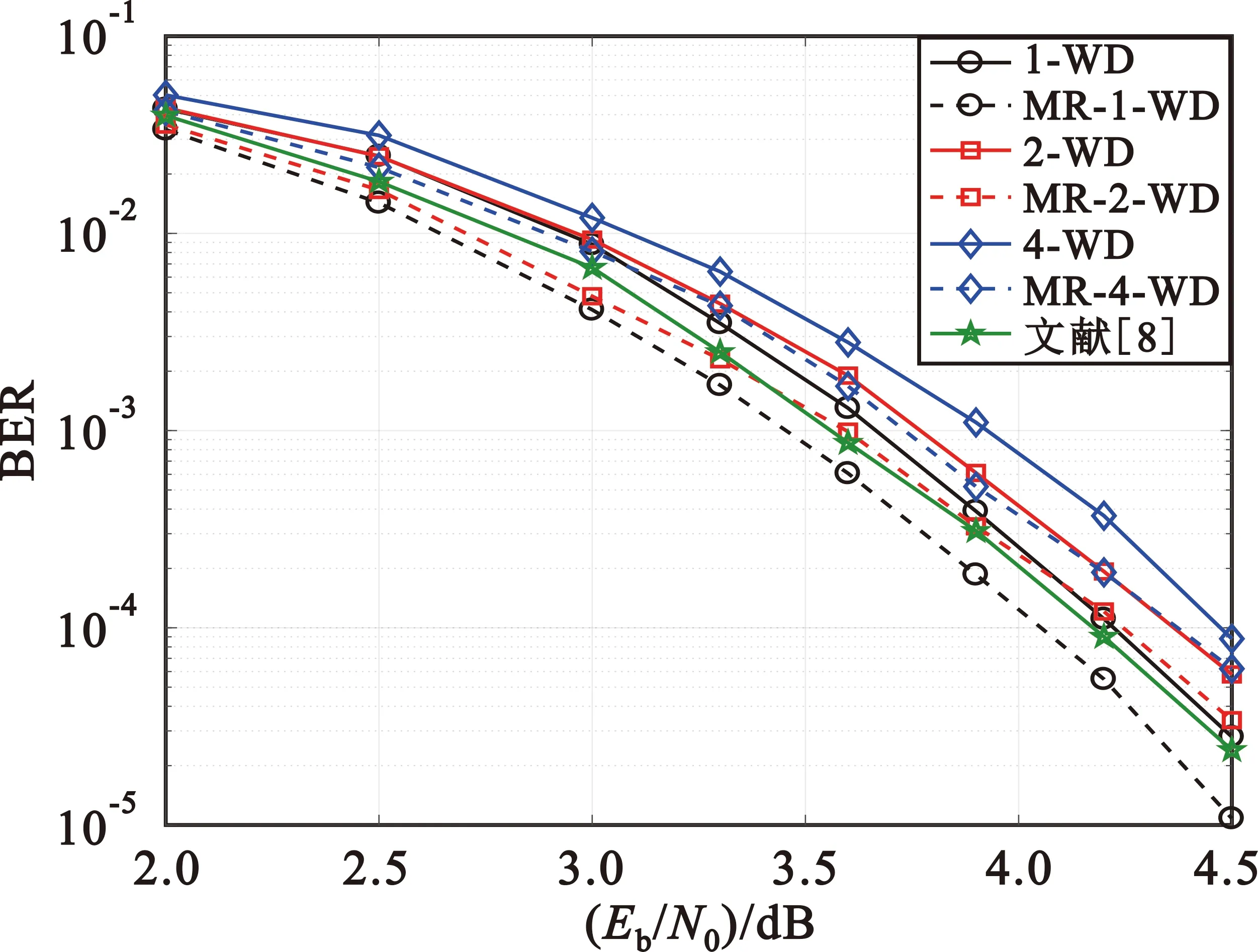
图5 消息复用下的SC-LDPC码窗译码

窗译码的复杂度与译码迭代次数紧密关联，参考文献[7]定义C为矩阵平均译码复杂度：

(9)

式中：N为窗口滑过矩阵所需要的次数，Ii为第i个窗口译码结束所需迭代次数，W为窗口大小。

图6所示为消息复用下的多目标符号窗译码与传统多目标符号窗译码复杂度对比。由于文献[8]在译码过程中增大了窗口尺寸，故其译码复杂度较高，当信噪比较低时，传统多目标符号窗译码(n-WD)与消息复用下的窗译码(MR-n-WD)窗口内迭代次数均接近设定的最大迭代次数，故差异并不明显；当信噪比升高，信道环境变好，译码所需迭代总数降低，算法复杂度越来越低，信噪比处于3～3.9 dB区间(中信噪比区域)时，消息复用算法与非消息复用算法相比复杂度差异可达到20%上下，且消息复用算法相比文献[8]复杂度下降40%以上；当信噪比大于3.9 dB时(高信噪比区域)，信道环境越来越好，两种算法复杂度差异逐渐缩小。

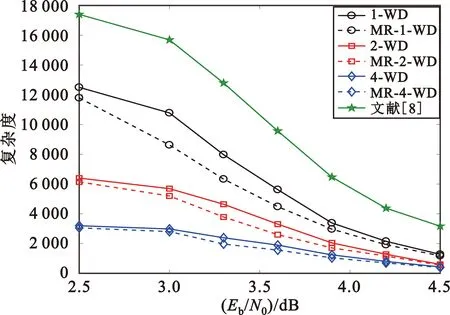
图6 消息复用下的多目标符号窗译码复杂度

4.2 动态多目标符号输出仿真

图7展示了变换输出目标符号数量n的边界值对误码率的影响，图中实线部分采用传统方式传递窗译码的边信息，虚线部分采用消息复用方式。常量a、b取值分别为a=1，b=2。在误码率为10-3量级，当设定nmin为1、nmax为4时，动态多目标符号输出窗译码(DMO-WD和DMO-MR-WD)相比于单目标符号输出窗译码(1-WD和MR-1-WD)信噪比损失可忽略不计；当nmin为1、nmax=8时，动态多目标符号输出窗译码相比单目标符号输出窗译码信噪比损失依然较小；当nmin为4、nmax=8时，两者信噪比差异明显增大。

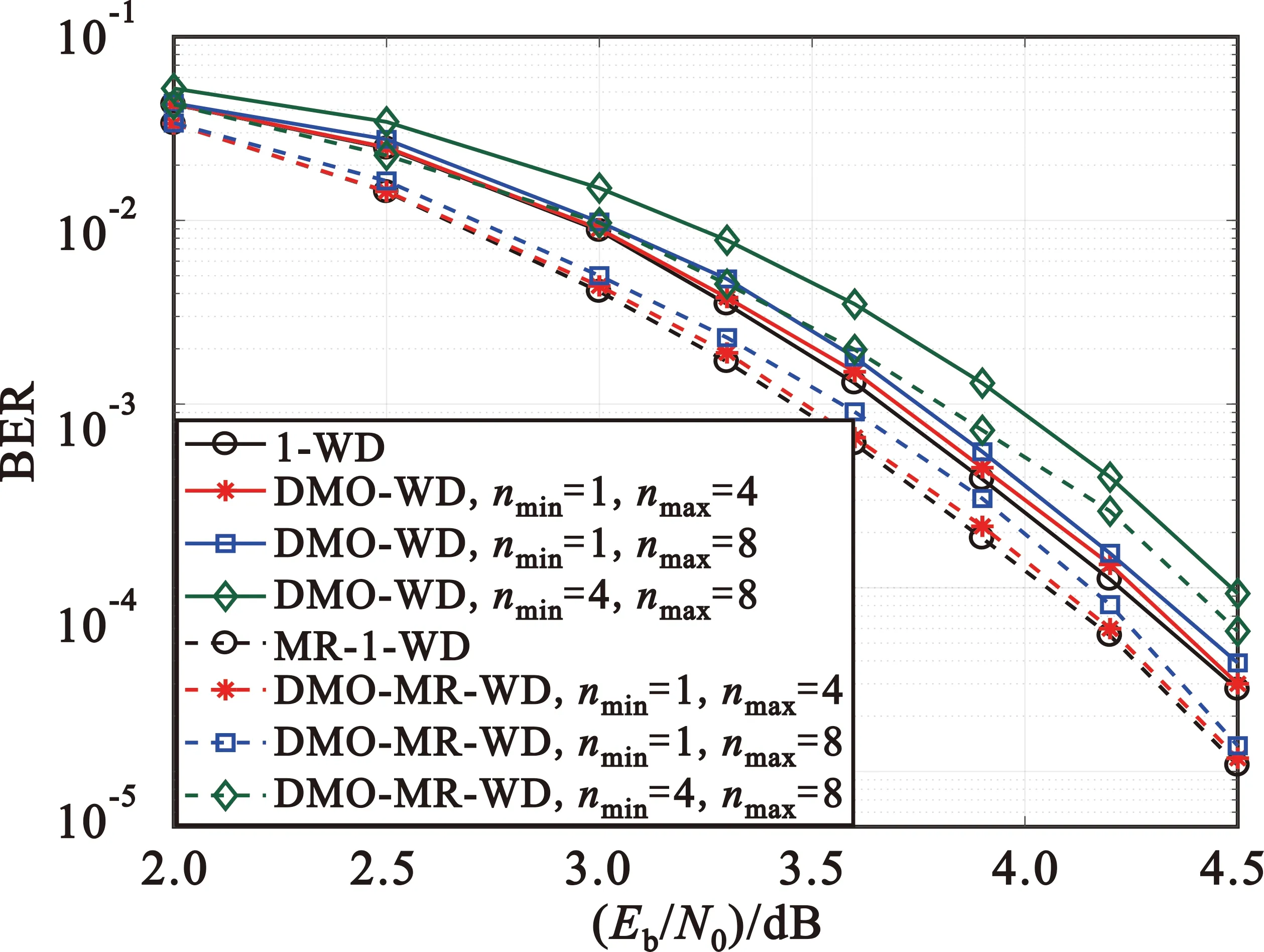
图7 不同n边界取值的动态多目标符号窗译码误码率

图8展示了目标符号增加、减少幅度值a、b的不同取值对动态多目标符号窗译码的误码率影响，设置nmin为1，nmax为4。在误码率为10-3量级，当a为1、b为2时，动态多目标符号窗译码(DMO-WD和DMO-MR-WD)相比单目标符号输出(1-WD和MR-1-WD)信噪比损失可忽略不计；当a、b值均为1时，两者差距在0.05 dB左右；当a为2、b为1时，动态多目标符号相比单目标符号输出信噪比损失0.18 dB左右。

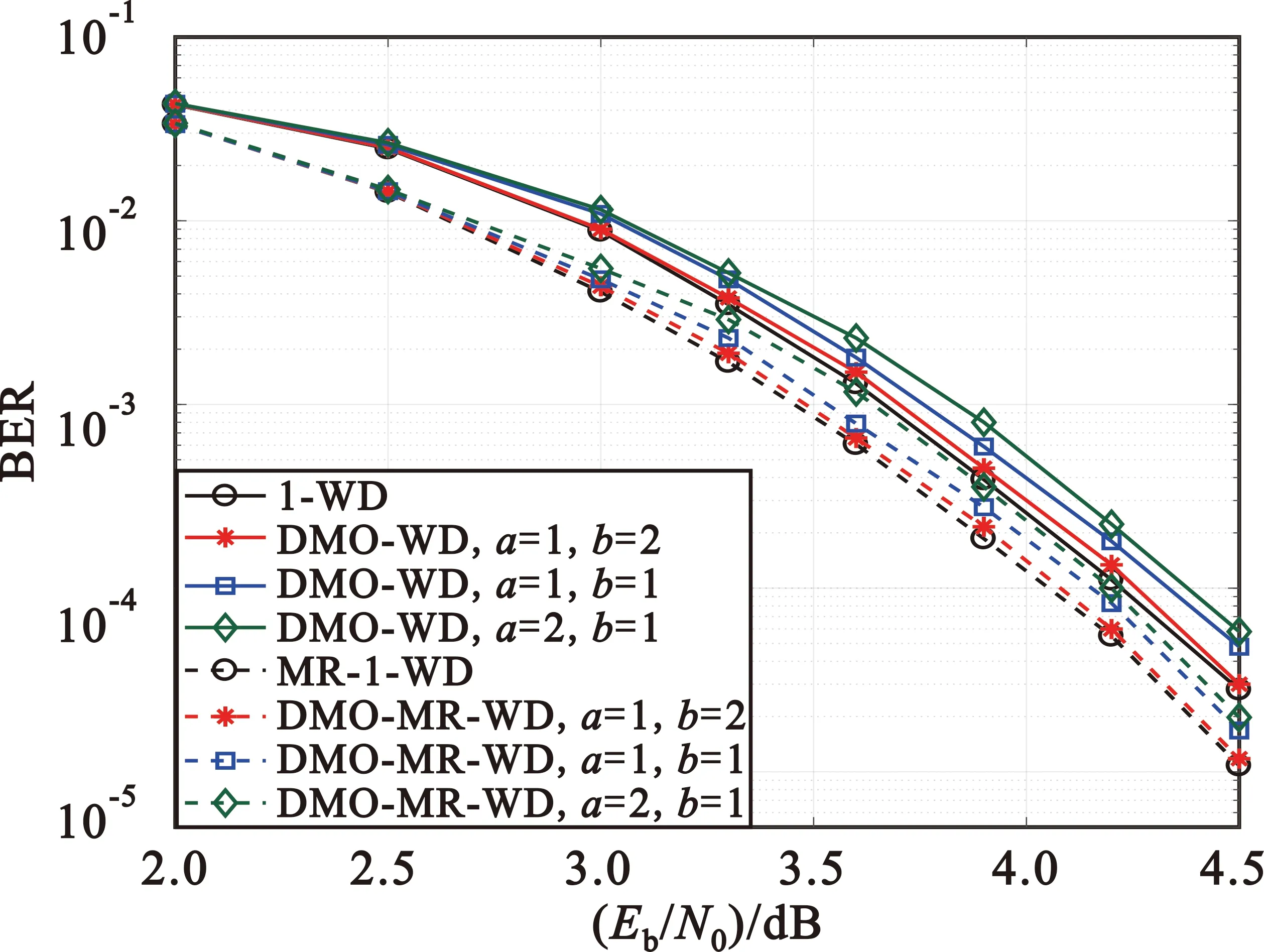
图8 不同a、b取值的动态多目标符号窗译码误码率

为比较消息复用算法、动态多目标符号算法在不同信道、调制方式下的有效性，图9展示了在AWGN信道、瑞利信道下采用BPSK、QPSK、8PSK调制方式的误码率仿真结果。在相同信噪比的情况下，高斯信道的误码率低于瑞利信道。综合图7和图8的仿真结果，在动态多目标符号输出算法中，设置nmin=1，nmax=4，a=1，b=2。综合6组仿真数据可知，误码率为10-3量级时，在同种边信息处理方式下，动态多目标符号输出算法相比于单目标符号输出算法误码率损失可忽略不计，且消息复用下的动态多目标符号窗译码(DMO-MR-WD)相比于传统窗译码(1-WD)信噪比改善0.2 dB左右，论证了该算法在其他信道或采用其他调制方式时依然有效。

图9 不同信道、调制对算法性能的影响

图10展示了几种算法在AWGN信道下采用BPSK、QPSK、8PSK的复杂度差异。在调制方式为BPSK、QPSK时，当信噪比为3～3.9 dB区间(中信噪比区域)时，在同种边信息处理方式下，动态多目标符号算法复杂度相比于单目标符号算法下降明显，如在3.6 dB，消息复用下的动态多目标符号窗译码(DMO-MR-WD)复杂度最低，相比于文献[8]复杂度降低55%，相比于传统单目标符号窗译码(1-WD)降低35%，相比于非消息复用下的动态多目标符号输出算法(DMO-WD)降低15%。而采用8PSK调制时，相同信噪比下的算法误码率较高，完成译码所需迭代总数较多，故其译码复杂度明显升高，但在信噪比为3.6 dB时，消息复用下的动态多目标符号窗译码(DMO-MR-WD)相比传统窗译码(1-WD)依然有20%左右的复杂度改善。

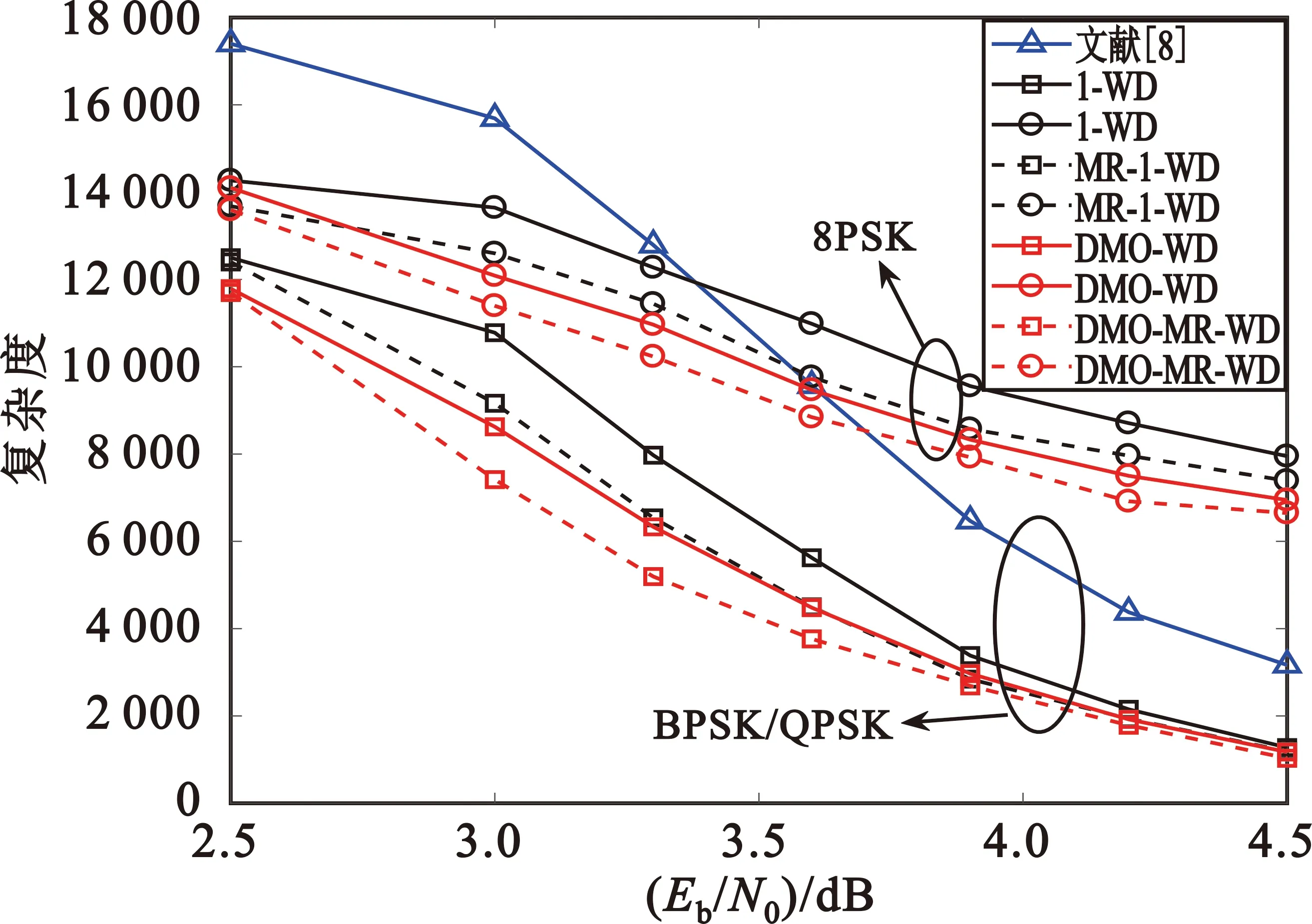
图10 动态多目标符号算法译码复杂度

5 结束语

本文针对空间耦合LDPC码窗译码提出了消息复用算法和动态多目标符号输出算法。消息复用算法以外部LLR代替输出LLR传递边信息；动态多目标符号输出算法在译码过程中借助奇偶校验来估计译码进程是否稳定，若稳定则增加其输出目标符号的数量，反之减少其输出目标符号的数量。仿真结果表明，消息复用算法较传统窗译码算法提高了译码性能，同时减少了译码复杂度；动态多目标符号输出算法与消息复用算法叠加使用时，较传统窗译码误码率下降约0.2 dB，复杂度下降最高可达35%。在该算法的基础上，未来可将消息复用低误码率及多目标符号输出低复杂度的特点应用于更多SC-LDPC码的译码算法，如SC-LDPC的窗译码分层算法。