大场景三维重建中高精度相机位姿估计

龚志杰，陈崇成

（福州大学 地理空间信息技术国家地方联合工程研究中心，福州 350108）

0 引 言

相机位姿估计问题，是指在相机内参已知的情况下，给定序列影像，求解序列影像对应的相机位置与姿态的问题。是计算机视觉中的经典问题，现已广泛应用于摄影测量、SLAM、增强现实等多个方面。

关于三维重建中的相机位姿估计，Lei等人采用网格运动统计特征匹配算法进行匹配验证。将图像序列划分为多个子序列，并分别进行独立重建与优化，解决了累积误差逐渐增大时摄像机姿态漂移验证问题。刘东生等人利用深度相机获取的深度与色彩信息，以帧到模型的方式跟踪相机，以对应点的欧氏距离和亮度信息为约束，优化全局相机位姿。但是重建时间过长，且内存消耗巨大。徐浩楠等人提出基于半直接法SLAM的稠密三维重建系统，通过半直接法优化获得较精确的相机位姿。张文哲等人提出了一种基于非共面合作目标与EPnP算法结合的单目视觉位姿测量方法。通过获得的高对比度图像和提取出的高精度中心坐标，再采用EPnP算法对动平台的位姿进行求解。但是，该方法只适用于小场景。

本文提出了一种基于增量式运动结构估计的相机位姿估计算法。该算法引入图像匹配约束条件，提高图像匹配精度，利用EPnP解决3D-2D问题，确保相机位姿估计的鲁棒性与准确性。

1 方法研究

1.1 技术路线

本文提出了一种基于增量式运动结构估计的相机位姿估计算法，技术路线如图1所示。将倾斜摄影影像和单体化精细模型白膜作为输入数据，具体步骤如下：

图1 基于增量式运动结构估计的相机位姿估计技术路线图Fig.1 The technical route of camera pose estimation based on incremental motion structure estimation

（1）利用尺度不变特征转换（Scale-InvariantFeature Transform，SIFT）算法，提取影像的特征点；使用基于KD-Tree的BBF（Best Bin First）算法，实现影像之间的特征匹配。

（2）针对特征点匹配过程中产生的错误匹配问题，采用多种约束条件，实现对匹配点对的进一步筛选。去除错误匹配的点对，并使用RANSAC算法进行几何验证。

（3）采用增量式运动结构生成方法。首先进行初始化，通过匹配点对数量与两视点间距离（基线长度），选择出一对图像作为初始图像；利用对极几何计算两者的坐标转换关系，从而建立序列重建的初始框架。初始化后主要执行步骤可做分述如下：

①选取与当前图像匹配点最多的图像（记作I）。

②对I解求PnP（Perspective-n-Point，PnP）问题来估计对应的相机位姿。

③对I进行三角测量，得到新的三维点并与已生成的三维点进行配准。

④对所有已生成的三维点和已估计出的位姿进行光束平差法处理，实现非线性优化。

迭代上述步骤，直到图像全部迭代完毕，得到所有图像的场景稀疏点云与相机位姿信息。

1.2 特征提取与匹配

1.2.1 特征提取

图像包括点、线、面等特征，本文主要讨论点特征的提取。常用的特征点提取方法有FAST算法、SIFT算法、SURF算法、ORB算法等。通过特征描述子对特征进行表示，特征描述子又被分成整体特征描述子与局部特征描述子。其中，局部特征描述子存储了特征的区域信息，被广泛应用于三维重建中。

为了确保相机姿态参数的精确度，本文选择SIFT算法进行图像特征提取，SIFT算法具有尺度不变与旋转不变性的特点，是一种稳定可行的局部特征检测与描述方法，虽然其效率不如SURF与ORB算法，但是由于SIFT算法基于浮点内核计算特征点，其提取的特征在空间与尺度上定位更为精确，有利于提高相机位姿估计的精度。SIFT算法流程步骤具体如下。

基于尺度空间的极值点搜索，检索图像所有像素点，对比像素点与其同一尺度空间及相邻尺度空间的全部相邻的点。目标图像的相邻尺度空间如图2所示。由图2可见，即需要将点所在图像的3×3邻域、与上下2个相邻的尺度空间图像的3×3邻域、共26个像素点进行比较。若点的像素值同时大于或者小于这26个像素点时，则点为极值点。

图2 目标图像的相邻尺度空间Fig.2 The adjacent scale space of the target image

针对图像尺度空间最上层与最下层缺少相邻尺度空间的情况，在顶部通过高斯模糊生成3张图，从而满足尺度变换的连续性。

由于极值点是在对连续空间采样得到离散空间的基础上进行搜索得到的，故存在一些极值点并不是真正的特征点，需要对极值点进行筛选，去除那些低对比度的极值点以及不稳定的边缘响应点，提取出正确的极值点集合。

确定特征点主方向。删除不符合的极值点后，就能够获得每个特征点的尺度，则相应的尺度空间值（，）为：

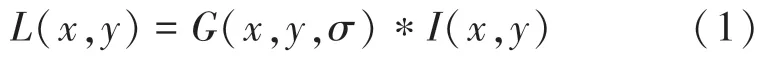
其中，

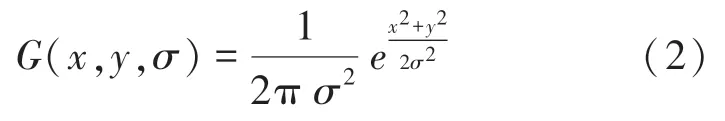
则每个点（，）的梯度模（，）可由式（3）求得，方向（，）可由式（4）求得：

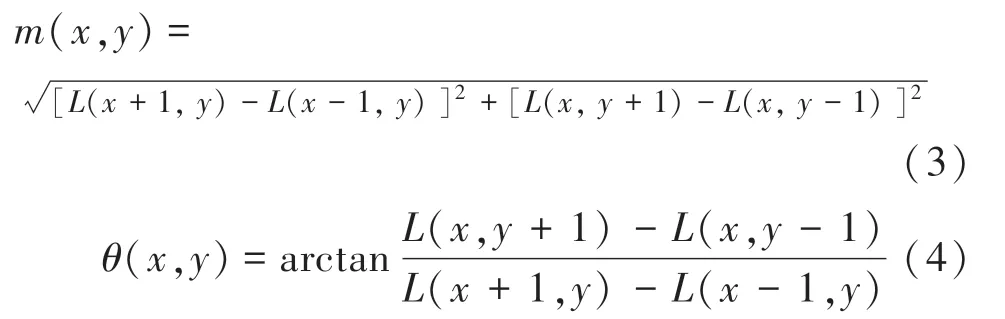
通过直方图统计梯度的幅角。直方图的纵轴为梯度幅角的累计值，横轴为梯度的方向，则特征点的主方向为直方图中最大值，辅方向为直方图的次峰值（超过最大值的80%），故特征点的方向只和像素的梯度方向有关，从而能确定特征描述子的旋转不变性特点。

生成特征描述子。经过上述步骤获得所有特征点的位置、方向与尺度信息后，通过一组向量来生成特征描述子。生成过程的步骤重点可以表述为：矫正旋转主方向，保证旋转不变形；生成特征描述子，形成一个4×4×8维的特征向量；对特征向量长度实施归一化，从而减少光照的影响。

1.2.2 特征匹配

由于是对倾斜摄影影像进行图像特征匹配，影像本身具有经纬度坐标。因此，本文借助图像的经纬度坐标设定阈值，对每张影像进行最近邻搜索，只对一定距离范围内的影像进行特征匹配，从而达到提高算法效率的目的。

通常，图像特征匹配都是利用最近邻特征点的欧氏距离同次近邻特征点的欧式距离的比值，与设定的阈值对比大小，来判断是否为匹配点对。而文献［11］中提出，匹配点最近邻特征点的欧氏距离与匹配结果的正确与否存在一定关系。当最近邻特征点的欧氏距离值超过0.3时，特征匹配正确率非常低、甚至为零。为了提高效率，本文采用基于KDTree的BBF算法，计算源图像中每个特征点到目标图像上最近邻特征点、次近邻特征点的欧氏距离。若最邻近特征点的欧氏距离大于0.3，表示匹配错误，则去除匹配点；若最邻近特征点的欧氏距离小于0.3，则继续计算最近邻特征点的欧氏距离与次近邻特征点的欧式距离的比值。以往大部分文章都是采用low推荐的阈值0.8，但由于大尺度影像中特征点较多的情况却不适用。经过多次实验比较，本文设定阈值为0.5，当最近邻特征点的欧氏距离同次近邻特征点的欧式距离的比值大于0.5时，表示源图像的特征点在目标图像里不存在匹配点，反之则表示为正确的匹配点对。

在此基础上，继续采用双向匹配的特征匹配检验方法进行验证。即：当且仅当源图像的特征点与目标图像的特征点同时匹配时，才表示此特征点对匹配正确，否则删除该特征点对。

1.3 增量式SFM

1.3.1 初始化

因为增量式SFM的重建策略是先选择种子图像进行初始重建，然后再不断地添加新的图像，所以种子图像的选择影响了相机位姿的能否恢复。同时在增量的过程中，种子模型的位置也决定着重建与相机位姿求解的准确性与鲁棒性。

初始图像对应该具有大量的匹配点对且两视点间距离（基线长度）大，能够鲁棒地估计初始2帧重构。本文选择具有最大匹配对数量的图像对，同时不能很好地构建匹配图像对之间的单应性关系。所谓单应性，就是对2张图像进行的变换建模，若单应性不能够拟合2张图像之间的对应关系，就可以推断出2张图像拍摄位置是有一定的距离，并且都涵盖了相似的三维场景结构。在估计单应性矩阵方面，本文采用RANSAC算法，根据求解过程中获得的与单应性有关的特征匹配百分比，来确定初始图像对。特征匹配的内点百分比越低，则图像侯选排名越高。同时设定一定的阈值，防止发生距离过远导致重建失败的现象。

确定初始图像对后，利用分解本质矩阵来获得初始图像的相机外参数（相对旋转矩阵与相对平移矩量）。根据对极几何的理论基础可知，本质矩阵拥有5个自由度，故其最小的支撑点为5对匹配点，即至少需要5对匹配点才能够求解出本质矩阵。因此，本文采用经典的五点法对本质矩阵进行解算。利用奇异值分解，根据本质矩阵的秩为2的属性，求解出相机的相对平移量，再构建方程组解求相机的相对旋转矩阵，得到如图3所示的4组结果。利用相机与三维点位置（即三维点必须在相机的前部）这一约束关系，来确定正确的相对旋转矩阵与相对平移量。针对求解出的本质矩阵可能不唯一的情况，本文采用Sampson距离最小约束方法，对正确的本质矩阵进行认定。

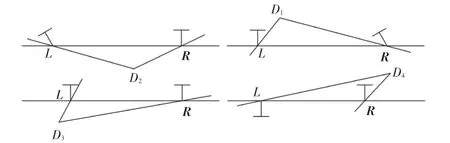
图3 本质矩阵分解获得的4组可能的解Fig.3 Four groups of possible solutions obtained by essential matrix factorization

将第一张图像的相机坐标系作为世界坐标系，即可求解出第二张图像的相机位姿。得到2张影像对应相机的相对位姿后，利用相对位姿以及2张影像的匹配点信息，采用三角测量（Triangulation）得到初始的一组三维点。

1.3.2 图像配准与点云配准

图像配准就是在初始化后，获得初始相对三维坐标与对应摄像机的相对位姿关系的基础上，不断配准新图像，并优化当前框架的过程。

新输入的影像选择十分重要，因其会对位姿的估计与三角测量的精度产生影响。本文通过从候选图像中看到的当前已生成场景三维点的数量，以及在图像中的分布情况，来选择新输入的影像。网格化每张侯选影像，用“空”与“满”来表示每个格子。若影像中某一格子可见，则将该格子表示为“满”，且该图像点评分按照权重（当前层格子的尺寸）进行调整，如图4所示。

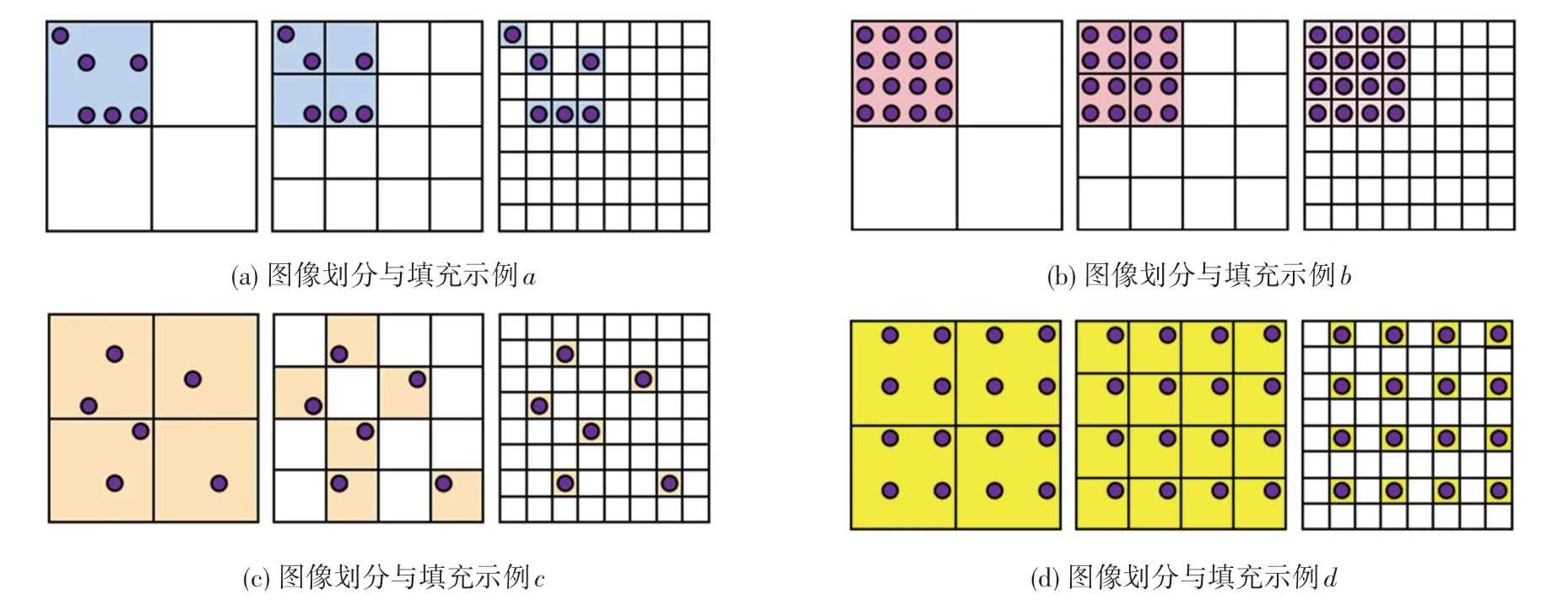
图4 图像的划分与填充Fig.4 Images division and padding

图4中，4个图像评分计算依次为：

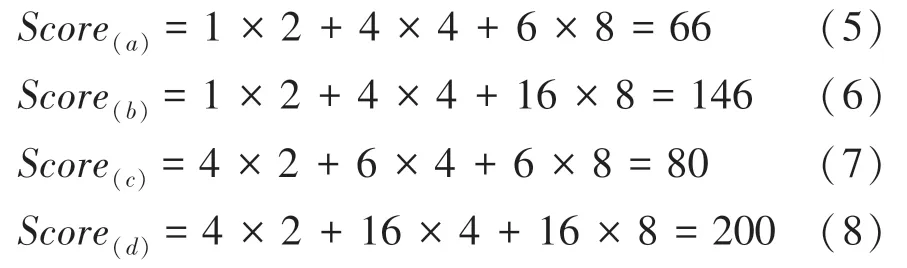
在新图像与已配准图像的匹配点中，一定存在一部分的匹配点是已配准图像之间的匹配点，即已经获得了这些特征点的三维坐标，同时又知道这些特征点的像素坐标，从而转化3D-2D相机位姿估计的问题，即PnP问题。PnP问题的目的，是根据相机的内在参数以及3D点与其2D投影之间的一组个对应关系，来确定相机的位置和方向。目前求解PnP问题的主要方法有P3P、直接线性变换（DLT）、EPnP和非线性优化方法等。以往大部分研究均采用P3P来求解PnP问题，但P3P方法对于相机远离3D平面（low parallax）或者视角垂直于3D平面的情况下效果欠佳，且无法充分利用所有的侯选3D-2D点对信息。经分析对比各种PnP求解方法，本文选择EPnP方法解决PnP问题。该方法无须迭代求解，时间复杂度为()。计算得到新输入影像的相机位姿参数后，利用三角测量生成更多的三维点后，再采用迭代最近点法（Iterative Closest Point，ICP），将新生成的点配准至原有的稀疏点云框架中。

1.3.3 光束法平差

图像配准与多视图三角化虽然具有高度相关的结果，但却是相对独立的2个步骤，相机位姿估计的不准确会影响三角测量的点的生成，同时，额外的三角测量可能会增加冗余度，产生重投影误差，从而影响相机位姿的估计，若不对这一情况进行修正改进，SFM时常会快速地漂移到无法恢复的状态，故需要通过光束平差法来优化场景结构，光束平差法是通过校正相机位姿与场景点的位置从而把重投影误差控制到尽可能小。

本文采用分阶段优化与全局优化的方式，每当重建到一定量级的时候，进行一次光束平差法优化，从而减少误差累积，并在所有影像添加完毕后，对生成的场景点云以及相机姿态参数进行全局光束平差法优化。在得到所有倾斜摄影影像对应相机的位姿参数后，利用有效方法对单体化精细模型与增量重建的点云进行几何配准，间接建立倾斜摄影影像与单体化精细模型的对应关系。

2 实验结果与分析

为了验证本文算法求解出的相机位姿信息精确度，本文采用南溪书院的倾斜影像数据进行验证。实验中的硬件环境为：VS2019、系统Windows 10、CPU R7-4800H、内存16 GB。

2.1 特征匹配精度验证

南溪书院倾斜影像序列如图5所示。由图5可知，该影像序列拥有丰富的结构与纹理信息，影像大小为6 000像素*4 000像素。

图5 南溪书院倾斜影像序列Fig.5 Oblique images sequence of Nanxi Academy

图6为采用本文特征匹配方法运行得到的前后效果对比。

图6 南溪书院倾斜影像序列匹配结果Fig.6 The matching results of oblique images sequence of Nanxi Academy

实验中利用本文给出的双向匹配作为衡量匹配精度的指标，采用本文特征匹配方法前后比较结果见表1。

表1 南溪书院倾斜影像序列匹配结果比较Tab.1 Comparison of matching results of oblique images sequences in Nanxi Academy

由此可见，本文的特征匹配算法在计算效率和匹配精度上均有一定提高，并且匹配点数也能满足增量式SFM的要求，且得到的较高精度匹配点的数量相对更多。

2.2 相机位姿参数精度验证

利用本文方法求解出倾斜摄影影像对应相机的位姿参数后，利用针孔相机成像模型，选择影像中一些突出部分、如建筑角点等，与开源框架COLMAP、OpenSFM所得到的相机位姿参数进行对比。通过三维点计算对应的二维影像坐标，统计产生的像素偏差，见表2。

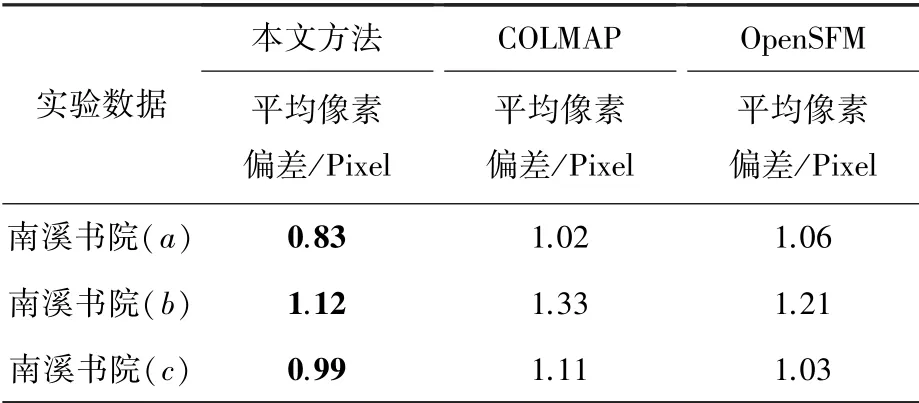
表2 不同方法求解相机位姿参数精度对比Tab.2 Accuracy comparison of camera pose parameters by different methods

由表2可以看出，利用本文方法求解出的相机位姿参数相较于COLMAP、OpenSFM在精度上有一定的提升，平均像素偏差小于1个像素点。

3 结束语

本文提出了一种大场景三维重建中的高精度相机位姿估计的解决方案，针对图像特征提取与匹配精度问题，采用多种约束条件提高特征匹配精度、去除错误特征匹配，间接提高了相机位姿估计的精度。研究采用增量式运动结构生成估算相机位姿信息，将3D-2D匹配问题转化为PnP问题，并采用EPnP方法解算相对相机位姿。实验结果表明，本文方法得到的相机位姿参数精度较高，具有较好的鲁棒性和稳定性。