基于改进模糊FP-Growth的异常检测算法

杜嘉伟，余 粟

（上海工程技术大学 机械与汽车工程学院，上海 201620）

0 引 言

随着大数据时代的来临，数据挖掘对于研究事务之间的关联规律模式有着重要的意义。目前，异常检测被广泛应用于工业控制系统、网络入侵检测、医疗异常检测等领域。异常检测是基于当前数据模式检测出其中的异常点，即检测出不符合预期模式的数据。相比较于正常数据簇，异常值数据有着与数据集中正常数据并不相同的数据特征的数据模式。

近年来，国内外学者对于异常检测的研究已取得显著成果。其算法主要可以分类4类：基于模式预测的算法模型、基于机器学习的算法模型、基于统计的算法模型、基于贝叶斯网络的算法模型。

文献［6］提出一种基于模糊孤立森林算法的多维数据异常值检测算法。该算法通过挑选一些有价值的属性建立异常检测模型，再通过隶属度判断得到评价结果，但选取的属性只能为类别型特征。文献［7］基于模糊理论，提出一种挖掘连续型数值数据的关联规则，但该算法基于正常模式的数据，无法处理黑盒数据。由此可见，上述方法大多都基于正常模式下的数据挖掘，在建立模型时要求其数据全为正常模式数据，并且要包含绝大多数的正常模式行为。在异常检测中，将没有标签标识的元数据称为黑箱状态的数据。在面对数据黑箱场景下，降低算法的误报率和漏检率，以及提高算法模型的泛化能力就成为了当下研究的热点与难点。

综上所述，本文提出一种基于改进FP-Growth算法的异常检测算法-RFPG算法（Random Frequency Pattern Growth）。对于传统数据挖掘方法中以阈值对数值型特征数据进行划分遇到的尖锐边界问题，本文提出一种基于模糊集理论的异常检测方法；对于数据黑箱问题，算法中基于baggging思想对数据随机采样，生成FP-Tree集合，挖掘出模式长频繁项集合，并通过将长频繁项集合作为输入生成新FP-Tree，挖掘模式强关联规则集，使算法对于黑箱数据有着更好的寻优与泛化能力。

1 基本概念

1.1 模糊集和隶属度

模糊集是用来描述具有模糊语义集合概念。如果存在论域，而且其中任何一个元素与（）∈［0，1］存在对应关系，则称为上的模糊集，（）称为对的隶属度。

1.2 频繁项集

采用向量和矩阵的概念，建立频繁项集（Frequent itemsets）的 挖 掘 模 型。令｛，，，item｝为个 数 据 项 的 集 合。其 中，item（1≤≤）称为项｛，，，t｝，是个事务组成的数据集，t（1≤≤）表示一条事务，且t是的子集。

项的集合称为项集（），包含个项的项集称为项集。当一个项集计算所得的支持度满足设定的支持度阈值时，则定义该项集为频繁项集。

支持度（）描述了多个项集在所有事务中同时出现的概率。事务数据集中的支持度用（）表示，支持度阈值用_表示。在挖掘频繁项集的过程中，_能够筛选并枚举出所有重要的项集。基于以上描述可推得如下定义：

给定_，若（）_，则项目集是频繁项目集。

存在项目集、，而且⊆，则（）≥（）。

1.3 FP-Growth算法

FP-Growth算法是一种频繁项集挖掘算法，该算法中使用一种FP树的数据结构作为存储结构。在面对大量输入的情况下，树存储结构可以应对复杂的数据存储问题。算法通过以频繁一项集的支持度，倒序读取事务，并将其映射到FP树中。考虑到选用的存储结构，当大量读取相同事务的情况下，已构造的重叠路径能大大减少存储时间，并减少了空间上的开销。

FP-Tree的存储结构避免了如Apriori算法那样频繁扫描数据库的I／O瓶颈，减少了I／O损耗，有着更优的时间与空间复杂度。FP-Growth算法的主要任务是找出数据集中的频繁项集，算法的主要实现步骤可依次表述为：数据采样；构建FP-Tree；基于FP-Tree挖掘长频繁项集；生成模式关联规则集；模式匹配。FP-Growth算法伪代码详述如下。

网路流量数据集，_

输出异常检测分类结果

／／对流量特征进行标准化

1：D＝（）

／／对数值特征进行模糊化处理

2：_（__（））

3：while_

／／为采样百分比

4：__（，_）

／／构建

5：__（_）

／／生成长频繁项集

6：_（_）

7：End while

／／生成关联规则集

8：____（）

／／计算数据与关联规则集相似度

9：__（，__）

／／相似度匹配

10：_（_）

11：return

2 RFPG算法

在传统FP-growth基础上，基于模糊理论的RFPG算法根据频繁项集的隶属度，以降序方式生成条件模式基。每个条件模式基在经过剪枝后，获得候选1项集，满足支持度要求的候选1项集即为频繁项集。于是提出如下定义：

若条件模式基中存在个满足_的元素，则该条件模式集基中存在最长候选1项集。

2.1 数据模糊化处理

基于模糊数学理论的综合评价方法，针对连续型数据特征进行数据模糊化处理。具体来说，模糊综合评判就是将数据模糊关系与模糊数学相关联，将难以确定边界的特征因素以隶属度的形式进行描述。

在挖掘包含大量连续数值型特征数据的关联规则时，由于传统FP-Growth算法只能处理二值化特征，无法处理连续数值型特征，因此引入数据模糊化处理改进FP-Growth算法，使算法的泛化能力更好，并能避免传统基于阈值划分时数据分类带来的尖锐边界问题。本文使用Fuzzy-C-Means算法对连续数值型数据进行模糊聚类，使用隶属度描述聚类程度。目标函数定义为：

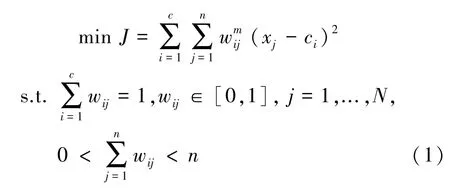
通过公式（2）计算得到聚类中心点和目标函数值，并由公式（3）重新计算权重矩阵，当目标函数值小于误差阈值结束迭代。这里用到的公式为：

将元数据集转化为模糊数据集，见表1。表1中，d表示FCM聚类后结果。

表1 模糊数据集DTab.1 Fuzzy dataset D

模糊集的隶属度使用模糊集各属性的支持度计数所得，对此可表示为：

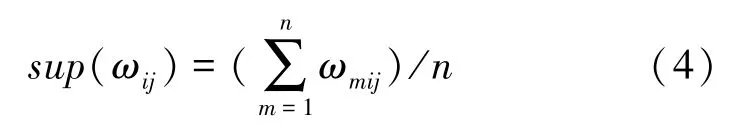
计算得出各个项集的支持度后，对候选项集进行剪枝操作，得到频繁项集。其中，剪枝包含2个步骤，可做阐释分述如下：

（1）删除不满足_阈值的候选项，得到频繁项集。

（2）删除包含非频繁（1）项集的候选项集，得到频繁项集。

2.2 异常检测

在进行异常检测之前，通常先挖掘出数据正常模式下的关联规则，但处于数据黑盒状态下的数据由于异常数据扰动，会使挖掘出的关联规则支持度与置信度会降低。因此，使用RFPG算法挖掘生成FP-Tree时，可以设置稍低的最小支持度与最小置信度阈值，以获得尽可能多的关联规则集；将各个FP-Tree集合挖掘出的关联规则集作为第二层输入，生成新的FP-Tree，由此得到接近正常模式的关联规则集。

在数据中，由于异常数据簇与正常数据簇分布不同，RFPG算法使用背离度这一概念来描述异常状态。通过规则集与单时间段数据的相似度，量化当前数据集与数据正常模式的背离度，以此建立异常检测系统的检测机制。算法中将模糊化处理后的单时间段数据与挖掘出的正常模式关联规则的交集作为单条数据的长频繁项集。对于关联规则相似度的计算，设存在关联规则与某一时间段数据，这里的支持度为，置信度为，则其关联规则的相似度可由式（5）计算求出：

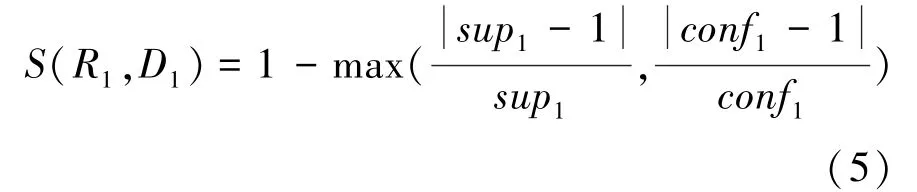
对于关联规则集相似度的计算，设存在关联规则集与某一时间段数据。其中，规则集包含若干关联规则R，为关联规则集规则数量，为某一时间段数据元素与关联规则集元素交集个数。关联规则集的相似度的计算可写为式（6）：

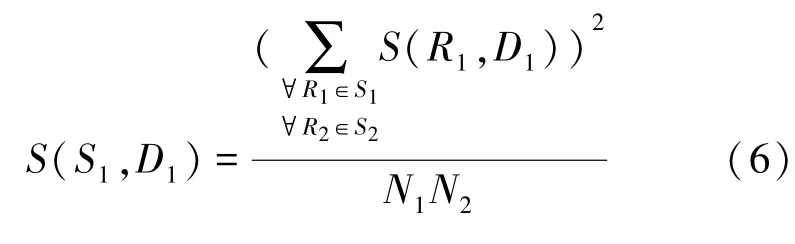
3 实验结果及分析

实验使用NSL-KDD网络流量数据，以评价RFPG算法异常检测的性能。实验环境为：64位的Win10操作系统，IntelCoreTM i7-9700kf CPU，主频3.6 GHz、内存32 GB；仿真编程语言为Python3.8。

3.1 数据集介绍

NSL-KDD数据集是改进KDD-CUP99的网络流量数据集，优化了数据集冗余和重复数据多的不足。数据为9个星期的网络连接数据，采集于模拟的某国空军局域网。

数据集有41个特征，包含网络连接特征和网络流量特征。标签列分为了2类：正常模式的标识类型（normal）和异常模式的标识类型（abnormal）。数据集共125 972条数据，样本分布见表2。

表2 NSL-KDD数据集样本分布Tab.2 Samples distribution of NSL-KDD dataset

3.2 评价指标

在异常检测中，误报率（）与漏检率（）通常是衡量异常检测算法的指标，而误报率与检测率是基于混淆矩阵的概念实现。混淆矩阵见表3。对此拟做探讨阐述如下。

表3 混淆矩阵Tab.3 Confusion matrix

（1）误报率。是指正常而被误判为入侵样本数占正常样本数的百分比，数学定义公式如下：

（2）检测率。是指异常而被误判为正常的样本数占异常样本数的百分比，数学定义公式如下：

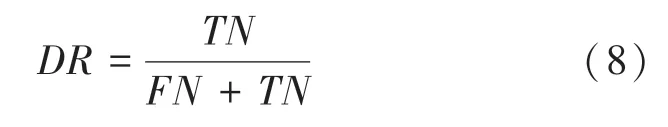
3.3 实验过程

为了模拟真实网络攻击状况、并检验RFPG算法异常检测效果，实验分别准备了3组不同数据量的数据，分别为：5 000条数据、10 000条数据、15 000条数据。每组中使用3类数据，分别是：包含5%异常样本数据的数据集；包含10%异常样本数据的数据集；包含15%异常样本数据的数据集。

实验中，RFPG算法使用前文求得的模糊聚类中心模糊化网络流量数据，按照先验知识将流量特征等数值特征_分为低、中、高三个模糊分区，并将连接特征等类别特征_按照其类型数量进行编码，研究获得（*_*_）个特征。其中，为模糊分区数，为类别特征包含的类别数。在挖掘模式强关联规则时，设最小支持度_08，最小置信度_08。

数据量为5 000、10 000、15 000时RFPG算法的评分结果曲线如图1～3所示。由图1～3可见，RFPG算法整体异常检测效果良好，并且随着数据量的提高，包含不同比例的异常样本数据的分类评分越稳定。由此证明：数据量越大，数据中包含的正常行为模式越完整，在挖掘关联规则时，实际为正常样本被预测为异常样本的概率降低，分类效果更好。由图3还可见到，RFPG算法实验结果中，包含不同比例异常数据的分类结果评分相近，证明该算法抗噪声干扰能力强，对于黑盒数据的模型泛化能力也很强。

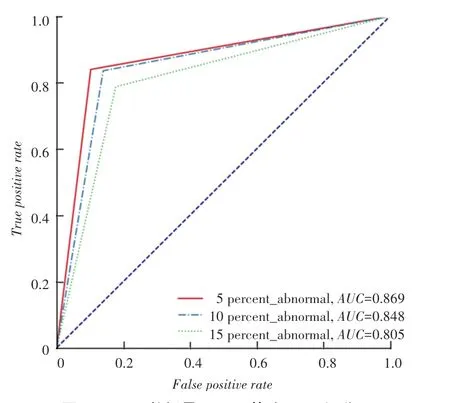
图1 5 000数据量RFPG算法AUC评分Fig.1 AUC score of RFPG algorithm when the amount of data is 5 000

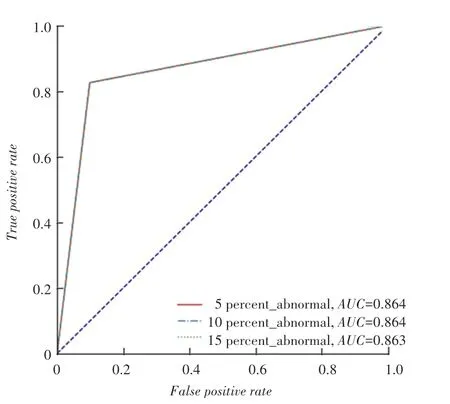
图3 15 000数据量RFPG算法AUC评分Fig.3 AUC score of RFPG algorithm when the amount of data is 15 000

3.4 对比试验

实验使用基于K-means异常检测算法、基于KL距离的异常检测算法、Fuzzy-Apriori算法以及RFPG算法进行结果对比。

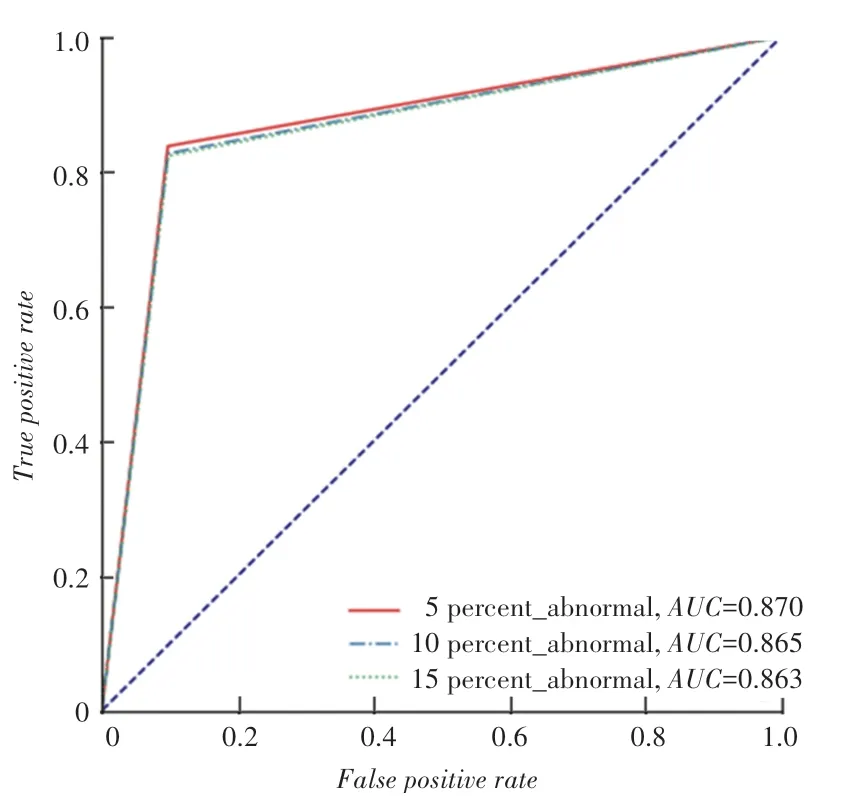
图2 10 000数据量RFPG算法AUC评分Fig.2 AUC score of RFPG algorithm when the amount of data is 10 000

对比实验选取同一包含15 000数据量以及10%异常样本的数据集，对RFPG算法的可用性进行验证，见表4。结果表明，在实验数据相同的情况下，RFPG异常检测算法相比其它算法，在误报率与检测率上都有着更好的检测表现。基于K-means的异常检测算法，对于数据特征变化偏移较小的异常数据容易产生漏检的情况；基于KL距离的异常检测算法，结合了EWMA预测模型刻画出了数据整体变化趋势，敏感性较高，有着较好的检测率，同时误报率也有所提升；Fuzzy-Apriori算法基于模糊理论，根据数据分布进行隶属度函数的建立，对于有标签的数据有着较好的表现，但是对于黑箱数据检测率与误报率表现欠佳，并且时间复杂度较高。RFPG算法基于bagging随机采样数据生成FP-Tree集合，得到长频繁项集合，并将其作为第二层的输入，生成近似正常模式的关联规则集，使算法面对黑盒数据依然有较为良好的表现，更符合异常检测的现实需求。同时，RFPG算法基于FP-Tree结构，使算法相较于Fuzzy-Apriori算法有着较优时间复杂度。实验结果显示，较高的检测率与较低的误报率也验证了RFPG异常检测算法的可用性。

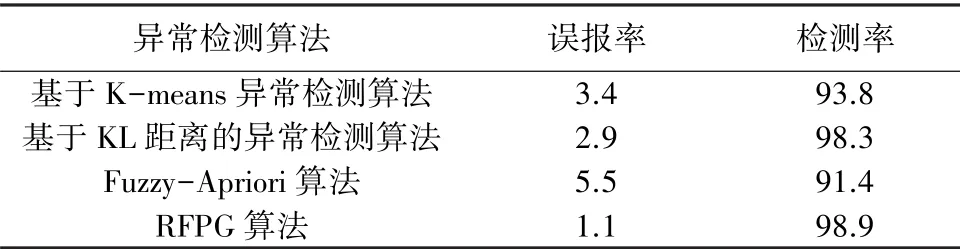
表4 多算法对比试验Tab.4 Algorithms comparison experiment %

4 结束语

本文提出的基于改进模糊FP-Growth异常检测算法RFPG，经实验表明，在大数据体量下，其异常检测能力更优，并且由于RFPG基于树的存储结构更适用于大数据集体量的场景，减少了提取关联规则集的运行时间和内存消耗。但基于先验知识，在对数值型特征进行模糊化处理时，会增加数据集的维度。因此，需要对自适应隶属度函数的建立，以及在算法过程中动态削减数据集维度与优化搜索空间进入深入探讨，以达到进一步优化整体异常检测质量与效率的研究目的。