基于蚁群算法的测试向量生成研究

康 鹏，金 婕，严 伟

（1 上海工程技术大学 电子电气工程学院，上海 201620；2 北京大学 软件与微电子学院，北京 102600）

0 引 言

随着电路板集成度和元器件复杂度呈现指数式增长，对其可控性、可测性和可观察性的要求越来越高，而对实践中电路板的测试要求也更加严格。传统的电路板故障检测方法都是以功能测试为出发点，步骤复杂，测试时间长，很难精确定位到故障点。为针对电子系统故障诊断的难点提供全面可靠的故障诊断方案，联合测试行动组（JTAG）提出了一套边界扫描体系结构标准化可测试性技术。边界扫描技术对待测电路发送测试向量，获取测试响应，通过测试向量和测试响应分析诊断电路故障。因此，在边界扫描的板级测试中，测试向量集的优劣直接影响故障检测的效果。如何生成高质量的测试向量集是当今边界扫描技术重点关注的问题。

近些年来，学者们提出了一系列的测试向量生成算法。如，改良计数算法MCSA、等权值抗误判算法、极小权值-极大相异性算法等等。这些算法建立在无限制故障模型的基础上，虽然有不错的故障误判率和故障混淆率，但是未能结合电路板的结构信息，难以实现最佳的测试效果。结构测试算法（Structural Test）通过分析电路板的结构和工艺信息，建立有限制故障模型，使得测试向量在具备完备故障诊断能力的前提下获得更小的紧凑性指标。基于近邻网络排序集的测试向量优化算法，虽然可以极大地优化测试向量集的紧凑性和完备性，但是受制于近邻网络排序集难以获取的特点，无法应用于工程实践。为此，本文提出一种有限制短路故障模型和蚁群算法相结合的测试向量生成策略。首先，结合PCB电路板的结构特征、元器件特性和工艺建立有限制短路故障模型，分析各网络间发生短路故障的概率。然后将问题转换成图论中最小点覆盖的问题，利用蚁群算法寻找最小覆盖点，结合网络近邻关系矩阵生成优化的测试矩阵，最后通过实验分析了该方法的有效性，最终生成的测试矩阵在保证完备性的情况下，具有较好的紧凑性。

1 有限制短路故障模型

对于包含个网络电路板的无限制故障模型，任意2个网络之间都会发生故障，故障类型分为固定逻辑故障和桥接短路故障。假定一个5网络的电路，研究时基于无限制故障模型的思想，可得到的拓扑结构如图1（a）所示。然而PCB板上的短路故障大多发生在元件管脚（焊点）、导线、过孔等之间，并且与其在PCB板的分布情况密切相关。因此，不同的2个网络之间发生短路的几率也是不相同的。另有研究表明，元器件管脚的焊点之间发生短路的几率和焊点之间的物理位置，可以用指数衰减函数来进行描述，对此可表示为：

其中，P、P表示电路板中的2个节点；表示节点之间的最短距离；表示两节点距离；表示两节点出现短路故障时的最大间距；表示距离最小的2个节点间出现短路故障的机率，1；表示衰减系数，1。

网络是由导线连接元器件管脚（焊点）构成的，对于一个有个网络的电路板，若n、n是其中的2个子网络，则n和n之间发生短路的可能性关系的数学表达式可写为：

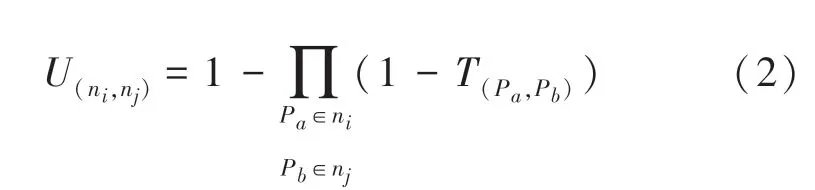
将式（2）简化成式（3）：

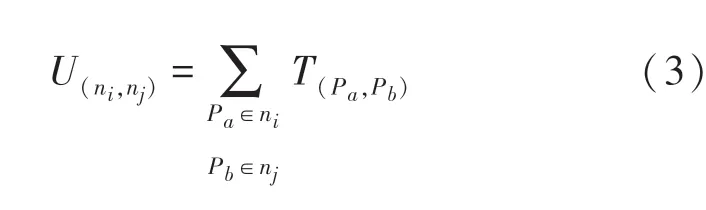
由式（3）计算出不同网络之间发生短路的几率。当小于阈值时，这2个网络不会发生故障。基于此理论，对于同一个5网络的电路板，结合电路板的结构信息，就可以计算出各网络之间发生短路故障的可能性。通过比较和阈值，可以将无限制的短路故障模型拓扑图简化成如图1（b）所示的模型图。

图1 网络短路故障关系拓扑模型Fig.1 Network short-circuit fault relationship topology model

2 蚁群算法

2.1 问题描述

边界扫描测试给每个网络赋予一个测试向量，通过采集并分析测试响应，即可推断出故障位置。在图1（b）中，如果能找到一个网络子集使得图中所有的边至少有一个端点在该子集中，那么由该网络子集组成的测试向量矩阵就可以诊断所有的短路故障。因此，可以采用求解图论最小点覆盖问题生成测试矩阵。

2.2 蚁群算法求解最小点覆盖

首先通过比较网络之间的短路几率和阈值的大小，确定对应边的权值，将无限制短路故障模型拓扑图G＝（，E）化简成有限制短路故障模型拓扑图（，），求有限制短路故障模型的最小点覆盖问题。根据蚁群算法的蚂蚁搜索原理，确定连接函数，函数定义式见式（4）：

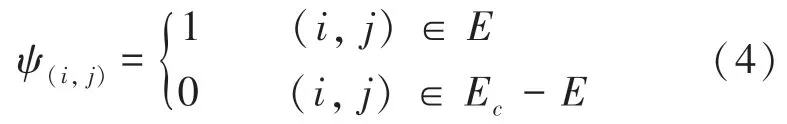
根据式（4）定义动态启发函数η，由此推得：

其中，ω表示顶点的权值。

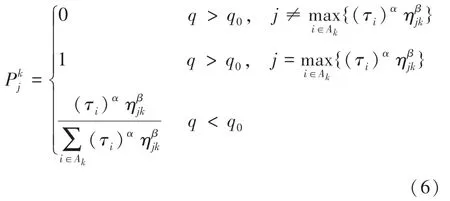
其中，表示启发式因子，该值越大，蚂蚁选择这个顶点的可能性越大，该值过小容易陷入局部最优解；表示期望启发因子；是标准参数；是随机变量，01。

蚂蚁在行走时会释放“信息素”，在最小点覆盖问题中，蚂蚁从一个顶点转移到另一个顶点是没有关联的，因此在蚂蚁选择新的顶点时需要进行更新局部信息素τ，推得的数学定义公式为：

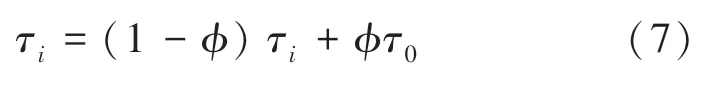
对于子集是否为全局最优解可用式（8）来判断：

当全部蚂蚁群完成所有路径后，全局信息素会进行更新，推导得到的数学公式可写为：

算法终止的条件是所有的蚂蚁结束循环，输出，选择不同的初始点，可以得到不同的覆盖集，比较得出最小点的覆盖集。

3 测试向量生成

为验证基于有限制短路故障模型和蚁群算法相结合的测试向量生成策略的可行性，方案流程如图2所式，以PCB电路板网络数23为例进行验证，通过Protel DXP软件获取电路板的结构信息网表，由式（3）计算各网络之间的短路可能性，通过阈值确定网络之间的权值，建立网络近邻关系如图3所示，并将其转变成布尔关系矩阵式，利用矩阵构造初始测试矩阵。与的数学定义公式分别如下：

图2 蚁群算法求解测试矩阵流程图Fig.2 Flowchart of solving the test matrix by the ant colony algorithm

图3 网络关系拓扑图Fig.3 Network relationship topological diagram

在初始测试矩阵中，“”代表了无效测试信息，第个列向量代表图3中n网络的测试向量，其测试向量中的第位用“1”表示。从图3中可知，网络与网络存在短路的可能，因此初始测试矩阵第一列中第2位属于有效的测试位，用“0”表示；然而在初始测试矩阵中第二列的第一位也用于检测网络与网络是否短路，造成了测试信息的冗余，需要利用蚁群算法求出最小点覆盖集，计算结果见表1。根据最小点覆盖集，对初始测试矩阵进行优化，选取初始测试矩阵中相关列向量，组成新的测试向量矩阵，最后还需确定矩阵中“”元素的具体值。为了满足检测固定逻辑故障的要求，最终确定“”值时，需要确保测试矩阵中没有全“0”或全“1”的行向量，一般通过合理的设定“”的值或增加列向量来满足测试要求。最终可求得测试矩阵：

表1 蚁群算法求解结果Tab.1 Ant colony algorithm solution results

4 性能分析

在生成的测试向量中，如果存在n和n短路故障特征向量与n无故障网络的测试响应相同，那么在对电路板进行测试时，就无法判断n和n网络之间是否存在故障，即故障征兆误判。此外，在测试向量中同样会出现n和n短路故障特征向量与n和n短路故障特征向量相同的情况，这样也会造成故障无法定位，即故障征兆混淆。

本文提出的测试向量生成方法，有效地结合电路板的结构信息，计算n和n网络之间出现短路故障的机率，若n和n网络之间不存在短路可能，就可降低故障误判率和故障混淆率。为分析本文测试向量生成方法的性能，采用等权值算法、极小权值极大权值相异性算法和本文的算法，依据不同网络数的电路板进行了仿真实验。传统测试矩阵生成算法与本文算法结果对比见表2。

表2 传统测试矩阵生成算法与本文算法结果比较Tab.2 Comparison of the traditional test matrix generation algorithms and the results of this algorithm

从表2中可以看出，在不同值条件下，本文提出的测试矩阵生成算法，在保证测试完备性指标和紧凑性指标的前提下，具有较低的故障征兆误判率和故障征兆混淆率。

5 结束语

本文在建立有限制短路故障模型的基础上，引入蚁群算法，能够快速、高效地获取被测电路板的最小网络覆盖集，以此生成测试矩阵。实验结果表明，在阈值假定的前提下，该方法生成的测试矩阵能在保证测试完备性指标的同时拥有良好的紧凑性指标，具有较强的应用价值。