一种有效神经网络训练优化方法

陈 青，杨晶东，王 晗，彭 坤

（上海理工大学 光电信息与计算机工程学院，上海 200093）

0 引 言

目前，卷积神经网络（CNN）已广泛应用于图像处理、语音识别、自然语言处理等领域，并取得了巨大成功。典型的CNN由卷积层、池化层和全连接层组成。卷积层和池化层能够自动提取深层特征和降维。然而，训练普通的CNN模型需要大量参数。Lécun等人提出的LeNets网络中，使用了大约1 M个训练参数。Krizhevsky等人在ImageNet竞赛中应用了包含60 M个训练参数的ResNet网络，并使用了数据增强，其中包括翻转、裁剪、亮度和对比度变换来增加数据量。Yuan等人提出了基于ResNet50的腮腺肿瘤CT图像分类模型，并加入北京DSG公司的数据脱敏策略，提高了预测性能。然而，脱敏方法只能消除CT图像的特征，不能模糊整个图像的背景。此外，1 000次训练和90%的测试集精度表明，模型的收敛速度较慢，并且出现了一定的过度拟合。Sun等人改进了ResNet50，其中包括23 602 051个训练参数，通过使用深度卷积生成对抗网络（DCGAN）的数据增强，对苹果品质进行分类化。这些操作可以为单个图像添加多个副本，以提高图像利用率和数据多样性，从而提升分类模型的性能。

然而，在同一数据集上进行多次训练后，具有大量参数的迭代会在一定程度上导致过拟合。训练集中的噪声也会对网络性能产生负面影响，导致泛化性能下降。通常使用随机梯度下降（SGD）算法训练网络参数，并使用正则化和指数移动平均（EMA）算法优化网络性能。具有综合自回归的传统移动平均模型（ARIMA）、指数加权移动平均模型（EWMA）主要适用于时变序列的估计，如股市趋势预测、风速预测或旅游兴趣预测等。Huang等人提出了正则化和重新初始化指数移动平均（ReEMA），用于更新目标跟踪中的目标模型。ReEMA施加惩罚以降低新生成目标模型的不可靠性，并使用重新初始化项来缓解退化水平，进一步应用正则化器来限制复杂性，表明了高效性和有效性。

上述EMA算法均使用固定的衰减率来更新网络参数，故而并不适合长时间、多步骤的深层神经网络训练。因此，本文提出了一种基于Tanh函数的动态衰减指数移动平均算法（T-ADEMA）。该算法以变系数Tanh作为衰减函数，动态自适应地调整模型参数，降低噪声。本文应用T-ADEMA算法对经典模型ResNet进行训练和测试，包括对MNIST、CIAFR_10、CIFAR_100数据集和当前流行的非CNN模型Vision Transformer（ViT）进行胸部X射线数据集的训练和测试，通过DCGAN算法进行数据增强。此外，还与传统的EMA算法进行了比较，分析了识别率和泛化性能。

1 动态衰减EMA算法

1.1 EMA算法

一组动态原始序列()由数据信号()和噪声信号()组成。其中，()是期望的测量值或有效信号，()是由噪声引起的随机信号。离散数据被视为一组时变数值序列，其表达式如下：

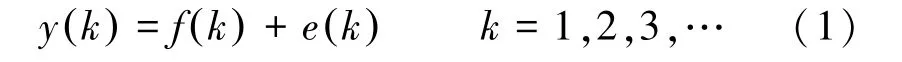
为了抑制()并提取()，通常对序列()进行平滑或滤波。对序列()进行适当的分段，在有数值振荡区间内，对一些合适的单元进行平滑和局部平均，以接近稳定区间，进一步削弱()引起的随机振荡。由于只选择了部分小区间进行局部平均和平滑，因此整个序列近似于()。假设有一组离散序列{，，，…，x}以及一组参数序列{，，，…，α}，∈[ 0，1]，经过加权移动平均优化，序列可由公式(2)得出：

其中，σ是序列x的指数移动平均值（EMA），α是指数移动平均值的权重。

在EMA的计算中，权重σ越大，EMA序列越接近序列x，平均效应越大，反之亦然。此外，由于权重序列项是恒定的，因此可以使用当前移动平均值及其之前的值来计算从到1的EMA。

1.2 动态衰减EMA算法

在神经网络训练中，每次迭代都会更新权重、偏移量和一些其它训练变量，以获得离散时间序列。假设神经网络模型的训练参数序列{，，…，ω}，则基于EMA算法同步更新的影子参数序列{，，…，v}可由公式（3）得出：

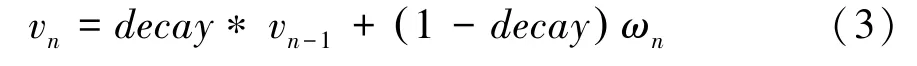
其中，是衰减率，按经验通常取值为09或099。

按递归方式逐项展开式（3），可以得出公式（4）：

其中，表示训练迭代次数，是一个常值参数，控制移动平均值，根据经验将其设置为09。可以看出，第个移动平均值只与序列{ω，…，ω}和衰减系数有关。在用SGD优化器训练网络参数的同时，选择合适的学习速率（本文中的学习速率设置为0.001），可以加快网络收敛速度，在一定时间内学习足够多的有效特征。基于以上原因，本文采用T-ADEMA算法更新训练参数，有效地消除了训练噪声，提高了泛化性能。

为了在神经网络训练过程中根据不同的训练阶段更有效地过滤噪声，本文基于公式（5）中ADEMA算法的衰减系数，提出了基于衰减系数的T-ADEMA算法，见式（6）。衰减系数应满足以下公式：

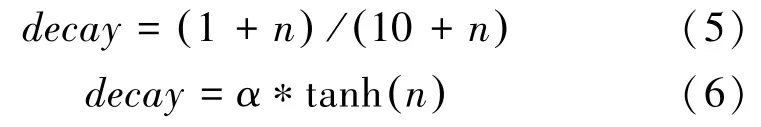
2 基于动态EMA优化的分类模型

由于本文实验图像数据集的分辨率低于ImageNet，因此该体系结构可以应用于ResNet网络。常见的ResNet网络由50层（包括池化层）和3个全连接层组成，每个层都有作为激活函数。

本文提出了基于动态EMA算法的T-ADEMA算法来优化训练参数的权重，并将其应用于图像分类。详细的模型结构和参数如图1所示。首先，将大小为3×224×224的原始图像输入残差网络模型。通过1和层后，输出图像的大小为645656。2_包含3个，每个包含模块（3层虚线）和模块（3层实线）。模块首先使用11卷积降低特征映射的维数，然后执行33卷积操作来提取特征，最后使用11卷积恢复维数。卷积层连接到（批量归一化）和层。模块用于深化网 络 结 构。2_、3_、4_、5_的数量分别为3、4、6和3。用于层 和层 之 后 的 分 类。和_10有10个分类。_100包括20类粗分类和100类细分类。用于每个全连接层的激活函数。全连接层的2层应用了以减少过拟合。输出层使用函数计算反向传播的误差，进而获得分类概率。

图1 基于T-ADEMA优化的残差网络结构Fig.1 The ResNet framework based on T-ADEMA optimization

图2展示了基于T-ADEMA优化的Vision Transformer（ViT）框架，其中原始图像被划分为16个切片作为输入特征图像。针对3分类的胸部X光图像，本文将基于T-ADEMA的ViT模型与其他主流的EMA优化方法进行了比较实验。

图2 基于T-ADEMA优化的VIT网络结构Fig.2 The VIT framework based on T-ADEMA optimization

3 实验预处理

实验使用的深度学习框架为Pytorch。实验环境包括Intel i7-10700 CPU、NVIDIA GeForce RTX 3070以及NVIDIA CUDA_CUDNN加速器、Windows 10 20H2和Python3.8｜Pytorch 1.7.0。

3.1 数据集

本文将提出的T-ADEMA算法结合SGD优化器在MNIST、CIFAR_10／100和COVID-19等4个数据集上验证其泛化性能。其中，MNIST是一个公开手写的数字图像数据集，由60 000个训练样本和10 000个测试样本组成。样本是28*28的二值图像，具体如图3（a）所示。CIFAR_10数据集是应用最广泛的图像识别数据集，由50 000个训练样本和10 000个测试样本组成，每个样本有28*28个像素，数据集拥有10个分类，如图3（b）所示。类似于CIFAR_10数据集，CIFAR_100数据集拥有100个类，包括每个类的500个训练图像和100个测试图像，如图3（c）所示。图3（d）展示的COVID-19数据集由3个类别的胸部X光图像组成，即COVID-19、正常、病毒性肺炎。COVID-19数据集的图像分辨率为1 024×1 024，共2 900例，这里的215例COVID-19，1 340例正常，1 345例病毒性肺炎。

图3 4个数据集的训练样本Fig.3 The training samples of four datasets

3.2 图像增强

实验中，对CIFAR_10／100采用传统图像增强方法，以提高识别率。将训练数据放入模型训练前，随机进行左右、上下翻转，亮度变换或对比度变换；对于COVID-19数据集，采用DCGAN对数据集进行增强和扩充。图4显示了DCGAN的批量增强和扩充过程。保留20%的3类比例原始样本用于测试集，剩余样本用于DCGAN进行数据扩充。DCGAN图像增强后的样本分布见表1。由表1可知，通过DCGAN分别生成3类图像样本，达到每个类别有1 200个样本。可以看出，在DCGAN算法的基础上，经过约200轮训练，增强后的图像与原始图像越来越相似，最终的增强图像在DCGAN算法的基础上取得了更好的效果。

表1 DCGAN图像增强后的样本分布Tab.1 Samples distribution after data augmentation via DCGAN algorithm

图4 COVID-19数据集的DCGAN图像增强Fig.4 The data augmentation via DCGAN algorithm on COVID-19 dataset

为了验证基于DCGAN算法的数据增强效果，采用分布随机近邻嵌入SNE，用来降低样本分布可视化的维数。SNE通过将高维空间映射为高斯分布概率，将相似性转化为相邻样本之间的概率。本文从每个类别中随机选取100幅真实图像和100幅通过DCGAN算法生成的图像，分别通过SNE进行可视化。原始图像和生成图像通过SNE可视化分布如图5所示。从图5（a）～图5（c）可以看出，生成图像（红点）的分布与原始图像（蓝点）的分布近似。可以推断，生成的图像与原始图像具有相似性，可以应用于样本分类。此外，图5（d）表明，每一类样本超过1／3的样本数是可分辨的，并且属于不同的类别。由此可以看出，DCGAN算法不仅学习了胸部X射线图像的全局特征，而且能够分辨出局部细小特征的区别，能有效地识别3类样本。

图5 原始图像和生成图像通过t-SNE可视化分布Fig.5 Distribution of real images and its corresponding generated images via t-SNE

4 实验分析

4.1 SGD＋T-ADEMA算法性能分析

为了验证EMA算法的有效性，分别在MNIST、CIFAR_10／100和COVID-19数据集上进行了对比实验，并使用SGD优化算法、固定衰减EMA算法（SGD＋EMA）、公式（5）中的动态衰减ADEMA算法、公式（6）中的动态衰减T-ADEMA算法（SGD＋T-ADEMA）和主流优化算法Adam等5种优化算法，在固定或动态学习率和批量训练的情况下，优化了ResNet50和ViT分类模型。MNIST训练集包含60 000个样本，批量大小为30，每轮训练包括2 000次迭代。由于模型经过5轮训练后接近收敛，因此每50次迭代计算一次训练集损失，以记录收敛参数。对于数据集CIFAR_10／100和COVID-19，在训练100轮左右后收敛，每次训练一个轮次计算训练集的损失。本文在5种不同的EMA算法上计算了5轮实验的评估指标均值，并分别训练MNIST，CIFAR_10／100和COVID-19数据集。评价指标包括准确率（）、精 度（）、召回率（）、值。研究推得的计算公式如下：

其中，、、和分别为真阳性、真阴性、假阳性和假阴性。

在MNIST数据集、CIFAR_10数据集、CIFAR_100数据集和COVID-19数据集上5种算法的损失函数和评估指标对比结果如图6～图9所示。图6（a）、图7（a）、图8（a）和图9（a）分别显示了5种优化算法在各数据集上的训练损失函数曲线。实验结果表明，在训练初始阶段，SGD＋T-ADEMA算法只学习到少量图像特征，并不能有效抑制小批量数据中的噪声，其收敛速度较慢，仅相当于ADEMA算法在较少训练回合中的平均值，在早期训练迭代中下降最慢。这是因为SGD＋T-ADEMA算法在滤除噪声方面效果更好，在早期训练阶段需要较少的学习数据，学习速度也相同，因此损失降低相对较慢，且该算法在经过多轮训练后能学习到更有效的特征。SGD＋T-ADEMA算法在训练中期，在MNIST和CIFAR_100数据集上收敛最快。虽然在CIFAR_10数据集的收敛速度略低于ADEMA，但可以过滤更多的噪声。在训练后期，SGD＋T-ADEMA算法的损失曲线的收敛性明显优于其他4种算法。在COVID-19数据集上，SGD＋T-ADEMA算法与其他EMA算法相比收敛速度更快。经过几轮训练参数的更新，学习了足够多的特征，有效地过滤了噪声。测试集上5种算法的评估指标见表2。

图6 MNIST数据集上5种算法的损失函数和评估指标对比Fig.6 The comparison of training loss and evaluation indicators of five algorithms on MNIST dataset

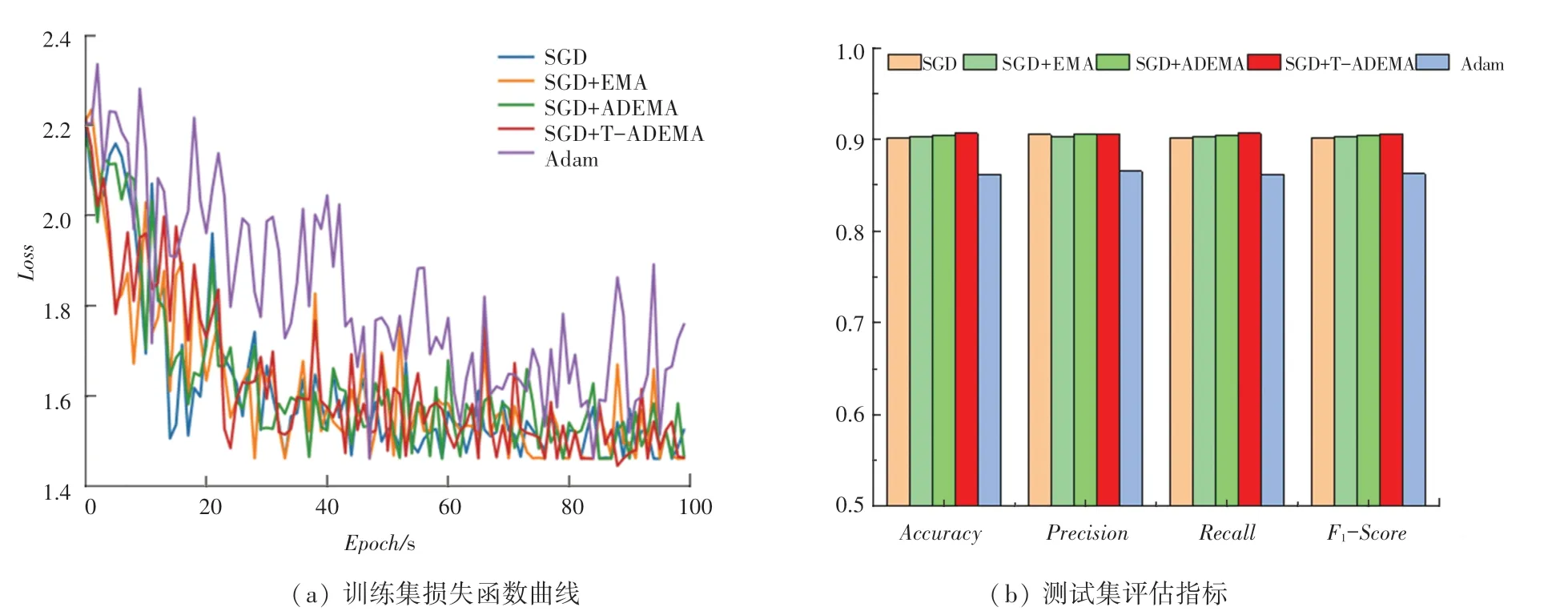
图7 CIFAR_10数据集上5种算法的损失函数和评估指标对比Fig.7 The comparison of training loss and evaluation indicators of five algorithms on CIFAR_10 dataset

图8 CIFAR_100数据集上5种算法的损失函数和评估指标对比Fig.8 The comparison of training loss and evaluation indicators of five algorithms on CIFAR_100 dataset

图9 COVID-19数据集上5种算法的损失函数和评估指标对比Fig.9 The comparison of training loss and evaluation indicators of five algorithms on COVID-19 dataset

由表2以及图6（b）、图7（b）、图8（b）、图9（b）可见，在上述4种数据集上的实验结果表明，SGD＋T-ADEMA模型的各评估指标均优于传统EMA算法和主流Adam优化器，数据集训练越困难，TADEMA算法就越有优势。此外，考虑到GPU内存（8 GB）的限制，本实验选择的最大批量为32，不同训练批量可能会提高模型的预测性能。

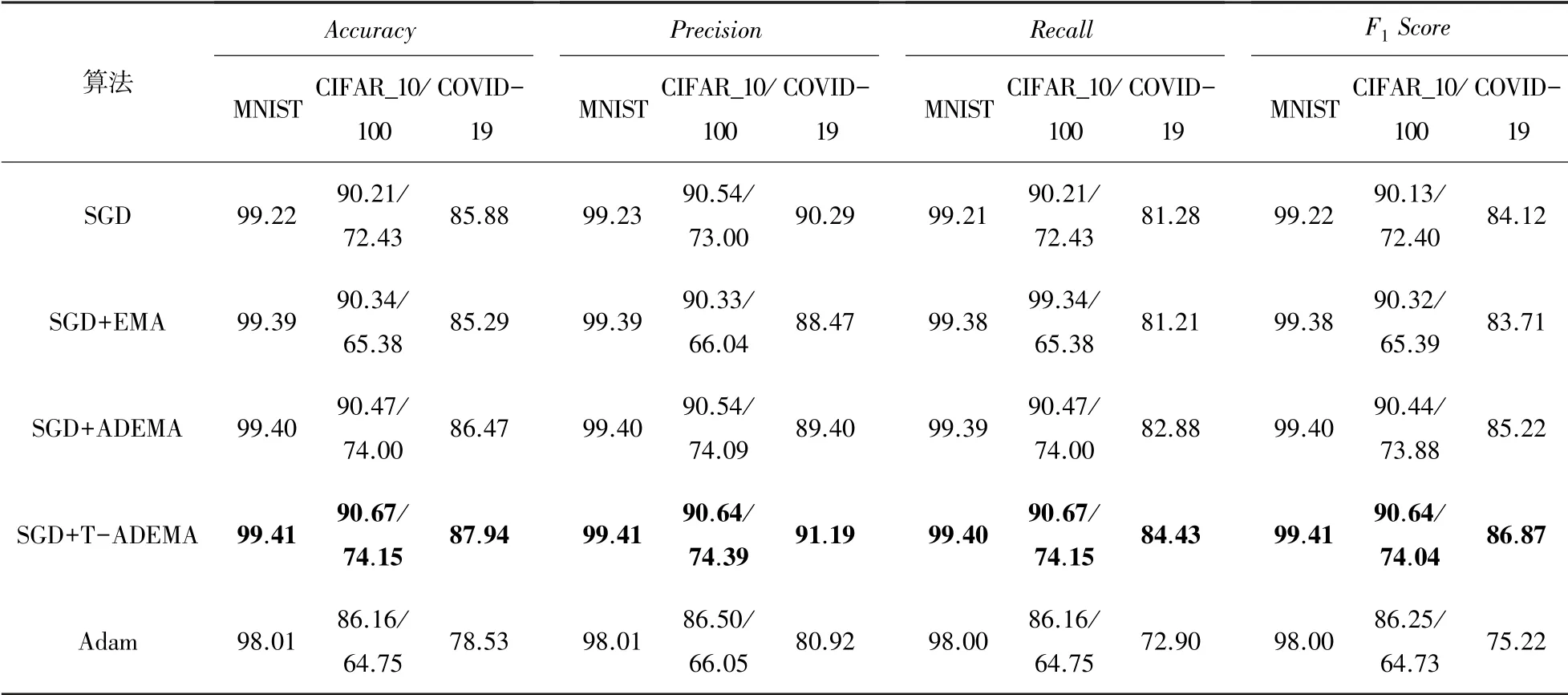
表2 4种数据集上评估指标对比Tab.2 Comparison of evaluation indicators on the four datasets

综上所述，动态衰减EMA算法比固定衰减的传统EMA算法更适合模型优化。其中，衰减系数决定了更新速度，衰减系数越大，网络收敛越稳定。当网络开始训练时，使用较小的衰减来确保初始学习的准确性，随着迭代次数的增加，衰减系数逐渐增大，可以有效地滤除噪声引起的无效学习，提高训练精度，使网络具有更好的收敛性。

4.2 T-ADEMA＋SGD算法实时性分析

为了分析本文模型的实时性，对5种优化算法在4个数据集上的训练时间进行了比较，其结果见表3。由表3中数据可知，与其它算法相比，由于T-ADEMA算法使用Tanh函数计算移动平均，因此基于TADEMA＋SGD网络每批训练时间增加约0.02 s，比其它算法需要更高的计算成本。然而，SGD＋T-ADEMA算法比主流的Adam算法需要更少的训练时间。虽然T-ADEMA算法的训练时间略高于传统算法，但可以有效地加快模型收敛速度，并在准确率、精度、召回率和值等评价指标上取得较高的精度。

表3 4类数据集训练时间对比Tab.3 Comparison of training time on the four datasets s

5 结束语

本文提出了基于动态衰减的T-ADEMA＋SGD算法更新模型训练参数，在一定程度上提高了泛化性能，加快了模型训练收敛速度。为了验证算法的有效性，将基于T-ADEMA＋SGD优化算法应用于ResNet50和ViT分类模型，用来优化各模型训练参数。实验表明，基于T-ADEMA＋SGD模型均能较好地提升各种样本库（如MNIST、CIFAR_10／100和COVID-19）的分类精度和泛化性能，对神经网络的训练和优化具有较好的启发意义。