基于PSSH电路的悬架系统馈能发电研究

2022-09-27张海龙

南京师范大学学报（工程技术版） 2022年3期

张晗,张海龙,马云

(南京师范大学南瑞电气与自动化学院,江苏南京 210023)

对于汽车这一高耗能高排放的产品,其保有量的逐年增加导致了国内石油消耗量居高不下. 为了追求更好的乘坐舒适性,提高行驶安全性,汽车的设计更加趋向高度自动化、集成化和智能化. 越来越多的驾驶辅助系统如驾驶员疲劳探测,自适应巡航控制,车道偏离预警,车道变道辅助,车道保持辅助,紧急制动系统和道路交通标识识别系统等应用增加车辆系统能源的消耗. 因此,为了响应国家节能减排的号召、提高汽车燃油利用率减小电动汽车的电池使用程度、提高车辆的续航能力,能量收集技术需要被逐渐利用到车辆设计中,从车辆中收集到的能量可以存储到电池中,也可以利用自供电技术为车载电子设备供电.

目前,众多学者对汽车悬架振动能量回收技术开展了广泛的研究,主要集中在对振动能量回收装置和能量回收转换电路两个方面. 可作为回收汽车振动能量的能量回收减振器主要分为两种:压电式和电磁式. 压电式能量回收主要是利用压电材料的压电特性,将挤压、拉伸、振动等机械运动应力或力转换为成比例的电势或电压[1],已经提出的悬臂式[2]、滚压式[3]和柔性关节式[4]压电振动能量回收装置可以用于乘用车上的振动能量收集. 电磁式能量回收利用电磁感应将机械能转换为电能,绕组的磁通量变化会在端部形成感应电动势. 电磁式能量回收装置结构多样,主要可分为直线电机式[5]和旋转电机式[6]. 由于能量回收装置所产生的电能往往是不能直接利用的,而标准能量回收电路[7]虽然结构简单适用性强但馈能死区大,回收功率不高,因此能将能量回收装置产出的电能高效地收集起来的转换电路对整个系统至关重要. 因为机电转换原理的不同,适用于压电式与电磁式能量回收装置的转换电路也会有所不同. 丁晓亮等[8]提出了一种改进型双中间电容压电式能量回收电路,经过理论以及仿真与实验验证,相同条件下该电路的最大回收功率为标准能量回收电路的8倍且回收功率与负载无关. Fang等[9]将最大功率点跟踪技术(maximum power point tracking,MPPT)应用到转换电路中来,实现了98.1%的最大MPPT效率. 汪若尘等[10]设计了一种应用在馈能直线电机上的转换电路,当电机感应电压较低时,能量虽然无法传递到超级电容中储存,但可以转化为电磁阻尼力以改善悬架性能达到能量再利用的目的.

本文根据馈能装置的结构原理,考虑到电磁式振动能量回收装置的死区特性,设计了一种新的电磁式振动能量回收电路即并联同步开关能量回收(parallel synchronous switch harvesting,PSSH)电路. 通过对该电路的工作方式进行详细的理论分析,推导出在恒定激励下的理论回收功率,建立仿真模型与标准能量回收电路进行比较,并进行实验验证. 结果表明,本文所提出电路能够在负载变化时一直保持着可观的回收功率,有着优越的性能.

1 悬架振动能量损耗与回收

1.1 悬架振动能量损耗

悬架振动能量回收潜力定性与量化研究一般从车辆能源损耗角度进行展开. 车辆在日常使用中燃油或电池能量仅有约15%用于动力推进和配件供能,其中大部分能量损耗于机械和传动机构以及克服阻力的过程中[11]. 以传统汽车为例,燃油能量损失主要为燃机的热、泵送与摩擦损失和车轮损耗[12],如图1所示. 考虑到车辆的能量平衡,车轮和减振阻尼器中粘滞环节共同消耗悬架振动能量,并随路面粗糙度和车速时变[13]. 因此悬架潜在振动能量一般可认为车轮滚动阻力损耗[14],占燃料能量损耗的3%～12%.

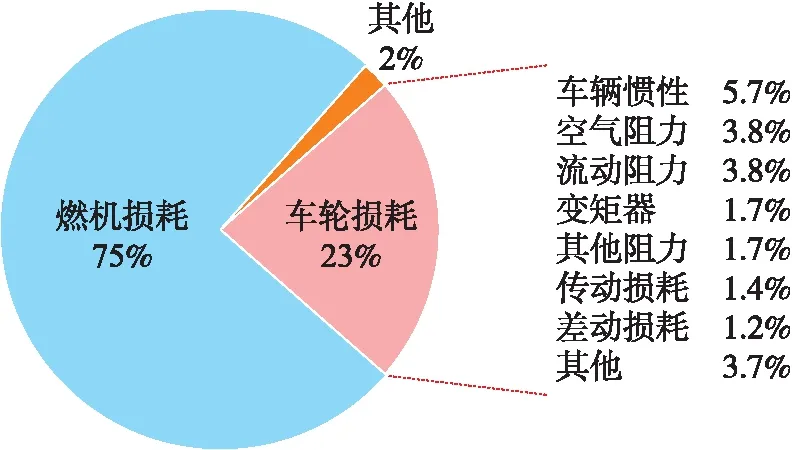
图1 车辆燃油损耗的各类能量损失占比

悬架振动能量有着可观的回收潜力,需要通过机电转换装置将它转化为电能以便存储和使用,目前回收悬架振动能量的装置主要分为压电式与电磁式两种.

1.2 振动能量回收模型

图2为二自由度车辆馈能悬架系统模型,主要由车厢、悬架弹簧、阻尼器、馈能电机与车轮组成. 定义系统参数:ms表示簧载质量,mu表示非簧载质量,ks表示悬架弹簧刚度系数,cs表示悬架被动阻尼系数或可变阻尼器等效阻尼系数,Fd表示阻尼器输出阻尼力,Fm表示直线电机轴向电磁力,kt表示轮胎等效刚度系数,ct表示轮胎等效阻尼系数,xi表示路面激励位移,xs表示车厢垂直相对运行位移,xu表示底盘垂直相对运动位移.假设:

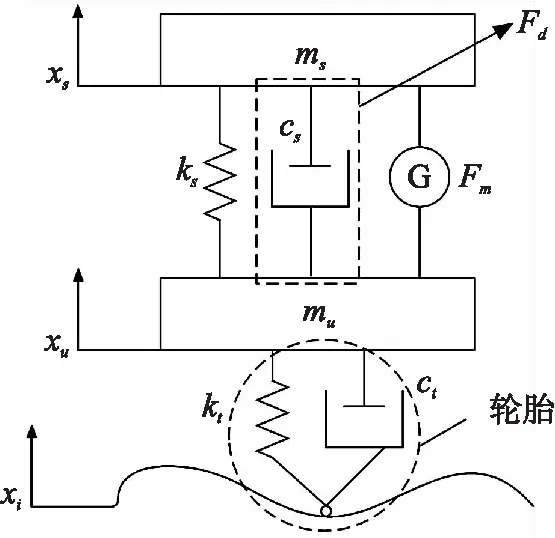
图2 车辆馈能悬架系统模型

(1)簧载质量与非簧载质量为刚体,仅有垂直于地面方向的运动.

(2)悬架系统具有线性刚度系数和阻尼系数.

(3)运动过程中阻尼器与直线电机均不超出有效行程.

(4)车辆轮胎始终贴合地面.

建立馈能悬架系统动力学模型

(1)

当馈能悬架系统阻尼器为传统被动悬架阻尼器时,输出阻尼力Fd可表示为

(2)

轮胎动态力为

(3)

不考虑馈能直线电机内部摩擦损耗,则馈能电机产出功率可表示为

Pm=Fm(xs-xu).

(4)

2 PSSH电路理论分析

本文提出了PSSH能量回收电路,如图3所示,PSSH能量回收电路由馈能直线电机、并联同步开关S1、整流桥D1～D4、电容C、开关S2、电感L、续流二极管D5、滤波电容CL以及负载RL组成.

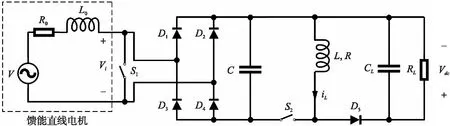
图3 PSSH能量回收电路原理图

该直线电机装置的振动能量回收电路是基于通过LC谐振将电荷转移的思想所提出的,具有很高的回收功率. 即使负载不同,回收的功率能够一直保持在很高的水平,具有比较好的负载适应性. PSSH振动能量回收电路在每个机械振动周期T内进行两次能量回收,每次能量回收可分为4个阶段. 第一阶段开关S1闭合、S2断开,电机输出电流增加,电机产生的电能储存在绕组电感L0中.第二阶段S1断开,储存在绕组电感中的电能通过绕组电感L0与电容C构成的LC振荡回路转移到电容C中,设此阶段电机输出电流经过四分之一个振荡周期后降为零时,感应电压也降为零的激励频率为临界频率fc.第三阶段S1、S2同时闭合,电容C中的能量通过和电感L构成的LC振荡回路转移到电感L中.第四阶段S2断开,电感L中的能量转移到负载RL中,实现半个周期的单次能量回收. 下面以馈能直线电机机械振动速度的正半周期为例对单次能量回收的4个阶段进行详细地理论分析.

设馈能直线电机机械振动速度u以正弦规律u=UMsin(ωt)变化,感应电压为V=VMsin(ωt).若感应电压频率低于临界频率fc,馈能电机运动速度u、馈能电机输出电流IL0、整流桥交流侧电压Vi、电容C两端电压VC、电感L电流IL、输出电压Vdc的波形如图4所示.

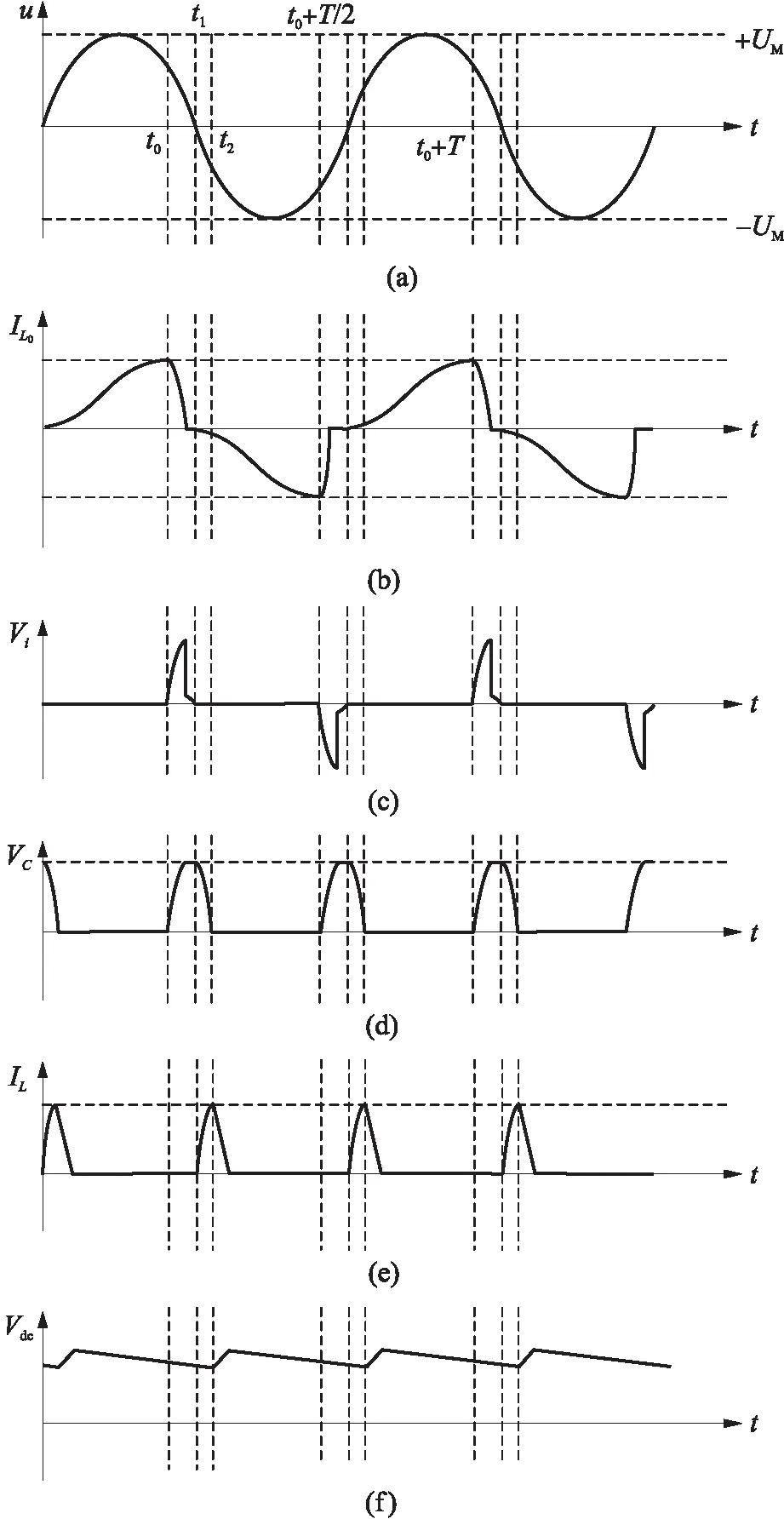
图4 感应电压频率小于临界频率fc时PSSH电路波形图

t0时刻之前为第一阶段,开关S1处于闭合状态,S2处于断开状态,馈能直线电机相当于短路状态,给直线电机内部绕组等效电感L0充能,根据基尔霍夫电压定律可得

(5)

将IL0的初值零代入上式可得

(6)

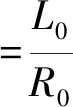
(7)

当L0储存的电能达到最大值也就是流过L0的电流达到最大值时为t0时刻,此时关断S1.第二阶段开始,由基尔霍夫电压定律

(8)

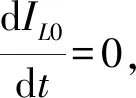
(9)

式中,ω0和ξ0分别是第二阶段振荡回路固有的角频率和刚度系数,其可以由下式表示

(10)

在电容VC达到最大值,电感L0电流降为零时,电路中没有电流流过,当振动频率低于临界频率fc时,馈能电机两端电压还未翻转,会有很短时间的开路电压,其值与等效理想电压源电压相同,是由于馈能电机还有很慢的正向速度,如图4中[t0,t1]段所示,当其降为零时,输出电压开始翻转.令dVC/dt=0可以得到此时电容C两端电压Vend,

(11)

在t1时刻开始第三阶段,馈能电机两端电压降为零,开关S1、S2同时导通,负半周的能量通过S1给绕组等效电感L0充电,与正半周类似.而储存在电容C的电能通过电容C与电感L构成的振荡回路转移到电感L中去,根据基尔霍夫定律

(12)

电感L上的电流可以表示为

(13)

式中,ωLC和ξLC分别是第三阶段振荡回路固有的角频率和刚度系数,其可以由下式表示

(14)

经过四分之一个振荡周期流过电感L的电流达到最大,此时电容C两端电压降为零,能量全部转移到电感L中.因为电阻R很小,所以刚度系数ξLC≤1,令dIL/dt=0可以得到电感L电流的最大值

(15)

在t2时刻开始第四阶段,电容C两端电压降为零,开关S2断开,电感通过续流二极管D5、负载电容CL给负载RL供电.由于负载电容CL和负载RL构成的RC电路时间常数2πRLCL远大于半个振动周期,近似将负载电压Vdc看作常数.可得

(16)

式中,电感L电流的初始值为Iend.由于R很小,R所占电压RIend≤Vdc,可忽略R的影响,则式(16)可表示为

(17)

第四阶段电感L中的电流IL=0时,第四阶段能量转移结束,电荷的变化为

(18)

所以整个系统半个周期内回收的能量为

(19)

根据式(15)、式(18)和式(19)得出

(20)

式中,γ为

γ=e-πξLC.

(21)

由于本文提出的PSSH电路在每个周期内进行两次能量回收,因此PSSH电路的回收功率P为

(22)

当振动频率刚好等于临界频率fc时,使得在第二阶段电容VC达到最大值也就是电感L0电流降为零之后,电路中没有电流流过,此时馈能电机运动速度刚好降为零,输出电压刚好为零,此时开关S1、S2同时导通,整个电路工作过程与上文分析类似.

当直线电机绕组电感L0的感应电压频率大于临界频率fc时,使得馈能电机速度方向发生翻转导致绕组电感L0的感应电压也发生翻转时,在第二阶段电容C两端电压VC未经过四分之一个振荡周期达到最大值,即绕组电感L0电流未降为零,如图5中[t0,t1]所示.可见,直线电机运动速度的翻转导致的反向速度会使得馈能电机两端电压下降,但由于反向速度很小,产生的反向电压也很小,而绕组电感L0上仍有很大的正向电压.故反向的速度对馈能电机的输出电压影响很小,整个馈能电机对外呈现的仍是正向电压,储存在绕组电感L0中的电能仍然可以继续向电容C中转移.在VC达到最大值即电感L0电流降为零时,此时开关S1、S2同时导通,馈能电机的速度不是从零开始增加,即理想电压源电压不是从零开始增加,会产生一个延迟角,设其为φ.

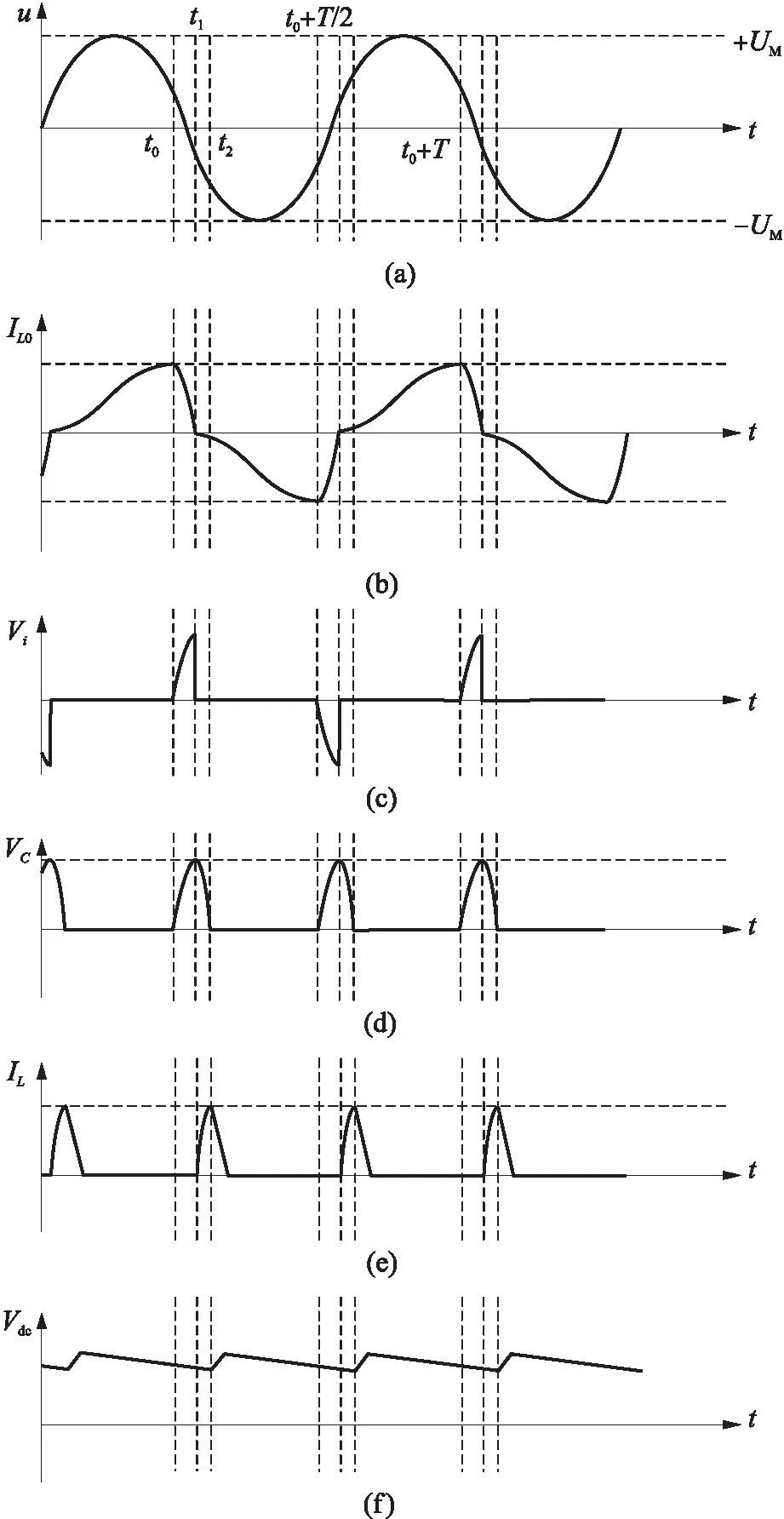
图5 感应电压频率大于临界频率fc时PSSH电路波形图

在这种情况下电路的工作方式略有不同,t0时刻之前为第一阶段,开关S1处于闭合状态,S2处于断开状态,馈能直线电机相当于短路状态,给直线电机内部绕组等效电感L0充能,此时由速度产生的电压为V=VMsin(ωt+φ).根据基尔霍夫电压定律可得

(23)

将IL0的初值零代入上式可得

(24)

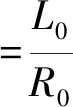
(25)

当L0储存的电能达到最大值,即流过L0的电流达到最大值,即t0时刻,此时关断S1,第二阶段开始,由基尔霍夫电压定律

(26)

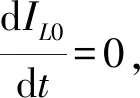
(27)

式中,ω0和ξ0分别是第二阶段振荡回路固有的角频率和刚度系数,

(28)

由式(28)可得第二阶段系统振荡周期T1,

(29)

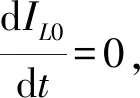
(30)

则可得延迟角φ,

φ=ωtφ.

(31)

由于振动频率大于临界频率fc,所以当电容VC达到最大值也就是电感L0电流降为零时速度方向已经翻转,所以此时只需要将S1、S2同时导通,开始电路工作第三阶段,储存在电容C上的电能通过电容C和电感L构成的LC振荡电路向电感L中转移.

3 电路仿真分析

3.1 仿真波形对比分析

首先对典型标准能量回收(standard energy harvesting,SEH)电路进行仿真,以正弦信号模拟馈能直线电机输出电压,图6为感应电压V、输入电流也就是流过电感L0的电流Ii、整流桥交流侧电压Vi以及负载端电压Vdc在感应电压幅值为6 V、频率为20 Hz下1 kΩ负载时的仿真波形图. 仿真时长设置为2 s,该时间与实际时间所对应,图中截取其稳定之后的一段. 从图中可以看出,当感应电压V小于负载端电压Vdc时,电路中无电流流过,整流桥交流侧电压Vi即为感应电压,当感应电压V大于直流侧电压Vdc时,整流桥导通,馈能电机输出电流IL0开始增加,整流桥交流侧电压Vi的幅值与负载端电压相同约为5.8 V左右,在感应电压V减少到与负载端电压Vdc相等时,输入电流Ii达到最大值约为0.046 A,经过一段延迟角后衰减到零. 可以计算得出SEH电路回收功率约为0.033 W.

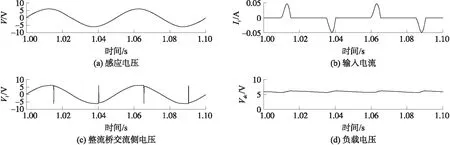
图6 SEH电路仿真波形

同样以正弦信号模拟馈能直线电机输出,图7为感应电压V、输入电流Ii、整流桥交流侧电压Vi、中间电容C两端电压VC、流过电感L的电流IL以及负载电压Vdc在感应电压幅值为6 V频率为20 Hz下1 kΩ负载时的仿真波形图. 仿真时长设置为2 s,该时间与实际时间所对应,图中截取其稳定之后的一段. 从图7 中可以看出,当感应电压V较低时,开关S1闭合,流过绕组电感L0的电流Ii增加.当流过馈能电机绕组电感的电流Ii达到最大值3.2 A左右时,开关S1断开,电容C两端电压开始上升,电容C两端电压达到最大值约为54.4 V后,待感应电压降为零,开关S1、S2同时闭合.S2闭合后储存在电容C中的电能通过一个LC振荡电路向电感L中转移,其振荡角速度由式(14)给出. 在这个阶段电容C两端电压下降,电感L电流上升,经过四分之一个振荡周期后电容C两端电压降为零,电感L的电流达到最大值约为11.8 A,此时关断S2,最终电感L中储存的能量转移到负载中,负载电压约为51.4 V,根据式(22)可以得到回收功率约为2.6 W远大于SEH能量回收电路.

图7 PSSH电路仿真波形

3.2 回收功率对比分析

图8给出了SEH能量回收电路以及PSSH能量回收电路在感应电压幅值为6 V频率为20 Hz激励下回收功率与负载的关系. 从图中可以看出在负载为1～1 000 Ω内变化时,SEH电路的回收功率随着负载的增大先增大后减小,所以SEH在最优负载约为2 Ω时有着最大回收功率约为2.6 W. 而单相PSSH电路的回收功率几乎不随负载的变化而变化,一直保持在2.7 W左右,既提高了回收功率等级又有很高的负载适应性.

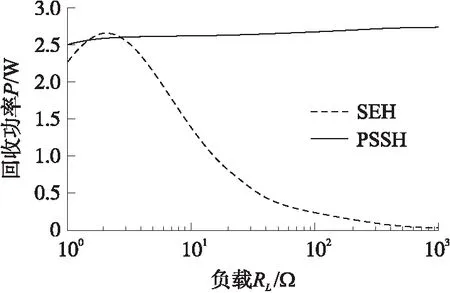
图8 回收功率与负载的关系

4 实验验证

本节将通过实验测得标准能量回收电路、PSSH电路在幅值为6 V频率为20 Hz正弦信号源激励下的实验波形和回收功率结果.

标准能量回收电路结构简单,在能量回收接口电路的研究中使用广泛,通常都把它作为其他电路的参考. 首先验证标准能量回收电路回收功率随负载的变化情况,实验中当负载为1 kΩ时,通过示波器将信号导入上位机中,得到输入电压V、整流桥交流侧电压Vi和负载两端电压Vdc的波形如图9所示. 从图中可以看出标准能量回收电路的实验波形与理论波形一致,用万用表测得该电路负载两端电压为4.44 V,通过计算可以得到回收功率为0.019 7 W.

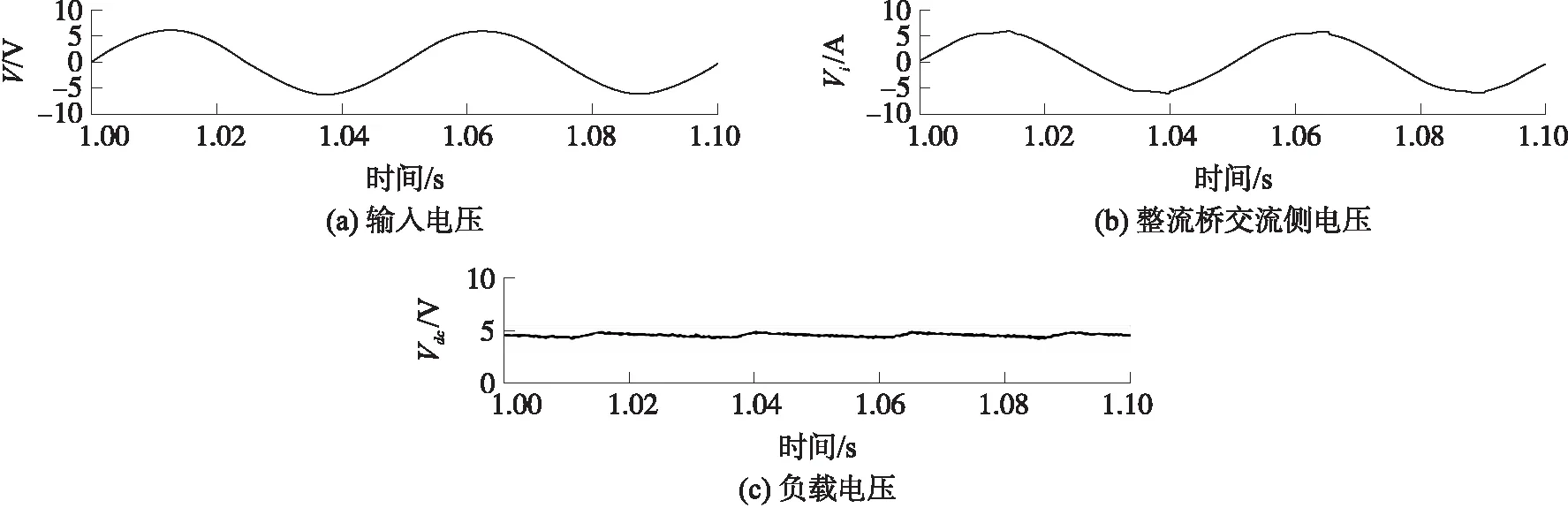
图9 SEH电路实验波形

当负载RL不同时,相应的回收功率也会不同,实验中选择负载从1 Ω到1 kΩ以对数规律变化,选取25个数据点,相应的测得其负载电压,得到负载电压与负载的关系图,如图10(a)所示. 再通过负载电压计算出相应的回收功率,得到回收功率与负载的关系图,如图10(b)所示. 从图10可见,随着负载的增大,该电路的负载电压也会随之增大,但是回收功率先增大后减小,最大回收功率Pmax约为1.405 W,对应的最优负载Ropt约为1.78 Ω.

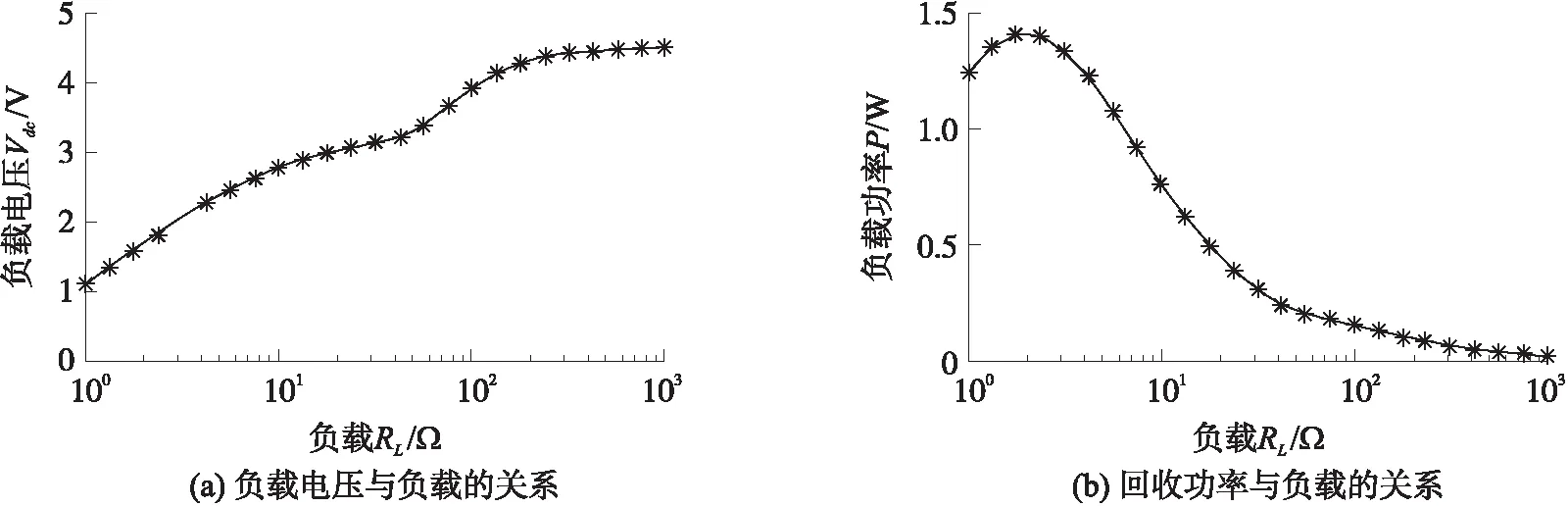
图10 SEH电路的负载电压和回收功率

当负载为1 kΩ时,通过示波器将信号导入上位机中,得到PSSH电路输入电压V、输入电流Ii、整流桥交流侧电压即开关S1两端电压Vi、电容C两端电压Vc以及负载两端电压Vdc波形如图11所示. 从图中可以看出PSSH能量回收电路的实验波形与理论波形一致,用万用表测得该电路负载两端电压约为50.24 V,通过计算可以得到回收功率为2.524 W.

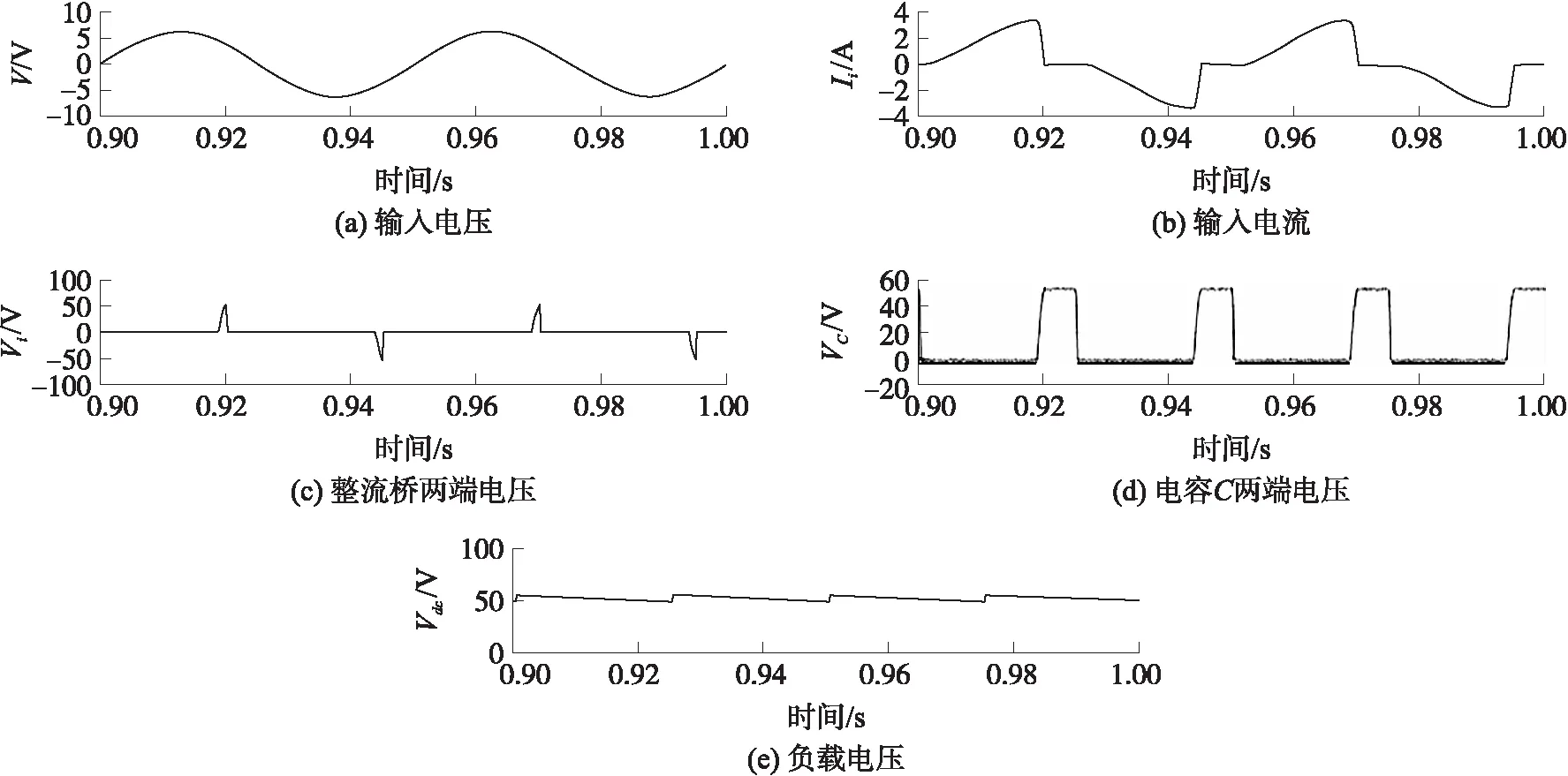
图11 PSSH电路实验波形

从图12可见,在负载较小时,PSSH电路负载电压随着负载的增大缓慢增大,当负载大于100 Ω后负载电压随着负载的增大迅速增大,呈现出抛物线趋势,与理论分析相符. 而随着负载电压的变化回收功率的变化则不明显,基本上维持在2.469 W左右.

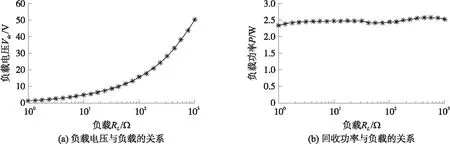
图12 PSSH电路的负载电压和回收功率

可以看出SEH电路实验中的负载端电压和回收功率与仿真相比低了很多,但PSSH电路实验中的负载端电压和回收功率与仿真相比相差不是很大,这主要是由实验中二极管的压降造成的,SEH电路整流桥交流侧两端电压幅值只有6 V左右,而PSSH电路在整流桥导通时交流侧电压幅值可以达到50 V左右,因此实验中二极管的压降对SEH电路回收功率的影响要比对PSSH电路回收功率的影响要大得多.