基于Levenberg-Marquardt算法的碳化硅MOSFET建模研究

赵奕昕,刘守城,颜 伟,祝志博,居 铭

(1.南京师范大学南瑞电气与自动化学院,江苏 南京 210023)(2.南京师范大学江苏省电气装备与电磁兼容工程实验室,江苏 南京 210023)

随着智能电网、汽车电子、航空航天、轨道交通和工业生产等领域电气化程度的不断加深,以 IGBT 和 MOSFET 为代表的功率开关器件被广泛应用于电机驱动、功率变换和能源传输等场合,作为核心器件,功率开关器件的特性决定着整个系统性能的好坏[1-3]. 当前大多数功率 IGBT 或 MOSFET 是硅基开关器件,然而,目前硅材料本身的性能已接近极限,因此传统硅基功率开关器件已经很难满足当前相关行业对器件在高频、高压、高温等极限环境下的要求. SiC MOSFET(Silicon Carbide metal-oxide-semiconductor field-effect transistor)以其优越的特性、较宽的禁带宽度、较高的耐压值、较好的散热效率以及较快的电子饱和漂移速度等特点受到业界和国内外学者的广泛关注. 但目前碳化硅开关器件成本较高,迭代速度快,在系统初期设计阶段为了评估功耗、效率以及电磁兼容性能等关键指标,需要建立快速精确的静态与动态仿真模型[2-3].

近年来,国内外学者在功率MOSFET建模方面展开了多方面研究. Duan等[2]提出了一种基于EKV数学模型的功率MOSFET的电热行为模型的快速建模方法,考虑了封装寄生参数,对其静态和瞬态行为进行了仿真,并分析了开关过程和开关损耗. 李川[3]详细分析了理想与非理想情况下的SiC MOSFET动态特性,并对非线性电容进行静态特性建模,利用微分状态方程描述了开关过程的每个阶段,分析了器件动态开关行为. 许明明等[4]在EKV模型基础上增加了一个温控电压源,改善了高温下模型的准确度. 文献[5-6]指出原EKV模型温度的自由度较低,器件在不同温度下的静态特性难以同时拟合,使用改进的通用静态模型后拟合效果与误差得到改善. 文献[7-9]通过对比基于曲线描点和参数模板、基于库文件、基于物理公式和基于数学公式的4种不同建模方法,指出通过数学公式得到的模型精准度最高,且更容易考虑温度参数.

由此,本文针对CREE公司的碳化硅MOSFET功率器件(型号:C2M0080120D)进行开关行为建模与分析,建立其静态模型和动态行为模型. 对于静态模型,利用麦夸尔特法进行参数曲线拟合,对器件转移特性、输出特性和寄生非线性电容进行建模. 对于动态模型,分别建立器件导通和关断过程每一个阶段的栅源极电压、漏源极电压、肖特基二极管电压、栅极电流和漏极电流的电路微分方程组,再以每一个阶段结束时的状态变量作为下一个阶段的初始条件,求解上述电路微分方程组的数值解. 最后,与LTspice软件的仿真波形进行对比,验证模型的准确性.

1 静态模型建模分析

MOSFET静态模型包括在不同结温下的器件转移特性曲线(Id-UGS)和输出特性曲线(Id-UDS),以及 3个寄生非线性电容(CRSS,COSS,CISS)随漏源级电压(UDS)的变化曲线,本文采用Levenberg-Marquardt算法进行非线性曲线拟合,实现静态模型的建立.

1.1 Levenberg-Marquardt算法

最优化算法——牛顿法的基本思想是在目标函数的某点使用泰勒展开,舍去除梯度矩阵f和黑塞矩阵H之外的高阶项,通过多次迭代搜索目标函数最小值.

(1)

由于牛顿法存在计算量大、非正定黑塞矩阵、奇异矩阵不能求逆、不能保证目标函数值下降、不能保证收敛等缺点,需进行修正优化.Levenberg-Marquardt算法属于对牛顿法的优化修正,其迭代公式为

xk=xk-1-αk(H+μI)-1f(xk-1).

(2)

对于非正定黑塞矩阵,新定义一个矩阵K=H+μI,其中μ为阻尼系数,I为单位矩阵,由此可保证矩阵K可逆.Levenberg-Marquardt算法同时具有梯度法和牛顿法的优点,当μ很小时,相当于朴素牛顿法,当μ很大时,相当于梯度下降法,是一种介于牛顿法与梯度下降法之间的最优化方法.

将Levenberg-Marquardt算法修正的牛顿法应用于非线性拟合时,其最优化目标函数为

(3)

式中,f为需要进行拟合的目标函数,β为f需要拟合的参数矩阵,x和y为实际观测值矩阵,f(x;β)为模型预测值矩阵.定义残差矩阵r=f(x;β)-y,表示模型预测值和实际观测值的差值.

计算梯度和黑塞矩阵并代入,Levenberg-Marquardt算法迭代公式最终可表示为

βk+1=βk-(JTJ+μI)-1JTr.

(4)

式中,J为雅可比矩阵.

本文采用Levenberg-Marquardt算法进行曲线非线性拟合的流程图如图1所示.

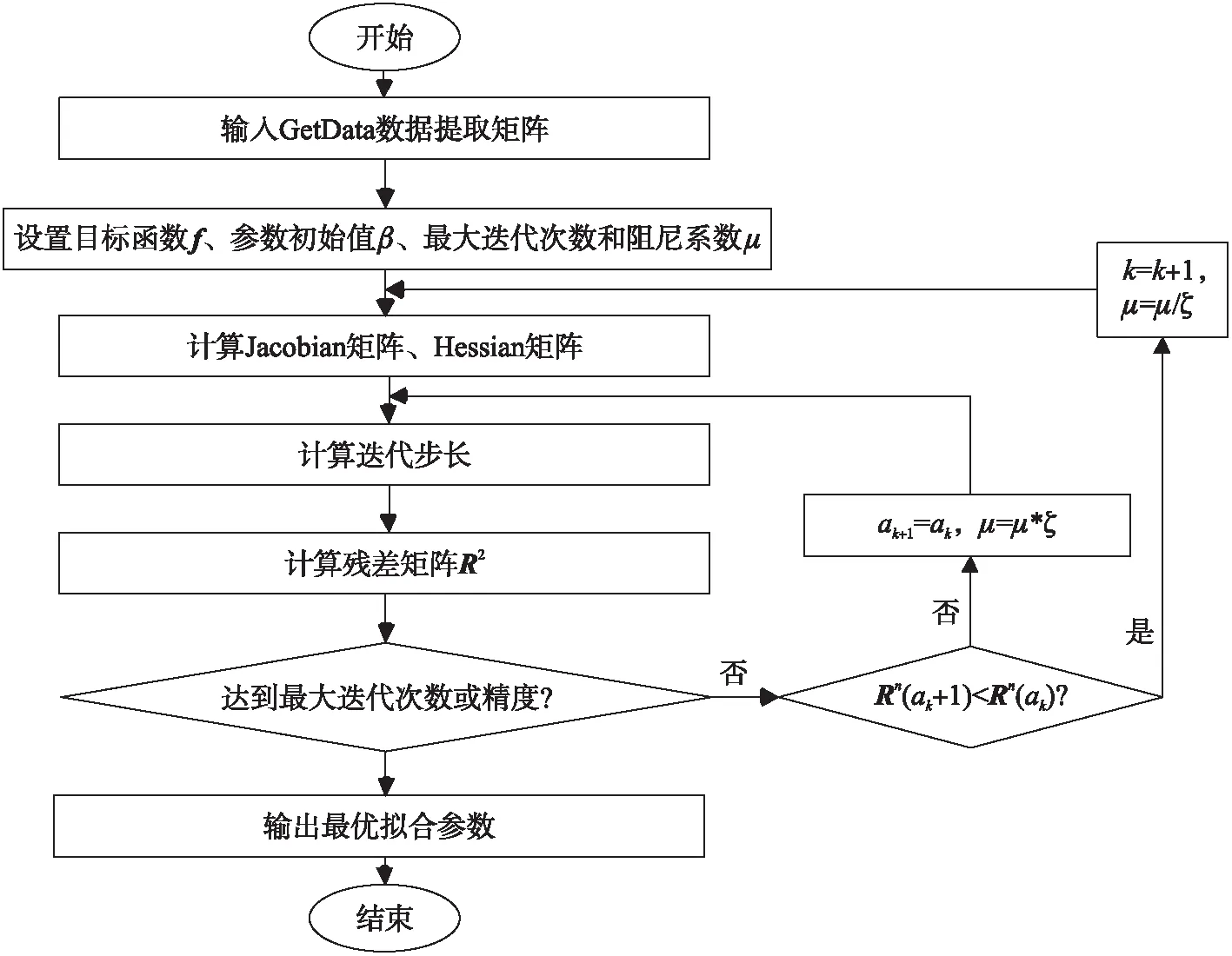
图1 Levenberg-Marquardt算法流程图

1.2 基于原EKV模型的建模

EKV模型使用两个对数函数的线性组合在两个操作区域之间插值,生成一个单片模型. 文献[1]提出的静态模型原理图如图2所示,采用一个EKV表达式,

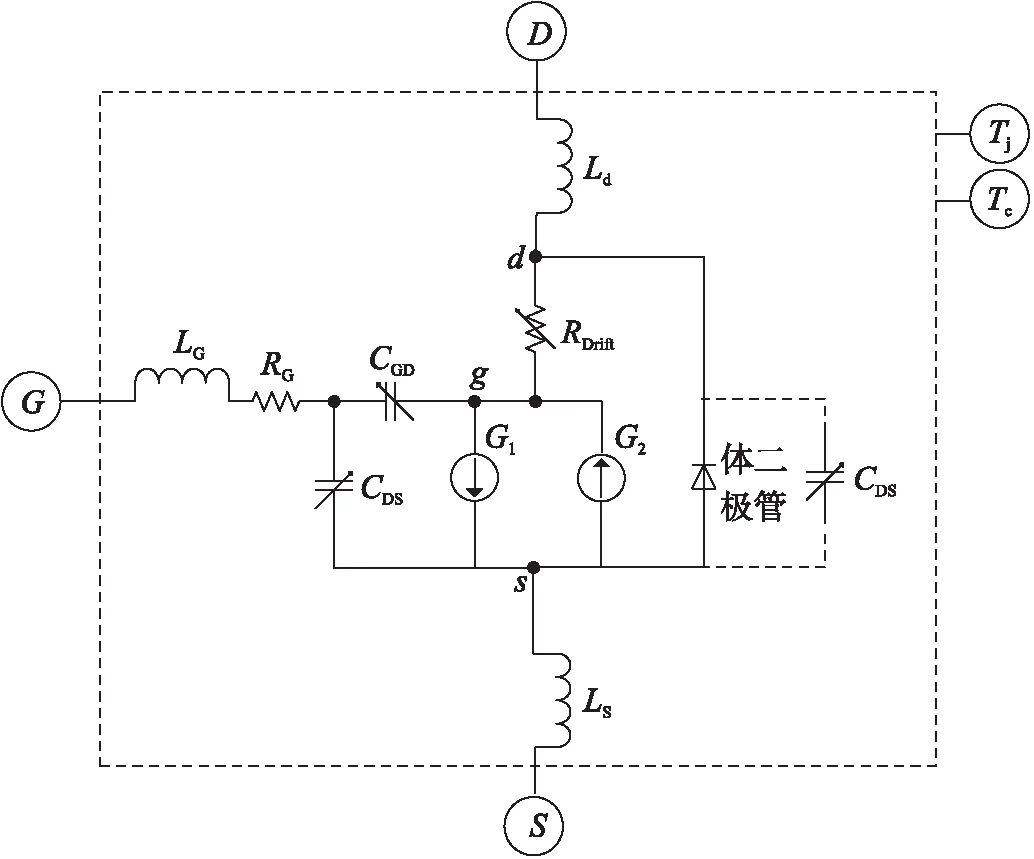
图2 模型原理图

(5)

式中各参数定义见表1.在不同温度下对SiC MOSFET的转移特性和输出特性进行拟合建模.

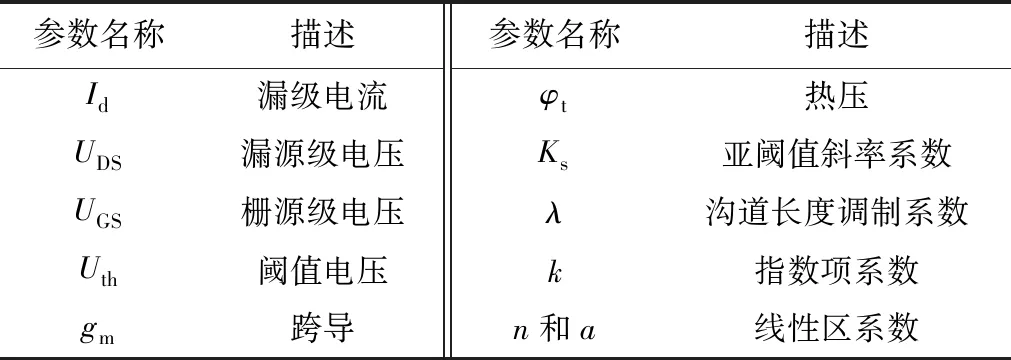
表1 EKV公式中参数

根据C2M0080120D的器件手册,该器件采用TO-247-3 封装,器件的电路模型如图2所示,G、D和S分别为栅极、漏极和源极;Tj和TC为结温和壳温;电感LG、Ld和LS为TO-247-3封装的栅极、漏极和源极的寄生电感;CGD和CGS为栅漏极和栅源极寄生电容;RG为栅极电阻;二极管结电容CDS为漏栅极寄生电容;G1和G2为压控电流源.

在每个温度下器件的转移特性曲线有1条,输出特性曲线共有6条;在上述7条曲线中,对每条曲线使用GetData软件均匀取25个点,组成漏极电流Id、漏栅极电压UDS和栅源极电压UGS矩阵.再以上述矩阵为数据源,式(5)为拟合函数,使用Levenberg-Marquardt算法进行拟合.拟合时需要将上述 7个数据矩阵一起导入算法,提取共同的gm、φt、Ks、λ、k、n和a参数值,并将其代入式(5),从而实现MOSFET静态模型的建立.拟合结果与数据手册对比如图3.

图3 拟合结果对比

拟合结果图3的拟合参数结果和误差结果分析见表2,从拟合结果与数据手册对比图3以及误差分析表2可以看出,该静态模型能够对7条输出特性、转移特性曲线进行拟合,但无论是从对比图还是误差数据来看,拟合曲线不能完全贴合数据手册给出的曲线,结果表明该模型拟合误差较大,需要更精确的模型来描述MOSFET的静态特性.

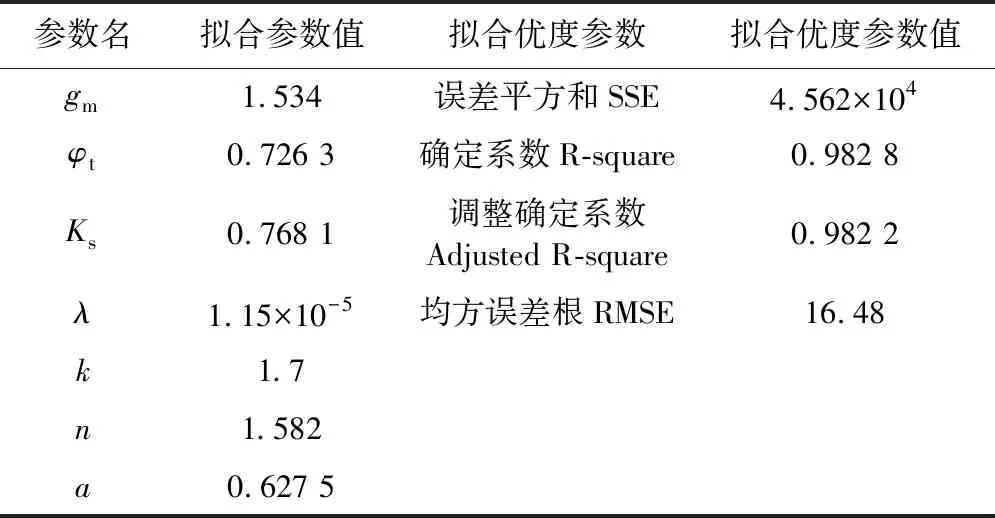
表2 拟合参数结果与拟合优度

1.3 改进的EKV模型

原EKV模型需要在已知UGS和UDS前提下求解Id,因此需要先给定一个初值,并在小步长下进行多次迭代才能求得Id近似解.在求解过程中,电流Id会存在虚数解,漏极电流Id解空间在UGS和UDS较小区域中会出现空缺,影响拟合精度[9-10].因此,需要对原模型进行改进:使电流表达式Id变成UGS和UDS的显式函数Id=f(UGS,UDS),已知UGS和UDS即可直接求得电流,无需进行迭代,其表达式为

(6)

式中,k1～k7为模型参数,与器件参数与结温Tj有关,其中k1对应跨导斜率,k2对应UGS系数,k3对应阈值电压,k4为指数项,k5对应饱和系数,k6对应UDS系数,k7对应UGS系数.

1.4 模型验证

为验证改进的模型对比原模型在收敛性和拟合精度上更有优势,将上文中提取25 ℃下的7条静态特性曲线组成的漏极电流矩阵Id、漏栅极电压矩阵UDS和栅源极电压矩阵UGS再次使用Levenberg-Marquardt算法进行拟合,拟合公式采用式(6),拟合效果如图4. 拟合参数结果与误差结果分析如表3.

图4 拟合结果对比

表3 拟合参数结果与拟合优度

从图4和表3可以看出,改进的模型拟合效果较好,拟合结果的确定系数达0.999 2,拟合曲线能够较好地贴合从DataSheet中提取的数据点,相对于图3有明显的优化.

图5为式(5)和式(6)模型的拟合解空间对比图. 在式(5)模型中,电流Id会存在虚数解,漏极电流Id解空间在UGS和UDS较小区域中会出现空缺,如图5(a)的右上角. 相较于图5(a),图5(b)中从手册中提取的数据点(黑色圆点)与解空间平面有较好的贴合,原先的空缺区域消失.

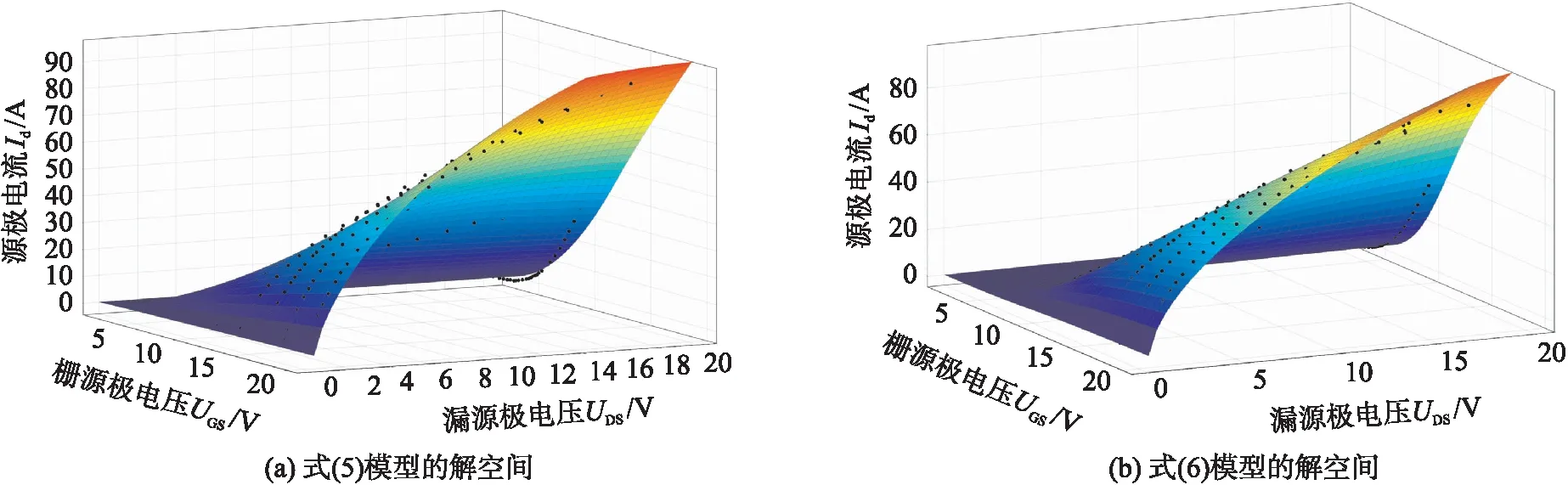
图5 三维拟合空间对比

从图4、图5和表3可以看出,基于式(6)的静态模型建模方法更为精确再现了碳化硅MOSFET器件手册中转移特性曲线和输出特性曲线.

实际情况中,碳化硅MOSFET存在寄生非线性寄生电容(CRSS,COSS,CISS). 根据器件手册,这些寄生电容值会随着电容两端的电压变化而变化. 在高频环境下,若不考虑这些电容值的非线性变化,在分析 MOSFET 开关行为时会产生较大误差,因此,非线性电容的建模对于后续章节的动态行为模型的精确建立意义重大.

非线性电容的建模也可采用曲线拟合的方法,不同的参考文献提出的电容拟合公式不尽相同. 根据器件手册上的3条电容曲线,其形态类似于反比例函数,故本文提出的拟合公式

(7)

式中,V为源漏极电压,p0、p1、p2、p3为模型系数.

使用GetData软件对数据手册中的3条非线性电容曲线每条取12个点,同样使用Levenberg-Marquardt算法进行拟合,拟合结果如图6,可以看出拟合结果较好.

图6 非线性电容拟合结果

另外,还需要计算寄生电感参数. 文献[10]采用TO-247-3封装的SiC MOSFET寄生电感可由有限元分析软件ANSYS的Q3D工具进行提取,栅极G,源极S和漏极D的3个寄生电感提取值如表4.

表4 基于Q3D的寄生电感

2 动态行为模型建模分析

SiC基器件相对于Si基器件工作频率更高,在提升系统响应速度的同时也带来了较高的di/dt和dv/dt,使得系统更加敏感,对杂散寄生参数的影响不可忽略不计. 这不仅会使器件开关过程中电流和电压尖峰幅值增加,还会引发振铃现象、器件误触发和自激振荡等隐患. 因此,碳化硅器件动态行为模型不仅需要考虑电路结构,还需要结合静态模型考虑寄生参数[10-14].

2.1 双脉冲测试电路

图7为进行开关行为建模分析的双脉冲测试电路原理图,结合静态模型,考虑了器件寄生参数的影响,加入了3个寄生非线性电容、3个寄生电感Ld、Ls、Lg以及1个寄生电阻Rd. 其中,Ld表示漏极寄生电感,Ls表示源极寄生电感,Lg表示栅极寄生电感,Rd表示测试回路中的寄生电阻,Csk表示肖特基二极管的结电容.

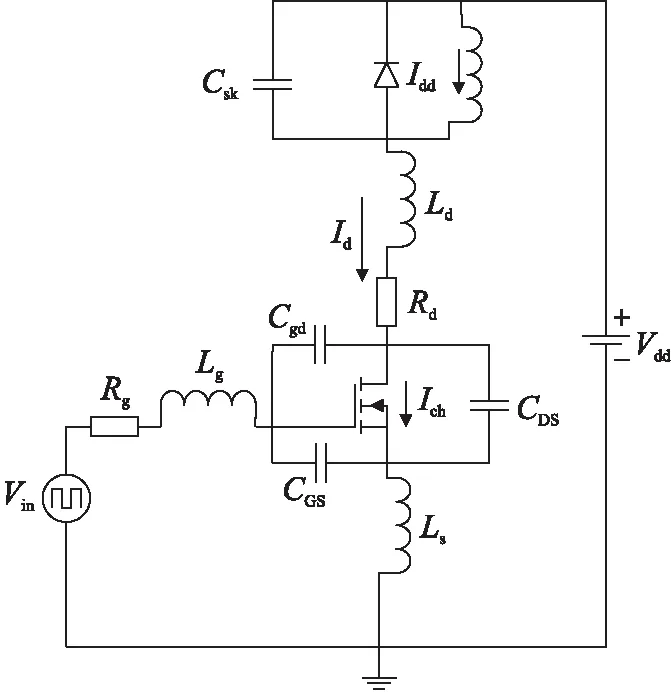
图7 双脉冲测试电路

2.2 开关过程分析与建模

在静态模型的基础上,分别建立MOSFET开通和关断过程每一个阶段的5个状态变量——栅源极电压UGS、漏源极电压UDS、肖特基二极管电压Usk、栅极电流Ig和漏极电流Id的电路微分方程组,达到每一阶段的结束标志时再以每一个阶段结束时的状态变量作为下一个阶段的初始条件,采用4阶Runge-Kutta算法对常微分方程组求解数值解,即可得到5个状态变量的时域响应曲线[15-16],从而实现MOSFET动态行为模型的建立. 开关过程可分为8个阶段[3],每个阶段描述及结束标志如表5所示.

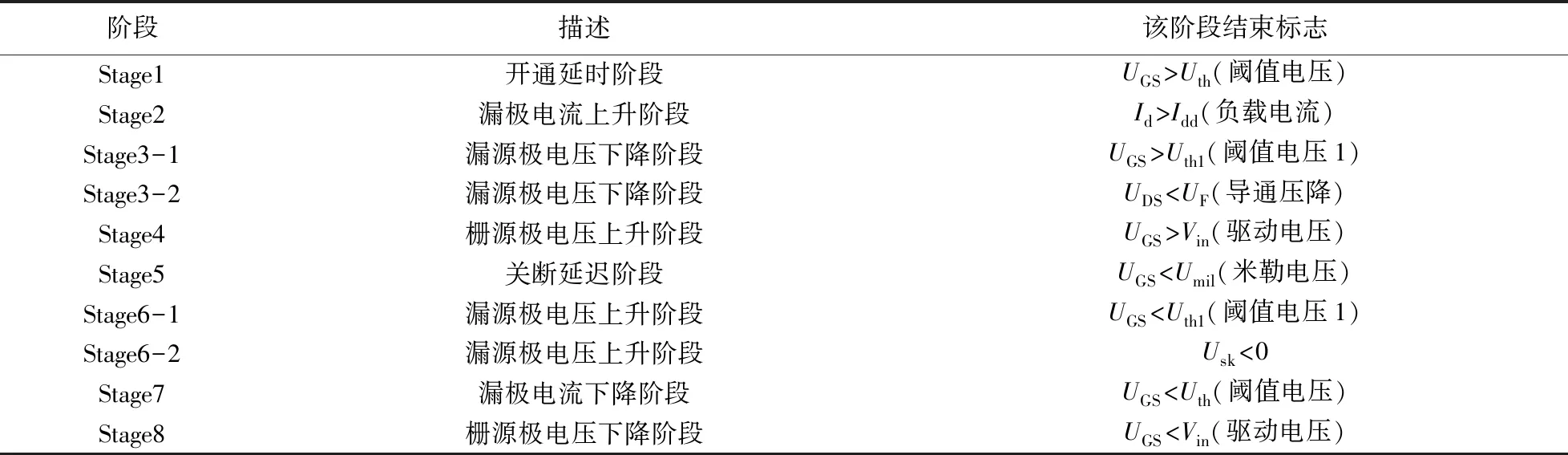
表5 开关过程分阶段描述

本文以Stage3-2阶段为例,Stage3-1结束时,漏级电流Id已上升到负载电流Idd=5 A,栅极电流Ig接近0 A,漏源极电压略小于Vdd,为724.73 V,根据图7和基尔霍夫电压电流方程可得

(8)

(9)

UGS=Ugd+UDS,

(10)

(11)

Stage3-2开始后,负载电流Idd全部从续流二极管中转移到MOSFET,续流二极管处于关断状态,二极管的寄生电容Csk开始充电,同时,漏源极电压UDS开始下降,直到器件完全开通,可得

(12)

(13)

联立式(8)-(13)即可得以x=[UGS,UDS,Usk,Ig,Id]为状态变量,形式为dx=Ax+B的状态方程.

进行动态行为建模时,还需考虑非线性电容(CRSS,COSS,CISS)随两端电压变化而电容值的不同,在求解每个阶段的微分方程组时,3个非线性寄生电容取值采用第一章中静态模型建立的3个非线性电容拟合公式,即联立微分方程组dx=Ax+B和电容拟合公式再进行求解.对状态方程联立电容拟合公式使用Runge-Kutta算法进行求解,当达到结束标志时,读取此时刻的时间t,以及每个状态变量的值作为下一阶段的初始值.

2.3 模型精度验证

为了验证所建立的动态行为模型的准确性,将图7电路在LTspice仿真软件中进行搭建,LTspice软件仿真得到的UDS、Id波形与动态行为模型UDS、Id波形结果对比图如图8(a)和8(b)所示.

图8 LTspice仿真与模型结果对比

从图8可以看出,对于电压UDS波形,器件关断时LTspice仿真波形上升到800 V后还会继续超调到850 V左右,而后振荡着下降到800 V,动态行为模型的电压波形能正确反应电压的超调、振荡和幅值变化. 对于电流Id波形,动态行为模型的电流波形能正确反应器件开通时的电流高频振荡与超调以及器件关断时的电流大幅振荡并最终降为零的过程. 因此,所建立的动态行为模型结果波形与LTspice仿真波形贴合良好,能正确反应器件开关过程的电压电流上升下降趋势,较好地贴合开关过程中电压电流的幅值和频率,也能正确反应开关过程的波形震荡及振铃现象,模型精确度较高,但仍有一定的优化空间.

对于其他实际应用电路,例如DC-DC电路,在分析其动态开关行为时,可基于图7双脉冲测试电路的分析步骤,根据实际电路拓扑结构与基尔霍夫电压电流方程,并考虑寄生参数,分别建立MOSFET开通和关断过程每一个阶段的各个状态变量组成的微分方程组,求解即可得到开关波形.

3 结论

本文建立的碳化硅MOSFET静态和动态行为模型,可以快速准确地对碳化硅MOSFET功率器件进行开关行为预测与分析. 对于静态模型,采用改进的EKV数学模型,基于Levenberg-Marquardt算法进行参数拟合,准确描述了器件的转移特性和输出特性,并验证了一种新的寄生非线性电容模型,建模速度快,模型误差小. 对于动态模型,在考虑封装寄生电感和寄生非线性电容等非理想条件下,分别建立器件导通和关断过程每一个阶段的栅源极电压、漏源极电压、肖特基二极管电压、栅极电流和漏极电流的电路微分方程组,再以每一个阶段结束时的状态变量作为下一个阶段的初始条件,采用4阶Runge-Kutta算法求解上述微分方程组的数值解. 最后,与LTspice软件仿真波形进行对比分析,结果表明上述建模方法能较好地描述器件的动态行为特性,对于估算碳化硅功率MOSFET器件在不同场合的开关损耗与开关波形具有重要指导意义,也可为碳化硅MOSFET行为级模型应用电路的搭建奠定基础.