考虑风速影响的双馈风机调频建模及稳定性分析
2022-09-27李永刚贺梦娟刘静利
李永刚,贺梦娟,刘静利,晋 飞
(1.华北电力大学电力工程系,保定 071003;2.国网潍坊供电公司,潍坊 261021)
风力发电因环境效益好、可再生、装机规模灵活、成本低等优势,在世界范围内快速发展,成为最具竞争力的新能源发电技术。然而双馈风力发电机DFIG(doubly-fed induction generator)作为风力发电市场的主流机型之一,其并网连接方式造成转子转速与系统频率解耦,风机对外弱惯量特性,缺乏对系统频率快速响应和主动支撑的能力[1-3]。随着局部电网风电渗透率的提高,系统的调频能力和抗扰动能力明显降低。许多国家和地区纷纷发布并网导则明确提出并网的风电机组要具备类似常规机组参与系统调频的能力[4-5]。
为使风电机组提供功率支撑,主动参与系统调频,国内外学者已开展大量研究,提出了一些成熟的控制方法,例如采用附加下垂控制的调频策略,模拟同步发电机一次调频有差调节过程,使风电机组具有频率下垂特性,有利于维持系统频率稳定[6-7]。但下垂控制不具备同步机的动态特性,对电网的惯性响应和频率支撑能力不足[8]。传统同步发电机具有天然的并网友好性,若并网逆变器具有类似于同步发电机的运行特性,就可满足风电友好并网要求。基于这一思路,诸多学者提出了虚拟同步机VSG(virtual synchronous generator)控制[9-11]。VSG根据传统同步机的机械与电磁方程来模拟惯量与阻尼特性,使并网逆变器从运行机制和控制外特性上与传统同步机相似。引入虚拟惯量可以减慢频率变化速度,增加一次调频时间,但同时可能引发功率振荡问题,恶化系统稳定性[12-13]。文献[14]通过建立下垂与VSG 控制小信号模型、状态空间模型,分析得出引入惯量使VSG 控制比下垂控制在频率稳定性方面更有优势,但加剧了输出功率的振荡。当前对风机调频控制的稳定性研究,多集中于控制器自身参数对频率及功率振荡的影响,风机实际运行条件对控制器的影响尚需进一步讨论。
实际运行中风电功率存在波动性和不确定性,风电机组初始工作点运行状态会影响风机的动态调频过程[15-16]。在变化风速下风电机组的实时可用容量不同,采用固定的下垂系数不利于调频效果和系统稳定性[17]。针对这一问题,文献[18-19]通过调整高、中、低风速区间的下垂系数整定方法,利用变下垂系数控制策略来协调不同风速下风机调频能力的差异。文献[20]利用建立的VSG 控制DFIG 系统在有功功率不平衡驱动下的内电势相位运动方程,分析了工作点运行状态对其惯性响应能力的影响。为适应多工况,克服风机运行状态对系统调频特性的影响,文献[21]分析不同风速下DFIG能量与虚拟惯量的关系,根据自身调节能力确定机组参与系统调频的方式,自适应调整运行状态。目前,运行状态对调频特性影响的研究多集中在单一调频控制方式。针对风机运行工况对下垂控制和VSG控制在调频能力和系统稳定性影响的对比研究相对较少,进一步分析风速变化与风机惯量及一次调频能力的耦合关系,对风机在不同运行工况下调频控制策略的设计具有一定的工程价值。
本文首先分析DFIG 的频率响应原理,对比研究下垂控制和VSG 控制的有功-频率调整机理;其次,评估DFIG 在不同运行风速下可参与调频的能量,确定临界风速所在风速区间,并在此基础上建立包含工作点运行风速的DFIG调频控制系统的小信号模型,推导出风机系统等效惯量与运行状态的耦合关系,对比风速对VSG和下垂控制调频性能的影响,确定VSG 控制的临界振荡风速计算公式;最后,利用DIgSILENT 搭建了含高比例风机并网系统的仿真模型对理论分析进行验证。
1 DFIG 的频率响应原理
1.1 DFIG 基本控制原理
与常规同步发电机组相比,DFIG 的转速变化范围(一般为0.7~1.2 p.u.)更宽,调频所需能量同样源于转子旋转动能,且更具可控性[22-23]。DFIG 基本控制原理如图1 所示,主要包括空气动力学模型、轴系传动模型,以及相应的转速、桨距角、调频、调压控制系统。

图1 DFIG 基本控制原理Fig.1 Schematic of basic control of DFIG
风力机将风能变为机械能的过程是一个涉及空气动力学、流体力学的复杂过程,但是当主要考虑风电机组电气特性时,一般可以采用简化的建模方法建立风电机组的空气动力学模型。风力机捕获的风功率可表示为

式中:Pm为输入机械功率;ρ为空气密度;R为风轮半径;CP(β,λ) 为风能转换效率系数;λ为叶尖速比;vw为风速;ωr为风机转速;β为桨距角。
对于任一桨距角,都有相应的最优叶尖速比λopt,使得捕获的风能最大化。因此,当输入风速vw变化时,风机的角速度相应调整以保持最优的叶尖速比,即运行在最大功率点跟踪MPPT(maximum power point tracking)模式,此时初始运行点风机转速可表示为

式中:λopt为最优叶尖速比;ωr0、vw0分别为风机参与调频时刻初始风机转速和初始风速。
假设以单质量块模型表征DFIG 轴系动态,则系统的轴系系统模型为

式中:H为DFIG 机械系统固有惯性时间常数;Pout为输出电磁功率;Tm、Tout分别为机械转矩和电磁转矩。
为了使DFIG机组具备与同步发电机相似的频率响应能力,源于转子动能的DFIG 机组的下垂和VSG控制方法已被广泛关注[24]。
1.2 下垂控制和VSG 控制原理对比
下垂控制通过模拟同步机一次调频的功-频静态特性,使逆变器根据电网频率及电压变化调整输出功率[6]。为了进一步提升风机的友好并网能力,同时考虑惯量和阻尼的VSG 控制使风电机组可以完全表现出同步机外特性,通过引入传统同步机二阶运动方程和励磁方程来实现频率和电压的调整[10]。下垂控制和VSG控制的原理如图2所示。
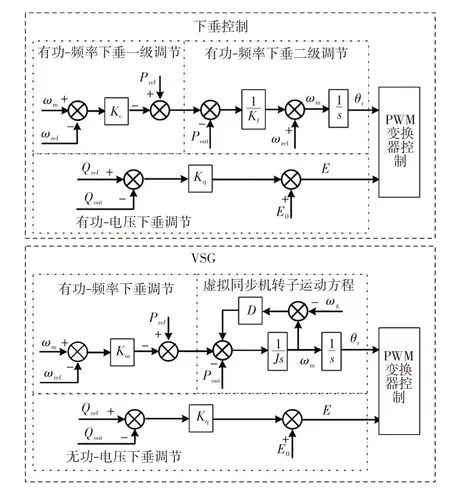
图2 下垂控制和VSG 控制原理Fig.2 Schematics of droop control and VSG control
本文对下垂控制和VSG 控制的有功功率频率调整部分进行对比分析。
下垂控制的基本思想是模拟同步发电机的调速功能,通过有功和频率的比例关系获取稳定的频率,其控制方程为

式中:Pref为有功功率参考值;ωm、ωref分别为系统输出角频率与角频率参考值;Kc、Kf分别为1级和2级功率/频率下垂控制系数。
图2 中,根据传统同步发电机转子运动方程和调速器方程可得到VSG有功-频率控制方程,即

式中:Kω为VSG有功-频率控制系数;ωg为系统角频率测量值;J、D分别为虚拟惯性系数和阻尼系数。
当Kc+Kf=Kω时,下垂控制方程可表示为

可以发现,当J=0、D=0时,若Kc+Kf=Kω,则下垂与VSG控制方程等价。
由于锁相环技术的局限性导致存在较大偏差,系统角频率测量值ωg可用角频率参考值ωref代替。将式(5)化简可得
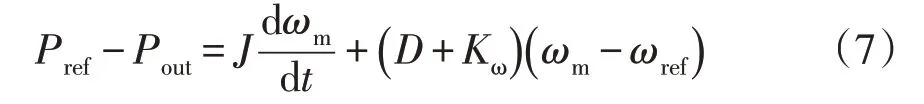
由图2 和式(4)~(6)可知,当VSG 控制的虚拟惯性系数J和阻尼系数D都取0 时,两种控制方式等价,所以VSG控制可以看作是一种含有惯性和阻尼的下垂控制。
2 基于风速的DFIG 调频控制系统建模
2.1 不同风速DFIG 有效调频动能分析与评估
由式(3)和式(4)可知,VSG和下垂控制均通过跟踪系统频率变化,利用对转子动能的控制实现频率调整。当系统负荷增大引起频率下降时,通过降低转子转速释放转子动能,向系统短时输出更多的有功功率,为系统提供频率支撑,待系统频率恢复稳定后,使转速重新恢复到最优转速。风机调频效果及运行稳定性取决于风机最大可释放动能与实际动能释放量的共同作用。
因机组动能变化量与机组初始运行状态相关,在下垂控制或VSG控制参与调频阶段时,通过释放风轮动能来提供的有功功率支撑,即

式中:ΔED为风机调频释放的风轮动能;JD为风机转动惯量;ωr0为风机参与调频时刻初始风机转速;ωr1为频率跌落至最低点时的风机转速。
转子转速范围一般为0.7 p.u.≤ωr≤1.2 p.u.,最大功率跟踪控制运行曲线如图3所示,划分运行区间如下:①低风速区(vw0≤6.4 m/s),转子转速为最小值ωr_min;②中风速区(6.4 m/s <vw0<11.0 m/s),风能转换效率系数CP恒定且最优,风速与转子转速呈正相关;③高风速区(vw0≥11.0 m/s),转速达到最大值ωr_max,风速增大转子转速保持恒定[25]。
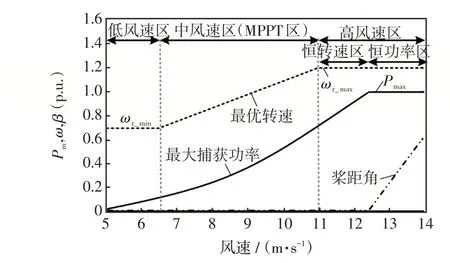
图3 DFIG 功率跟踪控制运行曲线Fig.3 Power tracking control curve for DFIG
由于机组不同运行工况转子转速不同,导致储存动能也不同,根据风机转速下限ωr_min计算出不同初始风速区间风机可释放的动能极限ΔED_max为
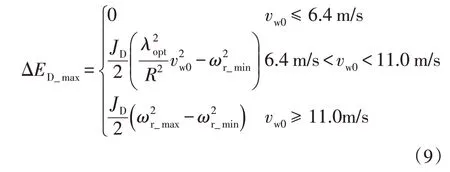
由转子动能的控制原理可知,转子动能的调频能力受制于风机的转速极限。根据风机在不同区间的动能释放量,可得调频策略在不同风速区间的调频能力如表1所示。

表1 风机控制策略调频能力分析Tab.1 Analysis of frequency modulation capability under fan control strategy
当处于低风速区时,ΔED_max为0,系统受到扰动后风机会因过度释放动能导致转速过低而失稳;当处于高风速区时,风机转速达到最大值,可用容量达到最大,若在此区间系统实际释放动能大于最大可释放动能,则在任意风速下系统都不稳定,即控制参数设置不合理。
2.2 考虑风速的DFIG 调频控制系统小信号模型
根据前文对不同运行风速下DFIG可参与调频动能的分析,本文将运行风速对调频动态过程小信号分析确定在中风速区。
对式(1)和式(3)的风力机功率模型和轴系系统模型线性化可得
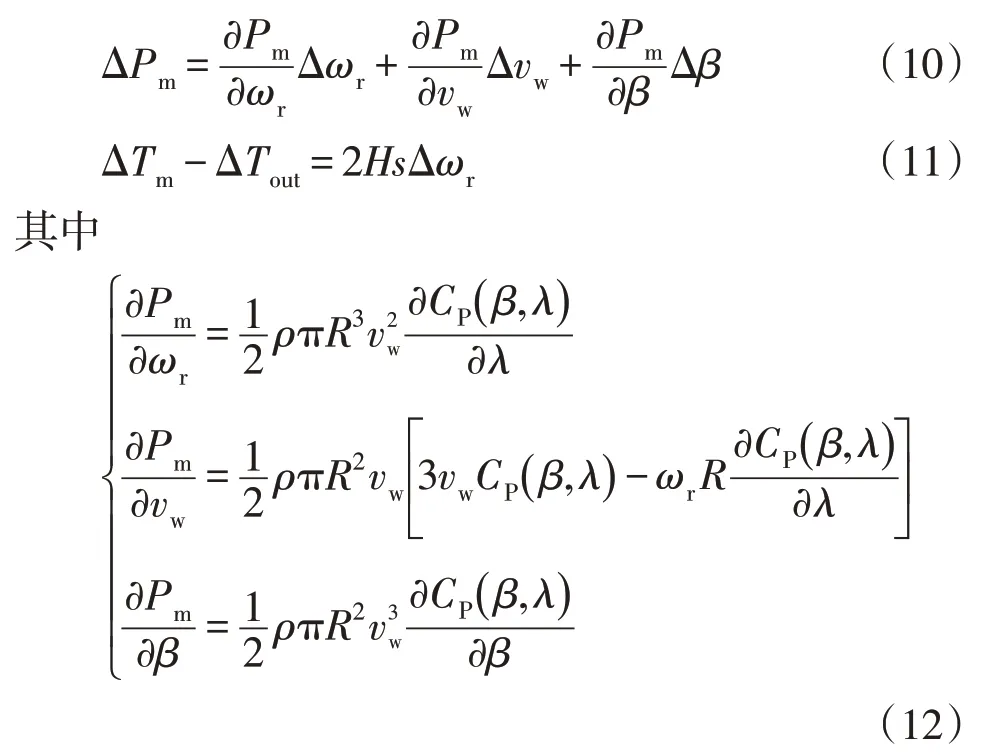
式中:ΔPm为小扰动期间输入机械功率变化量;Δωr为风机转速变化量;Δvw为风速变化量;Δβ为桨距角变化量;ΔTm、ΔTout分别为机械、电磁转矩变化量。
根据功率、转速与转矩的关系可得到

式中,Pm0、Pout0分别为初始稳定运行点的输入机械功率和输出电磁功率。
假设初始运行点系统处于平衡状态,Pm0=Pout0,联立式(2)、式(10)、式(11)、式(13)可得
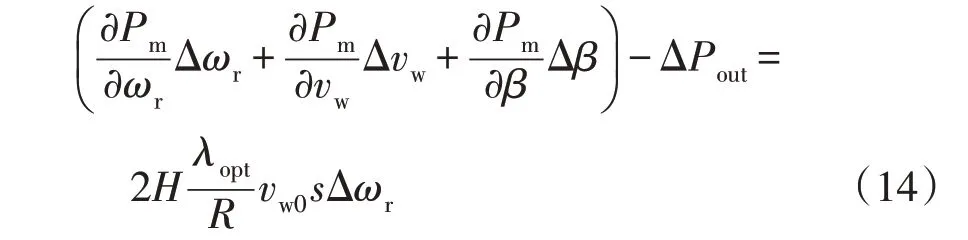
对下垂控制方程(式(4))和VSG 控制方程(式(7))线性化得到其小信号模型,即
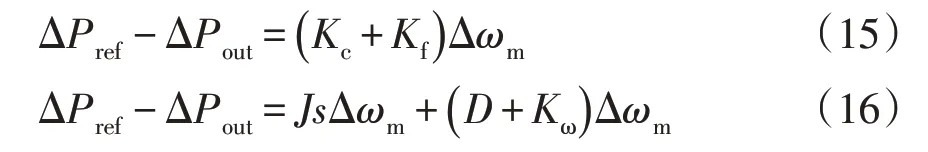
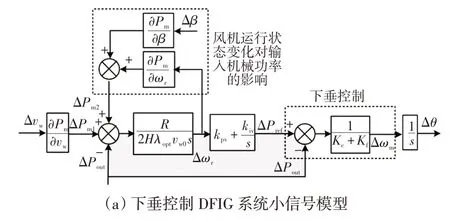
根据轴系系统模型、转速控制模型结合下垂控制/VSG 控制模型分别得到DFIG 下垂和VSG 调频控制系统小信号模型,如图4所示。

图4 DFIG 调频控制系统小信号模型Fig.4 Small-signal models of frequency modulation control system for DFIG
3 风速对VSG 和下垂控制调频性能影响对比
3.1 运行风速对VSG 控制惯性响应性能的影响
下垂控制由于缺乏惯性,对系统频率支撑能力不足。VSG控制引入了惯量和阻尼,使风机能够自发地提供惯性响应,其中引入阻尼可以减小系统频率偏差,而适当提高虚拟惯量可以减小频率变化率,提高系统频率稳定性。但DFIG 在不同工作点转子转速具有差异性,机组自身运动特性会影响系统频率惯性响应的动态过程。
假设扰动前风机运行在最佳工作点,忽略系统扰动时桨距角变化对输入机械功率的影响,此时系统处于平衡状态[26],即

式中:x0为初始稳定运行点,x0=[ωr0,vw0,β0]T;β0为风机初始运行点桨距角。
将VSG控制DFIG小信号模型进一步整理合并得到图5 所示的小信号方程。由图5 可知,双馈风机虚拟同步机(DFIG-VSG)控制系统的等效惯量Meq和等效阻尼Deq分别为

图5 DFIG-VSG 控制小信号方程Fig.5 Small-signal equation of DFIG-VSG control

式中,kpv、kiv分别为转速控制器比例和积分系数。
根据式(18)得到不同初始运行风速下VSG 控制风机系统等效惯量伯德图,如图6(a)所示。为便于分析研究,将图6(a)中所圈出部分进行放大,得到图6(b)所示的局部放大图。其中,控制参数设置为kpv=6、kiv=0.3、J=2.0。

图6 风速对虚拟同步控制DFIG 惯量特性影响Fig.6 Influence of wind speed on inertia characteristic of DFIG-VSG control
由图6 可见,风速对系统惯量特性的影响主要表现在低频和中频段,在低频段主要影响幅值特性,随着风速增大,幅值特性曲线上移,即系统的等效惯量增大;在中频段随风速增大,相位角减小。由此表明,对MPPT区而言,初始稳定运行点的风速会影响系统的惯性响应性能,风速越高,系统的惯性响应性能越强;在高频段,风速对系统等效惯量的影响不明显。
3.2 运行风速对调频控制系统稳定性的影响
根据图7所示的DFIG并网拓扑结构,可以得到DFIG调频系统输出电磁功率为

图7 DFIG 并网拓扑结构Fig.7 DFIG grid-connected topology

式中:E为DFIG 输出电压;U为电网电压;Z为系统阻抗;θ为阻抗角。
其中

式中,R、L分别为系统等效电阻和电感。
将式(20)线性化可得

假设扰动期间风速不变,即Δvw=0,根据图4可得到ΔPm1=0。由小信号模型可知,有功功率参考值的变化量为

将式(22)和式(23)代入式(16),整理可得

由于式(24)中Δωm=sΔθ,进一步化简可以得到关于状态变量Δθ的DFIG-VSG 控制系统小信号方程,即

为分析风速对VSG控制动态性能的影响,本文求取风速为7~13 m/s范围内对应的系统特征值,根据特征值的分布状况分析系统性能,结果如图8所示。
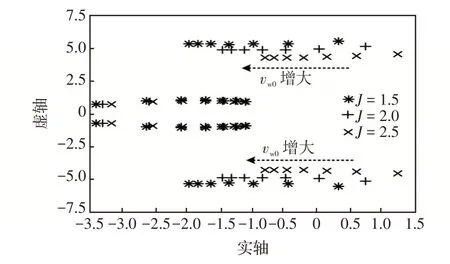
图8 不同风速下VSG 控制系统特征根轨迹Fig.8 Characteristic root locus of VSG control system under different wind speeds
根据系统特征根轨迹可知,采用VSG 控制的DFIG系统的稳定性受运行点风速影响。该系统特征值以共轭对方式出现,即

特征值的实部σ刻画了系统对振荡的阻尼,而虚部ω则指出了振荡的角频率。负实部表示衰减振荡,正实部表示发散振荡。振荡频率为

特征值s3,4的实部恒为负值,对应衰减振荡模式。随着风速增大,特征值s1,2不断左移,其实部逐步由正变负,振荡模式改变,由发散振荡变为衰减振荡,对系统稳定性起主要影响。
当特征根位于虚轴上时,系统主作用共轭特征根可表示为
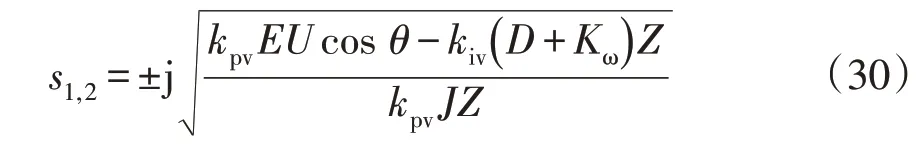
该组特征根对应的风速为

阻尼比刻画了振荡的衰减特性,阻尼比为0 表示系统处于临界稳定状态。当vw0=vov时,ζ=0,所以vov可看作VSG控制的临界风速。在控制参数固定的前提下,当vw0≤vov时,系统的一组共轭特征值位于s右半平面,DFIG系统输出功率振荡,会有失稳风险;随着风速的升高,系统特征值逐渐向s左半平面移动,当vw0>vov时,采用VSG控制系统的特征值全部位于s左半平面,振荡衰减,系统可以保持稳定。
风速对下垂控制影响分析与VSG 控制分析类似,将式(22)和式(23)代入式(15)整理可得

整理得到下垂控制小信号方程为

根据系统小信号模型得到风速为7~13 m/s 下垂控制系统特征根轨迹如图9所示。
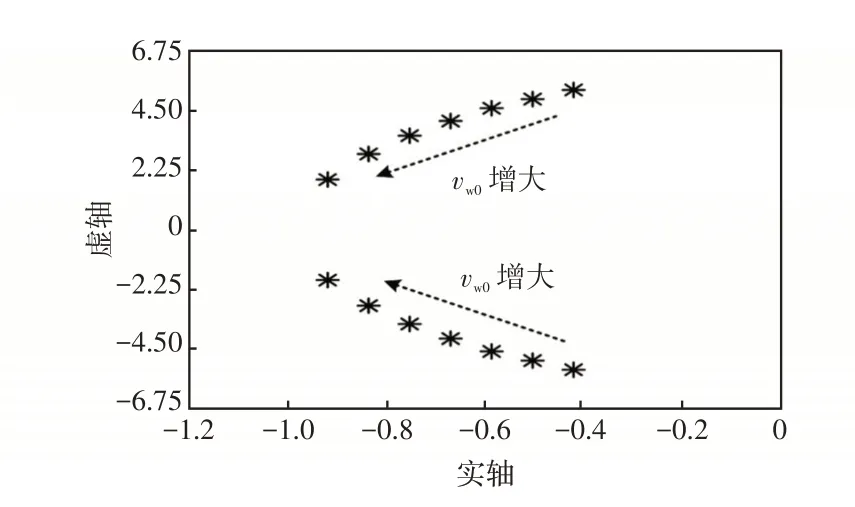
图9 不同风速下垂控制系统特征根轨迹Fig.9 Characteristic root locus of droop control system under different wind speeds
由图9 可知,在设定的风速范围内,下垂控制系统的特征值一直位于s左半平面,随着风速的增大,系统特征根轨迹逐渐远离虚轴,系统稳定性增强。
通过比较VSG 控制和下垂控制的系统特征根轨迹可以看出,惯性环节的引入使得VSG控制更容易出现输出功率振荡,特别是在较低风速时,系统有失稳的风险,此时下垂控制稳定性更好。
4 仿真算例分析
为了验证运行状态对VSG 和下垂控制调频特性影响的理论分析的正确性,基于DIgSILENT 仿真平台搭建了如图10 所示的风电并网仿真系统。该系统含两座额定功率分别为1 500 MW、300 MW 的火电厂G1和G2;在母线B4处由升压变压器T3和阻抗Z3相连,接入总装机容量为800 MW 的风电场,该风电场由额定容量为400×2 MW 的DFIG 机组等值构成,系统中风电渗透率约为30%。负荷L1、L2、L3分别为500 MW、700 MW、500 MW。仿真系统的具体参数详见附录A。仿真事件设定为风电并网仿真系统在t=90 s时负荷L1突增200 MW,在t=120 s时负荷L1突减200 MW。
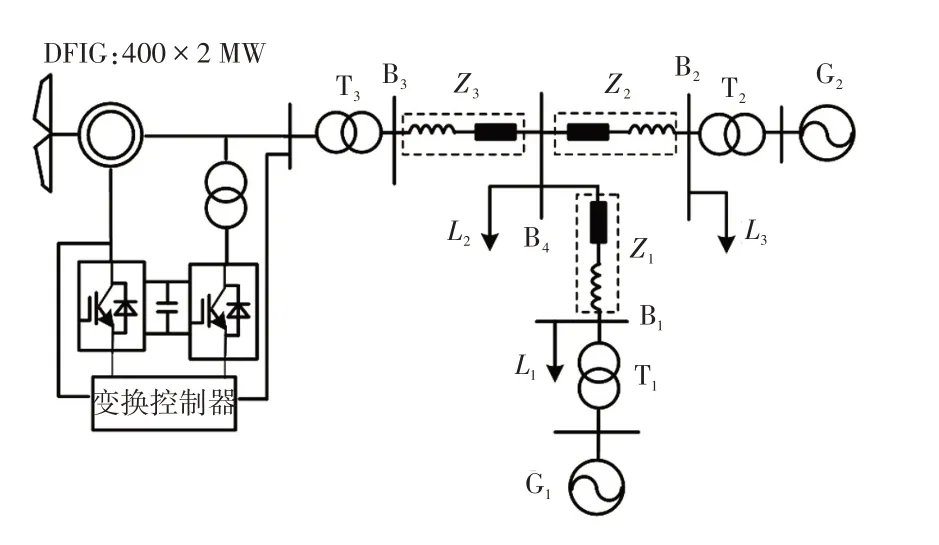
图10 仿真系统示意Fig.10 Schematic of simulation system
4.1 风速对VSG 控制系统惯性响应特性影响分析
为验证运行风速对VSG 控制风机系统惯性响应特性的影响,按照上述事件仿真,其中风速vw0分别设定为9 m/s、10 m/s、11 m/s。
图11为不同初始运行风速下采用VSG 控制的DFIG 系统突增负荷和突甩负荷时的频率变化情况。由系统频率响应可知,风速由9 m/s增加至11 m/s的过程中,系统突增负荷下频率最低值由49.705 Hz减小至49.876 Hz,频率的跌落幅度减小了58%,频率的降低速率明显减缓,频率跌落时间增加了2.57 s;在t=120 s时负荷L1突减,系统最大频率偏差减小了0.157 Hz,频率上升时间增加了2.76 s。通过对仿真结果分析可知,随着风速的增大,系统最大频率偏差和频率变化率均减小,频率响应特性得到明显改善,系统的惯性响应性能增强。

图11 不同风速下VSG 控制风机系统调频效果Fig.11 Frequency modulation effect of fan-VSG control system under different wind speeds
4.2 风速对调频控制系统阻尼特性影响分析
表2 和表3 分别给出了VSG 控制和下垂控制DFIG 系统在不同风速下的主导特征值、振荡频率和阻尼比。
由表2 和表3 的仿真结果可知,风速为8 m/s时,VSG控制系统特征值实部为正,阻尼比为负;而下垂控制系统阻尼比为正,系统更稳定。随着风速的增加,系统的阻尼比逐渐增大,振荡频率降低。在风速分别为9 m/s、10 m/s、11 m/s 时,两种控制系统阻尼比均为正,系统运行稳定,而VSG 控制系统阻尼比增长更快。在风速分别为10 m/s、11 m/s下,VSG 控制阻尼比大于下垂控制,即在一定范围内风速增大,更有利于DFIG-VSG 小干扰稳定性的提升。

表2 不同风速VSG 控制风机系统阻尼特性Tab.2 Damping characteristics of fan-VSG control system under different wind speeds
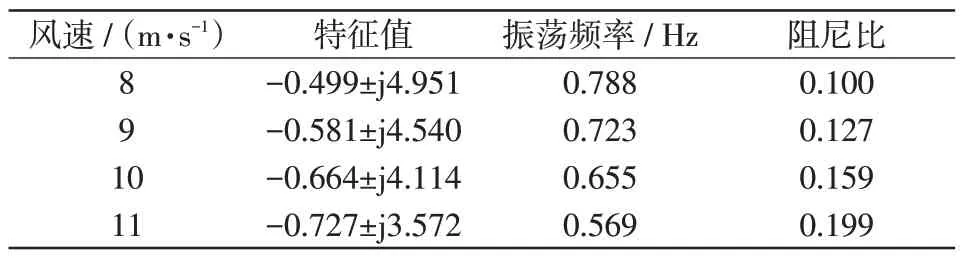
表3 不同风速下垂控制风机系统阻尼特性Tab.3 Damping characteristics of fan-droop control system under different wind speeds
4.3 不同风速下调频控制策略对比仿真分析
当系统控制参数设置如附录A所示时,计算得到DFIG-VSG临界风速vov为8.4 m/s,分别对低于临界风速(vw0=8 m/s)和高于临界风速(vw0=10 m/s)下的风机系统进行仿真分析。
4.3.1 低于临界风速调频对比
将风速设定为vw0=8 m/s,图12 给出了该风速下风电机组采用VSG控制、下垂控制及无附加控制时系统频率、风机输出功率和转速的变化对比。
频率跌落至最低点或升高至最大值的时间及最大频率偏差是直观反映风电调频效果的两项指标。风速为8 m/s 下,由图12(a)可以看出,风机系统无附加控制时,风电场对系统频率变化几乎没有响应;采用下垂和VSG 控制时,系统的频率偏差在负荷突增2.13 s 后达到最大值0.312 Hz,在负荷突甩2.91 s 后达到最大值0.307 Hz,频率最大偏差和变化率接近,但采用VSG控制频率会持续振荡。

图12 风速为8 m/s 下系统频率、风机功率与转速对比Fig.12 Comparison of system frequency,fan power and rotating speed under wind speed of 8 m/s
采用附加控制后,由风电机组的输出功率和转速响应可以看出,负荷突增200 MW后,转子转速降低,其下降幅度约为0.07 p.u.,释放出机组储存的动能,风机功率增加约为0.12 p.u.,快速补偿了系统的功率缺额,实现了对系统的频率支持;负荷突减时,风机功率减小约为0.11 p.u.,而基于机组的风电场风力机转速上升约为0.08 p.u.,风电机组通过储存动能有效削减了系统的频率增量。
图13 对比了采用不同控制策略时系统中同步发电机组G1、G2的功率响应。在风电机组无附加控制时,负荷突变导致G1的有功输出迅速变化,同步发电机的功率不平衡导致系统频率改变;当风电机组采用下垂和VSG控制时,由于风电场对系统快速的有功支持,在频率变化初期,G1的功率不平衡情况得到明显缓解,从而降低了频率的变化量。G2的有功输出恒定,不承担系统调频任务,从图13(b)可看出,当DFIG机组参与系统频率调整后,其功率能够更快地恢复稳定。与下垂控制相比,VSG控制时风机与同步机输出功率有明显波动。风速为8 m/s下,VSG 与下垂控制频率调整效果相似,但VSG 控制输出功率持续振荡,有失稳的风险。

图13 风速为8 m/s 下G1、G2 功率响应对比Fig.13 Comparison of active power response of G1 and G2 under wind speed of 8 m/s
4.3.2 高于临界风速调频对比
将风速设定为vw0=10 m/s,该风速下DFIG 系统的调频仿真结果如图14和图15所示。

图15 风速为10 m/s 时G1、G2 功率响应对比Fig.15 Comparison of active power response of G1 and G2 under wind speed of 10 m/s
图14(a)为风速为10 m/s 下DFIG 系统突增和突甩负荷时的频率变化曲线。结合表4 给出的不同控制方式下的系统最大频率偏差和频率跌落或上升时间分析可知,风速为10 m/s 时,与下垂控制相比,风电机组采用VSG 控制,系统最大频率偏差明显减小,并且VSG 控制可以降低频率变化率,频率跌落或上升时间大幅度增加,提高了系统的惯性响应能力。

表4 风速为10 m/s 下系统不同控制方式调频结果Tab.4 Frequency modulation results of system under wind speed of 10 m/s in different control modes
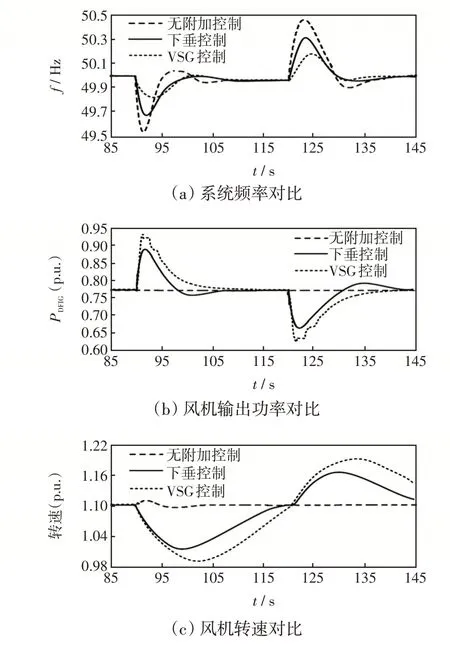
图14 风速为10 m/s 下系统频率及风机功率与转速对比Fig.14 Comparison of system frequency,fan power and rotating speed under wind speed of 10 m/s
在风速为10 m/s 下,采用下垂控制时,负荷突增200 MW 后,风机功率增加约为0.12 p.u.,转子转速下降幅度约为0.09 p.u.,从而释放机组动能,为系统提高功率支撑;负荷突减时,风机功率减小约为0.10 p.u.,转速上升约为0.08 p.u.。采用VSG 控制时,突增负荷后,风机功率增加约为0.17 p.u.,转子转速下降幅度约为0.11 p.u.;负荷突减后,风机功率减小约为0.14 p.u.,转速上升约为0.09 p.u.。在风速为10 m/s 下,与下垂控制相比,采用VSG 控制可使风电场为系统提供更多的有功支持,分担了系统突变的功率,使同步机G2的功率不平衡情况得到明显缓解,从而降低了频率的变化率及变化幅值。
综上,根据风机实际风速vw0与临界风速vov的比较结果,合理选择调频控制方式有利于在保证系统稳定的前提下,充分发挥系统的调频能力。
5 结论
本文对运行风速对VSG和下垂控制下DFIG系统调频动态性能的影响进行对比分析,推导出VSG控制临界风速的计算公式,通过理论分析和仿真对比得到以下结论:
(1)风机运行风速会影响VSG控制系统的惯性响应特性,随着风速的升高,系统的等效惯量增大,惯性响应性能增强,调频能力提高;
(2)运行风速会影响DFIG调频系统的稳定性,低于临界风速时,VSG 控制阻尼比为负,系统振荡失稳;随着风速的升高,系统阻尼比增大,振荡频率降低,相比于下垂控制而言,升高风速对VSG 控制系统的稳定性提升效果更明显。
本文针对风机运行风速对VSG 和下垂控制DFIG 系统调频能力和输出功率稳定性的对比研究,可为实际应用中适应多变的运行状态合理选择调频控制方式提供了参考。
附录A
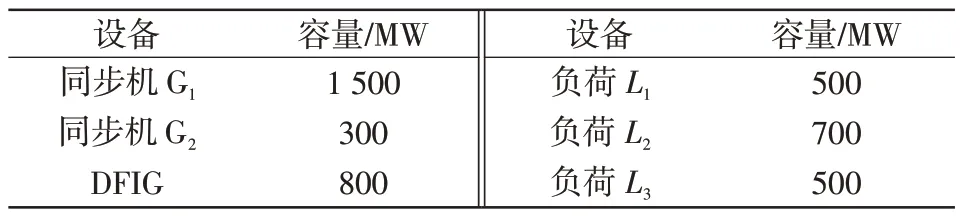
附表A-1 系统装机及负荷参数Tab.A-1 System installation and load parameters
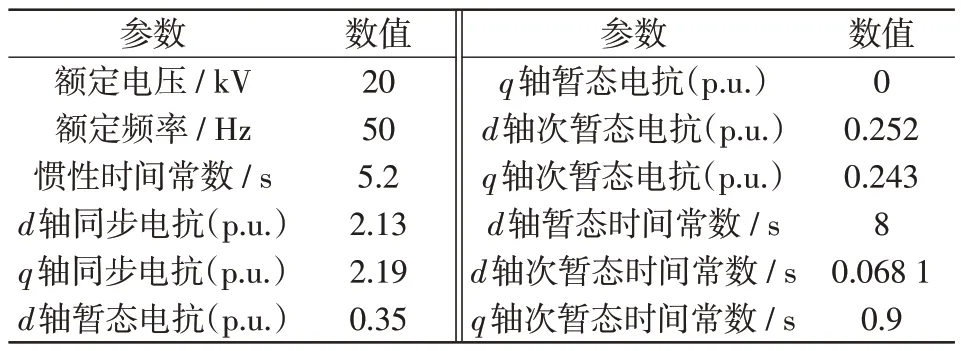
附表A-2 同步机G1 参数Tab.A-2 Parameters of G1
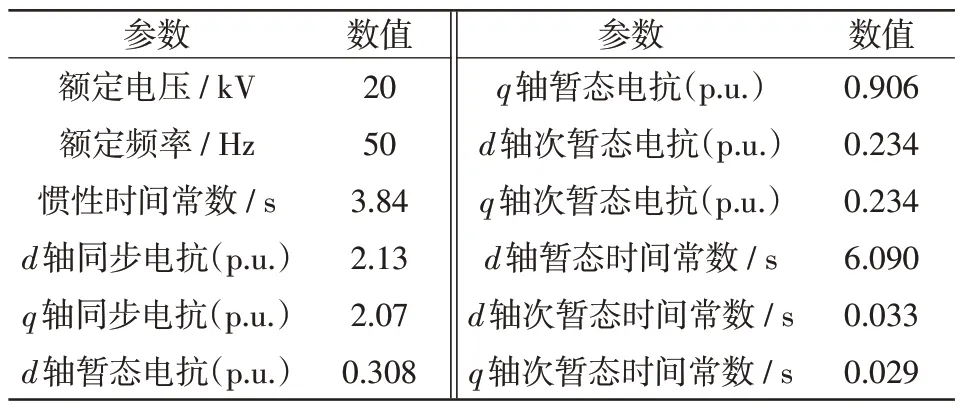
附表A-3 同步机G2 参数Tab.A-3 Parameters of G2
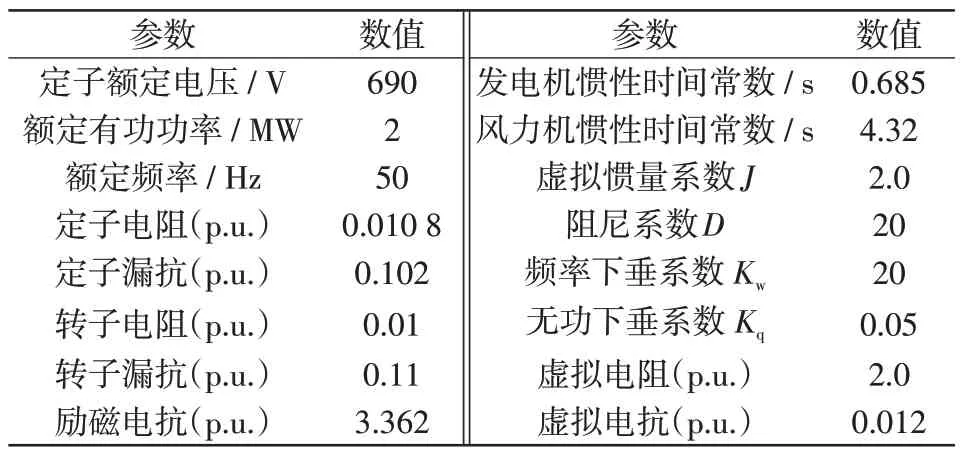
附表A-4 DFIG 参数Tab.A-4 Parameters of DFIG
