基于有效惯量分布的电力系统惯量不足概率评估
2022-08-09孙伟卿尹向阳秦艳辉
孙伟卿,尹向阳,秦艳辉
(1. 上海理工大学电气工程系,上海 200093;2. 国网新疆电力有限公司电力科学研究院,新疆乌鲁木齐 830002)
0 引言
在当前环境污染和气候变化的大环境下,世界各国都在加快能源转型。电力系统处于能源转型的中心环节,正逐步向着高比例可再生能源接入和高度电力电子化(简称“双高”特征)的趋势发展,以电力电子为接口的可再生能源成为构建新一代低碳清洁电力系统的重要举措[1⁃2]。
伴随我国碳达峰、碳中和目标的提出,以新能源为主体的新型电力系统应运而生,“双高”特征愈发显著。在此背景下,新能源比例的持续提升使得电力系统以火电厂同步发电机为主的运行方式发生改变,以变流器为代表的电力电子设备的规模化应用大幅削弱了原有系统的机械惯量,系统抗干扰能力下降,惯量不足风险加大,频率特性恶化,安全事故多发。
近年来,世界范围内发生了多起大停电事件,以澳大利亚“9·28”、英国“8·9”、美国德州“2·15”为代表的大停电事件暴露了低惯量电力系统的惯量安全问题[3⁃5],引发国内外学者的广泛关注。如何动态、定量评估系统惯量水平成为系统惯量分析问题的首要任务,也是掌握系统抗扰动能力的重要前提。因此,科学的惯量评估方法对于防范频率安全风险和维持系统稳定运行具有重要意义。
针对电力系统惯量评估问题,文献[6]介绍了含风电虚拟惯性响应的电力系统等效惯性时间常数计算方法,并分析了风电渗透率与惯性时间常数稳态值之间的关系。文献[7]提出了节点惯量的概念,针对小扰动情况,采用经验模态分解滤波器的方法提取各节点频率在频域上的幅值差异,获取系统不同时间断面各节点的惯性指标。文献[8]给出一种临界惯性计算方法,即在某发电机发生临界故障后,求取满足系统暂态稳定的惯性常数的最小值,属于满足频率变化率约束的惯性常数求解问题。文献[9]提出了惯量安全域的概念,通过建立的评估模型可确定系统惯量的安全域值和储备情况。文献[10]利用赤池信息准则确定系统辨识模型阶次,通过辨识模型阶跃响应计算惯量,减小了在线评估的误差。文献[11]则是对爱尔兰、澳大利亚和北美3 个地区电网的惯量需求进行了评估方法上的详细对比。上述评估方法涉及惯量研究的对象、区域、阈值、需求等多个方面,但并未着重考虑惯量源的状态,且提出的评估指标都是确定性指标,在概率化评估指标方面鲜有研究,忽略了故障发生的不确定性这一影响系统惯量安全评估的重要因素。发电机组作为系统惯量的主要提供者,其运行状态对于保障系统惯量水平至关重要。在英国“8·9”大停电事件中,除了系统惯量水平偏低外,火电机组意外停运成为大停电事故的主要诱因之一,这表明现实中机组的非计划停运无法避免,惯量源的强迫停运不可忽视。因此,需要将发电侧故障发生的不确定性纳入系统惯量评估环节,给出能够刻画潜在故障下电力系统惯量不足风险程度的概率指标。
本文提出一种基于有效惯量分布的电力系统动态安全评估方法。首先,在现有惯量分析技术的基础上,通过求解机组组合确定各惯量源的运行状态,通过计算稳态和扰动下的惯性常数确定系统的惯量评估参考值。然后,考虑机组的强迫停运率建立有效惯量概率模型,通过半不变量法和Gram-Charlier级数展开进行有效惯量分布的构建,获取连续的有效惯量概率分布曲线,进而依据曲线定义惯量不足概率指标对系统惯量安全进行评估。最后,在改进的IEEE 39 节点测试系统中进行评估验证,并给出了稳态和扰动下的惯量安全评估结果。
1 电力系统惯量定义与分类
1.1 惯量定义
惯性作为能量的一种属性,在力学中表现为物体对于运动状态变化的抵抗能力[12]。对电力系统而言,惯性表现为系统对功率波动的阻抗能力,由于有功功率与频率密切相关,故电力系统惯性也可以理解为系统阻碍频率变化的能力。
描述惯性大小的量值称为惯量,物体的惯性大小即为质量,电力系统的惯性大小则可以用惯性常数H进行度量。电力系统的频率稳定与有功平衡情况和系统惯量有关,且满足式(1)所示的摇摆方程。

式中:Hsys为系统惯性常数;f为系统频率;D为阻尼系数;Δf为系统频率偏差;Pm为机械功率;Pe为电磁功率。
当系统出现不平衡功率时,同步发电机中储存的动能将以惯量支撑功率的形式进行惯量响应,减缓频率下跌速率,并为一次调频赢取时间。因此,系统惯量水平对于应对故障扰动和维持频率稳定至关重要。
1.2 惯量分类
1.2.1 传统惯量
电力系统中的传统惯量以同步发电机为主导,相较于负荷侧的异步电动机,同步发电机的可控性更强,其表现出的阻尼特性和惯性对系统的稳定运行具有重要作用。对于同步发电机而言,常见的惯量表示有转动惯量J、惯性常数H和惯性时间常数Tj3种。其中,J表示机械质点与转动半径的关系特征,其值为一常数;H表示机组仅用存储动能进行额定发电所持续的时间;Tj表示转子施加额定转矩后,机组由静止到额定转速所需要的时间。J、H、Tj的具体计算公式分别如式(2)—(4)所示。
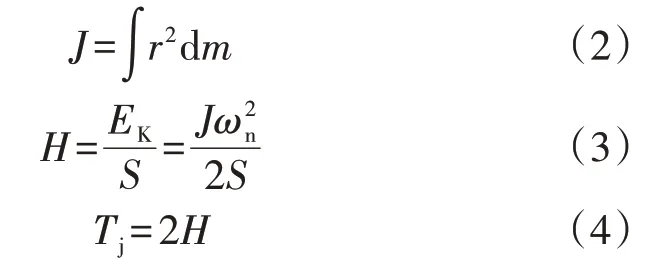
式中:r为转子半径;m为刚体质量;EK为额定转速下的转子动能;S为额定容量;ωn为额定机械转速。
需要注意的是,同步发电机组所表现出的惯量特性仅与机组额定转速下的动能和额定容量有关,而与当前运行的有功出力无关。
1.2.2 虚拟惯量
近年来,得益于虚拟同步发电机VSG(Virtual Synchronous Generator)等技术的发展[13⁃16],电力系统中如风轮、储能等设备中存储的其他形式的能量也可以通过合理的控制策略提供惯量支撑,从而参与系统的频率响应过程。这类资源提供的等效惯量称为虚拟惯量,相应的控制方法称为虚拟惯量控制方法。
VSG 按照控制方式和外特性可分为电流源型和电压源型两大类。电压型VSG 技术相较于电流型具有电压和频率支撑的能力,拥有更为广阔的应用前景。但无论是电流型还是电压型VSG 技术,其所需要模拟的惯量支撑功率P(t)的表达式均为[17]:

式中:f0为系统额定频率;PN为同步机的额定功率。
现阶段电力系统中所需要的惯量主要仍由传统惯量负责,火力同步发电机组目前既是主要的能源供应者,又是系统惯量的有效提供者。而伴随着可再生能源的迅速发展,新能源在配备VSG 技术后也能为系统带来显著的惯量支撑效果,具有巨大的发展潜力和应用空间,虚拟惯量将会成为惯量调节不可或缺的重要手段。
2 电力系统惯量安全评估
2.1 惯量源参与状态的确定
评估周期内惯量源参与状态的确定,是开展系统惯量安全动态评估的前提条件,即需要通过各个时刻的机组开机和运行状态判断当前机组是否可以为系统提供惯量支撑。因此,通过机组组合确定评估时段内各台机组的运行状态,该问题的目标函数为:

式中:x为布尔变量,表示机组启停状态;y为连续变量,表示机组发电功率、线路传输功率、负荷等;c′为机组启停成本和固定成本系数;b′为机组发电成本系数。
约束条件分为以下3类:
1)离散变量约束,包括机组最小启停时间、启停逻辑约束等;
2)连续变量约束,包括功率实时平衡约束、旋转备用约束、线路潮流约束等;
3)离散变量和连续变量耦合约束,包括机组发电容量约束、可再生能源出力范围约束、机组爬坡约束等。
关于机组组合模型的具体形式,此处不再赘述。
2.2 电力系统惯量评估值的确定
“双高”电力系统的惯量是时变的,及时准确地获取系统惯量水平能够指导发电和调度计划,避免惯量事故的发生。不同惯量水平下的评估结果是不同的,下面从稳态和扰动两方面选取合适的惯性常数作为评估参考值。
依据惯量守恒定律,电力系统整体的惯量水平可由系统包含的多种惯量源确定,系统稳态时,系统的等值惯性常数可由式(7)确定。

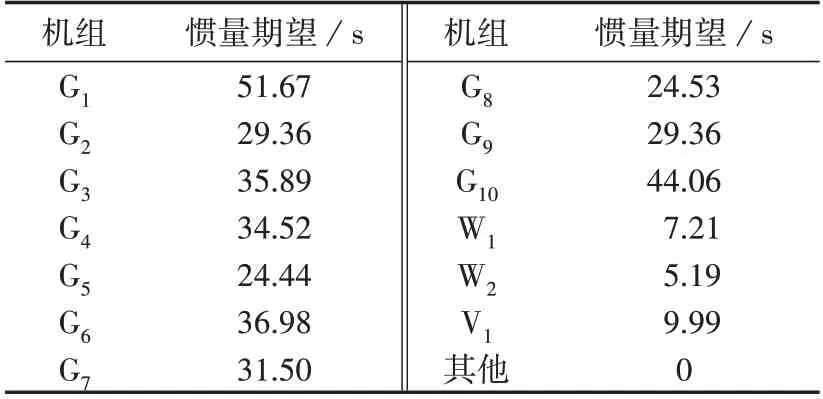
当借助惯性常数判别系统惯量安全时一般遵循如下标准[20]:如果Hsys>4 s,则系统惯量充足;如果3 s 当系统发生扰动时,可根据不平衡功率的大小与系统频率变化率限值fRoCoFmax求取系统惯性常数,澳大利亚能源市场运营商AEMO 将其定义为安全运行惯量SOLoI(Secure Operating Level of Inertia)HSOLoI,定义式如下[21]: 式中:ΔP为扰动造成的不平衡功率;Eloss,max为可能出现的最大惯性机组动能损失。 SOLoI 值的大小会随着不平衡功率的变化发生改变,计及了惯性最大机组的动能损失,能够获取系统发生故障时的惯量安全阈值,适合作为扰动时的惯量评估参考值。 式中:HG,i为机组i的惯性常数,对于新能源机组而言,若其配备有VSG 技术,则HG,i的值为所能提供的虚拟惯量,否则HG,i=0;pFOR,i为机组i的强迫停运率。 惯量源机组有效惯量的矩可由式(10)求得。 式中:ai,v为机组i的有效容量v阶矩。在已知矩信息后,可由不高于相应阶次的矩求取半不变量。半不变量也叫累积量,其数字特征可在一定程度上反映分布特性。通过矩和累积量之间的数学关系,可求得机组i的各阶累积量如下: 式中:κi,v为机组i的有效容量v阶累积量。 为了确保系统惯量安全,按照惯性常数从大到小的顺序对机组进行排序,从而确定机组的加载顺序。前k台机组依次加载后的系统有效惯量分布可由已加载机组有效惯量分布卷积得到,即: 式中:“*”表示卷积运算。 由于半不变量具有可加性,即独立随机变量和的累积量等于其各自累积量之和,因此独立随机变量的卷积运算可以简化为半不变量的求和运算。前k个机组等值有效容量的半不变量为: 式中:Kk,v为前k台机组等值有效容量v阶累积。 在计算得到各阶半不变量后,可采用Gram-Charlier 级数展开的方法,将随机变量的概率分布函数展开为由正态随机变量的各阶导数所组成的级数,上述求得的各阶半不变量即为展开级数的系数,以此逼近得到累积分布函数。为了简化级数的形式,定义:式中:Kv为v阶半不变量;gv为v阶规格化半不变量;σ为标准差。 进一步地,为了简化级数计算,将随机变量也进行规格化,其形式为: 式中:ϕ(⋅)为标准正态密度函数;Hv(xˉ)为Hermite多项式。 图1 给出了前k台机组加载后的有效惯量概率分布的图形表示。 图1 有效惯量概率分布Fig.1 Probabilistic distribution of available inertia 图1 中前k台机组加载后的有效容量分布Fk( ) x表示当前时刻系统惯量水平低于惯量评估值x的概率。不同时刻下的评估参考值Ht与惯量源的参与状态相对应,此时的Ht可依据2.2 节中所述的稳态时的惯量安全判据Hsys或者扰动下的HSOLoI求得,k值为机组组合求解后的惯量源参与数目。具体地,当t时刻的评估参考值为Ht时,Fk( )Ht表示系统惯量小于Ht的概率,同时也是前k台机组加载后面对Ht的惯量不足概率。由此定义系统惯量不足概率ISP(Inertia Shortage Probability)为: 需要指出的是,安全性评估中有效惯量概率分布应该由机组组合求解出的机组状态来确定当前评估时段下的Fk和Ht,任一机组状态的改变(投入或切出)都会对曲线产生影响,这也是该评估方法“动态”特性的体现。 综上所述,可得到基于有效惯量分布的动态安全评估流程如图2所示。 图2 基于有效惯量分布的动态安全评估流程Fig.2 Flowchart of dynamic security assessment method based on available inertia distribution 本文选取改进的IEEE 39 节点测试系统验证所提惯量分布模型和动态安全评估方法的有效性。该系统在原IEEE 39 节点测试系统的基础上,增设5 座风电场和3 座光伏电站,将节点4 处负荷改造为500 MW 的直流输送功率,其网络拓扑结构见附录A 图A1。其中,2 号机组为平衡机组,系统的额定频率为60 Hz。算例所使用的机组数据见附录A 表A1、A2。 由于实际电力生产中惯量源所提供的动能难以衡量,而系统当前的机组容量容易获取,为此利用标幺制的思想引入基准值Sbase=100 MW 来完成不同时段下惯量需求的转化而不必考虑动能变化,具体公式如下: 式中:H′为基准值Sbase下的惯性常数。 选取惯量评估周期为24 h,通过MATLAB 求解考虑安全约束的机组组合问题,得到评估时段内火电、风电和光伏机组的出力情况见附录A图A2。 在机组运行状态确定后,为了探究新能源与VSG 技术对电力系统惯量的影响情况,构建以下4个系统运行场景,用以评估系统惯量特性。 1)场景1:新能源电站正常接入系统,各新能源电站均不具备惯量支撑能力。 2)场景2:风电场机组W1、W2具备VSG 技术,能够提供虚拟惯量。 3)场景3:光伏电站机组V1具备VSG 技术,能够提供虚拟惯量。 4)场景4:风电场机组W1、W2和光伏电站机组V1具备VSG技术,能够提供虚拟惯量。 场景1—4 模拟的是电力系统当前阶段和施加提升措施后的惯量状况,场景1 的惯性时间常数为3.73 s,按照3 s 图3 依次加载的有效惯量概率分布Fig.3 Probabilistic distribution of available inertia after sequential loading 通过构建有效惯量概率分布可以对评估周期内的惯量安全性进行评估,各时刻的评估结果如图4所示。图中,确定性指标惯性常数的评估结果均处于[3,4]s 范围内,说明系统在评估周期内表现出的惯量水平一般,但当前系统所面临的惯量安全风险尚不明确。本文所提评估方法能够针对3 s 图4 不同场景下的惯量安全评估结果Fig.4 Results of inertial safety assessment in different scenarios 依据划分时段对图4 所示的结果进行分析,可得到下列结论。 1)对于场景1 不具备VSG 的新能源电力系统而言:00:00—05:00时段,风电场出力较大但用电需求较少,导致系统接入的火电机组数量较少,能提供给系统的惯量支撑有限,造成该时段的惯量不足概率较高;06:00—09:00 时段,光伏电站开始发电,但由于光伏本身并不具备提供惯量的能力,对于系统而言相当于以初始的动能去支撑容量更大的系统,从而造成惯量不足概率的迅速攀升,该时段也成为整个评估周期的峰值时段;10:00—13:00时段,随着用电高峰的来临,火电机组全部投入电能生产,为系统提供了有力的惯量支撑,系统的惯量不足概率也随之下落;14:00—18:00时段,火电机组数量随着负荷下降而减少,惯量不足风险回升;18:00—21:00 时段,随着光伏的退出以及用电晚高峰的来临,火电机组开始承担电力供应的主要任务,系统惯量情况出现好转,安全风险快速降低;22:00之后,负荷的降低和风电出力的增加使得部分火电机组关机,系统惯量不足概率有所回升。 2)对于配备有VSG 技术的场景2—4,系统表现出的惯量不足概率变化趋势与场景1 中一致,但由于虚拟惯量的作用,对应时刻下的惯量不足概率显著降低。其中,光伏电站由于光照限制并不能在夜晚改善系统惯量情况,而风电在全天均有出力可以缓解各时刻下的惯量不足压力。同时风电和光伏电站,逐步提升VSG 技术在新能源电站中的应用比例,得到的系统惯量不足概率和动能变化趋势如图5所示。 图5 VSG应用后系统惯量不足指标和动能的变化趋势Fig.5 Variation tendency of inertia deficit indicators and kinetic energy after VSG application 此处所提系统动能为广义动能,包含了虚拟惯量所提供的能量形式。随着VSG 应用比例的逐步增加,系统的动能水平得到提升,惯量不足概率随之下降,系统动能和惯量不足指标分别呈现上升和下降趋势,由此可说明VSG 确实有助于改善系统惯量情况,提升系统惯量水平。 随着电力系统“双高”特性的日益凸显,直流闭锁和新能源脱网事件对系统安全稳定造成了十分恶劣的影响,以场景4 为例,从惯量安全角度对以上两方面进行探究。当节点4 发生直流单极闭锁后,系统出现盈余功率,初始频率变化率为0.196 Hz/s,此时需要采取稳控切机措施以解决高频问题。通过计算系统所含惯量源的惯量期望EIS可以为高频切机方案的制定提供参考,其公式为: EIS受到机组自身容量、惯性常数以及强迫停运率的影响,反映了机组对于系统惯量的贡献程度,其值越大意味着所提供的惯量效果越好。 表1 给出了基准值下各台机组的惯量期望计算结果,其中新能源电站由于容量小、动能小,故所求的惯量期望不及常规机组。依照表1 结果可以优先选择惯量期望值较小的机组进行切除,以确保系统惯量不会随容量骤减。 表1 不同机组所提供的惯量期望Table 1 Expectation of inertia provided by different units 为了探究新能源脱网对系统惯量安全的影响情况,以风电机组W2脱网为例,开展扰动下的惯量安全性评估。图6 给出了评估时段内不同时刻W2以不同功率退出运行的惯量安全评估结果。图中,时刻0—23 分别表示00:00—23:00。由图可见,当不平衡功率数值较小时,系统凭借自身的惯量储备能够承担扰动影响,但随着不平衡功率的逐步扩大,系统所需的安全运行惯量逐步增加,惯量不足概率将会迅速上升,当系统的惯量供给无力承担功率损失后的惯量需求时,系统面临惯量危机,安全问题凸显。此外,从不同时刻的惯量评估结果可看出,火电机组开关机状态显著影响系统惯量水平,开机机组的安全性价值不容忽视。 图6 不同损失功率下的惯量安全评估结果Fig.6 Results of inertial safety assessment under different loss power values 当系统的惯量支撑能力不足时,系统的频率调节能力也被进一步削弱,在不平衡功率的冲击下,频率偏差逐步增大,极易导致频率失稳,触发低频减载,造成更大的安全事故。因此,在关注系统惯量水平的同时还应该聚焦于扰动后的频率变化。表2 给出了不同时段下系统惯量不足概率首次达到1 时损失功率对应的频率变化率(RoCoF)。 表2 不同损失功率下的频率变化率Table 2 Rate of frequency change under different power loss 分布式电源的频率变化率保护装置的启动阈值为±0.125 Hz/s,表2中绝大多数时刻的损失功率所对应的频率变化率超过了该阈值,将会触发保护装置动作,造成分布式电源脱网并进一步扩大损失功率,导致系统频率状况进一步恶化。因此,在考虑提升系统惯量水平的同时还应关注系统的频率调节能力,加强并完善安全稳定三道防线的保护策略,以应对功率冲击造成的频率快速跌落,降低系统在低惯量状态下的安全风险。 近年来,电力工业生产技术和管理水平日益完善,火电机组的可靠性得到了极大的提升,有效降低了安全事故的发生频率,相较之下,新能源电站具有更强的不确定性和不可控性。通过进一步降低常规机组的强迫停运率(设置为0)对系统惯量水平进行评估,发现之前06:00、07:00 时刻处于峰值的惯量不足概率下降为0.116,其余时刻的惯量不足概率均为0。由此说明,在面向可靠性较强的系统时,仅凭火电机组便可承担系统绝大多数的一般性惯量需求(3 s 传统的电力系统惯量评估方法通常会给出确定性的数值指标,对于不同评估时段下的概率性指标鲜有涉及。针对这一问题,本文采用基于有效惯量分布的概率评价方法,在考虑系统惯量源参与状态与惯量评估参考值的基础上,定义系统惯量不足概率指标,对评估周期内的系统惯量水平进行动态评估。研究得出以下结论: 1)本文所提有效惯量分布曲线反映了机组潜在故障下的惯量供需平衡关系,其期望指标可以对系统所含惯量源的重要程度予以判别,惯量不足概率指标也可以对扰动后的惯量不足程度进行刻画; 2)对于尚未出现惯量不足或惯量充足的系统,在考虑了机组强迫停运率后,评估时段内的惯量不足概率并不为0,这表明机组随机故障带来的惯量安全风险更甚于容量安全风险; 3)电力系统惯量水平受到动能、接入机组额定容量、强迫停运率等多方面的影响,通过虚拟惯量控制技术能够扩充系统动能,降低系统惯量不足概率,是“双高”电力系统必需的惯量安全提升措施; 4)伴随着惯量源的日内启停,电力系统惯量水平显示出显著的时序性差异,在未来“双高”新型电力系统中,需要关注机组投切状态对惯量安全的作用价值并做好新能源机组随机故障的风险防范。 “双高”电力系统频率稳定性问题日益突出,今后应在获取惯量评估结果的基础上着重考虑低惯量水平下的频率稳定问题,完善相应的保护措施并制定合理的应对策略。 附录见本刊网络版(http://www.epae.cn)。
2.3 有效惯量分布的累积构建







2.4 惯量安全评估指标

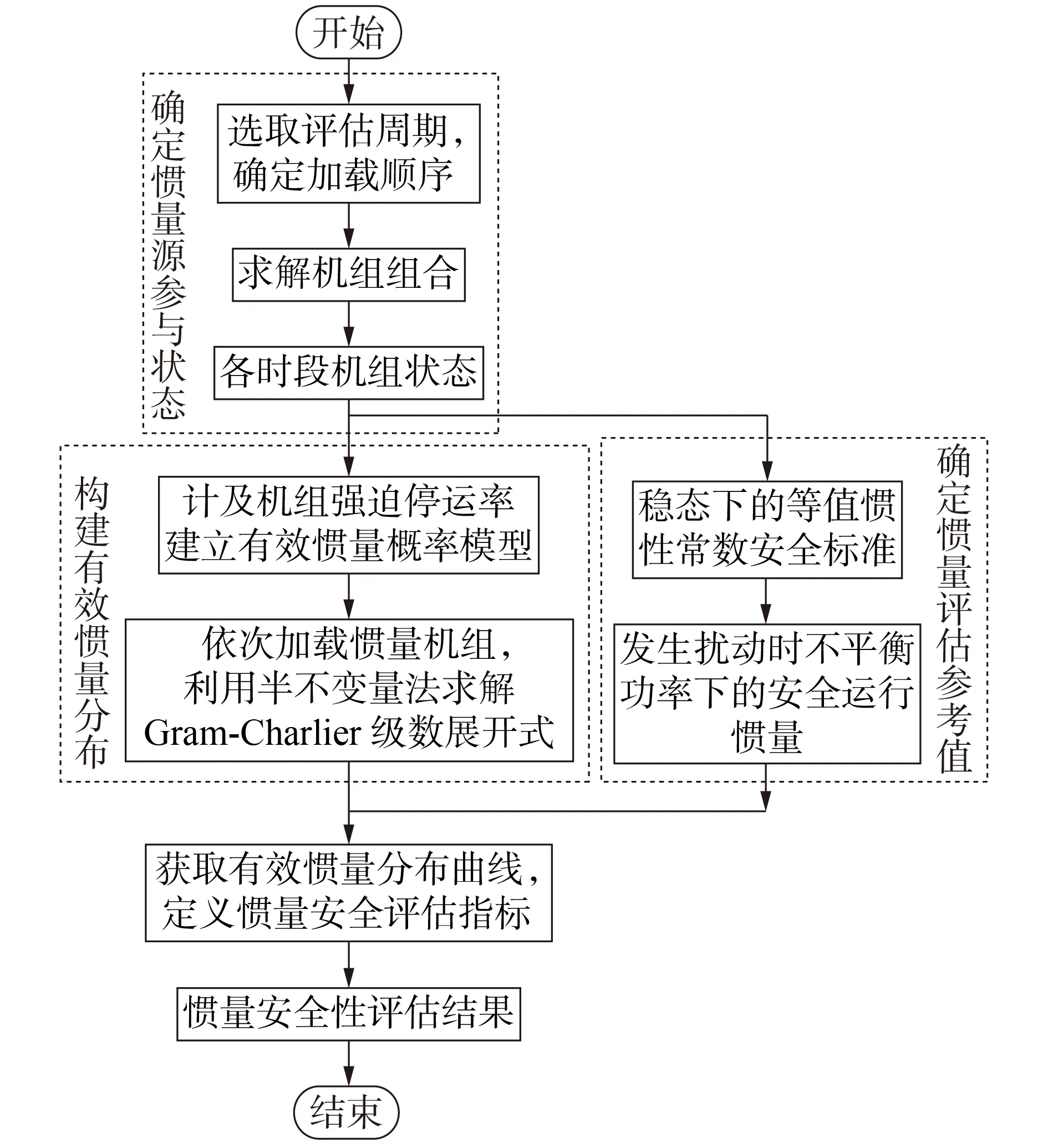
3 算例分析
3.1 系统简介与场景设置

3.2 稳态下的惯量安全评估



3.3 扰动下的惯量安全评估



4 结论
