基于STL 与MMoE 多任务学习的区域多光伏电站超短期功率联合预测方法

王本涛，白 杨，邢红涛，徐 岩

（1.国网呼伦贝尔供电公司，呼伦贝尔 021000；2.河北冀研能源科学技术研究院有限公司，石家庄 050071；3.华北电力大学电力工程系，保定 071003）

随着光伏装机容量的不断增长，电网中光伏发电接入比率不断提高。在这种背景下，为保证电网的安全稳定运行，准确的光伏功率预测不可或缺。光伏电站是典型的间歇性能源，其发电能力受外部环境影响较大，波动性强，实现精准的光伏功率预测对提高光伏电站控制调度性能意义重大[1]。光伏预测从时间尺度上可以分为超短期、短期和中长期预测，其中超短期光伏预测能够提供光伏出力的详细变化信息，反映功率瞬变的波动细节，因而相关研究获得了广泛关注。

从预测方法来看，已有研究所用的光伏功率预测模型大体可分为统计模型[2-4]、神经网络模型[5]、传统机器学习模型[6]3 类。统计模型以时间序列分析为理论基础，通过光伏功率历史数据进行建模，理论完备，可解释性好。例如文献[2]中分析了光伏出力存在周期性与随机性，通过太阳辐射模型与最小二乘理论提出了随机分量提取方法；文献[3]通过多重线性回归分析构建了光伏功率预测模型。但是，由于光伏功率与多维特征之间存在复杂的非线性关系，因而统计模型的光伏功率预测精度不够理想。

目前，随着深度学习等技术的发展，神经网络模型，特别是深度神经网络模型在光伏功率预测中得到了广泛应用。深度神经网络模型具有特征提取能力强、能够建模时间序列波动特性等优势。文献[7-8]通过长短时记忆网络LSTM（long short-term memory）构建了短期光伏发电预测模型；文献[9]则是采用了卷积神经网络CNN（convolutional neural network）-LSTM 作为预测模型；文献[10]基于互信息熵对已有LSTM 模型进行改进，提出了基于互信息熵MIE（mutual information entropy）-LSTM 的短期光伏功率预测方法。但是，这些方法仅适用于单个光伏电站，无法考虑多光伏电站之间的相关特征，且在高级特征有效性方面有待加强。考虑到神经网络初始权重与参数选择问题，文献[11]提出了一种双模式布谷鸟搜索算法对小波神经网络进行优化，提高了其收敛速度。文献[12-13]也采用了改进的搜索算法来优化神经网络的超参数。参数优化的目的是通过控制网络深度来确保特征有效性，但搜索过程较为复杂。近年来研究表明可以利用注意力机制实现高级特征的自动增强[14]，从而降低参数搜素过程中的计算成本，但目前该方法在光伏功率预测方面的研究还鲜见报道。

为提高模型的预测效果，已有不少研究在输入特征方面进行改进，例如对功率曲线进行分解[6-7，15-16]，或者选定影响功率的主导因素[8-9，17]。在光伏功率分解方面，变分模态分解[6]、经验模态分解[7]、小波包变换[16]都是近年来常用的方法。这些功率曲线分解算法偏重于分解信号的高频、低频分量，对光伏功率的周期性考虑不充分，可解释性较差。而在影响因素选择方面，文献[8，17]通过历史功率曲线聚类来提取光伏功率与特征之间的关系，进而确定输入特征。文献[9]则是通过Granger因果关系算法选择出关键气象因子作为输入。文献[5]通过对历史气象因素进行密度峰值聚类，利用统计指标构建天气特征向量。文献[11]中利用C-C方法进行混沌吸引子重构，挖掘各因素信息对光伏发电功率的影响。

由于目前光伏功率预测对象往往是单个光伏电站，已有研究往往是从单个电站的角度来考虑输入特征，同一区域内不同光伏电站功率的相关性特征还少有考虑。同一区域内气象环境变化具有连续性，基于不同光伏电站历史功率进行联合预测有助于提高预测精度，降低计算成本。对于区域多光伏电站的功率预测问题，传统机器学习方法或统计学方法需要对每个光伏电站分别建立单独模型进行预测。这种处理方式忽略了不同光伏电站功率预测问题中存在的潜在相关性，同时存在重复建模、计算成本高的问题。而多任务学习仅需要建立1 个模型，将不同光伏电站的功率预测视作是该模型的子任务，通过不同任务之间的信息共享提高每个子任务的预测准确性。

综上所述，本文提出了一种基于季节性分解STL（seasonal and trend decomposition using loess）与MMoE多任务学习的区域多光伏电站超短期功率联合预测方法。首先，对光伏功率曲线进行STL，从而确定光伏功率曲线的周期分量、趋势分量与剩余分量，进而通过MMoE多任务学习方法挖掘同一区域内不同光伏电站功率的剩余分量与趋势分量之间的相关性，通过注意力机制改进的深度神经网络模型进行预测。

1 预测模型构建流程

首先，将区域内不同光伏电站功率曲线进行STL，分别得到周期分量、趋势分量、剩余分量3 种曲线。对于提取得到的周期分量，可直接通过其参数进行外推，无需预测。对于趋势分量与剩余分量，将光伏电站的历史分量数据与气象因素数据共同作为输入特征进行训练，深度神经网络模型采用注意力机制进行改进，采用MMoE多任务学习方法来挖掘不同光伏电站功率之间的相关性，从而实现不同光伏电站功率未来趋势分量与剩余分量的准确预测。最后，通过对3种分量进行相加得到光伏电站功率超短期预测结果。预测模型构建如图1所示。

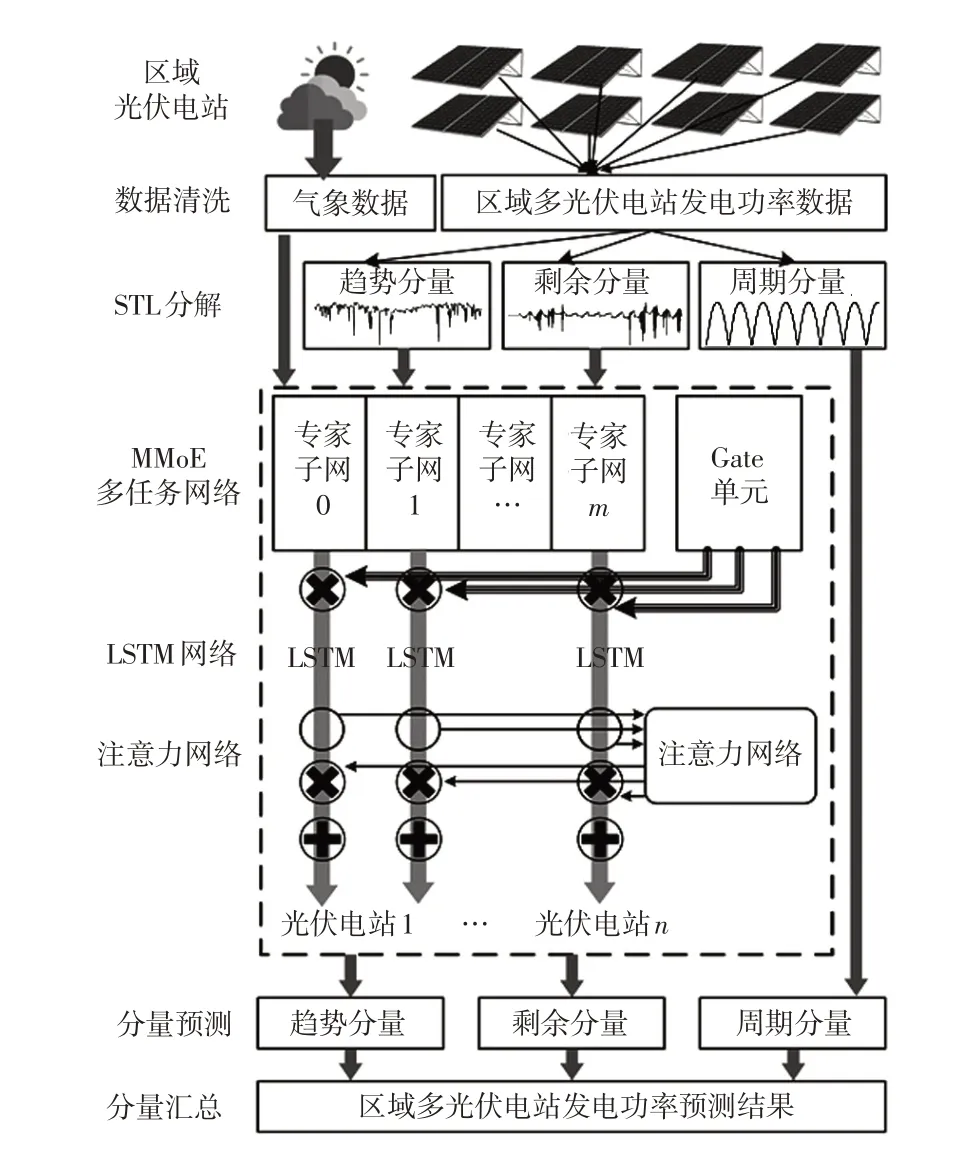
图1 预测模型构建Fig.1 Construction of prediction model

2 STL 模型

STL方法是一种基于局部加权回归散点平滑算法（loess）的时间序列分解方法，能够将时间序列分解为周期分量、趋势分量、剩余分量3部分。STL包括内循环和外循环两个部分，其中内循环主要通过去趋势、去周期、平滑滤波等步骤获得趋势分量与周期分量；外循环则是通过稳健性权重削减离群点的影响。

STL 模型可以分为加法模型和乘法模型两种。乘法模型意味着不同分量之间存在相互影响，而对于本文所述的光伏功率预测问题，不同分量之间彼此独立，因此加法模型更为适用。以某周光伏电站实际出力功率曲线为例，STL结果如图2所示。

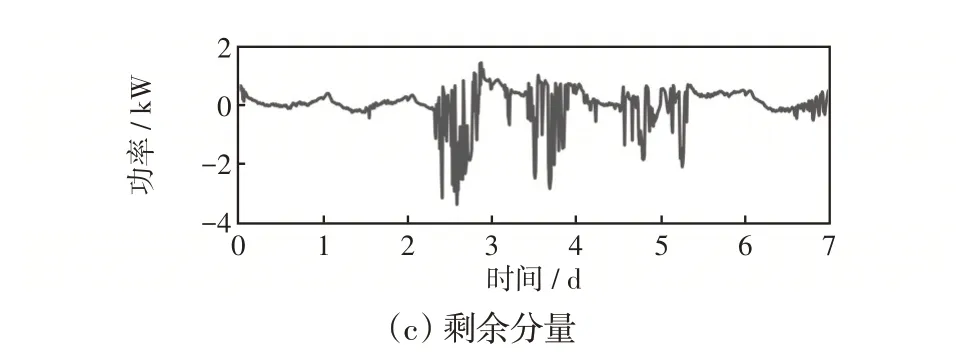
图2 光伏功率STL 典型分解结果Fig.2 PV power decomposition result based on typical STL

对于本文所述的区域多光伏电站功率预测问题，同一区域内不同光伏电站的功率具有显著一致的周期性，且趋势分量与剩余分量的变化存在密切相关性，因此分解后的结果对预测问题而言是有益的。

3 基于注意力机制与LSTM 的MMoE 多任务学习模型

3.1 多任务学习MMoE 模型

多任务学习从实现方式上可以分为硬共享机制与软共享机制，硬共享机制中通过参数共享来实现特征提取与输出，而软共享机制中每个任务都具有单独的参数。考虑到区域多光伏电站的功率相关性较为显著，并且不同子任务之间性质相近，因此本文采用硬共享机制实现多任务学习，其原理如图3所示。

图3 基于硬共享机制的多任务学习Fig.3 Multi-task learning based on hard-sharing mechanism

对于多任务学习，任务之间的关系会极大地影响多任务模型的预测质量。因此，实现特定任务目标和任务间关系之间的建模权衡是非常重要的。MMoE 模型很好地解决了这一问题，通过将共享层划分为多个专家子网（expert），利用门控（gate）机制实现了共享层的灵活组合[18]，模型如图4所示。

图4 MMoE 模型原理Fig.4 Principle of MMoE model

设输入为x，共享网络底层为f(x)，子任务独立输出层为hk(x)，其中k表示第k个任务，则第k个任务的输出yk可表示为

式中：n为任务数；gk,i(x)为第i个专家子网门控单元的输出；fi(x)为第i个专家子网的输出。

3.2 LSTM 子任务层

对于MMoE 模型，专家子网负责提取不同任务之间的相关性特征，后续子任务层可依据不同任务需求选择。对于光伏电站预测问题，此处选择LSTM单元组成子任务层。LSTM单元的结构如图5所示。

图5 LSTM 单元结构Fig.5 Structure of LSTM unit

LSTM 单元输入的相关变量包括当前输入xt、前1 个单元的输出ht-1、前1 个单元的状态ct-1、输出变量即当前单元输出ht、当前单元状态ct。LSTM单元包括遗忘门、输入门和输出门，其机制可表示为

式中：ft为遗忘门的输出，用于控制前一状态信息对当前状态的影响；it为输入门的输出；ot为输出门的状态；Wf、Wi、Wo、Wc分别为网络激活函数输入的权重矩阵；bf、bi、bo、bc为偏置项；σ（）为sigmoid函数；[]表示向量连接组合；符号∘表示Hadamard乘积运算。

3.3 注意力机制

深度学习中的注意力机制本质上模仿了人类处理复杂信息时的注意力，即从众多信息中获取最重要信息的能力。注意力机制能够使深度学习网络自适应地进行信息筛选，对重要程度更高的信息加以利用，并抑制其他无关信息，从而提高信息处理的效率和准确性。

本文在模型输出层之前添加注意力层，通过注意力层计算隐藏层中各神经元的权重，使网络主动聚焦隐藏层中的关键特征，来提高光伏发电预测的准确性。根据注意力权重计算方法的不同，可以将注意力机制分为两种：①由Bahdanau提出的加法模型；②由Luong 提出的乘法模型。两者区别在于加法模型使用第t-1 步的隐藏层状态计算第t步的注意力权重，而乘法模型则使用第t步的隐藏层状态进行计算。算例中将对两种注意力机制模型的效果进行对比，通过算例测试发现，加法注意力模型的光伏预测误差更小，因此本文使用加法模型构建注意力层。

3.4 MMoE-LSTM-Attention 网络结构

结合上述方法，本文设计的MMoE-LSTM-Attention网络结构如表1所示。

表1 MMoE-LSTM-Attention 网络结构Tab.1 Structure of MMoE-LSTM-Attention network

本文算例对区域内10 个光伏电站的趋势分量与剩余分量进行预测，因此子任务数为10。多任务层用于提取不同光伏电站出力之间的相关性，MMoE层可以自动实现关联性与子任务目标的信息分配，子任务层则利用了LSTM 层与注意力层实现了对每个光伏电站出力的预测。

4 算例分析

本文使用的数据来自澳大利亚DKASC 数据集[19]，从中选择了区域内10 个光伏电站2019 年全年光伏功率数据，采样率为每5 min 采样1 个数据点。输入特征包括前6 个点的光伏功率分解结果（包括6维趋势分量和6维剩余分量）和当前时刻的6个气象特征（包括温度、相对湿度、全局水平辐射、散射辐射、风向、降水），输入特征共18维。气象特征的采样率同样为每5 min 采样1 个数据点，预测对象为下一点的功率值，即滞后阶为1步。由于夜间光伏功率无需预测，为准确反映所提方法的有效性，本文仅采用日间功率数据进行训练与测试，时间段为07：00—18：00，共11×12=132 个功率点。将1月—11月数据作为训练集，12月数据作为测试集。为验证所提STL、MMoE多任务学习、注意力机制3方面技术改进有助于提升功率预测精度，下面采用控制变量的方法进行实验，即在对照方法中分别剔除STL分解、MMoE及注意力机制，以便准确分析所提方法效果，模型均训练50轮后进行预测。

4.1 STL 有效性分析

本文所提方法需要分别对STL 得到的趋势分量与剩余分量进行预测，之后再与周期分量相加得到最终预测结果。为测试STL 对光伏功率预测的影响，对比方法使用相同的网络结构直接对光伏功率进行预测，两种方法的误差情况如表2所示。由表2可知，在光伏功率预测中，STL能有效提高预测精度。在平均绝对误差MAE（mean absolute error）与均方根误差RMSE（root mean square error）两个误差指标上，经过STL的多任务学习模型预测误差更低。

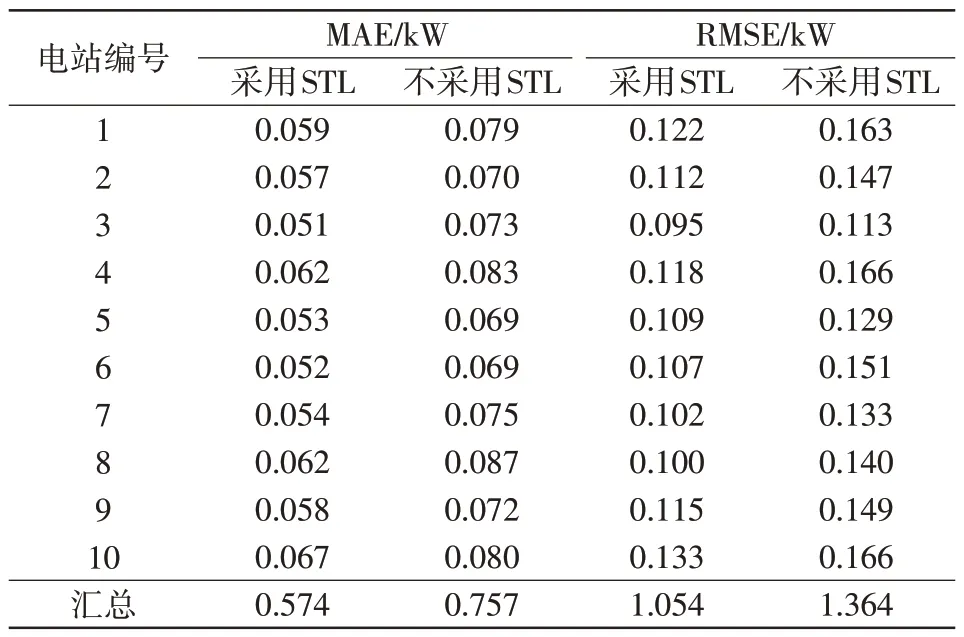
表2 STL 对预测误差影响Tab.2 Effect of STL on prediction errors

为进一步验证STL的优越性，保持模型其他环节不变，将STL 替换为多种分解算法，计算预测误差。对比方法包括集合经验模态分解、变分模态分解[6]和小波包分解[16]。根据中心频率法[6]确定集合经验模态分解数目为14，变分模态分解数目为10，小波包分解数目参考文献[16]设置为2，得到不同分解算法的误差对比如表3所示。

表3 不同分解算法的误差对比Tab.3 Comparison of errors among different decomposition methods

由表3可知，与其他先进分解算法相比，STL算法能有效降低模型预测误差。从算法原理来看，STL尤其适用于具有周期性的时间序列数据。而对于周期性的光伏功率序列，STL 得到的周期分量无需预测即可确保准确，趋势分量的波动性不强预测相对容易，剩余分量可通过多任务学习提高预测准确率，因此STL能够提高光伏功率的预测精度。

4.2 MMoE 多任务学习有效性分析

本节测试MMoE 多任务学习方法的有效性，选取单任务学习方案作为基准，即采用子任务层的网络结构分别训练模型进行预测。传统的硬共享机制多任务学习方法作为对比方法，在测试集上的预测误差如表4所示。

表4 多任务学习预测误差对比Tab.4 Comparison of prediction errors among different multi-task learning methods

由表4 可知，两种多任务学习的方法预测误差低于单任务学习方法，而本文所提基于MMoE的多任务学习方法比传统的硬共享机制多任务学习方法的误差更低，这表明MMoE 中的门控机制能够在子任务训练中实现不同任务信息的自动权衡，从而排除任务之间的无关因素，有助于提高预测精度。

4.3 注意力机制模型选择

注意力机制模型可分为加法模型和乘法模型两类，本节分别采用两种模型进行测试，不使用注意力机制的方法作为对照，网络的其他部分与表1 所示结构一致。3 种方法的误差结果如表5所示。

表5 不同注意力模型误差对比Tab.5 Comparison of errors among different attention models

由表5 可知，与不使用注意力机制相比，使用注意力机制的效果更好，而加法注意力机制能够使模型提取的特征更加突出，这可能是由于某个光伏电站与其他光伏电站之间的相关性特征具有可加性导致的。

4.4 预测误差分析

4.4.1 不同时间区间的预测误差分析

本节对测试集的预测误差进行分析，以小时为区间对预测误差取平均值，并以箱线图表示，结果如图6 所示。由图6 可知，整体预测误差约为0.5 kW，误差水平较低，验证了所提方法的有效性。而13：00—14：00 的预测误差明显高于其他时段，这是由于此时段的太阳辐射强度最高，放大了光伏功率的波动性，因此从绝对误差指标来看预测误差更高。

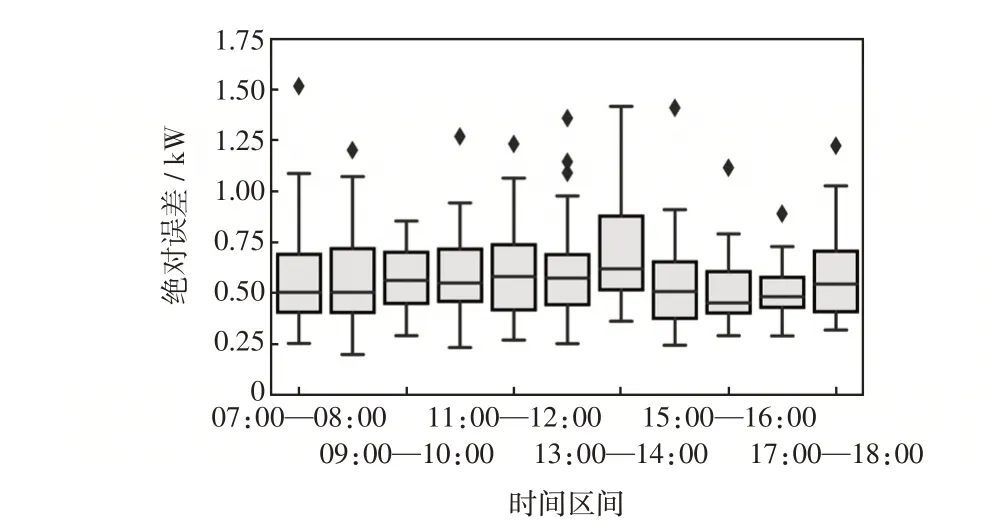
图6 不同时间区间的MAE 对比Fig.6 Comparison of MAE at different time intervals

4.4.2 不同季节、天气类型的预测误差分析

为验证所提模型在不同季节、不同天气类型下的预测性能，本节区分晴、多云、阴和雨/雪4种天气类型，并使用LSTM、EEMD-LSTM[7]和CNN-LSTM[9]作为对比方法，对数据集中的3 月（春季）、6 月（夏季）、9 月（秋季）和12 月（冬季）的光伏发电功率进行预测，其余数据作为训练集，得到MAE指标对比如表6所示。

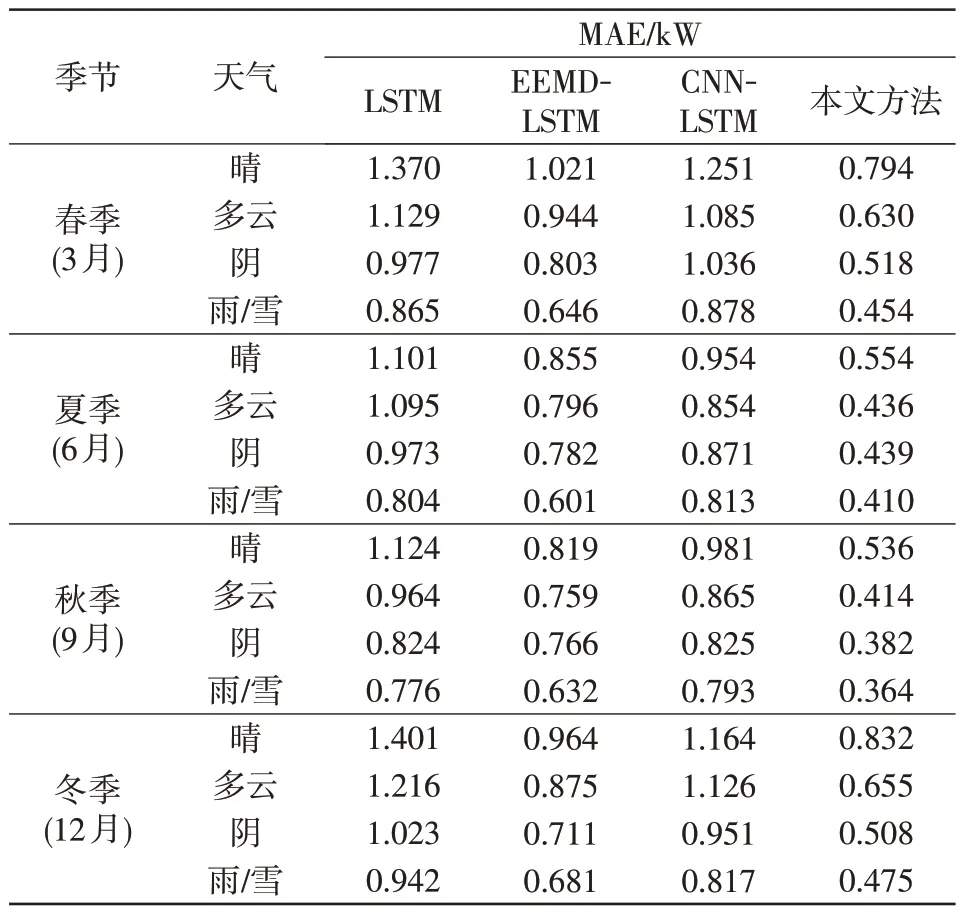
表6 不同季节、天气类型的MAE 指标对比Tab.6 Comparison of MAE under different seasons and different weathers

由表6可知，从季节因素来看，春季、冬季预测误差略高，夏季、秋季误差较低，原因是该地区春季、冬季气温较高，光伏功率总体数值偏大，预测绝对误差也相应增加。从天气类型类看，晴天光照充足，光伏发电功率较高，因此预测误差较高；多云、阴、雨/雪天气的光照逐渐降低，光伏发电功率减小，预测误差也相应降低。从4种方法的预测误差对比来看，CNN-LSTM 通过CNN 进行特征提取，增加了特征的有效性，预测误差较LSTM有所降低；经验模态分解EEMD（ensemble empirical mode decomposition）-LSTM 则对原始光伏功率进行分解，得到的模态分量规律性更强，易于预测，因此预测误差进一步下降；本文方法则使用STL对光伏功率序列进行分解，并通过MMoE多任务学习模型考虑区域光伏电站间的关联性，在4种对比方法中预测误差最低，验证了所提方法的有效性。

5 结论

本文提出了一种基于STL与MMoE多任务学习的区域多光伏电站功率联合预测方法。通过STL获得光伏功率的周期分量、剩余分量与趋势分量。对于区域多光伏电站，周期分量无需预测，而不同光伏电站的剩余分量与趋势分量之间存在关联性，可通过多任务学习进行预测。对此，本文提出了MMoE-LSTM-Attention 网络，来挖掘同一区域内不同光伏电站剩余分量与趋势分量之间的相关性，通过注意力机制改进深度神经网络模型进行预测。通过算例验证了所提方法的有效性。主要结论如下。

（1）与已有分解方法相比，STL更适合光伏功率这种周期时间序列数据，可解释性更好。分解得到的周期分量、趋势分量、剩余分量为后续建模预测提供了便利。

（2）MMoE 多任务学习能够有效考虑区域内不同光伏电站剩余分量与趋势分量之间的弱相关性，从而提高预测精度。此外，MMoE 多任务学习能够同时对多个光伏电站功率进行预测，降低了建模与计算成本。

（3）使用注意力机制对深度神经网络进行改进，进一步提高了模型的特征提取能力。算例中对比了加法注意力模型与乘法注意力模型，证明了加法注意力模型更适合光伏功率预测问题。