永磁起动/发电机在弱磁条件下磁场与涡流损耗分析

王晓远，梁慧静，李天元，赵晓晓

（天津大学电气自动化与信息工程学院，天津 300072）

集成起动/发电机ISG（integrated starter/generator）系统因其快速启停、质量轻、成本低、污染小及能量回收再利用等优点，广泛应用于电动汽车、航空航天、工业机床等领域[1-2]。内置式永磁同步电机IPMSM（interior permanent magnet synchronous motor）因其效率高、功率密度高、体积小等优点广泛应用于ISG电机系统[3]。

永磁起动/发电机PMISG（permanent magnet integrated starter/generator）在实际运行时，气隙中含有不同阶次谐波与旋转转子发生相对运动，在永磁体内产生大量涡流损耗[4]。与此同时，混合电动汽车空间有限，PMISG 轴向长度要求尽可能短，为缩短线圈端部长度常采用分数槽集中绕组形式，相比于整数槽绕组会产生更多的涡流损耗[5]。涡流损耗会引起永磁体温度升高，而车内空间狭小散热环境不良，过高的温度会造成永磁体退磁的恶劣影响[6]。电动汽车在起动过程中PMISG 工作在电动状态，带动发动机到达临界转速，此过程中采用了弱磁控制方法获取大转速，期间磁通会急剧变化，永磁体内涡流损耗也因此增大。在弱磁升速过程中，电机磁通饱和程度会发生变化，从而对dq轴电感及磁链等参数产生影响，同时对涡流损耗也会产生影响。电动状态的PMISG 在获得最大转矩时磁路会达到饱和状态，使得PMISG 成为一个非线性、多耦合的系统，永磁体的涡流损耗分析更加复杂。

永磁体涡流损耗直接影响电机效率和永磁体温度，为了提高效率、降低永磁体温度和避免退磁，针对各种类型电机的永磁体涡流损耗研究一直是众多学者研究的热点。Yamazaki等[7]研究了在脉宽调制PWM（pulse width modulation）控制模式下永磁同步电机在二维和三维模型中气隙磁场的谐波情况，以及各次谐波在转子永磁体所产生的涡流损耗，并进行了实验验证。Chen 等[8]探究了表贴式永磁同步电机中永磁体的厚度、充磁方式等因素对涡流损耗的影响。文献[9]分析了电动汽车用PMISG不同弱磁角与不同转速情况下的永磁体涡流损耗，但是没有考虑到弱磁条件下转速和超前角的相互联系，只进行了独立分析，没有对磁场的变化做进一步讨论。

综上所述，PMISG 在电动汽车领域的应用一直是研究热点，其在弱磁过程中的永磁体涡流损耗却少有研究。在电机实际运行的过程中，弱磁情况下电机磁场分布会发生变化，导致电感也随之变化。此外，弱磁运行下磁场分布的变化会造成感应在永磁体上的涡流发生变化，进而影响永磁体涡流损耗。因此，本文针对两种电机在弱磁运行下的永磁体涡流损耗与磁场进行分析研究，选取两台不同转子的35 kW内置式PMISG为研究对象，在定子结构完全相同、转子磁钢用量相同的条件下，比较了V 型和双V 型两种转子磁极结构的直交轴电感和永磁体涡流损耗。利用有限元法，选取额定电流和最大电流两种最具代表性的工况时的电感、永磁体涡流损耗与弱磁程度的关系进行了具体分析。最后制作样机进行实验并对仿真分析结果进行了验证。

1 PMISG 基本结构与参数

PMISG 选用了12 极18 槽的极槽配合，每对极下的结构和场量都相同，因此可选择1对极结构作为二维求解域模型，简化计算量，模型如图1 所示。转子磁极结构分别为V 型和双V 型。在定子完全相同的前提下，两种转子磁极结构具有相同的磁钢用量及分块数量。

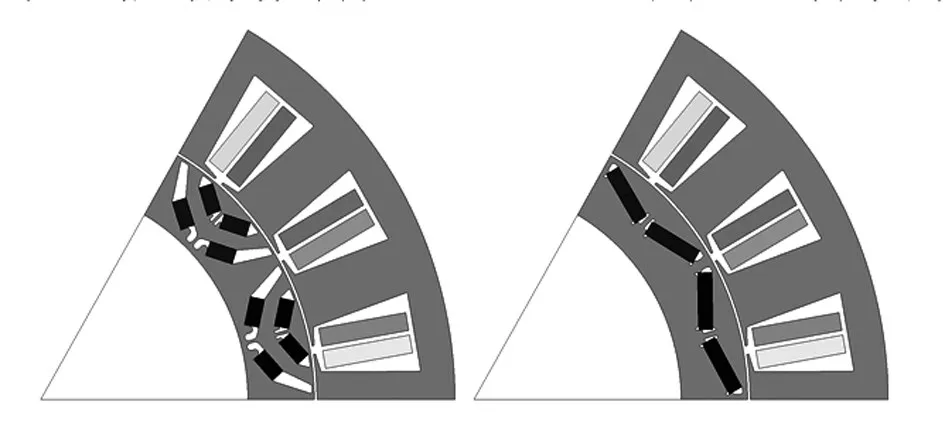
图1 PMISG 的1/6 转子结构模型Fig.1 Structural model of one sixth of PMISG rotor

混合动力汽车用PMISG的部分基本参数如表1所示。

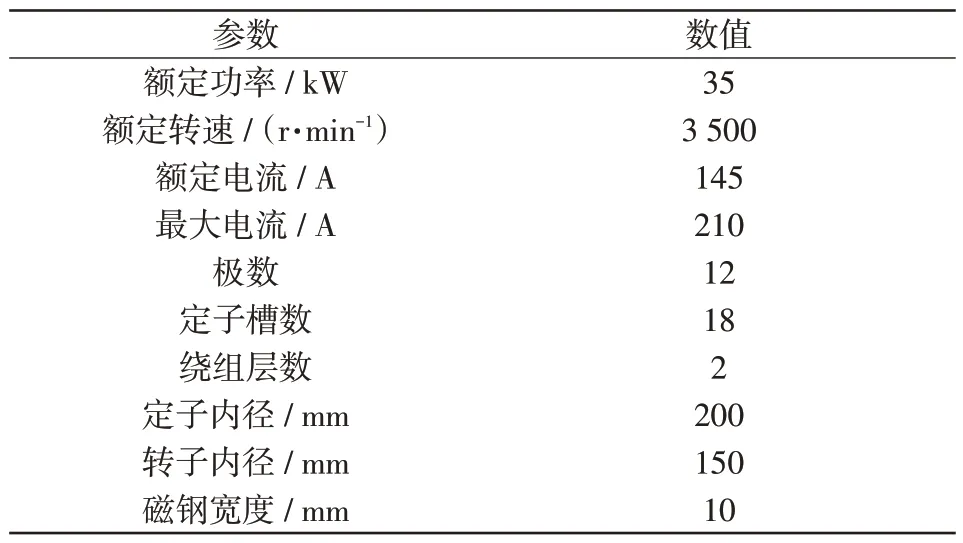
表1 PMISG 样机参数Tab.1 Parameters of PMISG prototype

2 PMISG 理论分析

对于轻型混合电动汽车，PMISG既作为电动机又作为发电机。PMISG 的发电工况已有很多学者进行研究，且在此工况的弱磁程度由所带负载决定，研究磁场变化与涡流损耗之间的关系十分重要。因此，本文对PMISG电动工况时弱磁条件下的涡流损耗进行研究。

2.1 弱磁控制原理

IPMSM 的dq轴磁路不对称，dq轴电感相差较大，为弱磁控制带来了很大优势[10]。IPMSM 运行过程电流、电压轨迹如图2所示。

图2 IPMSM 运行过程电流、电压轨迹Fig.2 Trajectories of current and voltage of IPMSM under operation

IPMSM弱磁工况时运行在图2中AC段。在AC段，dq轴电流满足

式中：irms为电流有效值；imax为最大受限电流；id、iq分别为dq轴电流。

dq轴电压满足

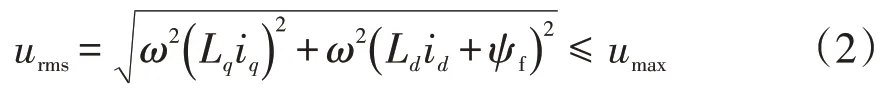
式中：urms为电压有效值；ω为转子旋转电角速度；umax为逆变器由直流母线电压得到的最大受限电压；ψf为永磁体磁链幅值；Ld、Lq分别为dq轴电感。

直轴电流id为

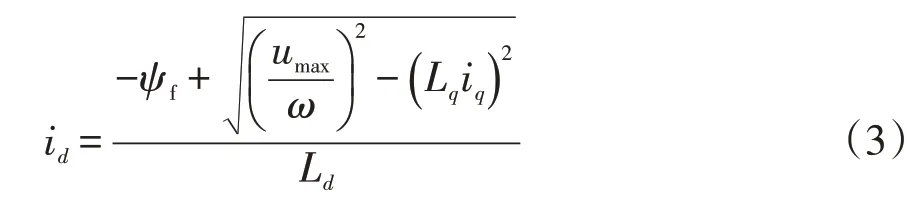
忽略定子电阻的影响，可推导出弱磁控制下的转速方程，即

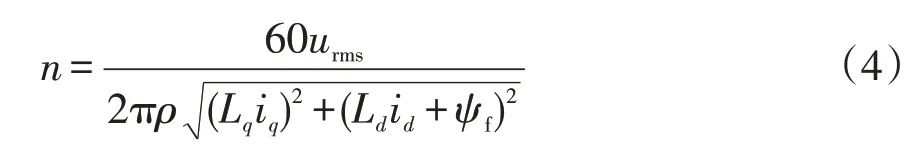
式中：n为转子转速；ρ为凸极率，

当电机运行在AC段弱磁控制工况下，转速已经超过基速，逆变器的电压极限输出为主要限制因素。此时，AC段dq轴电流与转速之间为一一对应的关系，即超前角与转速之间一一对应。

2.2 涡流损耗分析

对永磁体的涡流损耗进行计算，做如下假设：

（1）谐波磁通密度在空间按照正弦分布，忽略永磁体表面对谐波幅值削弱作用；

（2）永磁材料的磁导率μ为常数；

（3）磁场穿过永磁体是均匀分布的。

图3 为永磁体涡流损耗计算模型。其中，磁场方向与永磁体充磁方向相同，且在垂直平面Oxy内形成涡流，如虚线部分所示；a为永磁体轴向长度；b为宽度；dx、dy分别为涡流在x、y轴方向的长度微分；β为永磁体宽度与涡流回路直角的连线的夹角。

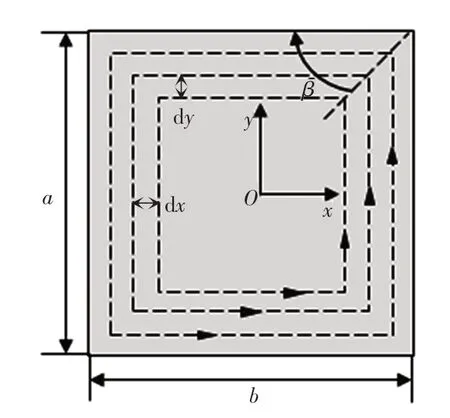
图3 永磁体涡流损耗计算模型Fig.3 Calculation model of permanent magnet eddy current loss

涡流环中y方向的有效长度用x表示，即

式中：y0为y方向上的初始长度；ky为正切系数；β为永磁体宽度与涡流回路直角的连线的夹角。

1个涡流环的磁通φ(x,t)可表示为

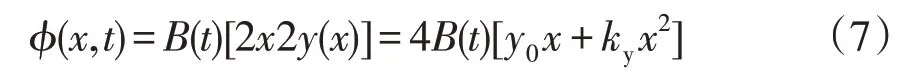
式中：B(t)为涡流环内磁通密度；y(x)为涡流环内y方向有效长度。涡流环内产生的感生电动势可表示为

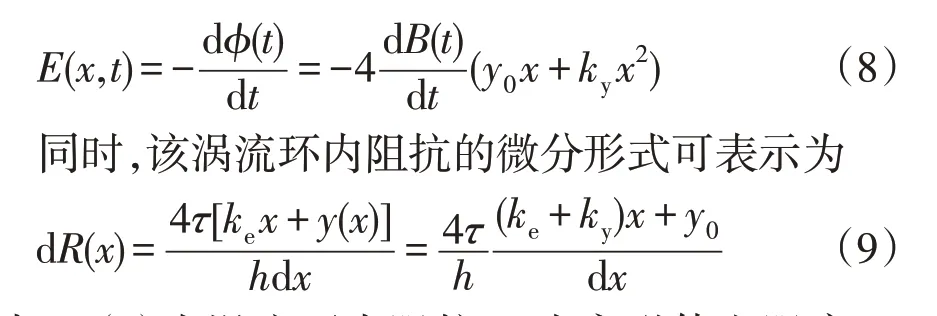
式中：R（x）为涡流环内阻抗；τ为永磁体电阻率；h为永磁体厚度；ke为端部效应有关的系数，其初始值为1。

永磁体上1个涡流环的功率损耗Peddy1可表示为

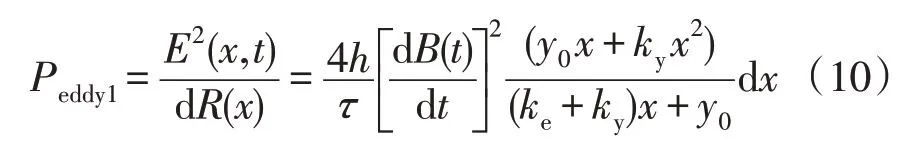
在x方向做积分可得整块永磁体的涡流损耗Peddy为

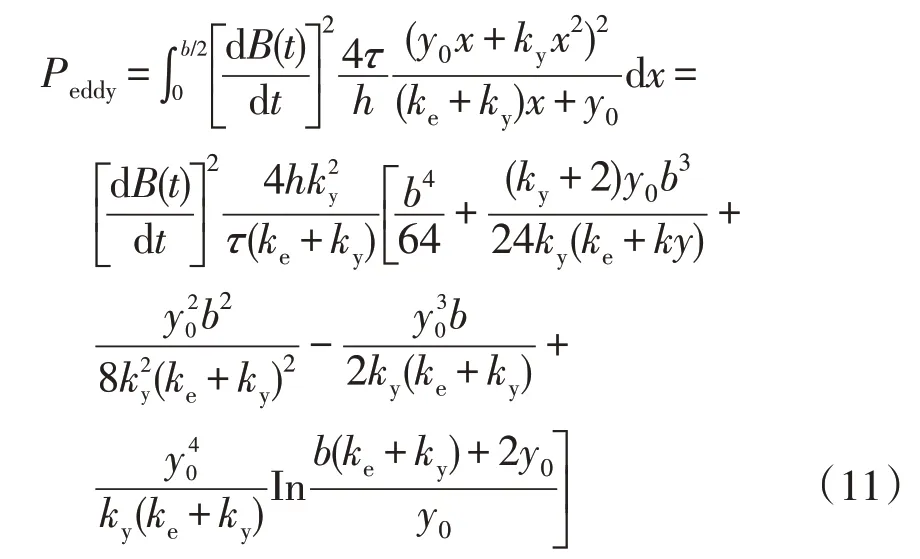
由式（11）可以看出，永磁体涡流损耗与其体积、厚度和磁密有关。在电机磁钢一定时，永磁体涡流损耗由磁通的交变频率与谐波含量决定。

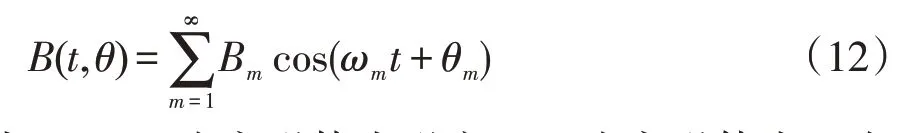
式中：B(t,θ)为永磁体内磁密；Bm为永磁体内m次谐波磁密幅值；ωm为m次谐波电角频率；θm为m次谐波相角。

本文谐波主要指由于电机结构（例如定子齿槽、转子结构、磁钢排布等）产生的空间谐波。涡流损耗不仅与弱磁角有关，还与Ld、Lq相关。

dq轴电感参数在电机控制中十分关键。PMISG 在较大负载时，磁路饱和、交叉耦合现象更为严重。根据电感定义，dq轴电枢反应电感为

式中：Mdq、Mqd为dq轴互感参数；ψd、ψq为dq轴磁链。

3 电磁性能计算与有限元验证

采用V 型和双V 型两种转子磁极结构的PMISG为样机，对PMISG空载与实际弱磁过程进行仿真分析。

3.1 空载仿真分析

V型和双V型两种转子结构电机的空载反电势如图4 所示。两种转子结构空载相反电势的有效值分别为74.28 V 和68.28 V，谐波畸变率分别为0.32和0.25。双V型转子结构电机的空载反电动势波形更接近正弦，谐波含量更少。

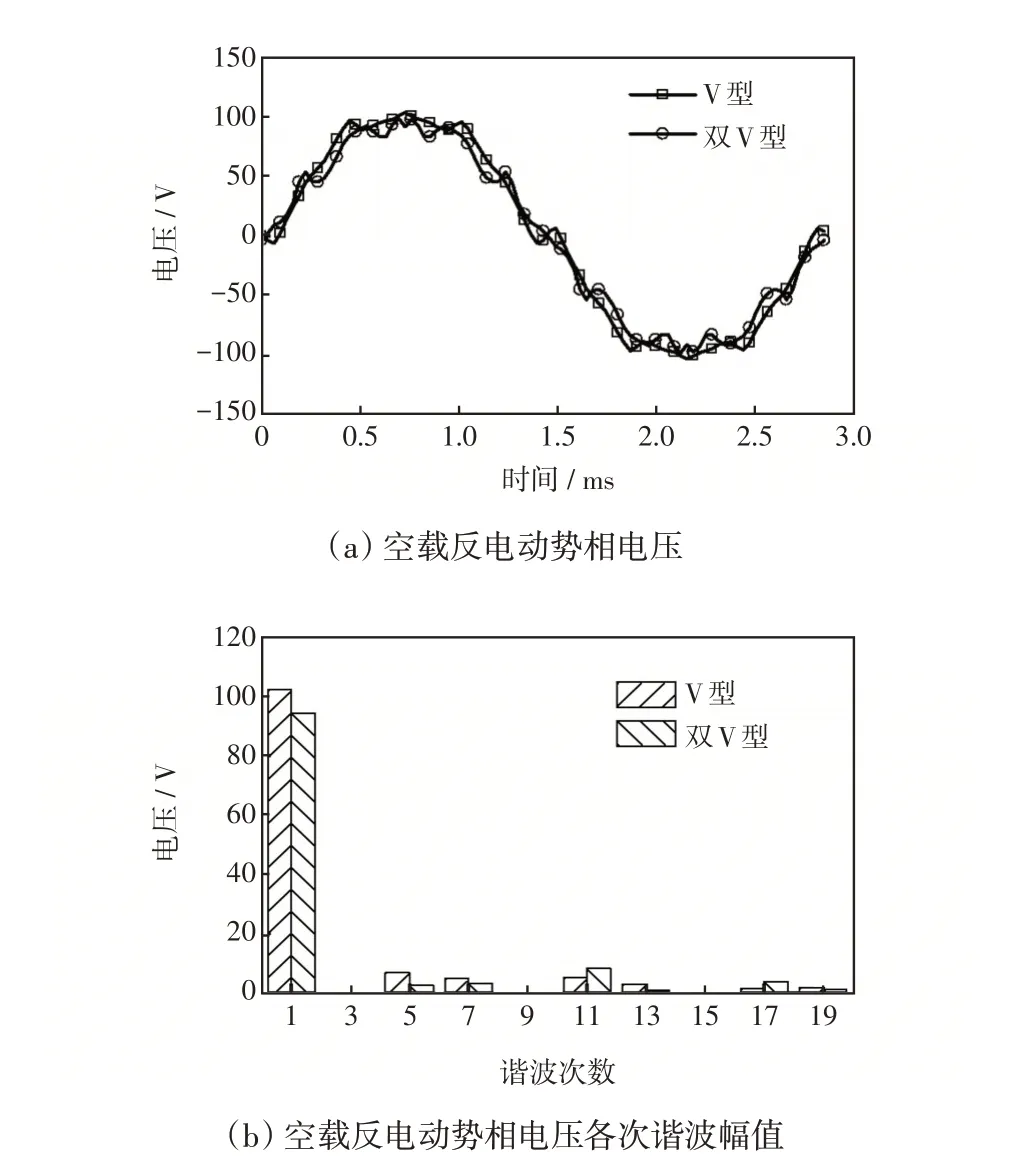
图4 空载反电势相电压及其傅里叶分解Fig.4 Phase voltage of no-load back EMF and its Fourier decomposition

两种转子磁极结构永磁同步电机的空载磁场分布如图5 所示，其中包含了电机磁力线分布、各部分剖分精度与磁密云图，证明了磁路设计与各部分剖分精度的合理性。

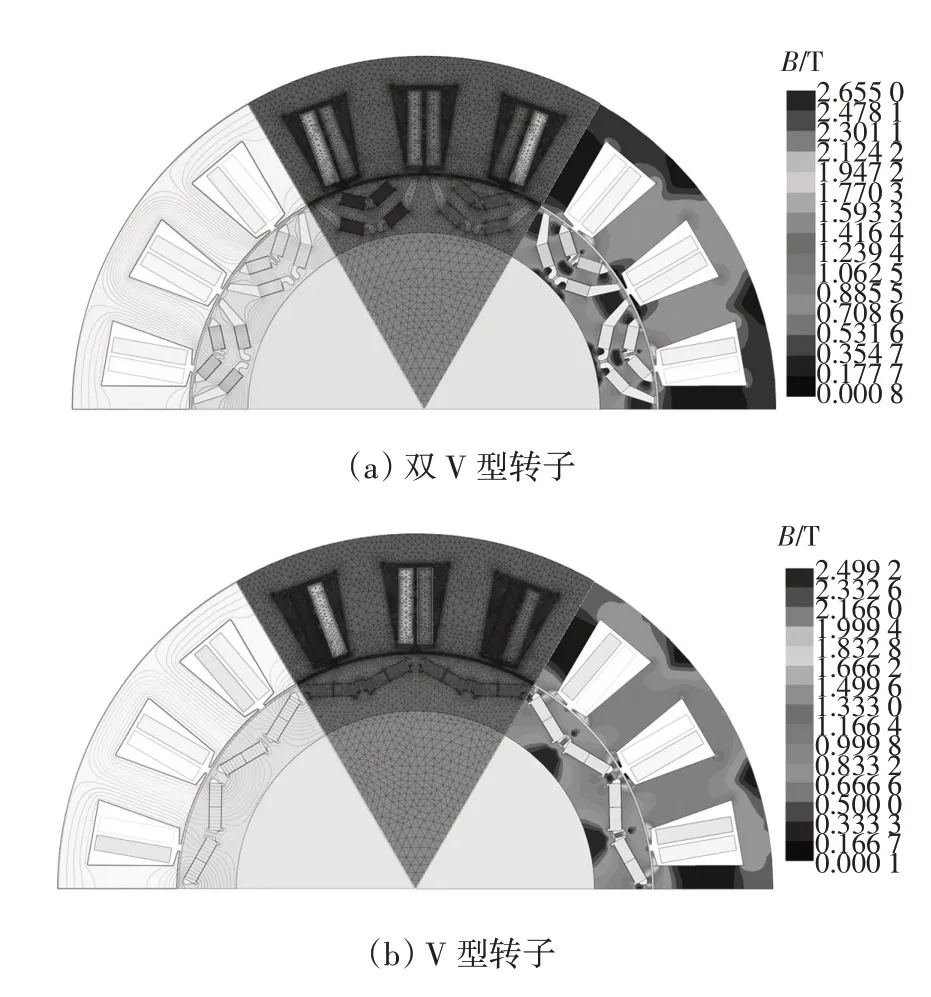
图5 两种转子磁极结构空载的磁场分布Fig.5 Magnetic field distribution of two types of rotor pole structure under no-load

3.2 弱磁条件下的电感与磁场分析

选取额定电流和最大电流两种工况进行研究分析，因为这两种工况最具有代表性。对于恒转矩阶段后的弱磁工况，由于此时已到达最大受限电压，为增大转速需要增大弱磁角度。此后，弱磁角与转速一一对应。每隔500 r/min取1个点，将弱磁角设置为变量，寻找其满足最大电压umax的弱磁角，仿真分析转速大于额定转速的运行工况。

图6 为在额定电流情况下两种转子结构电机不同弱磁条件下的dq轴电感。可以看出，双V型电机的交直轴电感差值大，弱磁性能更好。在电流一定的前提下，随着弱磁阶段升速，直轴去磁电流增大，直轴磁路磁密几乎保持在线性区域，所采用定子铁心材料磁化特性曲线的磁导率先增大后减小，因此直轴电感会随着弱磁程度的增大而略有降低；同时交轴电流减小，交轴磁路由饱和状态变为不饱和，交直轴磁路有重合部分，直轴磁通降低也有利于交轴磁路磁密处于线性区域，因此交轴电感在弱磁区域增大，这种影响在交轴磁路较饱和时更显著。双V 型PMISG 直轴磁路上的永磁体数比V 型的多1倍，因此直轴电感更小。

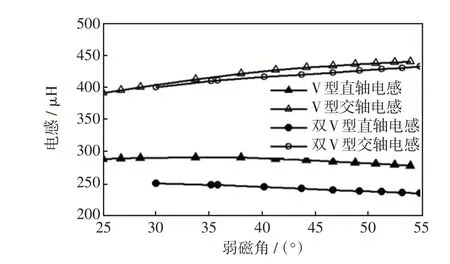
图6 额定电流时不同弱磁条件下的直交轴电感Fig.6 Direct and quadrature axis inductances under different field weakening conditions at rated current

图7 为最大电流情况下两种转子结构电机在不同弱磁条件下的dq轴电感。相比于额定电流工况，由于磁密由饱和变化到不饱和，磁通变化较大，电感变化的速率变大。最大电流工况的电感初始时要小很多，因为此时饱和程度深、电感小。随着磁密由饱和降到不饱和，交轴电感的变化速率也出现了明显增加，这是由于去磁电流的增大，削弱了交轴磁场。

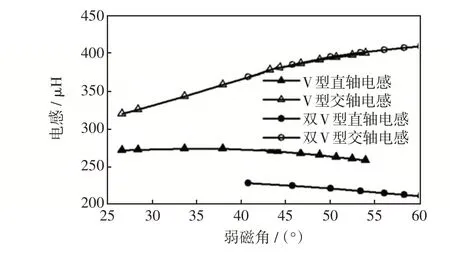
图7 最大电流时不同弱磁条件下的直交轴电感Fig.7 Direct and quadrature axis inductances under different field weakening conditions at maximum current

3.3 弱磁条件下的涡流损耗分析

图8和图9分别为额定电流工况与最大电流工况下两种转子结构在不同弱磁条件下的涡流损耗。

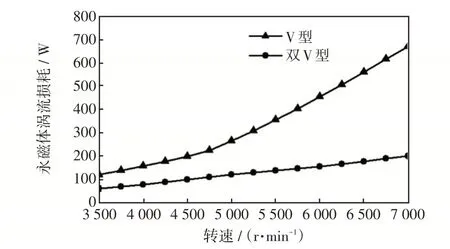
图8 额定电流时不同弱磁条件下的永磁体涡流损耗Fig.8 Permanent magnet eddy current loss under different field weakening conditions at rated current

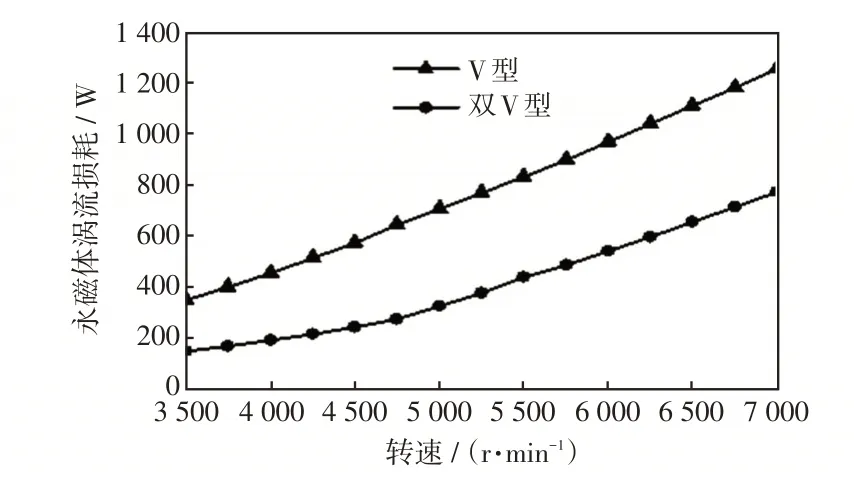
图9 最大电流时不同弱磁条件下的永磁体涡流损耗Fig.9 Permanent magnet eddy current loss under different field weakening conditions at maximum current

从图8 和图9 可以看出，双V 型转子的涡流损耗明显小于V型转子，这是由于双V型转子结构谐波含量更少。弱磁控制对交直轴磁场分布产生了影响，相应地永磁体内感应的涡流也发生了变化。饱和时磁密中谐波含量较多，随着交轴磁通饱和程度逐渐降低，永磁体涡流损耗变化速率会有所降低。弱磁过程对最大电流工况的双V 型结构电机永磁体涡流损耗的影响更加显著，在恒转矩阶段的拐点后更加明显，这是因为在最大电流工况下磁路饱和，而在额定电流工况下磁路是不饱和的。由于饱和强度深，双V 型弱磁作用更明显，因此双V 型永磁体涡流损耗的增速与转速不呈2次函数关系，而与磁场、电感、频率紧密相关，呈现出缓慢的1次增长趋势。双V 型PMISG 的交轴磁路磁通饱和程度较低，因此在弱磁阶段其涡流损耗的变化速率和恒转矩阶段接近。

4 实验验证

为了验证本文仿真分析的有效性，根据电机设计参数对本文所研究的V 型磁极结构转子PMISG进行了空载实验。图10为电机转子结构与样机装配图。图11 为样机实验平台。PMISG 与测功机相连，使用示波器记录空载反电势线电压。

图10 电机转子结构与电机装配Fig.10 Motor rotor structure and motor assembly

图11 样机实验平台Fig.11 Prototype test platform

PMISG永磁体涡流损耗不易直接测量，需要通过间接法计算。永磁材料在不同温度下会展现出不同的磁性能，根据其在空载状态下定子绕组中感应出的反电动势的变化程度，便可推出转子永磁体的温升情况，进而根据热力学原理计算永磁体涡流损耗。

在温度为T下定子反电动势的表达式[11]为

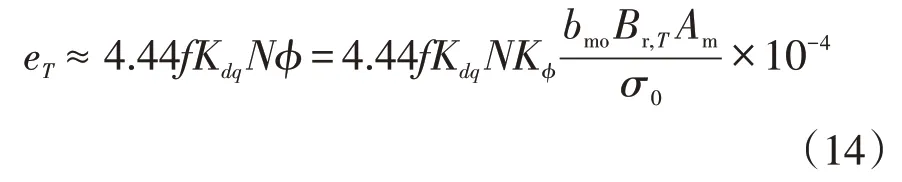
式中：eT为温度T下的定子反电势；f为电源频率；Kdq为绕组系数；φ为通过永磁体的磁通；Kφ为波形系数；N为绕组匝数；Br,T为温度T下的剩磁；Am为每极下永磁体面积；bmo为永磁体工作点；σ0为空载漏磁系数。其中，永磁体在温度为T1和T2时的剩磁关系为

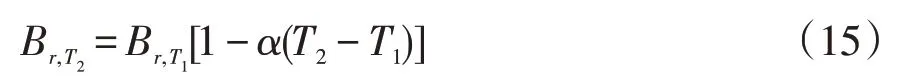
式中，α为永磁体温度系数。

由式（14）和式（15）可得，温升ΔT与反电势关系为

永磁体的涡流损耗表达式为

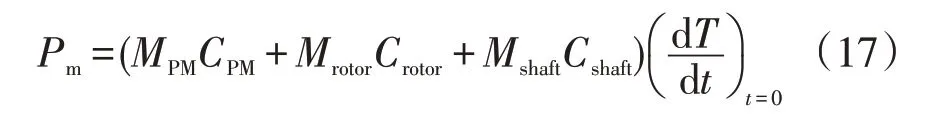
式中：Pm为永磁体涡流损耗；MPM为永磁体质量；CPM为永磁体比热容；Mrotor为转子铁心质量；Crotor为转子铁心比热容；Mshaft为转子转轴质量；Cshaft为转子转轴比热容。将式（16）代入式（17）可求得永磁体涡流损耗。

空载实验测量PMISG 在不同转速下运行的空载线反电势随时间的衰减情况。其中，在额定转速下运行35 min 空载线反电势随时间的衰减曲线如图12所示。

图12 转速为3 500 r/min 空载反电势下降法测量结果Fig.12 Measurement result of no-load back-EMF using drop method at rotation speed of 3 500 r/min

通过计算可得电机转速为3 500～7 000 r/min时的永磁体涡流损耗，并将其与仿真结果进行对比，如图13 所示。可见，实验结果比仿真结果大9%左右，原因是有限元仿真并未考虑电机端部效应，得到的涡流回路电阻较小；电机的制作工艺难以达到高精度，采用间接测量的方法会有误差。仿真结果与实验结果趋势相同，误差可以被接受，验证了本文分析的合理性。

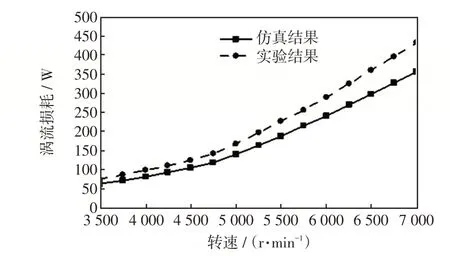
图13 涡流损耗实验结果与仿真结果对比Fig.13 Comparison of eddy current loss between experimental and simulation results

5 结论

本文以两台35 kW的内置式PMISG为例，在保证其他变量一致的前提下，对V型和双V型转子结构的PMISG 的空载状态和弱磁条件下的负载状态进行了有限元分析。分析了空载下磁路的合理性，并对两种转子结构的额定电流和最大电流情况下的dq轴电感和涡流损耗做了详细分析。通过样机进行实验验证，得到以下结论。

（1）在两台35 kW的电机永磁体用量与分块一致时，其空载反电势相接近，V型转子略大一些，这是由于双V 型磁极漏磁较大造成的。双V 型比V型获得的调速范围更广，这是因为双V型dq轴电感差值大，凸极率大。在永磁体涡流损耗方面，V 型转子结构电机的永磁体涡流损耗比双V 型转子大40%左右；在电感参数方面，交轴电感比直轴电感变化速率更大。

（2）对额定电流与最大电流下的弱磁控制时电机性能进行对比。在电感参数方面，电感变化率明显增大，这是因为在最大电流运行时，随着转速的增加，电机磁密由饱和变为不饱和状态，造成了电感的变化率变大。在永磁体涡流损耗方面，在最大电流运行时的永磁体涡流损耗明显增大，且双V型由于弱磁增长缓慢。在电机设计时，电机的弱磁能力主要由dq轴电感差值来决定，在速度增大的同时也要考虑电机的磁阻转矩与损耗问题。电机弱磁过程会对电机涡流损耗产生影响，弱磁过程会对谐波磁场产生影响，从而降低永磁体的涡流损耗。