Hf掺杂LaMnO3的第一性原理研究

吕书宇，李建伟，金浩，卫亚东，王健

深圳大学物理与光电工程学院，广东深圳518061

LaMnO3是带隙为1.10 eV 的A 型反铁磁（antiferromagnet，AFM）基态的钙钛矿半导体［1-3］，空间群为Pbnm，由锰（Mn）以及氧（O）组成的八面体之间以氧为交点规则排列，如图1 所示，沿着垂直c轴的Mn的各层间构成反铁磁耦合.通过对La位原子进行替换掺杂，可以调控改变晶体内部的原子位置、电荷分布、自旋排列等多种参数，在复杂的相互作用下，产生诸如庞磁电阻效应［4］、铁磁相变［5-6］以及绝缘体-金属相变［7］等有趣物理现象.目前，使用+2价的钙（Ca）、锶（Sr）、钡（Ba）等对LaMnO3进行p 型掺杂的实验以及理论计算研究已经比较深入，但对于用+4 价的锑（Sb）、锆（Zr）、镨（Pr）和碲（Te）等对La进行替换的n型掺杂来说，由于氧空位的影响难以排除，氧化物中反常霍尔效应又影响了电子载流子的测量，使人们一直质疑是否形成了真正的n型导电机制.近年来，WANG等［8-9］使用价态较为单一的Hf 掺入LaMnO3中，成功合成了稳定的La1-xHfxMnO3，并通过X 射线光电子能谱分析，证明了La1-xHfxMnO3锰氧化物中Hf 是以Hf4+形式存在.本研究从密度泛函理论的第一性原理出发，研究不同掺杂浓度下La1-xHfxMnO3的晶体结构和电子结构，以及其光吸收性质和同质自旋阀器件.

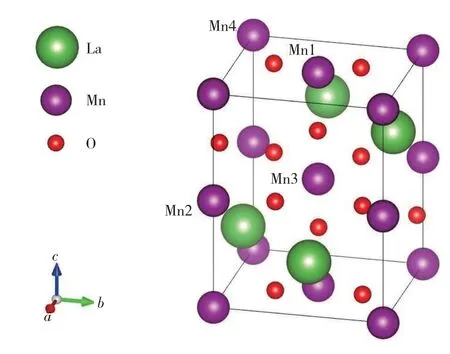
图1 正交晶系LaMnO3结构示意图（图中Mn1和Mn4与Mn2和Mn3分别位于相邻同一Mn层）Fig.1 The Schematic diagram of orthorhombic LaMnO3 structure.(Mn1 and Mn4 are in the same Mn layer perpendicular to the c-axis,while Mn2 and Mn3 are in the other nearest neighbor Mn layer.)

1 理论计算与LaMnO3基态确定

1.1 理论计算

本研究采用基于密度泛函理论的第一性原理计算软件包Vienna Ab-initio simulation package（VASP）进行结构计算，主要研究了锰氧化物钙钛矿LaMnO3以及其n 型掺杂La1-xHfxMnO3在不同掺杂浓度下的电子结构以及光吸收性质.在使用VASP 计算时，采用PBE 交换关联泛函［10］，同时使用了投影缀加平面波（projector augmented-wave，PAW）赝势［11］.计算中，Hf、Ba、La、Mn和O原子的价电子分别取为4 个电子（5d26s2）、10 个电子（5s25p66s2）、11 个电子（5s25p65d16s2）、7 个电子（3d54s2）和6 个电子（2s22p4）.使用Hubbard-U方法修正锰氧化物钙钛矿中Mn的3d轨道电子间库伦作用，其中VASP软件中的ldautype参数设置为4.平面波截断能取为450 eV.使用共轭梯度法优化结构，获得弛豫晶格常数及所有原子位置.当掺杂浓度x≤0.125时，进行扩胞计算，当扩胞到2×2×2后，结构优化时不再弛豫扩胞的晶胞长度.采用8 ×8×6的网格做倒空间k点采样（扩胞后，对应扩展方向的k点数目将减少）.晶格弛豫迭代过程中，设置原子间相互作用力的收敛标准为0.001 eV/nm，能量的收敛精度为1×10-5eV/原子.

为研究LaMnO3不同掺杂构成的同质结体系输运性质，采用基于NEGF-DFT的第一性原理计算软件包Nanodcal［12-13］计算了Ba 掺杂LaMnO3作为左右导线、Hf 掺杂LaMnO3作为中心层组成的自旋阀器件的磁电阻（magnetoresistance，MR），其中交换关联采用LDA +U方法，截断原子轨道基组采用Double-Zeta-Polarization，能量精度和截断能分别设置为1.0×10-5Hartree 和80 Hartree.计算透射系数时中心散射区k点设为6 × 6 × 1，导线偏压设为0 V.

1.2 LaMnO3基态

LaMnO3为过渡金属氧化物，在计算中需要引入自旋相反电子的强关联排斥能U，修正其Mn 原子中3d轨道电子的在位库伦能，使结果与实验相符 合.在VASP 中存在3种不同的加U方 法［14］：LIECHTENSTEIN 等［15］提出的旋转不变的局域自旋密度近似（local spin density approximation，LSDA）+U方法，DURAREV等提出的简化LSDA +U方法［16］，以及类似第一种但不考虑LSDA 交换劈裂方法［17］.为便于表述，本研究将这3种方法分别标记为LSDA +U-J、LSDA +（U-J）和LDA +U-J.其中，U为电子库伦相互作用项；J为交换相互作用项.LSDA+U-J方法与LSDA+（U-J）方法的区别在于前者的结果与U和J的取值都相关，而后者只与U-J相关.图2给出了3种加U方法下，反铁磁基态与铁磁基态的能量差ΔE=EAFM-EFM随着U值的变化.其中，J均设为0.5 eV.由图2 可见，3 种方法中，仅LDA+U-J方法给出LaMnO3的基态为反铁磁.在采用不同U的结构优化后，LDA+U-J方法下Ueff=U-J=5.0 eV 得到的晶格常数a=0.553 nm、b=0.586 nm 和c=0.768 nm 与实验结果［11-12］最一致.此外，3种加U下，Ueff=5.0 eV 得到的能带形状类似，带隙均约为1.10 eV［1］.综合考虑，后续的计算中均采用LDA+UJ，并取Ueff=5.0 eV.

图2 LaMnO3反铁磁基态与铁磁基态的能量差随Ueff的变化（J ≡0.5 eV）Fig.2 The energy difference between the AFM and ferromagnetic(FM)state of LaMnO3 as a function of Ueff(J ≡0.5 eV).

2 Hf掺杂LaMnO3

2.1 掺杂LaMnO3磁基态

图3 给出了La1-xHfxMnO3和La1-xBaxMnO3在不同掺杂浓度x下的反铁磁基态能量与铁磁基态能量之差.在掺杂Ba 的情况下，随着掺杂浓度的上升，反铁磁与铁磁态能量之间的差值ΔEBa在x从0.1 升至0.2 时由负转变为正，意味着发生了反铁磁相向铁磁相的相变，这与实验观察的结果相符［18］.从理论上说，当对LaMnO3进行p型掺杂（如掺Ca、Sr和Ba等元素）时，2 价阳离子替换了3 价阳离子，为使价态平衡，Mn4+的浓度随之升高.根据双交换作用机制［19］，Mn4+与Mn3+之间的交换作用会倾向于铁磁耦合.在图3 中，随着Ba 掺杂浓度上升，ΔEBa也不断上升，意味着Mn3+与Mn4+的铁磁耦合逐渐占据主导地位.对于La1-xHfxMnO3来说，ΔEHf始终小于0，说明反铁磁态始终是La1-xHfxMnO3的基态.按照n型掺杂的情况，掺杂Hf 会使体系内价电子数增多，根据价态守恒，Mn2+的数量将不断增加，由于Mn2+的d轨道为半满模型，增强了阳离子与阴离子之间半价键交换作用［20］，而半价键交换作用加深了Mn2+之间的反铁磁耦合程度，使得最终结果保持为反铁磁基态.

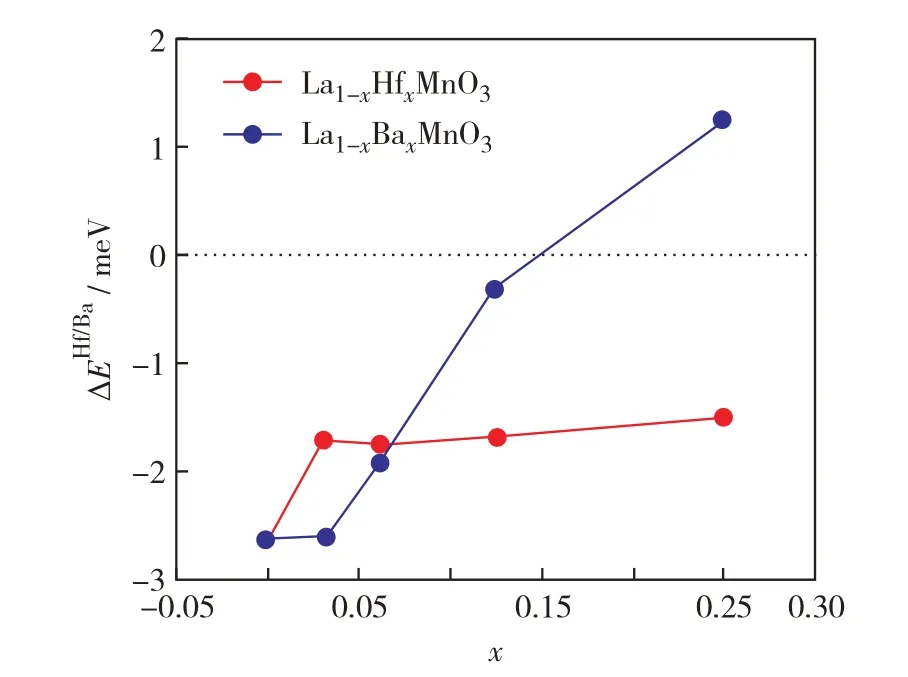
图3 La1-xHfxMnO3和La1-xBaxMnO3反铁磁态基态与铁磁态基态的能量差随着掺杂浓度的变化Fig.3 The energy difference between the AFM and FM state as a function of x in La1-xHfxMnO3(red line)and La1-xBaxMnO3(blue line).

2.2 晶体结构

当x为0.025、0.500和0.750时，以20个原子组成的Pbnm 空间群的LaMnO3原胞作为基本结构，并用Hf 分别替换1～3 个La 原子.当x为0.125、0.063、0.031、0.021 和0.014 时，分别将原胞进行 1 × 1 × 2、1 × 2 × 2、2 × 2 × 2、3 × 2 × 2 和3 × 3 × 2 等比例扩胞后再用Hf 替换1 个La 原子进行掺杂计算.结构优化时，当x≥0.031 时，扩胞的晶胞长度和原子位置一起弛豫；当x为0.021 或0.014时，由于掺杂浓度较低，只优化了原子位置，不变动扩胞的晶格常数.

表1列出了x从0增至0.750时各结构驰豫后扩胞长度折合到晶格常数的值，以及掺杂原子Hf 与最近邻O 原子间距和Mn—O—Mn 键角.由表1 可见，当x∈[0.031，0.750]时，扩胞长度折合后的晶格常数相比未掺杂结构发生了明显变化.比较晶格常数可以发现，随着x的上升，a和b长度逐渐变短，c逐渐变长，这意味着该正交晶系钙钛矿在a轴和b轴构成的ab平面内被压缩，而在c轴方向被伸长，原因是Hf 的离子半径小于La 的离子半径，在进行替换后，八面体之间的相互作用失去平衡，使钙钛矿结构产生畸变.

表1 La1-xHfxMnO3的晶格常数、Hf—O键长和Mn—O—Mn键角Table 1 The lattice constants,Hf—O bond lengths and Mn—O—Mn bond angles of La1-xHfxMnO3

2.3 电子结构

图4 为不同x下La1-xHfxMnO3的能带图.由图4可见，当x=0时，LaMnO3为半导体，带隙为1.10 eV，自旋向上和向下能带简并，与GONG等［1］的实验结果相符.在x=0.250、0.500、0.750 时，Hf的掺入对于能带结构的影响很大.当x=0.750时，75%的La 被Hf 替代，虽然体系仍是半导体，但其上下自旋能带不再简并，价带顶为自旋向上，导带底为自旋向下；当x=0.500时，体系变成了上下自旋简并的半导体，带隙为1.11 eV；而当x=0.250时，上下自旋能带简并再次解除，导带底和价带顶均由下自旋电子能级提供.这种现象源于Hf 的价电子改变了Mn原子在体系中的价态.在LaMnO3中Mn 离子为+3 价，3d 轨道上有4 个电子，按照洪德规则，这4个电子的自旋相同，锰氧化物钙钛矿的磁性也主要来源于Mn离子上3d轨道的电子自旋.

表2 列举了La1-xHfxMnO3中Mn 层的磁矩(m).由表2可知，当x=0时，各个Mn上磁矩的绝对值均为3.673μB（μB为玻尔磁子），构成LaMnO3的A型反铁磁结构，位于同一Mn层的Mn1和Mn4（图1）的磁矩为正，位于相邻Mn 层的Mn2 和Mn3 的磁矩为负，总磁矩为0.在替换1 个La 原子后，Mn1 和Mn4的磁矩几乎没有变化，而在负磁矩层中Mn2和Mn3的磁矩绝对值增加.其中，Mn2上磁矩的绝对值为3.837μB，比原来的3.673μB增加较小，而Mn3 上磁矩的绝对值变化较大，增加了约0.8μB，形成了亚铁磁半导体.因此，可以合理推测，替换1个La后，Hf4+会给体系多带来1个电子，这个电子通过交换作用基本转移到了Mn3 的3d 轨道上，令Mn3上磁矩的绝对值增大.而当替换2 个La 原子（x=0.500）时，多余的2 个电子分别转移到了不同Mn层自旋相反的Mn1 和Mn3 上（表2 第1 和第3 列），使得自旋能带再次简并，总磁矩为0.

表2 La1-xHfxMnO3中Mn的磁矩Table 2 Magnetic moment of Mn in La1-xHfxMnO3

当x为0.250～0.014 时，体系为20～360 个原子的LaMnO3超胞各用1 个Hf 替换1 个La 原子.当x＜0.063 后，掺入Hf 比较少，在能带中间逐渐孤立出1 条掺杂导致的杂质能带，而带隙基本保持在～1.13 eV，见图4（f）至（h）.

图4 La1-xHfxMnO3的能带图（a）x=0.750；（b）x=0.500；（c）x=0.250；（d）x=0.125；（e）x=0.063；（f）x=0.031；（g）x=0.021；（h）x=0.014；（i）x=0（红色为自旋向上的能带；蓝色为自旋向下的能带.）Fig.4 Band structures of La1-xHfxMnO3 for(a)x=0.750,(b)x=0.500,(c)x=0.250,(d)x=0.125,(e)x=0.063,(f)x=0.031,(g)x=0.021,(h)x=0.014,(i)x=0.(Red and blue lines represent the band structures with spin up and spin down states,respectively.)

为进一步探索La1-xHfxMnO3内部的物理机制以及掺杂带来的影响，以La0.969Hf0.031MnO3为例计算并分析其部分态密度（partial density of states，PDOS）.图5 给出了电子能量E=[ -1.0，1.0] eV 时各元素的PDOS 组成.其中，PDOS ＞0的部分为上自旋态密度；PDOS ＜0的部分为下自旋态密度；费密能级设置在Ef=0 处.在图5 中-0.1 eV 处存在一个主要由Mn和O组成的只有下自旋的DOS，对应图4（f）的能隙中的孤立能级.进一步计算表明，该孤立态密度主要源自与Hf最近的8个Mn的其中之一，以及与其相近的O原子，该Mn的价态由+3变为+2价，磁矩绝对值也由3.680μB变为4.447μB.同时，无论掺杂浓度是多少，Hf 的磁矩始终≤0.01μB，因此，可认为Hf 的4 个价电子全部转移出去，Hf以+4价离子存在于体系中.

图5 La0.969Hf0.031MnO3中各元素的部分态密度图Fig.5 Partial density of states of Hf,La,Mn,and O in La0.969Hf0.031MnO3.

3 La1-xHfxMnO3光学性质

为探究La1-xHfxMnO3的光学性质，采用原子尺度材料模拟的计算机程序包（Vienna Ab-initio simulation package，VASP）计算介电函数，并使用式（1）计算光吸收系数.

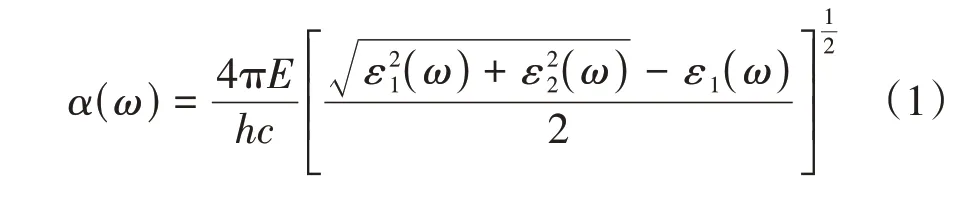
其中，ω为光照频率；ε1(ω)和ε2(ω)是介电函数的实部和虚部；h为普朗克常数；c为真空中的光速；E为电子能量.

图6 是利用式（1）计算得到的E在0～3.5 eV 时的La1-xHfxMnO3光吸收谱.对于本征LaMnO3即x=0时的结构而言，其光吸收带边大约位于1.3 eV 处，并且只有1 个位于2.2 eV 处的吸收峰.随着x从0增至0.125，光吸收边逐渐发生红移，而吸收峰的位置也缓慢左移，吸收峰的高度逐渐下降.当x=0.014、0.021和0.031时，光吸收边红移现象并不明显，但当x=0.063和0.125时，光吸收边发生较大偏离.

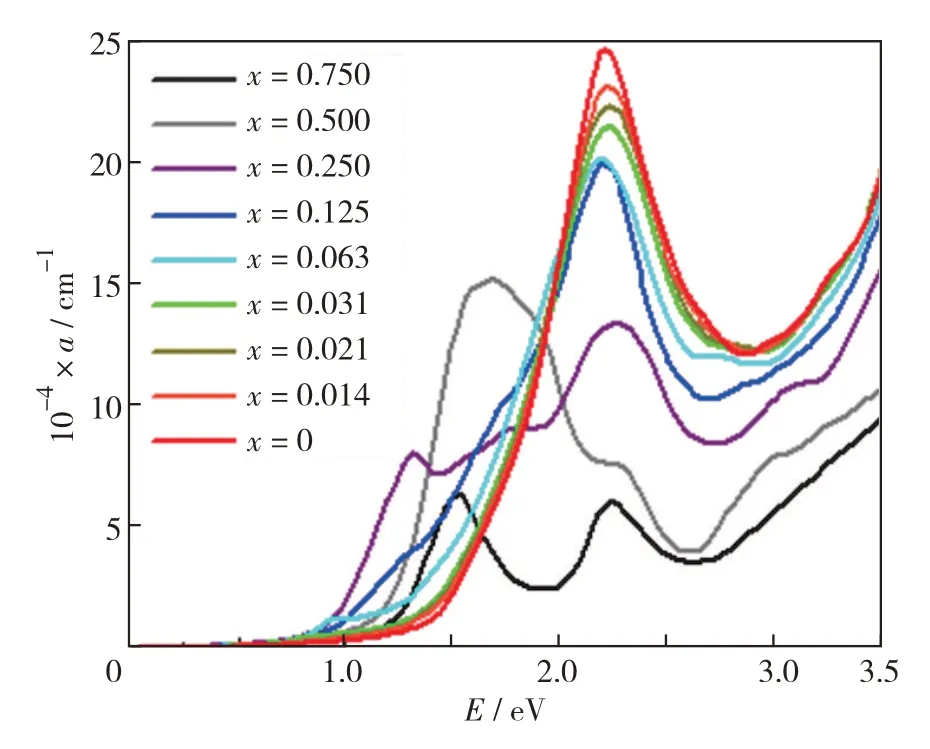
图6 La1-xHfxMnO3的光吸收系数图谱Fig.6 Absorption coefficient spectra of La1-xHfxMnO3.

当x=0.250、0.500 和0.750 时，由于结构变化较大，体系La1-xHfxMnO3的电子结构与LaMnO3相差较大，他们之间的光吸收也改变较大，吸收边发生大幅红移.当x=0.250和0.750时，光吸收曲线出现2个吸收峰；而x=0.500时，主要吸收峰又变为1 个.图4 能带图表明，x=0.250 和0.750 时，自旋劈裂，而x=0.500 时，自旋简并，说明光吸收图谱中的吸收峰与自旋劈裂的情况可能有关.

图7给出了不同掺杂浓度下La1-xHfxMnO3的光学带隙（Eoptg）.由图7 可见，本征LaMnO3的光学带隙为1.28 eV［21］，随着x的上升，La1-xHfxMnO3的光学带隙不断降低.其中，x分别为0.014、0.021、0.031、0.063、0.125 时对应的光学带隙分别为1.205、1.194、1.140、0.948和0.928 eV.可以发现，当x≥0.063 后，光学带隙下降明显.根据图4，当x在0.014～0.032 时，掺杂浓度较小，形成了孤立杂质能级，此时掺杂对体系的光学性质影响较小.而当x为0.063和0.125时，掺杂浓度变大，随之而来的是掺杂能级扩展成杂质能带，并使Hf逐步脱离掺杂地位，成为系统的主体元素之一，体系形成新的价带，使得带隙发生改变，从而显著改变了La1-xHfxMnO3的光学带隙.

图7 La1-xHfxMnO3的光学带隙Fig.7 Optical band gap of La1-xHfxMnO3.

3 LaMnO3掺杂体系在自旋阀中的应用

通过掺杂构造同质自旋阀具有很高的应用价值［22-23］.在本研究中，同质LaMnO3自旋阀由Ba 掺杂LaMnO3作为左右导线，中间夹Hf掺杂LaMnO3的三明治构成.计算中，半无限长左导线和半无限长右导线由La3/4Ba1/4MnO3给出；中心散射区由左右两边各有1 层La3/4Ba1/4MnO3原胞作为缓冲区与导线相接，中间为2 层La3/4Hf1/4MnO3构成.图8 给出了中心散射区示意.当两边导线的Ba掺杂La3/4Ba1/4MnO3（包括缓冲层）与中间的Hf掺杂La3/4Hf1/4MnO3磁矩朝向相同时，自旋阀为平行结构（记为P），此时电导较高，而磁矩相反时为反平行结构（记为AP），电导较低，平行或反平行结构可通过对中间层和导线加同向或者反向磁场控制.对中心La3/4Hf1/4MnO3加门电压Vg进行调控，可以通过改变电子透射系数获得更好的自旋阀效果.

图8 由La3/4Hf1/4MnO3和La3/4Ba1/4MnO3组成的自旋阀中心散射区（青色球体为Ba；黄色为Hf；绿色为La；紫色为Mn；红色为O；箭头代表磁矩朝向；c方向为电子传输方向）Fig.8 The scattering region of the spin valve formed by La3/4Hf1/4MnO3 and La3/4Ba1/4MnO3，in which cyan，yellow，green，and purple represent Ba，Hf，La，and Mn elements，respectively.Arrow means magnetic direction and c is along the electron transportation direction.

费密能级电子透射系数T在P构型和AP构型下随门电压Vg的变化如图9（a）.由图9（a）可见，随着Vg的升高，无论是P还是AP构型，T都会发生明显改变，当Vg处于-1.0～0.8 V 时，P 排列的电子透射率都高于AP 排列，且在Vg为0.3 eV 和0.6 eV 处分别存在2个峰值.

自旋阀的性能主要取决于费密能级处器件的磁电阻，计算式［24］为

其中，TP和TAP分别为P和AP构型的费密能级处的透射系数.由图9（b）可知，当Vg处于-1.0～0.2 V时，P 构型的透射系数比AP 排列大几个数量级，对应的MR 值非常高，有很好的自旋阀效果.在Vg=0 时，MR 值达到了～（2.8 × 105）%，在Vg=0.2 eV处可提升到～（5.1×105）%.

图9 （a）P和AP构型中费密能级处的透射系数；（b）费密能级处磁电阻MR随门电压Vg的变化趋势Fig.9 (a)Transmission coefficients for P and AP configurations,and(b)MR versus Vg at the Fermi energy.

结语

基于第一性原理通过计算研究了不同掺杂浓度La1-xHfxMnO3的晶格参数和电子结构.结果表明，La1-xHfxMnO3的基态为反铁磁基态或者亚铁磁基态，且能带结构皆为半导体，体现出n 型掺杂的性质.磁矩计算表明Hf 以稳定的+4 价出现，Hf4+替换La3+后，多余电子转移至相邻的1 个Mn 离子上.光吸收图谱表明，随着x的上升，La1-xHfxMnO3的光学带隙在不断下降，与能带结构密切相关.通过掺杂可以构成优异的同质LaMnO3自旋阀器件，器件磁电阻可达105%.