基于循环迭代粒子群算法对电动汽车无线充电系统的联合参数在线辨识

刘廷章 张子恒

基于循环迭代粒子群算法对电动汽车无线充电系统的联合参数在线辨识

刘廷章 张子恒

（上海大学机电工程与自动化学院 上海 200444）

无线电能传输系统中参数的偏移往往会影响系统的充电效率和传输功率。该文提出一种谐振式无线充电系统的联合参数在线辨识方法。首先根据等效谐振电路建立电路方程。其次建立特征量的模型。然后检测一次侧输入电压，一次侧实时电流和二次侧实时电流并对其进行傅里叶变换得出特征频率，在此基础上构造出只含有4个未知数（1、1、2、2）的适应度函数，将参数辨识问题转化为函数寻优问题。该文提出一种循环迭代粒子群算法来寻找最优解。将4个待辨识参数分为两组，1、1为第一组，2、2为第二组，每一次只辨识一组参数，然后将辨识结果作为另外一组参数寻优过程的初始条件进行循环辨识。除此之外，每一次辨识都会根据参数之间的灵敏度关系来迭代调整适应度函数。最后通过仿真和实验表明，所提的方案能够在无线电能传输系统中4个参数同时偏移的情况下有效辨识出各个参数，并且所提出的方法能达到较高精度。

参数偏移 无线电能传输 联合参数在线辨识 循环迭代粒子群优化

0 引言

近年来，由于环境污染和能源浪费的问题越来越严重，节能环保的电动汽车受到了社会各界的广泛关注，电动汽车的推广也得到了许多国家和车企的大力支持。但是与普通燃油车相比，电动汽车充电时间长、充电过程不方便等因素很大程度上限制了它的发展和推广[1]。电动汽车传统的充电方式是用电缆和接口连接起来对汽车进行充电，操作起来比较麻烦。电动汽车无线充电技术通过埋于地面下的供电导轨以高频交变磁场的形式将电能传输给运行在地面上一定范围内的车辆接收端电能拾取机构，进而给车载储能设备供电。无线充电的方式与传统的有线充电方式相比，更加安全、可靠和灵活[2]。

现今，电动汽车的无线充电技术大体分为电磁辐射式充电、电磁感应式充电以及电磁耦合谐振式充电，其中电磁耦合谐振式无线电能传输（Magnetically- Coupled Resonant Wireless Power Transfer, MCR- WPT）技术具有传输距离远、安全性能好以及传输效率高等特点，被广泛地应用在电动汽车的无线充电方面[3-6]。文献[7-9]讨论了电磁耦合谐振式无线充电系统的设计，在实际情况中，汽车通过特定的充电路段时，输入为指定的谐振频率，在高频交变信号和两侧的谐振电路共同作用下，一次和二次线圈在相同的谐振频率下会产生谐振现象，此时整个系统的充电效率达到最高。

在MCR-WPT系统中，影响电动汽车充电效率的主要原因可以分为两类；第一类是线圈位置和距离的改变引起互感的改变，从而导致充电效率的降低；第二类是由于谐振电路参数长期衰减导致的软故障使系统偏离谐振工作点。由于外界恶劣环境的各种影响，埋在地下较长时间的一次线圈电感值可能会发生偏移。整个系统的其他电路元件参数，如一次侧电容和二次侧电容也可能随时间发生不同程度的漂移。一旦出现这些问题，电磁耦合谐振电路就会脱离原来的谐振状态，导致整个无线电能传输（Wireless Power Transfer, WPT）系统充电效率大大降低，造成大量的能量浪费，甚至会引起电流激增，从而导致更严重的事故。然而，工业现场的电路参数不易进行现场测量，因此在线辨识WPT系统的参数并对其及时校正具有重要的意义和研究价值。本文主要研究电路参数长期衰减引起的系统软故障。

确定电路系统未知参数的第一种方法是解析法。根据电路的拓扑结构列出相应的电路方程，建立数学模型，对于电路结构简单、电路参数较少的模型，可以直接计算出未知参数的解析解[10]。已有许多的研究人员对WPT系统的各种参数提出了不同的辨识方法。文献[11-14]都是通过数学关系对系统的互感和负载进行辨识。文献[11]通过开关工作频率检测输入电压、电流以及它们之间的相位差，然后根据稳态特性计算负载等效阻抗和互感系数；文献[12]提出了一种基于开关工作频率的在线参数辨识方法，并建立负载和互感系数的数学模型；与文献[11-12]不同的是，文献[13]通过在系统中附加一个电容，使IPT系统工作在两种不同的运行状态，并分别建立数学模型来对负载阻抗和互感系数进行辨识；文献[14]提出只需要测量一次电流，利用基于状态估计的参数识别算法，在充分考虑信息冗余的情况下，准确估计耦合系数和负载。文献[15]提出了一种矩形线圈互感计算方法，运用提出的互感计算方法，分析了该线圈结构的互感特性。文献[16]针对LCT的互感求解问题展开研究，运用毕奥萨伐尔定律建立该结构的互感计算模型。此外，一些学者还提出了一些基于阻抗分析法和功率守恒原 理[17-18]的负载参数辨识方法。在文献[18]中通过测量一次线圈谐振电流和电压，利用正交变换算法和反射阻抗理论计算有功功率，再利用有功功率计算负载电阻。也有相关的文献专门针对WPT系统的负载参数提出了辨识方法[19-21]。文献[19]通过建立WPT系统基-谐波模型，提出了一种多负载参数联合识别方法来对电源电压、等效负载阻抗进行辨识。文献[22]提出了对于一个8线圈WPT系统的负载信息进行识别的方法，该方法需要计算或者测量各绕组自感、互感以及谐振电容值。在实际的WPT系统中，两侧线圈的距离和相对位置的变化也会引起互感值的变化[23-24]。文献[23]通过灵敏度分析，在WPT系统中选取了较好的互感识别模型，得到了具有较好鲁棒性的辨识模型。文献[25]提出了一种DC-DC WPT系统的参数识别方法，可以在参数偏移和不同负载条件下，只需得到一次侧信息就可辨识互感、输出电压、输出功率和效率等参数。利用传统的方法对WPT系统进行参数辨识经常会出现多解的情况[26]。文献[27-28]分别提出了不同的解决办法来消除非期望解。文献[27]讨论了如何对WPT系统中耦合系数进行辨识，通过推导每一次都会辨识出两个解，其中一个非期望解，通过改变系统输入电压，得到不同的辨识值，选取最接近的两个值的平均值作为辨识结果；文献[28]提出了一种利用励磁机组的多直流信息进行多耦合系数识别的方法，该方法可以避免出现多解问题。以上文献提出的方法最终都是通过计算方程的解析解来达到参数识别的目的，然而，对于具有复杂数学模型和未知参数较多的系统，用解析方法往往很难甚至无法找到解析解。

对于多参数的高阶非线性系统，常采用数值方法辨识未知参数[29]。它的基本原理是利用大量的样本数据通过参数识别方法确定未知参数。最常用的参数辨识方法是最小二乘法。文献[30]提出了一种基于最小二乘法的自感系数参数辨识方法，解决了自感系数的模糊辨识问题。文献[31]用传递函数分析了WPT系统的动力学特性并且利用递推最小二乘法滤波来对线圈耦合系数进行参数辨识。文献[32]通过测量输入阻抗，利用Newton-Raphson方法对两个非线性极值方程求解，得到互感系数的迭代解。对于参数较多的高阶非线性系统，往往利用智能优化算法将参数辨识问题转化为函数的优化问题[33-35]，从而计算出原方程组的数值解。文献[33]采用自适应粒子群算法对一次侧的电感和电容参数进行辨识，该方法辨识准确率高并且具有一定的创新性，但文献没有提到对4个参数的同时辨识。文献[34-35]分别使用了混沌优化算法和遗传算法来求方程的数值解。然而，上述智能优化算法的参数辨识结果往往会因为初始值不合适而陷入局部最优。且对于多参数辨识模型，基于标准优化算法的参数辨识精度不高。除此之外，传统的智能优化算法无法解决系统多解问题。

还有一些研究采用解析和数值方法相结合的方式来辨识系统的参数[36]，文献[37]采用解析法计算电感值，采用进化算法确定WPT系统建模所需的其他参数值。

针对上述问题和以上研究，本文提出了一种基于迭代循环的粒子群算法对WPT系统中的多个参数进行辨识，充分考虑了互感不确定、谐振系统多个电路参数同时发生偏移等复杂情况，在检测量较少的条件下能达到很高的辨识准确率。该方法根据谐振电路模型建立与待辨识参数有关的电路方程，并以检测量的理论值与实际值之差的绝对值来构造最小化目标函数，利用设计好的优化算法进行循环迭代不断使待辨识参数接近真实值。通过仿真和实验验证该方法的有效性，辨识准确率可达到95%左右。

1 谐振式无线充电系统的数学模型

1.1 串联谐振电路拓扑结构分析

磁耦合谐振式无线充电技术能很好地满足电动汽车充电效率要求，也能够全面考虑充电距离和抗外界干扰等因素。基本的磁耦合谐振式无线充电系统结构一般包括一次侧电力变换单元、二次侧电力变换单元和谐振补偿电路。谐振补偿电路是无线充电系统中重要的部分，本文研究的是串联-串联（Series-Series, SS）谐振补偿电路，结构如图1所示。

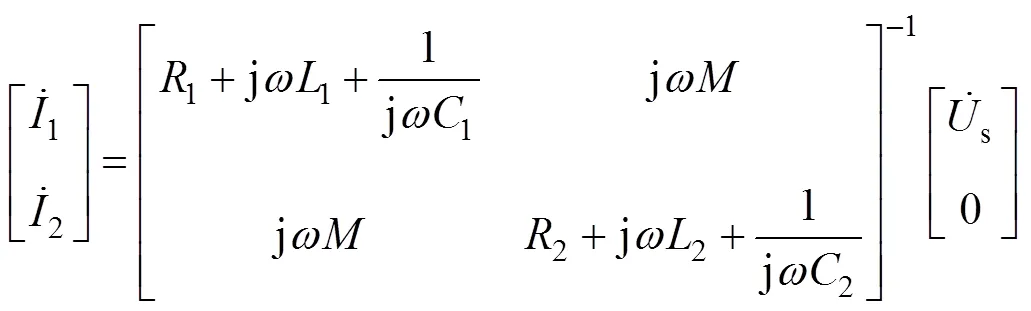
电路一次侧和二次侧的等效阻抗分别为

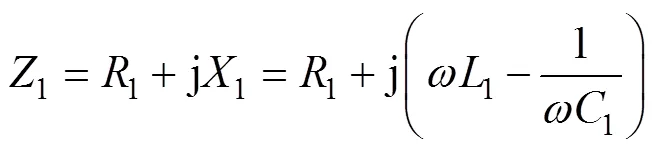
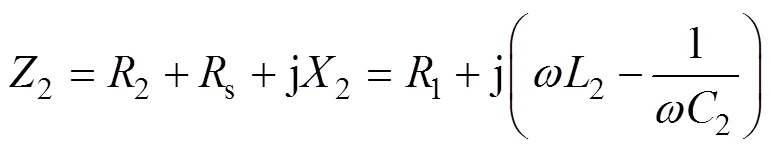
根据式（1）～式（3），可以得出

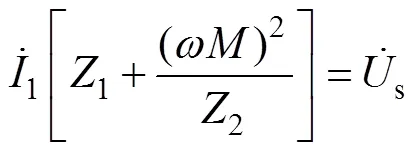
通过将谐振电路的二次侧阻抗折算到一次侧，等效电路如图2所示。

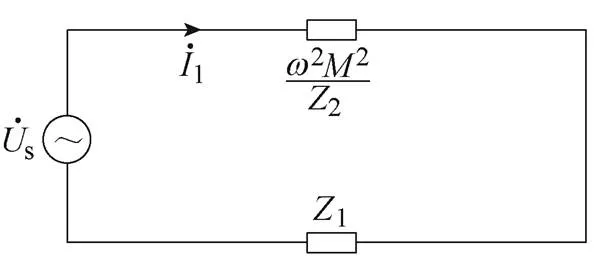
图2 谐振电路中二次侧阻抗折算到一次侧等效电路

由图2可知，转换后的等效阻抗可表示为

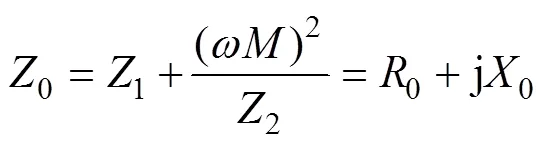
其中

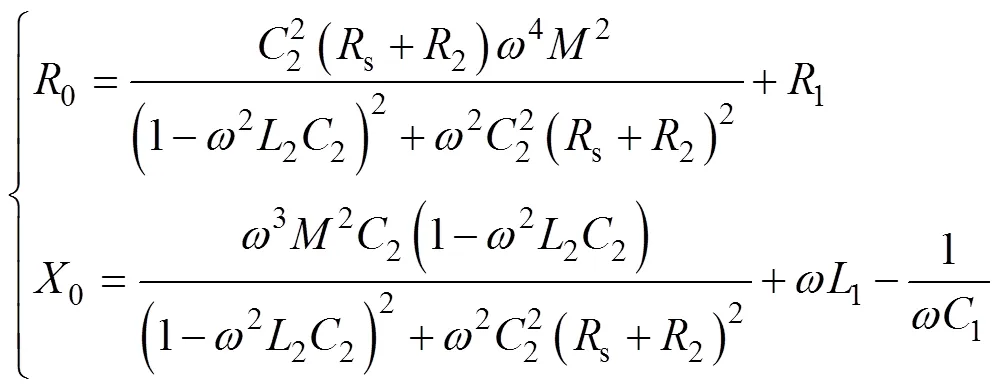
谐振电路一次电流的相量表达式为

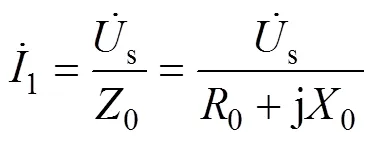
为了便于具体计算，将上述的一次电流相量表达式转换为标量，表示为

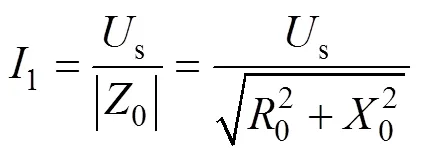
同样地，将二次电流相量表达式转换为标量表示为

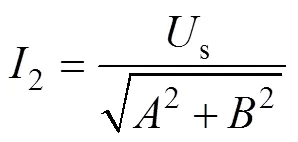
其中

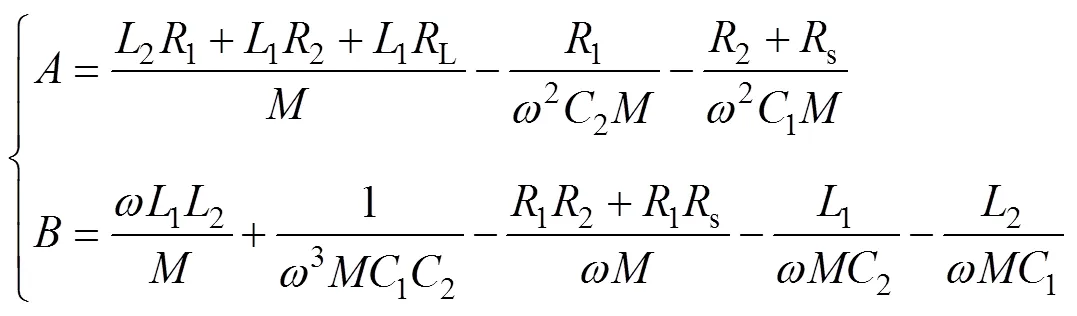
式中，为互感；L为负载。

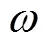
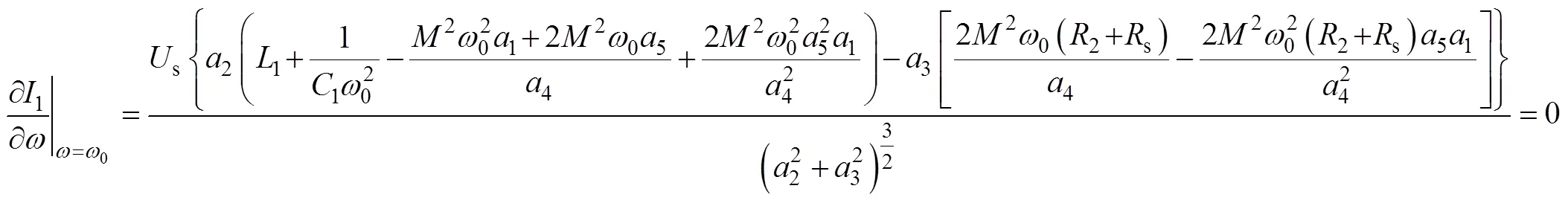
将式（11）进行等效变换得到

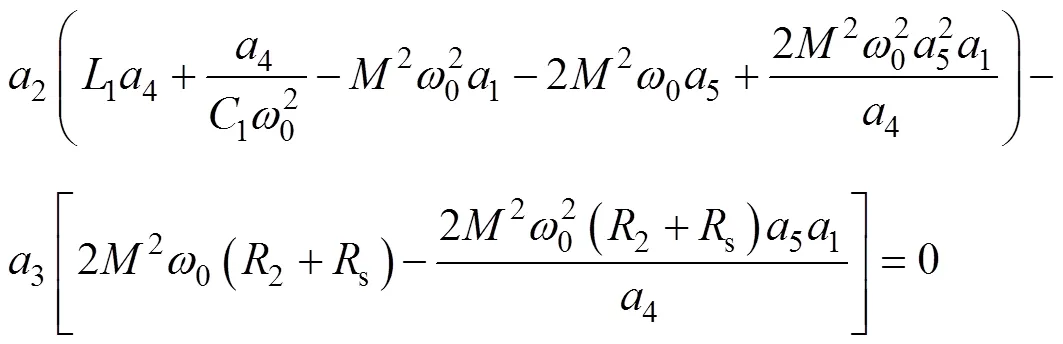
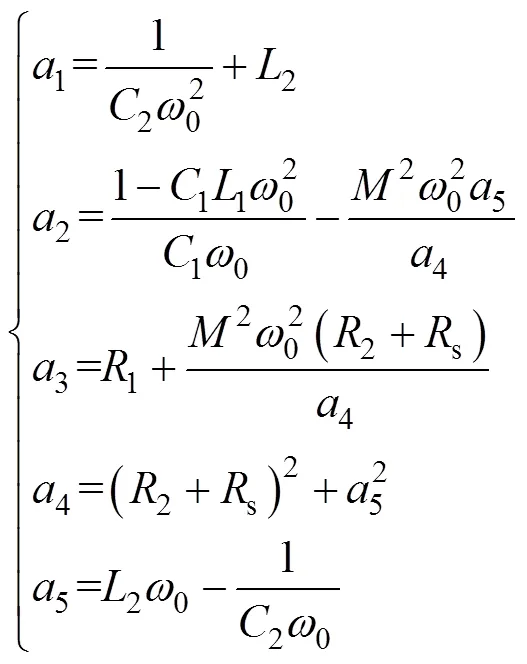
将式（14）等效变换为

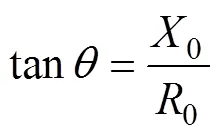
1.2 特征量的提取

2 参数辨识问题分析

根据第1节建立的无线充电系统模型，最终需要研究的4个非线性方程组为式（8）、式（9）、式（12）和式（15）。对于特定的某一个系统，只要测量出第1节提到的特征量，式（8）、式（9）、式（12）和式（15）就成为只含有1、1、2、24个电路参数的方程，将4个方程整理成方程组为

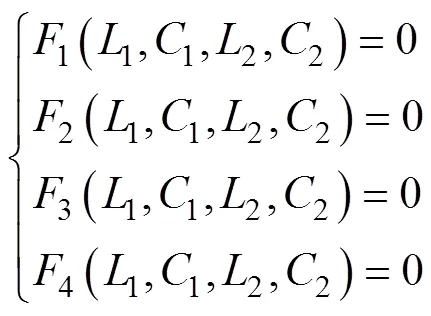
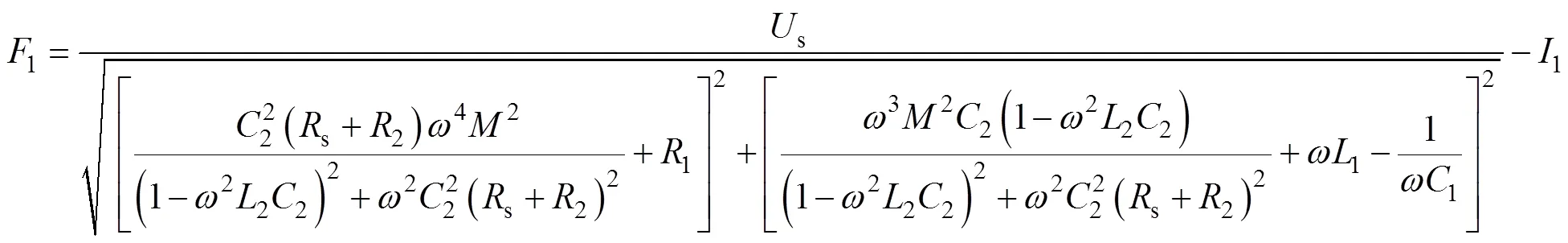
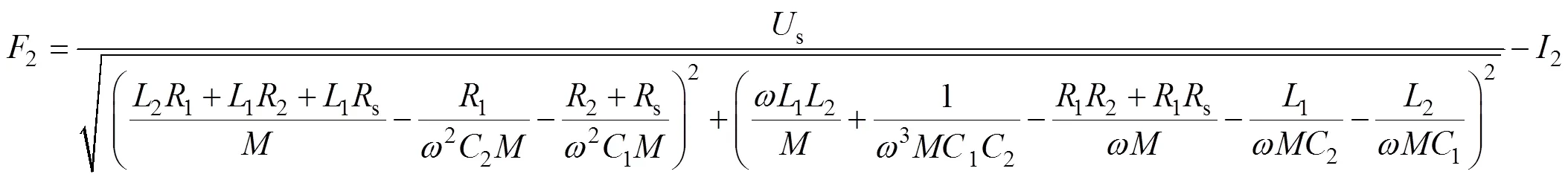
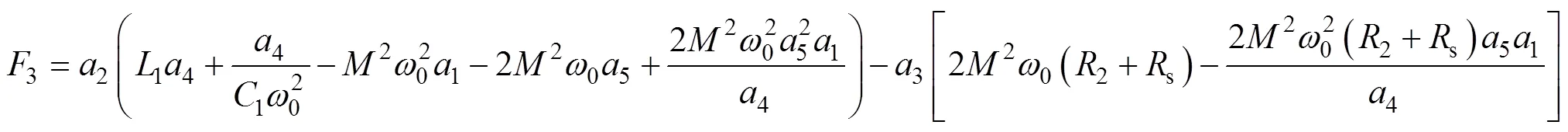
理论上，只需要解出由上述4个方程构成的方程组就可以得到谐振电路的4个电路参数。但是由于系统模型的4个方程均为高阶非线性方程，很难甚至无法求出其解析解。同时，该非线性方程组存在有多解的可能，只有一组解是4个参数的真实值，这组解为期望解，其余解为非期望解。求非线性方程组数值解传统的方法是牛顿迭代法，但是该方法存在计算量大、对初值选取要求高等局限性。以上情况给电路参数的辨识带来了很大困难，本文考虑将多元方程组的求解问题转化为函数的优化问题，使用改进的优化算法来寻找最优解作为原方程组的近似解。

3 基于标准粒子群算法的参数辨识

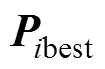
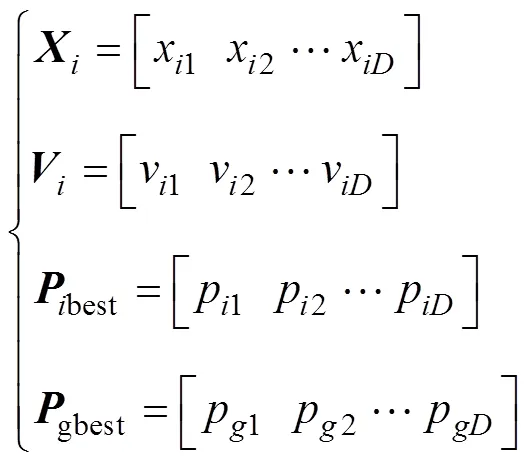
粒子的位置与速度更新规则为

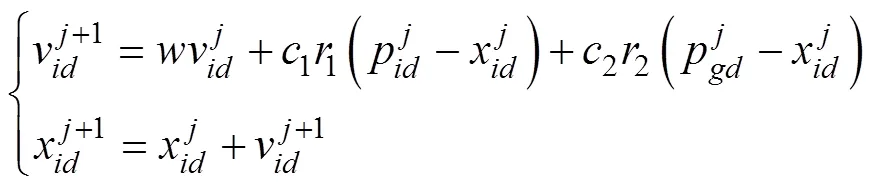
根据方程组式（16）构造了适应度函数为

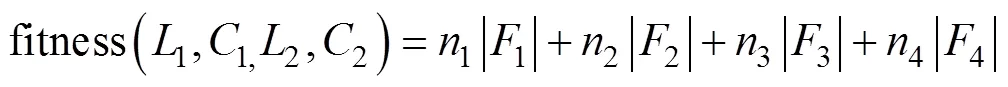
式中，n（=1, 2, 3, 4）为惩罚系数。PSO算法的优化目标是寻找出使适应度函数值达到最小的1、1、2和2。此时辨识出的参数是最接近真实值的。下面给出几组不同条件下基于标准粒子群算法的WPT系统的电路参数辨识结果：

算例1：1、1、2和2参数初始设计值分别为280mH、13nF、127mH和28.5nF，为了模拟实际系统中参数漂移的情况，在仿真平台上设置1、1、2和24个参数的真实值分别为250mH、18nF、140mH和26.7nF。4个参数偏移百分比分别约为10.7%、38.5%、10.2%和6.3%。辨识结果见表1。

从表1可以看出，采用标准PSO算法直接辨识4个参数得到的辨识结果精度较低，其中1的误差将近20%。其算法迭代如图3所示，在800代左右函数适应度值不再下降，但4个参数辨识值与真实值相差较多，表明基本PSO算法已经陷入局部最优。

表1 算例1中基本粒子群优化算法辨识结果

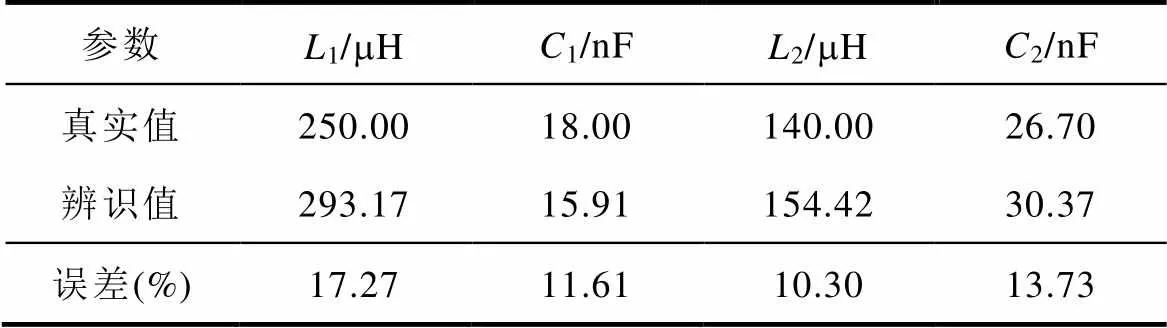
Tab.1 Identification results based on standard PSO algorithm in Case 1

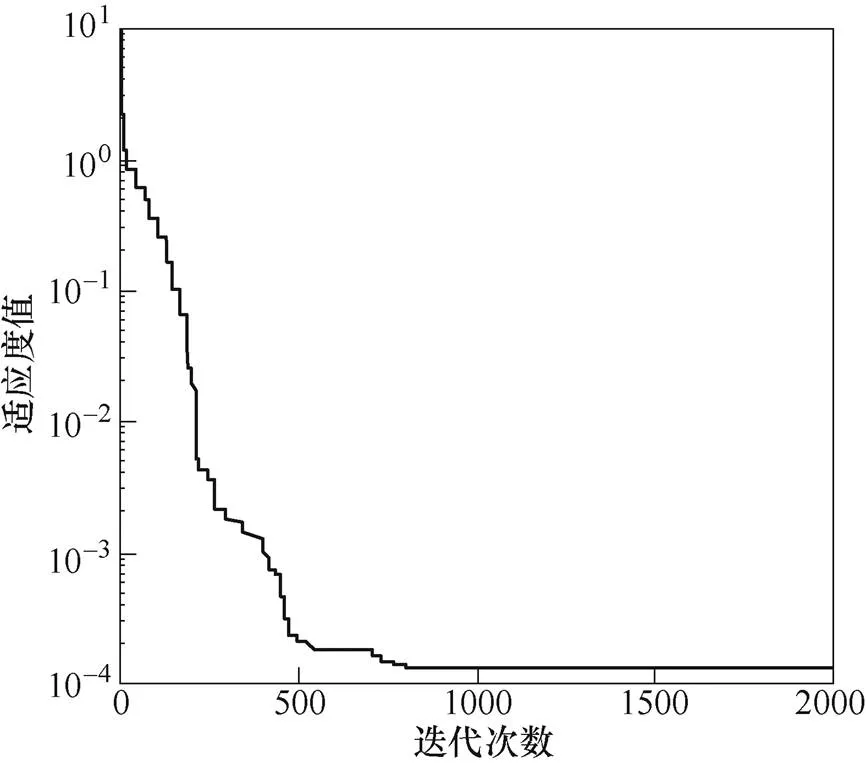
图3 算例1中基本粒子群算法迭代

算例2：1、1、2和2参数初始设计值分别为290mH、12nF、132mH和17.2nF，在仿真平台上设置1、1、2和24个参数的真实值分别为270mH、15nF、145mH和25.5nF。参数辨识结果见表2。

表2 算例2中基本粒子群优化算法辨识结果

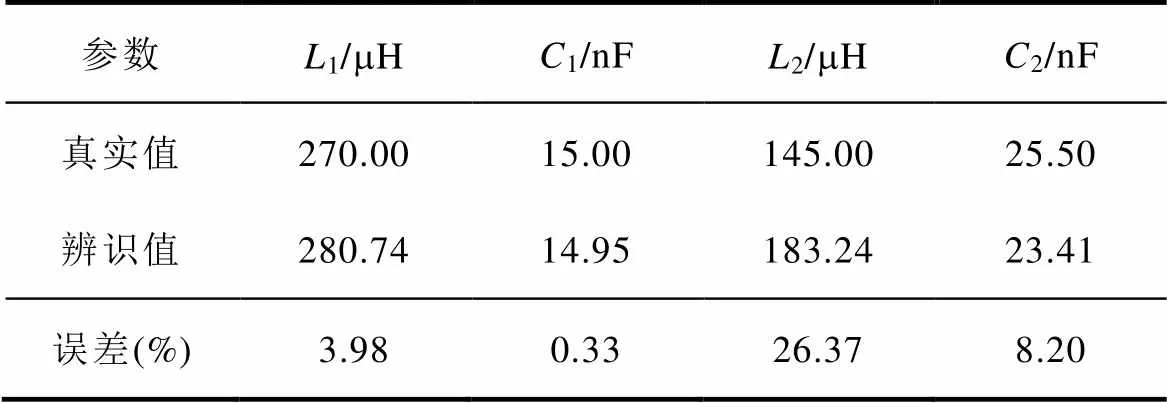
Tab.2 Identification results based on standard PSO algorithm in Case 2

（1）当使用标准的PSO算法直接同时辨识4个参数，由于函数结构复杂、非线性程度强、变量个数较多，极易陷入局部最优。

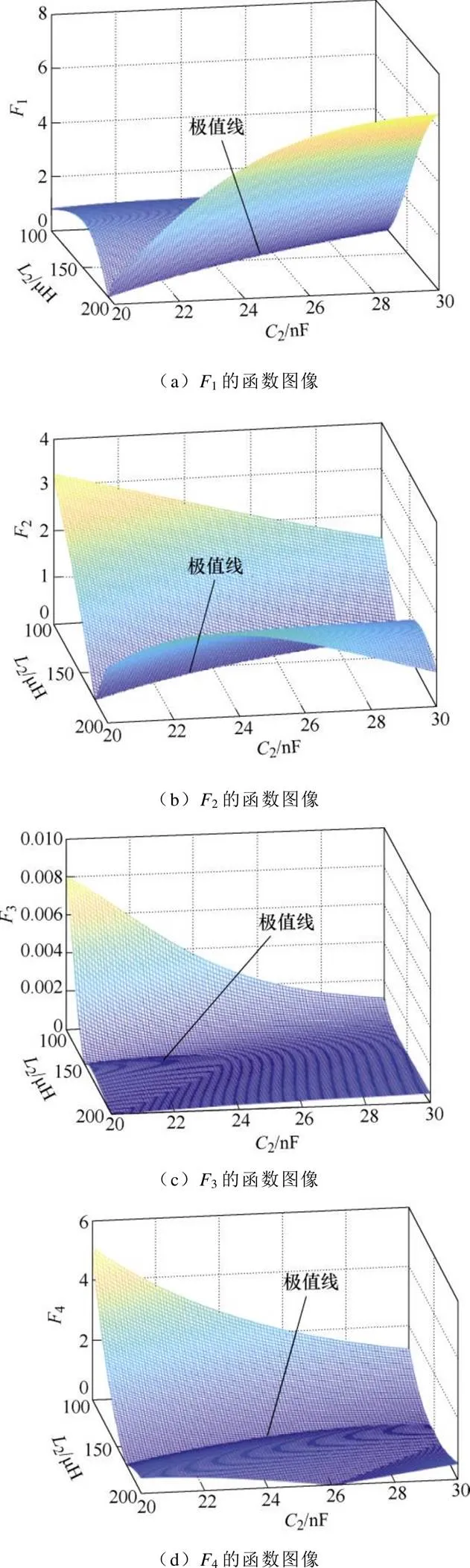
图4 在L1=270mH, C1=15nF条件下F1～F4的函数图像

（2）系统存在有多解的情况且无法保证辨识结果为期望解。

4 参数辨识方法的改进

为了解决上述问题，本文提出了一种基于循环迭代粒子群优化（Loop-Iteration Particle Swarm Optimization, LIPSO）算法来对WPT系统的参数进行辨识的方案。为了方便表达，1和1定义为第一组参数，2和2定义为第二组参数。每一次先只辨识一组参数（第一组或第二组），然后使用上一步辨识出的结果作为初始条件循环辨识另一组参数。让辨识的结果不断接近并收敛于方程组式（16）的解。并且在使用PSO算法时通过找出合理的约束条件来减小非期望解出现的概率，最后根据第一组和第二组参数之间的灵敏度关系来调整适应度函数中每一项的惩罚系数。循环迭代粒子群算法对WPT系统的参数辨识过程如图5所示。

4.1 基于循环迭代粒子群算法的参数辨识

该参数辨识的方案是分步进行的，多轮辨识的过程，步骤如下：

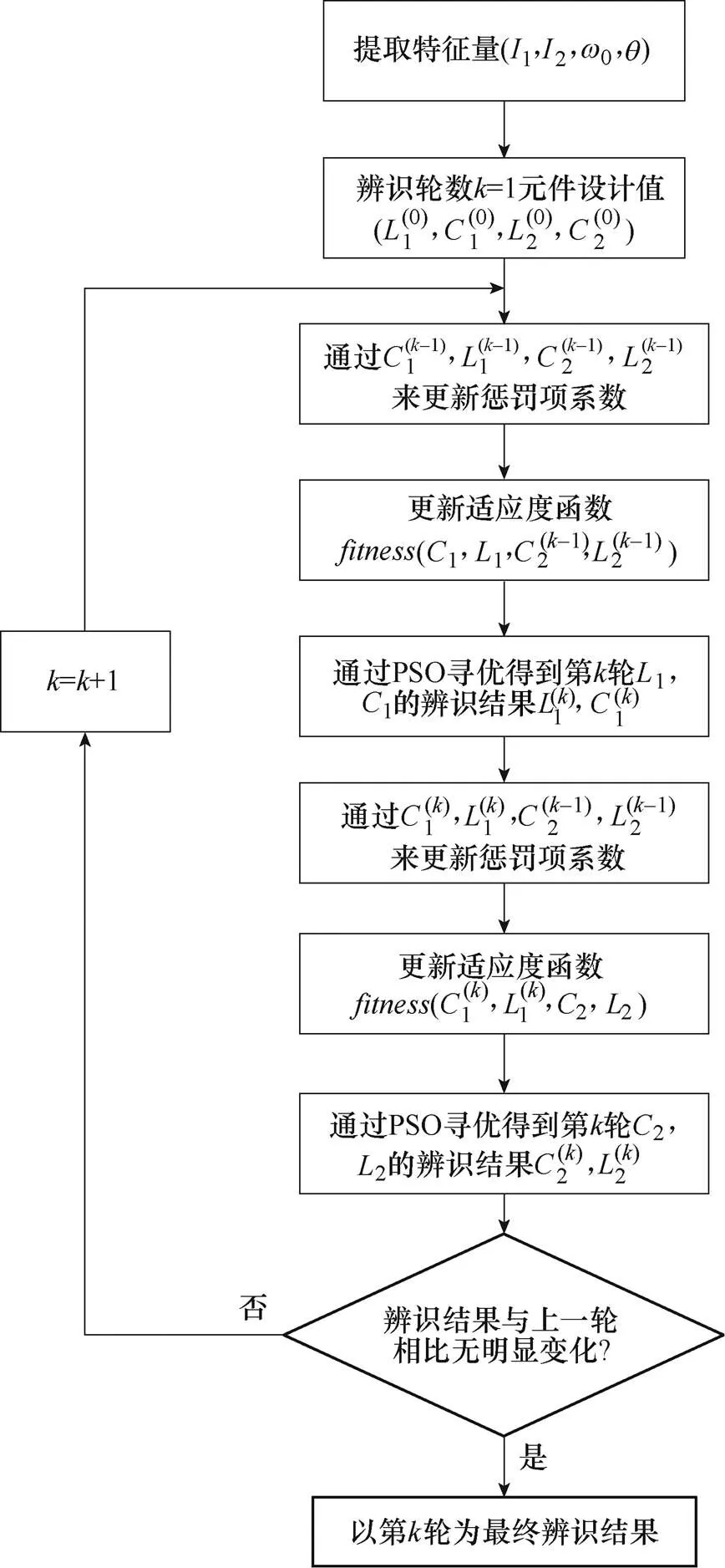
图5 基于循环迭代粒子群优化算法参数辨识过程流程

4.2 寻优过程约束条件的选取

通过上述方法可以避免在寻优过程中出现局部最优的情况，从而使辨识结果收敛到原方程组的一组解，但是这组解仍然可能是一组非期望解。为了解决这一问题，还需要额外增加一个约束条件来对辨识结果进行限制。考虑到用于寻优的适应度函数是由四部分组成，每一项都是代表一个方程的函数。使用PSO算法的寻优就是不断更新迭代来寻找同时满足这4个方程的解的过程。当这4个函数零点附近极值线的走向趋于一致甚至部分重合时就会出现多个满足方程的公共解，如图4所示。因此在寻优过程中考虑使用一个有效的约束函数，这个函数的极值线与前面4个函数的极值线有明显不同的走向并且与它们有较大的相交角度而不是大致重合，以此来排除掉大量的非期望解。通过多次比较与分析，利用二次侧的特征频率构建一个极值约束方程是能达到此效果的。构造的约束方程如式（24）所示。该式不参与目标函数的构建，而是作为一个约束函数对辨识结果进行筛选，如果辨识结果不满足约束方程，则需要再次进行辨识，直到满足为止。

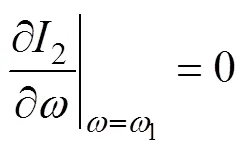
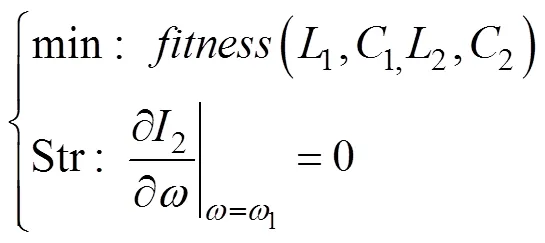
4.3 惩罚系数的自适应调整

本文对适应度函数里面的惩罚系数进行了相应研究并作出改进，先考虑以下问题，只有两个未知数的情况下有系统方程和目标函数分别为

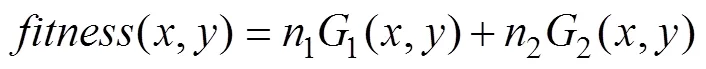
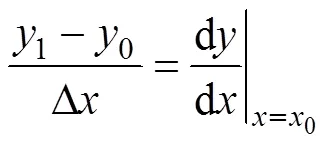
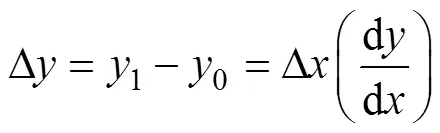
在本方案中，适应度函数中每一项的惩罚系数都会根据两组参数之间灵敏度进行自适应调整。每一次的辨识都会有一次适应度函数的迭代更新，为了使结果更加合理，应该保证让适应度函数里面的每一项都在同一数量级而不能相差过大；第一组参数与第二组参数之间的敏感程度也会影响辨识的准确率，因为每一次的辨识都是以上一次已经辨识出来的一组参数作为已知量，去辨识剩下的两个参数。若第一组（第二组）参数对于第二组（第一组）参数敏感性太强，即使已辨识出的一组参数已经比较准确，也会使待辨识的另外一组参数产生较大误差。

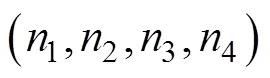
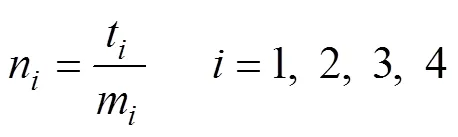
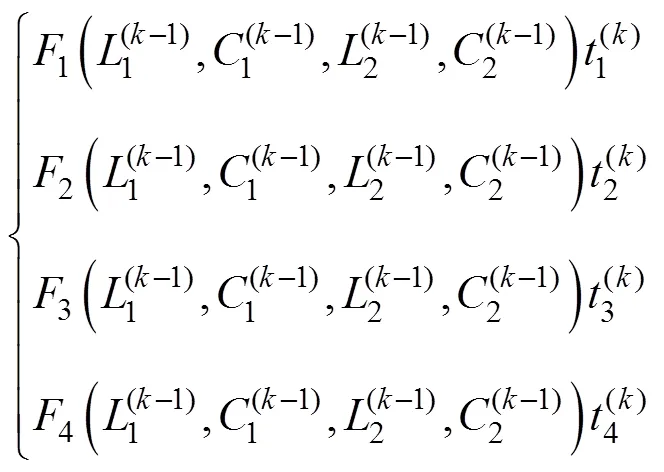
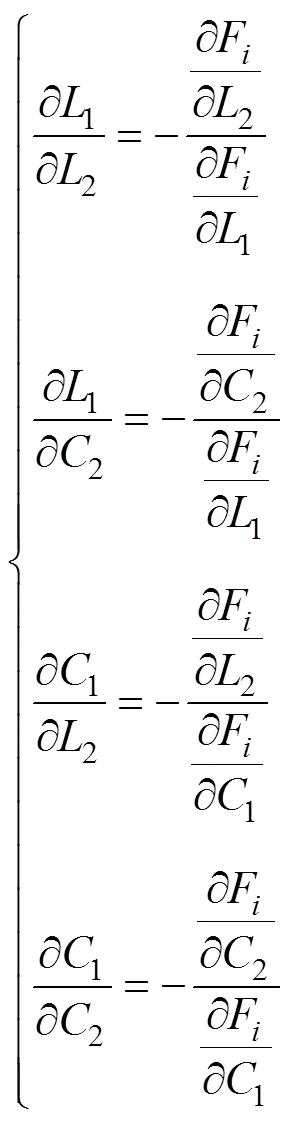
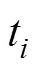
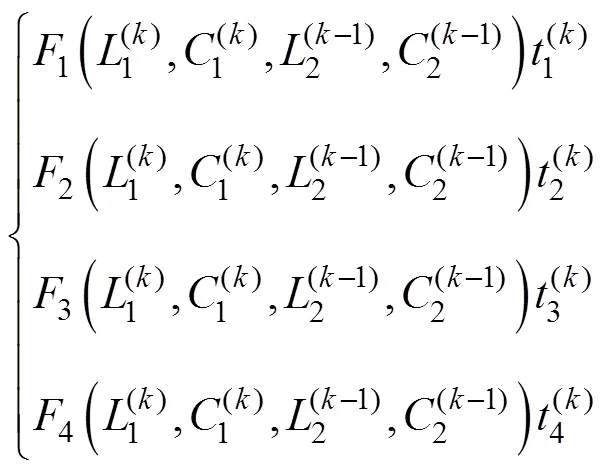
式中，所有参数的数量级相同。

基于标准PSO算法的辨识方法是一个随机搜索的过程，每次辨识的结果可能都不一样，无法确定哪一次的结果是更优的，而改进后的辨识方案的搜索过程更具有“目的性”，每一轮的循环迭代都会往真实值靠近。由于参数的设计值与真实值之间存在不同程度的偏移，第一轮辨识出来的结果一般误差会较大，随着迭代循环次数的增加，总体上辨识结果会不断接近并收敛于真实值。电子元件参数漂移往往是一个长期缓慢的过程，在一次实验辨识过程中可以认为电路参数值是不发生改变的，因此可以保证通过该方案辨识出的电路参数是合理有效且具有实时性的。

5 仿真和实验验证

5.1 仿真结果与分析

算例3：为了验证第4节提出的识别方法的有效性，在与第3节的算例1相同的条件下，基于改进的循环迭代PSO算法再次辨识了4个电路参数。并与算例1的辨识结果进行了对比。两种辨识方法中仿真系统的主要参数见表3。

通过仿真得到算例3中的一次电流波形如图6所示。从电流波形中提取的一次侧稳态电流的有效值约为1.236 8A。

表3 算例3中仿真平台的主要参数

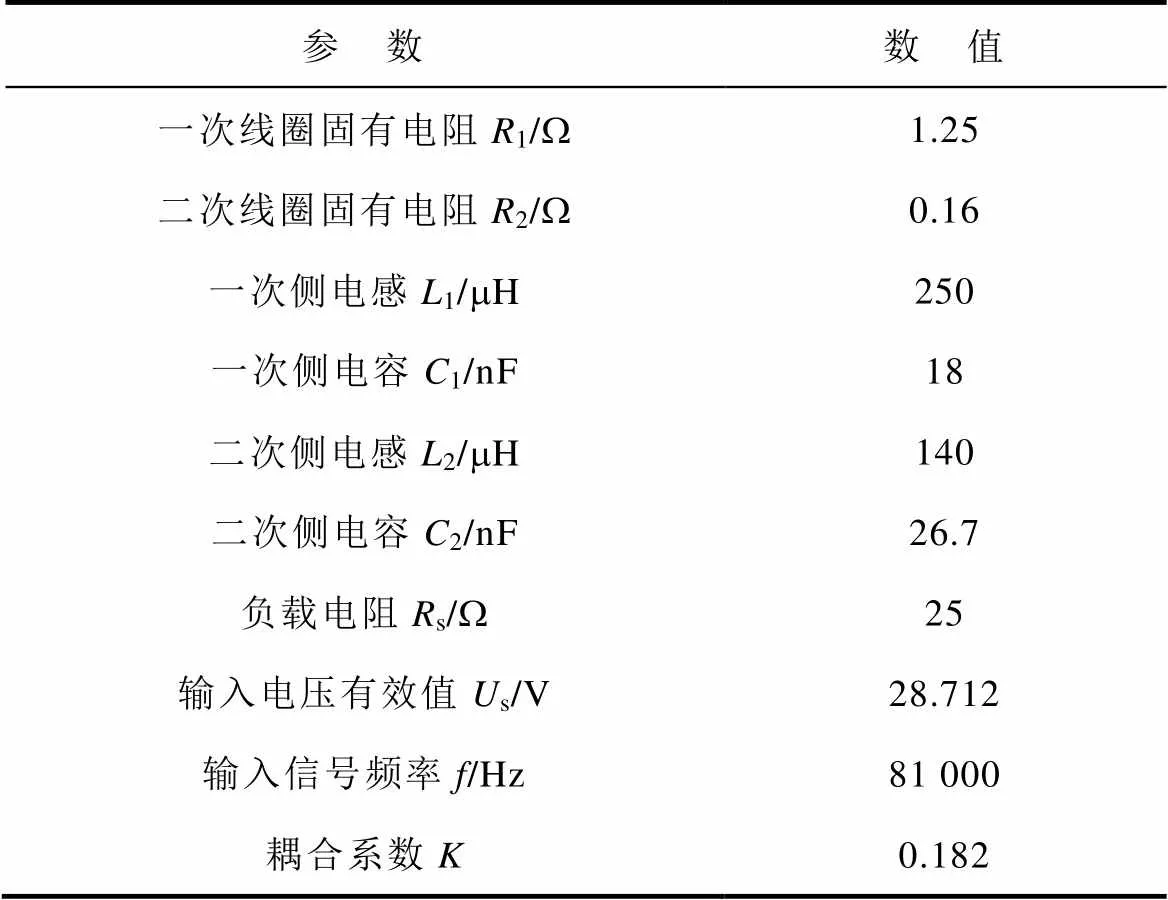
Tab.3 The main parameters of the simulation system in Case 3

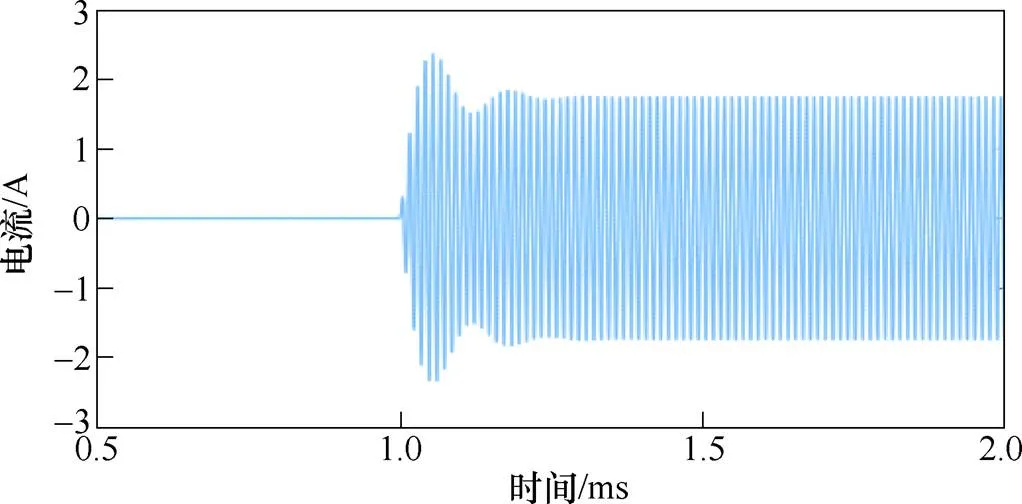
图6 算例3中一次电流波形

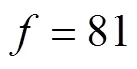
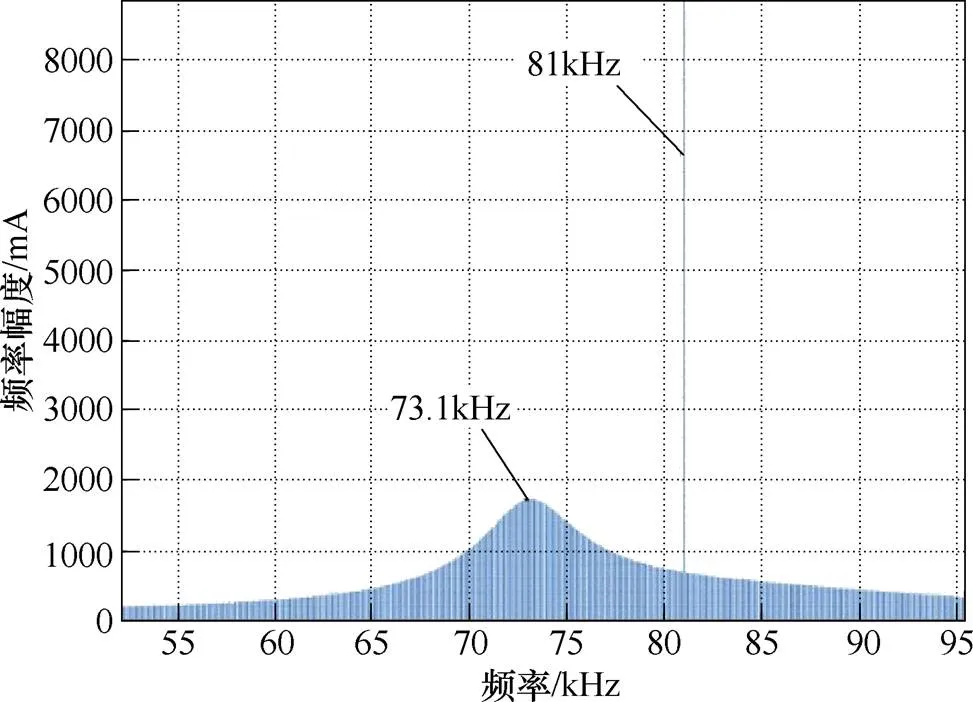
图7 算例3中一次电流的傅里叶频谱

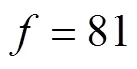
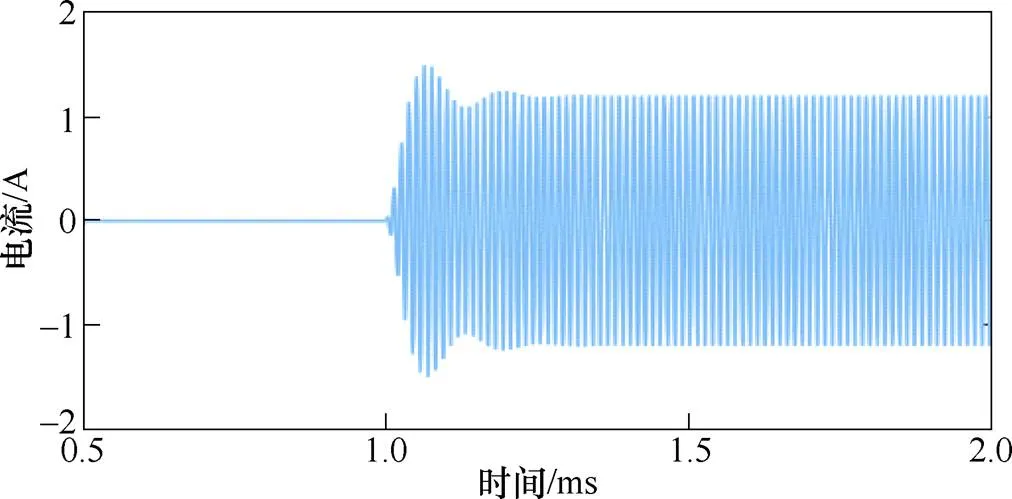
图8 算例3中二次电流波形

基于循环迭代粒子群算法的辨识结果见表4。

由表4可以看出，4个参数的识别精度均达到99%以上。与第一轮和第二轮相比，第三轮的辨识结果具有更高的精度。为了避免实验偶然性，在不同工况下进行多次实验，发现均可以达到较高的精度。因此可以认为，随着辨识轮数的增加，辨识值更接近实际值，并收敛于实际值。两种方法的误差见表5。从表4和表5可以看出，与标准PSO算法相比，本文提出的改进方案具有更高的识别精度和更小的识别误差。结果表明，改进后的方法能较好地解决局部最优问题。

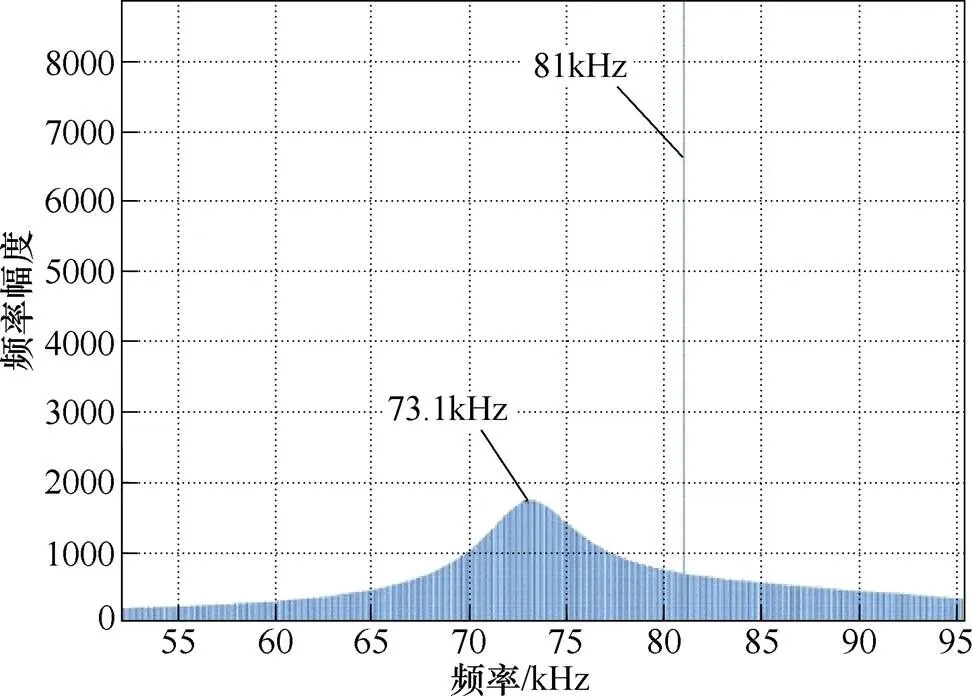
图9 算例3中二次电流的傅里叶频谱

表4 算例3基于循环迭代粒子群算法的辨识结果

Tab.4 Identification results of parameters based on LIPSO in Case 3

表5 标准粒子群算法在算例1和循环迭代粒子群算法在算例3中的辨识误差

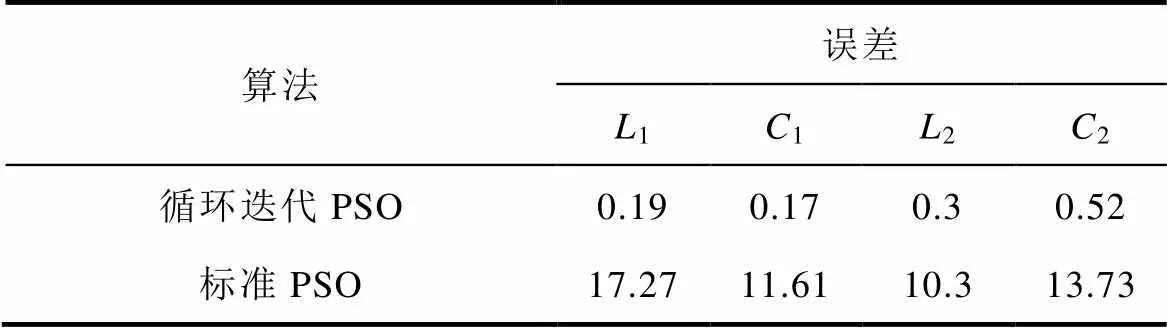
Tab.5 Identification error of standard PSO in Case 1 and LIPSO in Case 3 （%）

算例4：为了对寻优过程中添加的约束条件的有效性进行验证，在第3节算例2相同的条件下，进行了两种不同方式的辨识：使用循环迭代PSO算法并且添加约束条件式（24）；仅使用循环迭代PSO算法但没有添加约束条件。并将辨识结果与第3节算例2的辨识结果进行比较。

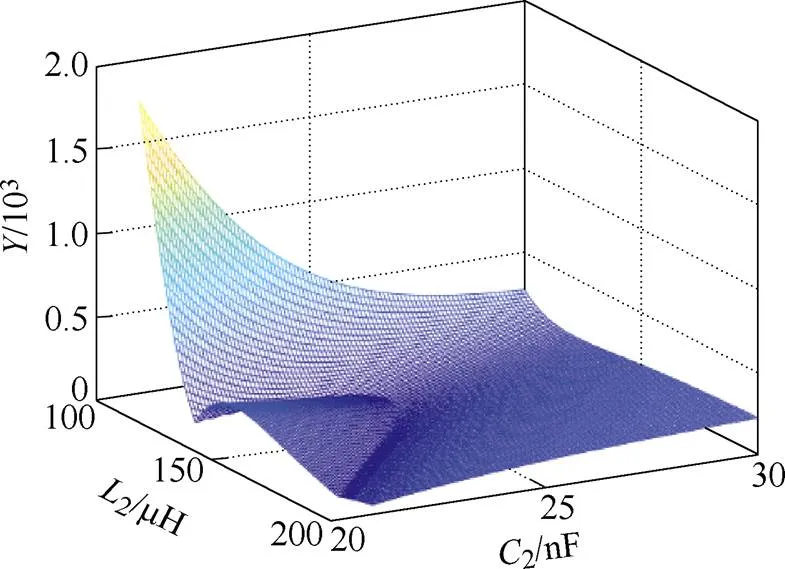
图10 在L1=270mH，C1=15nF的条件下约束函数的图像

带约束方程和不带约束方程的LIPSO参数辨识结果分别见表6和表7。

从表6和表7可以看出，通过添加约束方程，参数辨识的结果已经趋近于实际值，且辨识精度较高。由表7可以看出，如果不添加约束方程，在三轮辨识过程中，寻优时总是落入一个相差较大的非期望解。表8中列出了三种方法的识别误差（标准PSO、带约束方程的LIPSO、不带约束方程的LIPSO）。

表6 算例4中带约束方程的循环迭代粒子群算法的参数辨识结果

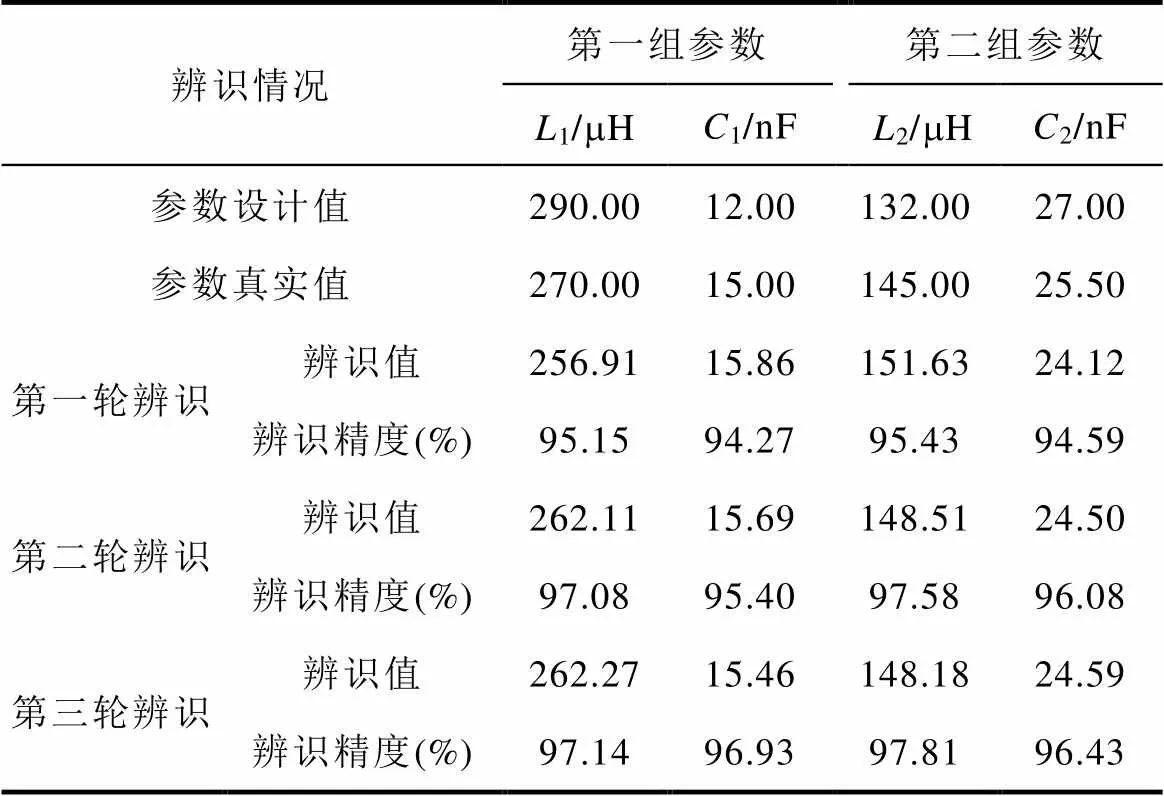
Tab.6 Parameter identification results of LIPSO with constraint equation in Case 4

表7 算例4中不带约束方程的循环迭代粒子群算法的参数辨识结果

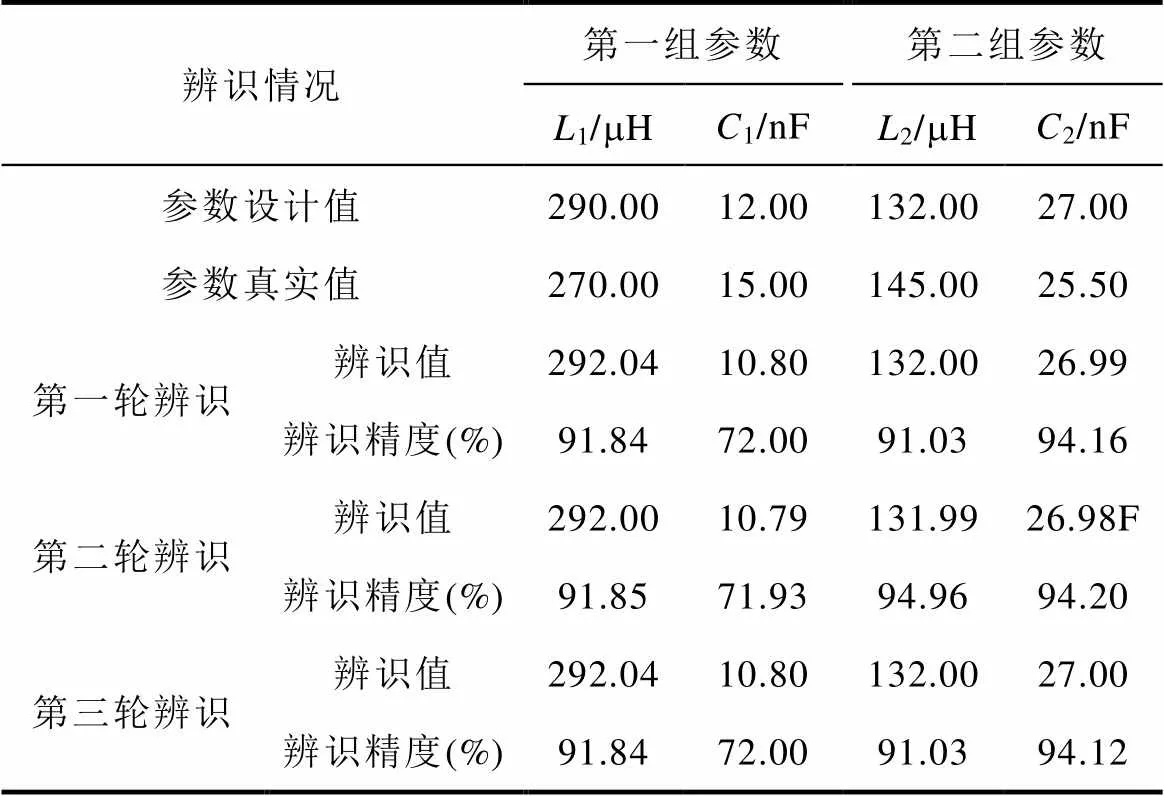
Tab.7 Parameter identification results of LIPSO without constraint equation in Case 4

表8 标准粒子群算法和循环迭代粒子群算法（带约束和不带约束）的辨识误差

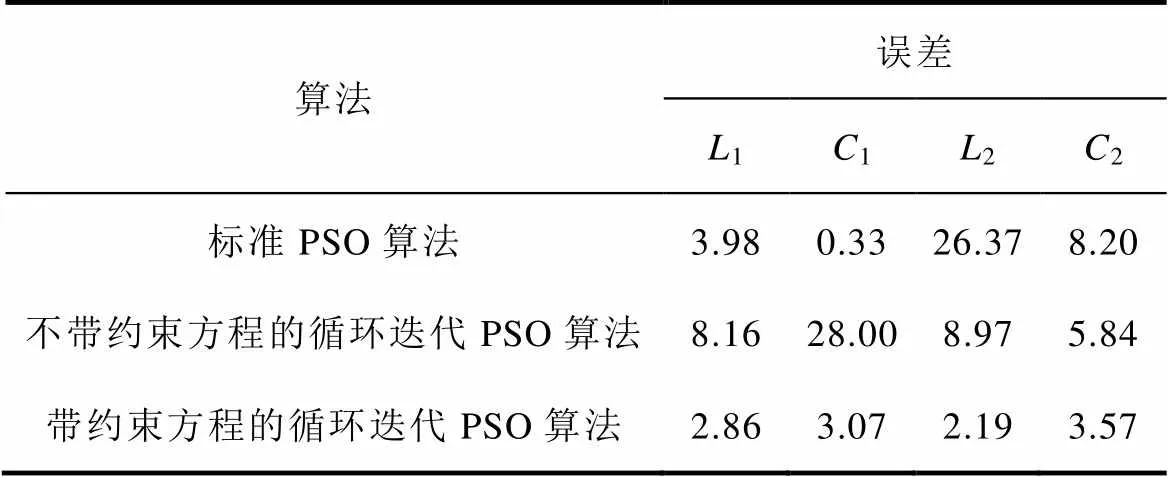
Tab.8 The identification errors of standard PSO and LIPSO (with and without constraint equation)（%）

从表8中不难看出，使用标准粒子群算法的2辨识效果很差，误差达到26.37%，基于无约束方程的循环迭代粒子群算法1的辨识效果也很差，误差为28%。与上述两种方法相比，带有约束方程的循环迭代粒子群算法对4个参数中任意一个参数的辨识误差都是最小的。从以上结果的分析来看，由于式（24）的约束，可以有效避免非期望解。

5.2 实验结果与分析

为了进一步验证该方法的可靠性，本文在一个功率可达200W，充电频率为81kHz的实验平台进行了实验。实验平台如图11所示。图11a中，线圈绕线由多股利兹线组成，以中心为起始点，紧挨向外排绕，形成圆盘形，线圈直径约为50cm。一次与二次线圈均有头、中心、尾部三根引线，其中一次线圈头-尾匝数为500匝，中心-尾部匝数为250匝；二次线圈头-尾匝数为280匝，中心-尾部匝数为140匝。图11b则为模拟电动汽车真实充电情况下线圈摆放位置。上方线圈为电动汽车放置于底盘的二次线圈，下方线圈则为放置于地表面的一次线圈。两线圈处于正对位置，且间距大约在15cm。

图11 WPT系统的实验平台

由于实验室条件的限制，实验平台的参数与仿真平台的参数不一致。实验平台的主要参数见表9。

基于实验平台检测出5个特征量。利用高速采样板卡采集了实验平台的电路信息并在上位机中进行了特征量提取。具体计算方法如下：

表9 实验平台的主要参数

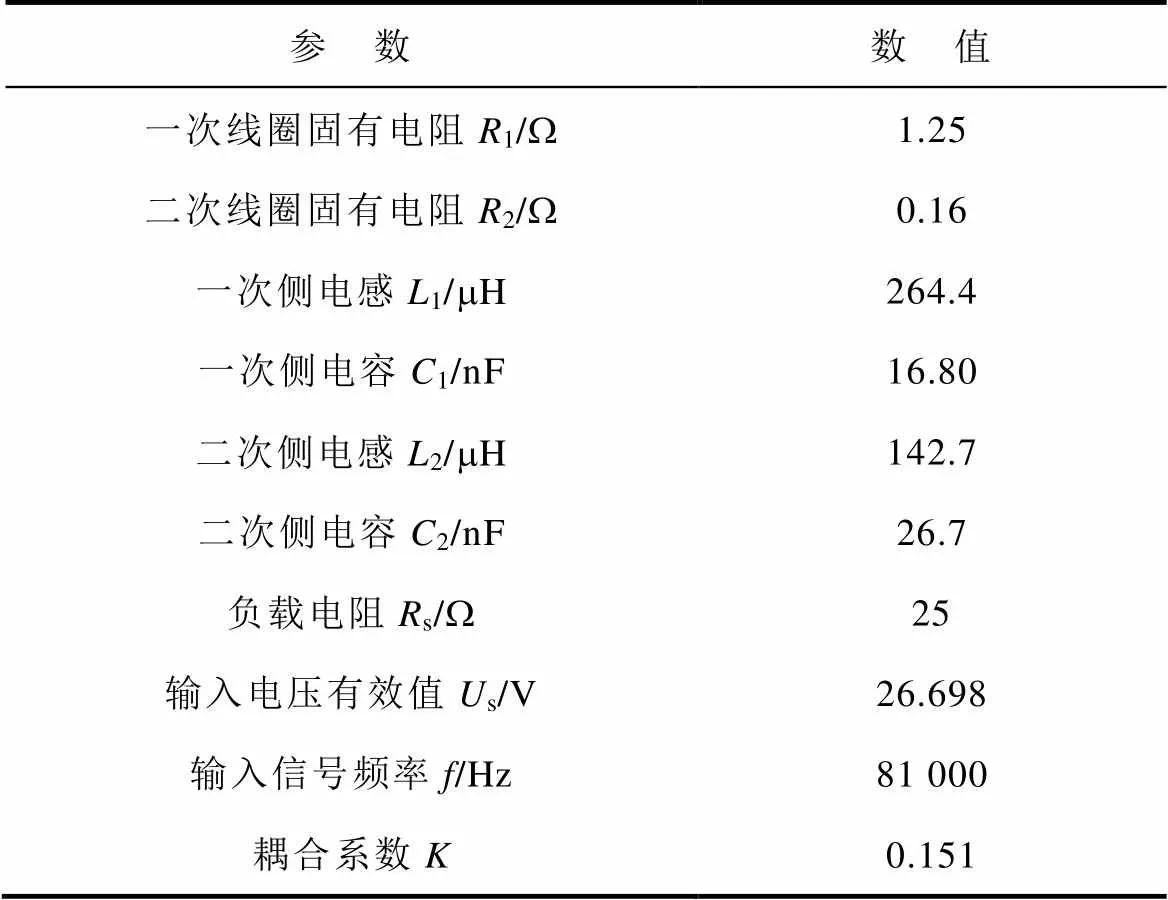
Tab.9 The main parameters of experimental platform

电流、电压有效值的提取：PCI-1714U板卡一共有4个通道，其中3个通道分别采集一次电压、一次电流、二次电流，第4个通道作为信号触发通道。本文采用方均根的方式计算电压与电流的有效值，电压、一次电流与二次电流的计算公式分别为

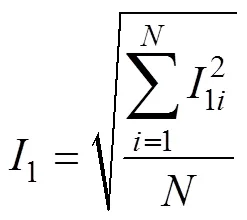
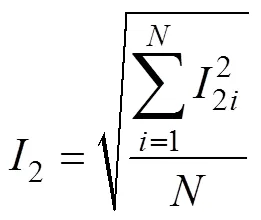
特征频率值的提取：通过傅里叶变换可以将采集到的时域上的电信号转换成频域信息。由于每个通道采集个点，通过快速傅里叶变换转换为频域上的个点。除去第一个点（直流分量），剩下的点频谱幅值与原电信号的幅值成正比。从第4节的傅里叶频谱分析可以看出，特征频率点是一个局部极大值点，对应的幅值大小仅次于输入频率对应的点。因此，只需要在剩下的点中找到幅值第二大的点对应的频率即为特征频率。通过快速傅里叶变换转换后的点是复数形式，只需要算出复数的模就能计算出频域上每个点的幅值。在个点中遍历即可找出第二大幅值对应的点0。

假设采样频率为s，进行傅里叶变换之后，某一点n（=1, 2, 3,…,）的频率可表示为

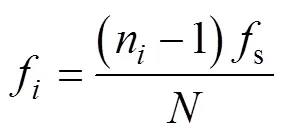
因此特征频率0为

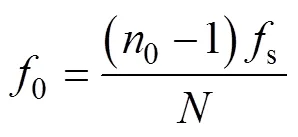
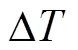
图12 过零检测计算相位差原理示意图

提取得到一次电流和二次电流有效值分别为1.41A和0.81A。一次电流和二次电流的特征频率分别为74.2kHz和74.3kHz。电压和电流的相位差为1.82。特征量检测波形如图13所示。

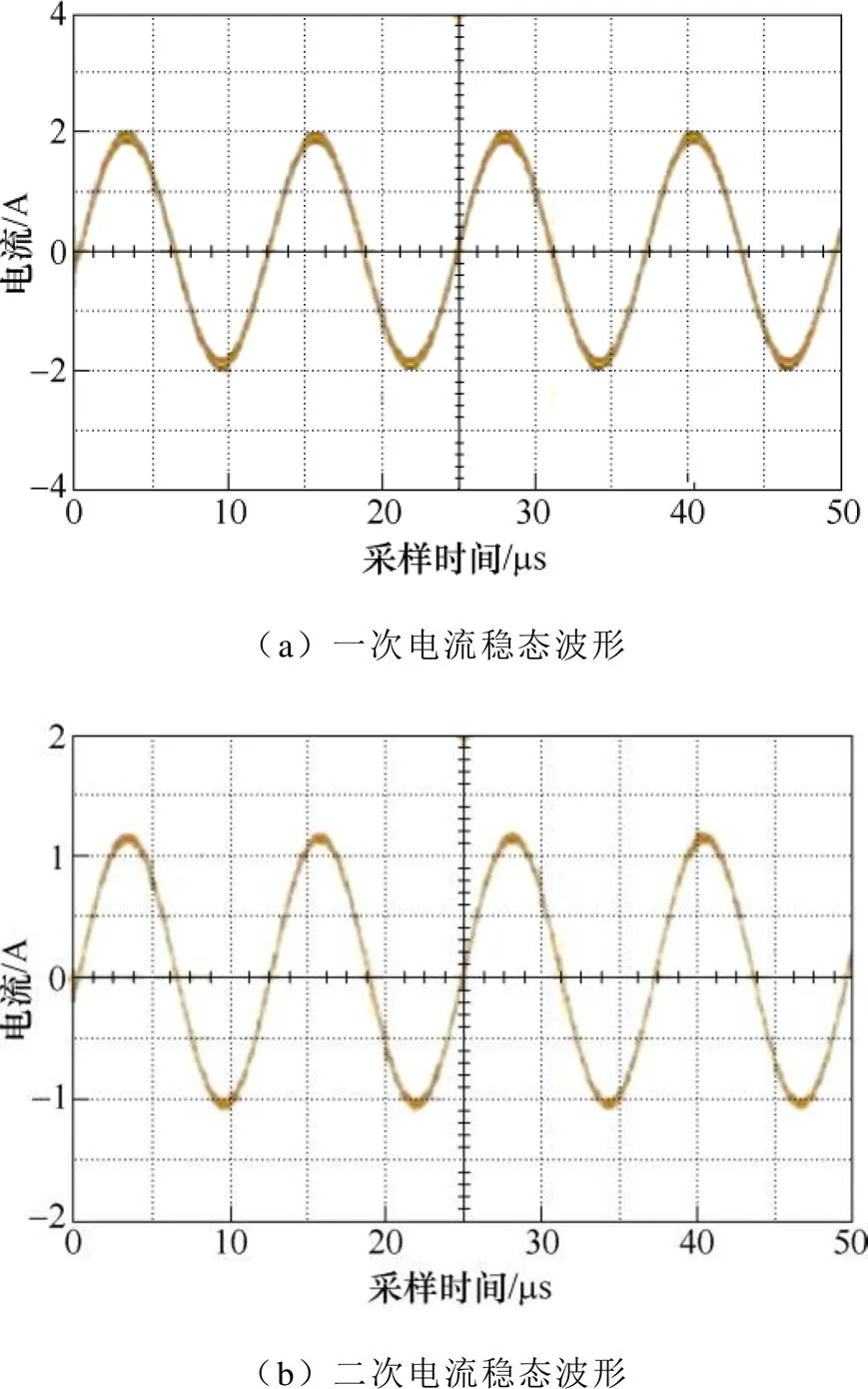
图13 基于实验平台的检测量波形

将特征量的值代入含有4个待辨识参数的模型中，并利用循环迭代PSO算法对电路参数进行辨识。基于循环迭代PSO算法的辨识结果见表10，经过三轮辨识，辨识结果已经收敛。可以看出4个

参数中1、1的辨识精度很高（分别为99.56%和98.99%），而2、2的辨识精度略低（分别为94.68%和95.81%）。经过多次对比实验发现，在相同条件下，基于实验平台的参数辨识精度略低于仿真平台的参数辨识精度。主要原因是在实验平台上，提取的检测量会有一定的测量误差。一系列实验结果表明，所提出的参数辨识方案是合理可行的。

表10 实验平台下参数的辨识结果

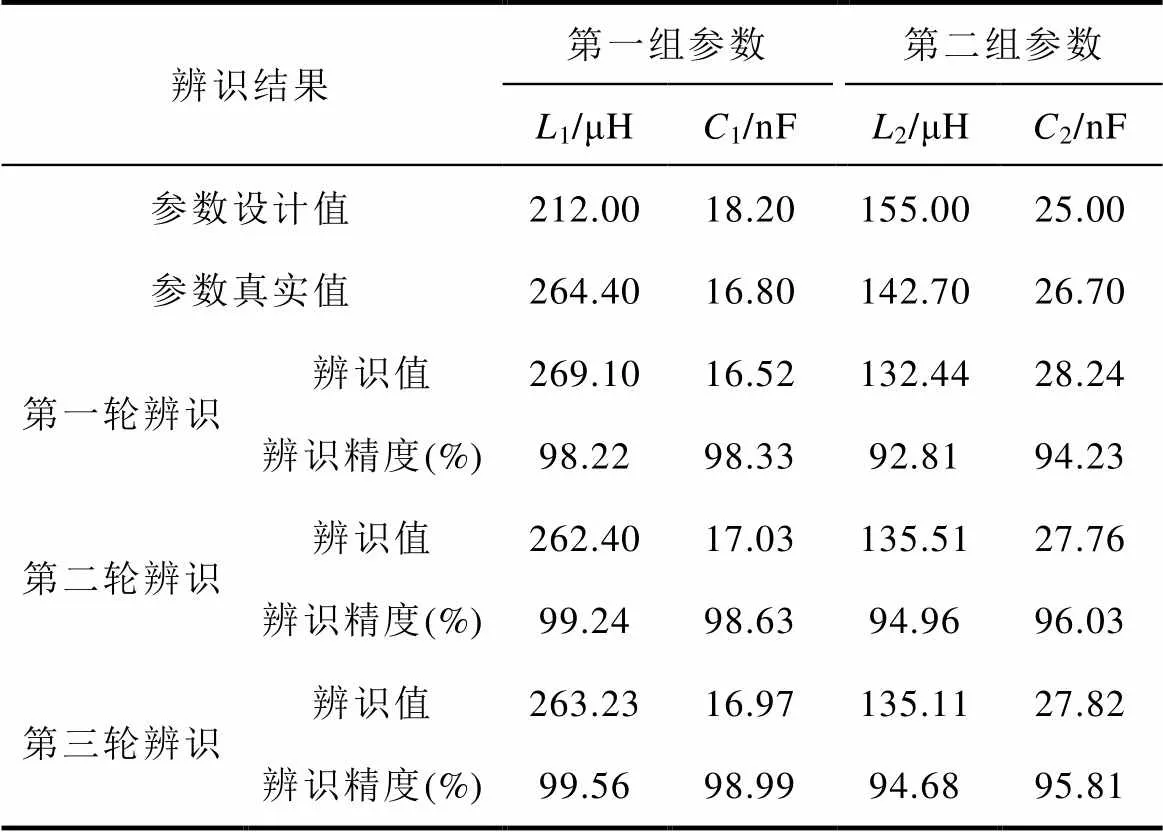
Tab.10 Parameter identification results on the experimental platform

6 结论

本文针对SS型的谐振式WPT系统电路参数同时偏移的情况，提出的一种辨识方法依靠两组待参数之间的循环寻优和互相迭代来获取最优解。得到的结论如下：

1）通过使用本文所提出的方法来对SS型的谐振式WPT系统的4个谐振电路参数进行辨识可以避免传统PSO算法的局部最优问题。用此方法经过两到三轮辨识基本都会收敛到较为准确的解。

2）仿真和实验结果表明，在寻找最优解的过程中添加的关于二次侧特征频率的约束条件可以起到较好的限制作用，并可以排除掉大量的非期望解。

3）每一次辨识过程都会根据两组参数之间的灵敏度关系来调整适应度函数里面惩罚项系数，从而可以减小因为两组参数之间灵敏程度太强引起的误差，以达到非常高的辨识精度。

所提出方法适用于多个参数同时发生偏移的复杂情况。本文主要是对SS型谐振式WPT系统进行分析，理论上来说该方法同样适用于其他类型的WPT系统的多参数辨识。

[1] Kim J, Kim H, Kong S, et al. Coil design and shielding methods for a magnetic resonant wireless power transfer system[J]. Proceedings of the IEEE, 2013, 101(6): 1332-1342.

[2] 贾金亮, 闫晓强. 磁耦合谐振式无线电能传输特性研究动态[J]. 电工技术学报, 2020, 35(20): 4217- 4231.

Jia Jinliang, Yan Xiaoqiang. Research tends of magnetic coupling resonant wireless power transfer characteristics[J]. Transactions of China Electro- technical Society, 2020, 35(20): 4217-4231.

[3] Wu Lihao, Zhang Bo, Zhou Jiali. Efficiency improve- ment of the parity-time-symmetric wireless power transfer system for electric vehicle charging[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12497-12508.

[4] 苑朝阳, 张献, 杨庆新, 等. 无线供电高铁列车非对称耦合机构[J]. 电工技术学报, 2017, 32(18): 18-25.

Yuan Zhaoyang, Zhang Xian, Yang Qingxin, et al. Asymmetric coupling mechanism of wireless power transmission system for high-speed train[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(18): 18-25.

[5] 徐桂芝, 李晨曦, 赵军, 等. 电动汽车无线充电电磁环境安全性研究[J]. 电工技术学报, 2017, 32(22): 152-157.

Xu Guizhi, Li Chenxi, Zhao Jun, et al. Electro- magnetic environment safety study of wireless electric vehicle charging[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 152-157.

[6] 吴丽君, 李冠西, 张朱浩伯, 等. 一种具有恒流恒压输出自切换特性的电动汽车无线电能传输系统拓扑[J]. 电工技术学报, 2020, 35(18): 3781-3790.

Wu Lijun, Li Guanxi, Zhang Zhuhaobo, et al. A wire- less power transfer system topology with automatic switching characteristics of constant current and con- stant voltage output for electric vehicle charging[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3781-3790.

[7] Mou Xiaolin, Gladwin D T, Zhao Rui, et al. Survey on magnetic resonant coupling wireless power transfer technology for electric vehicle charging[J]. IET Power Electronics, 2019, 12(12): 3005-3020.

[8] Liu Jun, Wang Chang, Wang Xiaofeng, et al. Fre- quency splitting and transmission characteristics of MCR-WPT system considering non-linearities of compensation capacitors[J]. Electronics, 2020, 9(1): 1-20.

[9] 何祥瑞, 荣灿灿, 刘明海, 等. 基于无线电能传输系统多线圈结构参数优化设计[J]. 电工技术学报, 2021, 36(增刊2): 404-411.

He Xiangrui, Rong Cancan, Liu Minghai, et al. Optimization design of multi-coil structure para- meters based on wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 404-411.

[10] Kawamura A, Kim T W. Proposed equivalent circuit and parameter identification method for electro- magnetic resonance based wireless power transfer[J]. Journal of Electrical Engineering & Technology, 2013, 8(4): 799-807.

[11] Zheng Peikun, Lei Wanjun, Liu Fenghua, et al. Primary control strategy of magnetic resonant wire- less power transfer based on steady-state load identification method[C]//International Power Elec- tronics and Application Conference and Exposition (PEAC), Shenzhen, China, 2018: 1-5.

[12] Su Yugang, Chen Long, Wu Xueying, et al. Load and mutual inductance identification from the primary side of inductive power transfer system with parallel- tuned secondary power pickup[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9952-9962.

[13] Su Yugang, Zhang Hongyan, Wang Zhihui, et al. Steady-state load identification method of inductive power transfer system based on switching capa- citors[J]. IEEE Transactions on Power Electronics, 2015, 30(11): 6349-6355.

[14] Yue Kang, Liu Yu, Zhao Peng, et al. Coupling coefficient and load estimation for wireless power transfer systems with transmitter side input current[C]// IEEE Applied Power Electronics Conference and Exposition (APEC), Electr Network, 2021: 709-713.

[15] 李中启, 李上游, 李晶, 等. 动态无线电能传输系统多接收线圈正反串联结构的互感计算与优化[J]. 电工技术学报, 2021, 36(24): 5153-5164.

Li Zhongqi, Li Shangyou, Li Jing, et al. Mutual inductance calculation and optimization of multi- receiver positive and negative series coil structure in dynamic wireless power transfer systems[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(24): 5153-5164.

[16] 程志远, 陈坤, 李东东, 等. 旋转式无线充电系统偏移特性研究[J]. 电工技术学报, 2021, 36(22): 4648-4657.

Cheng Zhiyuan, Chen Kun, Li Dongdong, et al. Research on offset characteristics of rotary wireless charging system[J]. Transactions of China Electro- technical Society, 2021, 36(22): 4648-4657.

[17] Song Kai, Li Zhenjie, Jiang Jinhai, et al. Constant current/voltage charging operation for series-series and series-parallel compensated wireless power transfer systems employing primary-side controller[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 8065-8080.

[18] Wang Zhihui, Lü Xiao, Sun Yue, et al. A simple approach for load identification in current-fed inductive power transfer system[C]//IEEE Inter- national Conference on Power System Technology (POWERCON), Auckland, USA, 2012: 1-5.

[19] Guo Yanjie, Zhang Yuwang, Li Shufan, et al. Load parameter joint identification of wireless power transfer system based on the DC input current and phase-shift angle[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10542-10553

[20] Yin Jian, Lin Deyan, Lee C K, et al. Front-end monitoring of multiple loads in wireless power transfer systems without wireless communication systems[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 2510-2517.

[21] Wang Zhihui, Li Yupeng, Sun Yue, et al. Load detection model of voltage-fed inductive power transfer system[J]. IEEE Transactions on Power Elec- tronics, 2013, 28(11): 5233-5243.

[22] Yin Jian, Lin Deyan, Lee C K, et al. A systematic approach for load monitoring and power control in wireless power transfer systems without any direct output measurement[J]. IEEE Transactions on Power Electronics, 2015, 30(3): 1657-1667.

[23] Liu Fang, Zhao Zhengming, Zhang Yiming, et al. A selection method of mutual inductance identification models based on sensitivity analysis for wireless electric vehicles charging[C]//IEEE Energy Con- version Congress and Exposition (ECCE), Milwaukee, USA, 2016: 1-6.

[24] Chow J P W, Chung H S H. Use of primary-side information to perform online estimation of the secondary-side information and mutual inductance in wireless inductive link[C]//IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, USA, 2015: 2648-2655.

[25] Liu Junwei, Wang Guibin, Xu Gang, et al. A parameter identification approach with primary-side measurement for DC-DC wireless-power-transfer converters with different resonant tank topologies[J]. IEEE Transaction on Transportation Electrification, 2021, 7(3): 1219-1235.

[26] Yin Jian, Lin Deyan, Parisini T, et al. Front-end monitoring of the mutual inductance and load resistance in a series-series compensated wireless power transfer system[J]. IEEE Transactions on Power Electronics, 2016, 31(10): 7339-7352.

[27] Dai Xin, Li Xiaofei, Li Yanling, et al. Maximum efficiency tracking for wireless power transfer systems with dynamic coupling coefficient esti- mation[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5005-5015.

[28] Dai Xin, Jiang Jincheng, Xu Zhou, et al. Cooperative control for multi-excitation units WPT system with multiple coupling parameter identification and area adaptation[J]. IEEE Access, 2020, 8: 38728-38741.

[29] Zhu Qing, Yuan Xiaofang, Wang Hui. An improved chaos optimization algorithm-based parameter identi- fication of synchronous generator[J]. Electrical Engineering, 2012, 34(3): 147-153.

[30] 郭丽莎, 罗志超, 魏学哲. 基于最小二乘法的无线充电线圈自感辨识[J]. 汽车工程, 2017, 39(10): 1217-1222.

Guo Lisha, Luo Zhichao, Wei Xuezhe. The identi- fication of the self-inductance in wireless charging coils based on least square method[J]. Automotive Engineering, 2017, 39(10): 1217-1222.

[31] Kobayashi D, Imura T, Hori Y. Real-time coupling coefficient estimation and maximum efficiency control on dynamic wireless power transfer for electric vehicles[C]//IEEE PELS Workshop on EmergingTechnologies: Wireless Power (2015 WOW), Daejeon, Korea, 2015: 1-6.

[32] Wang Quandi, Wang Yingcong, Kang Jianwei, et al. Parameter identification of wireless power transfer with a movable receiver[J]. COMPEL-The Inter- national Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2017, 36(6): 1580-1593.

[33] Xing Chen, Liu Tingzhang, Zhao Jianfei, et al. Parameter identification of primary side in wireless charging system based on adaptive particle swarm optimization[C]//Chinese Control Conference (CCC), Wuhan, China, 2018: 1667-1671.

[34] Liu Liangjiang, Li Qingxian, Liu Liang, et al. Parameter identification of wireless power transfer system using parallel chaos optimization algorithm[C]// Chinese Automation Congress (CAC), Jinan, China, 2017: 7549-7554.

[35] 苏玉刚, 陈龙, 吴学颖, 等. 基于遗传算法的SS型磁耦合WPT系统负载与互感识别方法[J]. 电工技术学报, 2018, 33(18): 4199-4206.

Su Yugang, Chen Long, Wu Xueying, et al. Load and mutual inductance identification method of SS-type magnetically-coupled WPT system based on genetic algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4199-4206.

[36] 赵永扬, 徐方维, 舒勤, 等. 基于背景谐波最小波动能量的系统侧谐波阻抗估计[J]. 电力系统自动化, 2019, 43(24): 142-148, 200.

Zhao Yongyang, Xu Fangwei, Shu Qin, et al. Harmonic impedance estimation on system side based on minimum fluctuation energy of background harmonic[J]. Automation of Electric Power Systems, 2019, 43(24): 142-148, 200.

[37] Lin Deyan, Yin Jian, Hui S Y R. Parameter identi- fication of wireless power transfer systems using input voltage and current[C]//IEEE Energy Con- version Congress and Exposition (ECCE), Pittsburgh, USA, 2014: 832-836.

[38] Qu B Y, Suganthan P H, Nas S. A distance-based locally informed particle swarm model for multimodal optimization[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(3): 387-402.

Online Identification of Joint Parameters of Electric Vehicle Wireless Charging System Based on Loop-Iteration Particle Swarm Optimization

（School of Mechatronic Engineering and Automation Shanghai University Shanghai 200444 China）

Parameters drift in wireless power transfer system often affects the charging efficiency and transmission power of the system. A joint parameter online identification method for resonant wireless power transfer systems was proposed in this paper. First, the circuit equations were established based on the equivalent resonant circuit. Secondly, a model of feature variable is established. Then the input voltage on the primary side, the real-time current on the primary side and the secondary side were detected and performed Fourier transform to obtain the characteristic frequency. On this basis, a fitness function containing only 4 unknowns (1,1,2,2) was constructed. The parameter identification problem was transformed into a function optimization problem. A loop-iteration particle swarm optimization algorithm was proposed to find the optimal solution of unknown parameters. The 4 parameters to be identified are divided into two groups. Primary capacitance1and inductance1are the first set, secondary capacitance2and inductance2are the second one. Only one set of parameters are identified each time, and the identification results are taken as the initial conditions of the optimization process of the other set. Finally, the simulation and experiment show that the proposed scheme can identify each parameter effectively when four parameters drift simultaneously in WPT system, and can achieve high accuracy.

Parameters drift, wireless power transfer, joint parameter identification, loop-iteration particle swarm optimization

10.19595/j.cnki.1000-6753.tces.211943

TM724

高等学校学科创新引智计划资助项目（D18003）。

2021-11-29

2022-03-19

刘廷章 男，1967年生，教授，博士生导师，研究方向为智能电网用户侧系统建模与控制、设备故障诊断与容错。E-mail: liutzhcom@oa.shu.edu.cn（通信作者）

张子恒 男，1997年生，硕士研究生，研究方向为电力系统故障诊断。E-mail: zzh673912328@163.com

（编辑 陈 诚）