U型渡槽参数化有限元建模与智能优化设计研究
2022-09-26张建华林潮宁黄永涛李同春
张建华,李 静,林潮宁,黄永涛,李同春
(1.中铁水利水电规划设计集团有限公司,江西 南昌 330029; 2.河海大学水利水电学院,江苏 南京 210098;3.河海大学土木与交通学院,江苏 南京 210098)
渡槽是跨越河渠、道路、谷口、山冲等输送渠道水流的架空输水建筑物,除用于输送渠水进行农田灌溉、城镇生活用水、工业用水、跨流域调水外,还可用于排洪和导流[1-2]。渡槽由槽身、支承结构及进出口建筑物等部分组成,是渠系建筑物中应用最广泛的交叉建筑物之一[3-4]。渡槽的结构形式、截面尺寸及配筋是否合理,将影响输水工程的投资、工期和工程量。为保障渡槽的安全运行,降低工程造价,有必要对渡槽的结构优化设计问题进行研究和讨论。
结构优化设计是指设计者根据设计要求,在满足规范或特定要求的条件下,利用数学手段使所选定的目标函数(如重量、造价、刚度等)达到最优[5]。结构优化设计过程大致可分为4个阶段:第一阶段,建立数学模型,将工程结构的设计问题转化为数学问题;第二阶段,选择一个合理、有效的优化计算方法;第三阶段,编制计算机程序对问题进行求解;第四阶段,结果检验与决策[6]。
目前,对渡槽结构优化方面的研究主要集中在渡槽结构尺寸的优化、渡槽结构力学特性的优化分析及渡槽结构可靠性分析等方面。郑重阳等[7-8]以工程造价最低为优化目标,将渡槽的几何尺寸参数和预应力钢筋数量作为优化设计变量,采用了改进的遗传算法进行优化设计。张永生[9]在对拱梁组合式渡槽的组成及受力进行定性分析的基础上,建立了平面杆件有限元力学分析模型,提出了采用离散搜索组合法对渡槽上部结构进行优化设计的数学模型。任益楼等[10-11]将影响渡槽结构安全的诸多因素(结构尺寸、材料性能、作用荷载、输水能力等)作为随机变量,开展了基于可靠度理论的渡槽结构优化设计研究。
随着计算机技术和计算数学的不断进步,结构优化设计算法得到了很大的发展[12]。然而,对渡槽进行优化设计时,每次优化迭代分析后需要对设计变量进行动态修改,并对结构强度进行校核。在采用三维有限元模型进行分析时,重复性的再建模与再分析工作需要耗费大量的人力和时间。目前部分商用有限元软件为用户提供了结构优化模块,但其原有的优化模块存在一些问题:①对部分结构离散型变量的优化分析不容易得到满足约束的结果,性能不够稳定;②在计算过程中迭代次数过多,计算效率不高[13]。
为使渡槽结构优化设计向智能化、自动化、系统化发展,本文基于HSNAP加速了渡槽结构的建模速度;编制了并行化鲸鱼优化算法程序进行优化计算,解决了传统优化算法收敛速度慢等问题;运用惩罚函数法改进广义的目标函数,将多约束的目标函数转化为无约束的目标函数。在此基础上,建立了一套结合参数化有限元分析程序及智能优化算法程序的渡槽结构优化设计系统。以某灌区U型渡槽工程为例,采用所提出的优化设计系统对渡槽槽身结构进行优化设计,在保障渡槽安全运行的前提下,达到节约工程投资的目的。
1 U型渡槽参数化有限元建模
1.1 建模基本流程
U型渡槽的结构分析采用有限元法。为减少有限元分析计算中几何建模、网格划分、物理属性定义及结构后处理的工作量,采用参数化有限元建模方法,基于自主研发的大型有限元通用程序HSNAP,开发结构参数化建模程序模块,形成快速、高效的渡槽结构参数化有限元分析流程。HSNAP程序是河海大学李同春教授及其团队研发的水工结构有限元数值分析程序,采用Fortran语言编写,具备水工结构分析中常用的静、动力分析,渗流场、温度场分析等功能[14]。
U型渡槽参数化有限元分析基本流程如图1所示。渡槽结构参数化建模过程包括渡槽几何模型的参数化、网格划分参数化,以及材料属性、荷载和边界条件定义等的参数化。
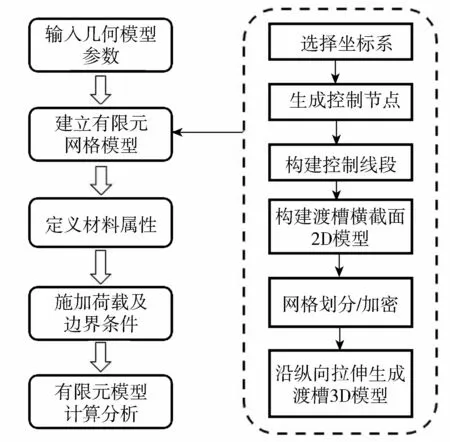
图1 U型渡槽参数化有限元分析基本流程Fig.1 Flowchart of parametric finite element analysis of U-shaped aqueduct
1.2 参数化建模方法
U型渡槽由槽身、肋板以及拉杆构成[15],本文提取渡槽的几何特征参数,对渡槽进行三维参数化建模。如图2所示,渡槽横截面几何特征参数有R0、t、t0、a、b、c、f、d0、S0、t1、t2、H、L和α。在参数化建模过程中,模型结构按点、线、面、体的顺序自动化建模,具体步骤如下:
a.输入几何模型参数。
b.建立Oxyz整体坐标系。y轴为水平向,z轴为竖向,x轴为顺槽向且指向渡槽下游;在Oyz坐标系内建立渡槽横截面2D模型,沿x方向拉伸生成渡槽3D模型。
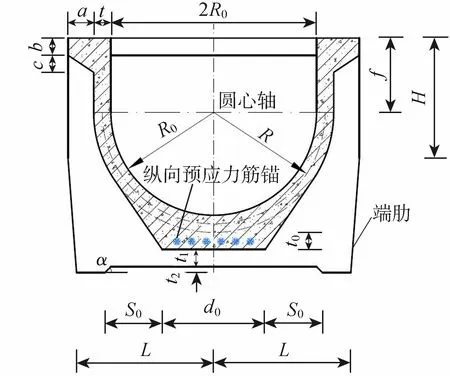
图2 U型渡槽横截面示意图Fig.2 Cross section of U-shaped aqueduct
c.生成控制节点。定义渡槽横截面顶部中心点为坐标原点;根据渡槽几何尺寸参数,得到相对坐标原点的各控制节点坐标,图3为渡槽横截面上的控制节点及节点编号。
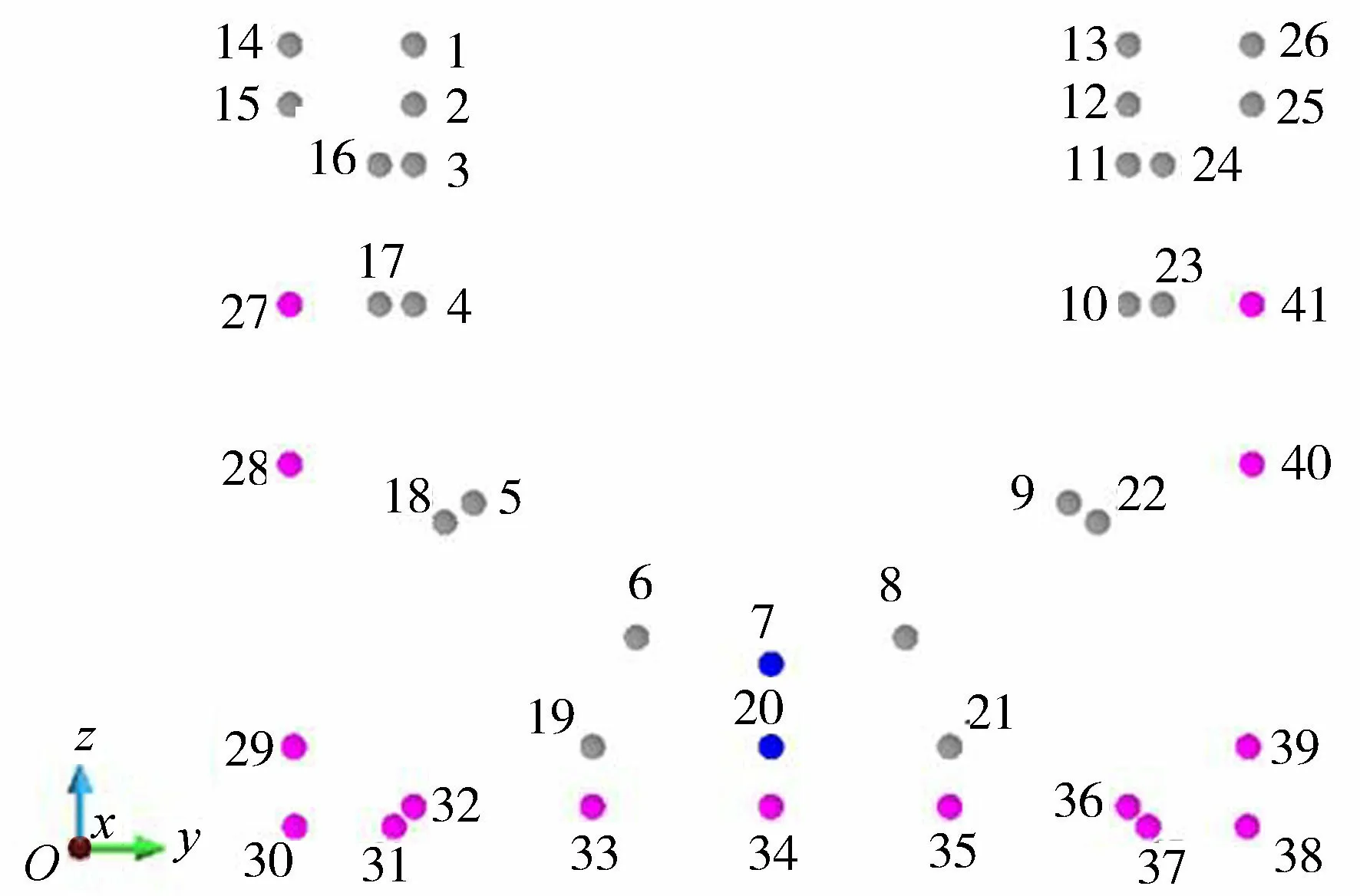
图3 U型渡槽横截面上的控制节点Fig.3 Key nodes on cross section of U-shaped aqueduct
d.构建渡槽槽身和肋板控制线段。将控制点相连接,构建控制线段集(图4),线段类型可为直线型或圆弧型。
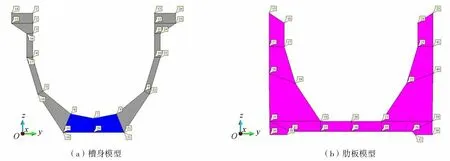
图4 渡槽横截面2D模型Fig.4 2D model of aqueduct cross section
e.构建渡槽横截面2D模型。根据线段集上的节点信息生成四节点平面单元,构建渡槽槽身和肋板横截面2D网格模型,如图4所示。
f.网格划分/加密:对渡槽横截面(包含槽身和肋板)的初始2D网格模型进行加密,加密后的渡槽横截面网格模型如图5(a)所示。
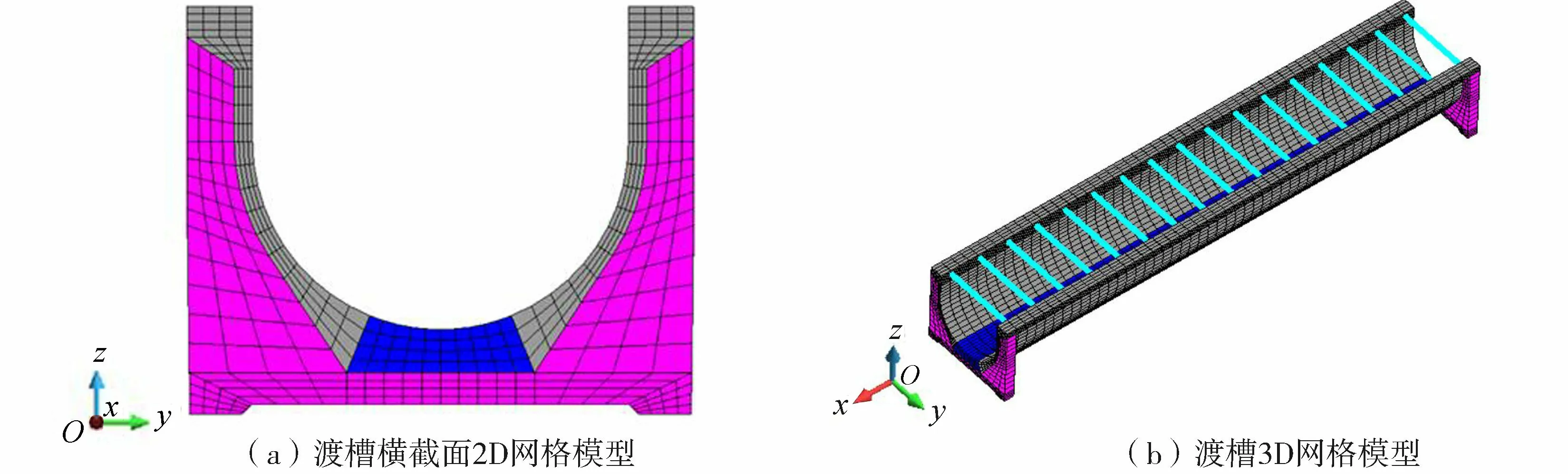
图5 加密后的渡槽2D及3D有限元网格模型Fig.5 2D and 3D finite element mesh models of aqueduct after densification
g.构建渡槽3D模型。将渡槽横截面2D网格模型沿x方向拉伸,形成基于八节点六面体单元的渡槽3D网格模型;根据设置的拉杆间距及位置,采用线单元模拟拉杆结构,如图5(b)所示。
h.定义材料属性。对槽身、肋板和拉杆的材料属性进行定义,包括杨氏模量、泊松比、密度等。
i.施加荷载及边界条件。荷载组合考虑槽身自重荷载、水荷载和风荷载;计算时,肋板底部施加固定约束。
j.对渡槽结构进行计算分析。
2 U型渡槽结构优化设计
2.1 并行化鲸鱼优化算法
Mirjalili等[16]根据鲸鱼围捕猎物的行为提出一种新型智能优化算法——鲸鱼优化算法(whale optimization algorithm,WOA),并通过多个基准测试函数进行测试,从结果上验证了该算法的可行性。通过对比,鲸鱼优化算法已被证明在算法对函数求解精度和稳定性上明显优于粒子群算法、遗传算法、进化规划算法等。为进一步提高计算效率,结合多核并行技术,利用并行化鲸鱼优化算法对渡槽结构进行优化分析。
2.1.1 鲸鱼优化算法
座头鲸可以识别猎物的位置,并对其进行包围。鲸鱼优化算法模拟该行为时以当前最优位置为基准,其他的鲸鱼个体将它们的位置向该位置更新。该包围行为的数学模型可表示为
D=CXp(t)-X(t)
(1)
X(t+1)=Xp(t)-AD
(2)

式中:t为当前迭代次数;Xp(t)为当前最优解位置向量;X(t)为鲸群个体的位置向量;X(t+1)为更新后的鲸群个体的位置向量;D为X(t)与Xp(t)之间的距离;A、C为系数,当|A|≥1时,鲸群扩大搜索范围,进行全局搜索,寻找更优的猎物位置,当|A|<1时,鲸群将会进入包围猎物阶段,进行局部搜索;a为收敛因子,在迭代过程中a的模从2到0呈线性递减;r1、r2为[0,1]上的随机系数;Tmax为最大迭代次数。
座头鲸捕食时,在收缩包围的同时进行螺旋上升的运动,该行为的数学模型可表示为
X(t+1)=eblcos(2πl)D′+Xp(t)
(3)
其中D′=X*(t)-X(t)
式中:b为控制对数螺旋线形状的常量;l为[-1,1]之间的随机量;X*(t)为迭代更新后的最优解位置向量。
假设座头鲸收缩包围和螺旋上升运动的概率均为0.5,则可建立如下数学模型:
(4)
式中p为[0,1]上的随机数。
综上所述,COPD患者的细胞免疫功能低下,HBO治疗能改善COPD患者的细胞免疫功能,增强患者抵御反复感染的能力,改善缺氧,提高肺功能,有助于临床综合治疗,减少急性发作的次数。HBO是COPD患者稳定期治疗的有效方法。
在搜索捕食中,通过设定|A|≥1,由随机选择的鲸鱼个体作为参照来更新其他鲸鱼个体的位置,迫使鲸鱼个体远离参照鲸鱼来寻找其他更合适的猎物,从而使该算法能在全局范围内进行搜索。数学模型如下:
D=CXrand(t)-X(t)
(5)
X(t+1)=Xrand(t)-AD
(6)
式中Xrand(t)为从鲸群中随机选择的鲸鱼个体的位置向量。
2.1.2 算法的并行化改进
随着计算机软硬件技术的发展,近年来,并行计算技术逐渐被应用于工程计算中[17]。相较于串行计算,并行计算是通过提高空间复杂度的方式来降低时间复杂度,以提高计算效率[18]。在并行计算中,计算线程数与CPU内核数相同,通过将任务分解为小部分,以并发方式分配给CPU的各个内核同步计算,计算完成后将结果合并。
传统的鲸鱼优化算法对鲸鱼围捕猎物的过程是串行计算,即对于每一个迭代步,一头鲸搜寻结束,下一头鲸才能启动搜寻。因此同一时间计算机只能进行一次有限元正分析,优化过程耗时长。因此本文将鲸鱼优化算法与并行算法相结合,计算过程中将鲸鱼种群分为若干个子种群,将子种群分配到CPU不同内核上执行有限元正分析计算,待各子种群计算结束,再合并形成新的种群,然后进入下一迭代步。图6为并行化鲸鱼优化算法寻优过程流程图。如使用一台配置3核处理的计算机进行运算,可以节约计算时间约70%。
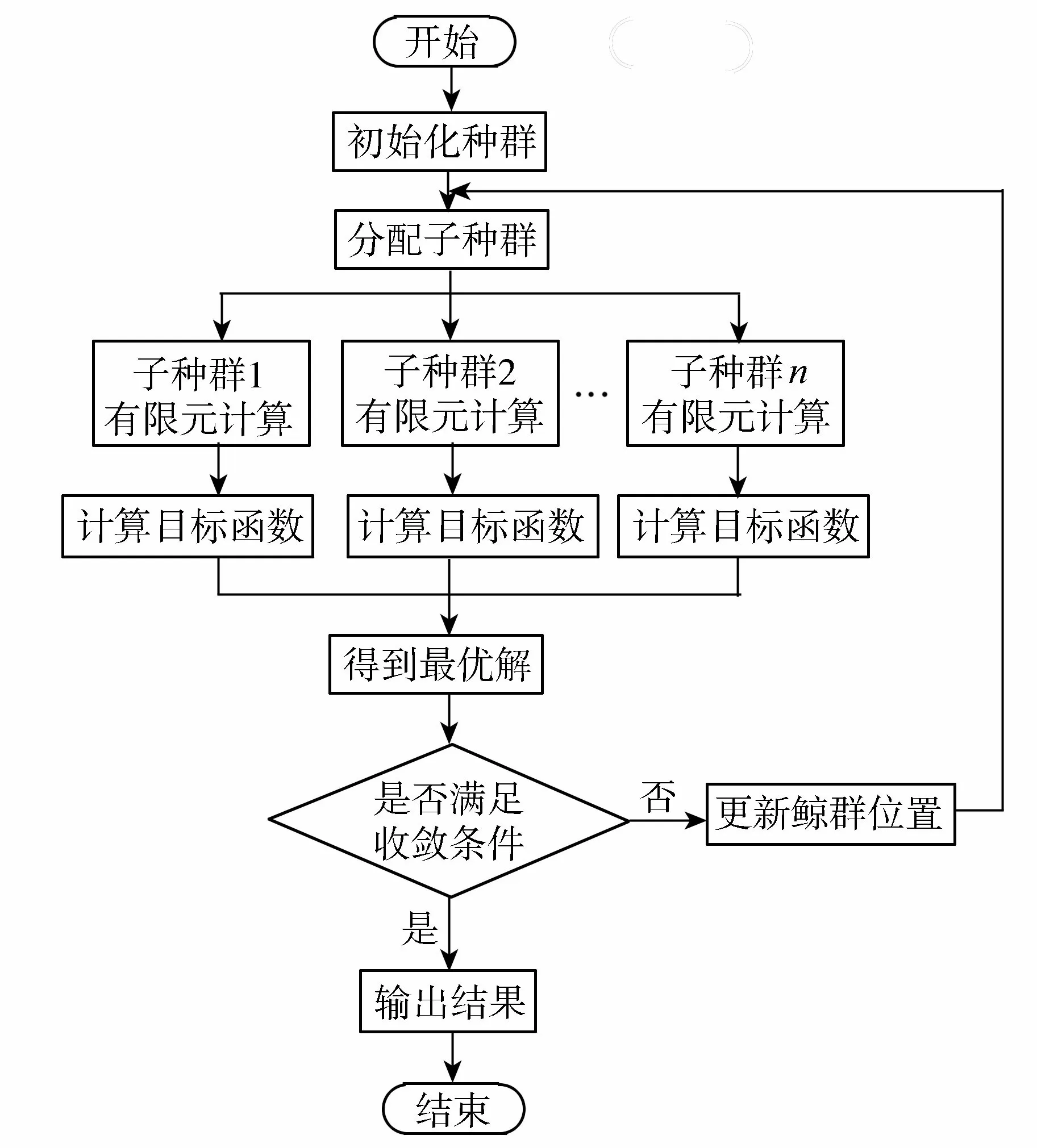
图6 并行化鲸鱼优化算法寻优过程流程Fig.6 Flowchart of paralleled whale optimization algorithm
2.2 优化目标
考虑渡槽钢筋数量不变的情况下,对渡槽槽身的横截面尺寸进行优化,以减少混凝土用量,提高工程的经济效益。图2为U型渡槽物理模型截面图,槽身的内径R0和竖直段f的尺寸根据渡槽的流量要求进行拟定;a、b、c的尺寸对渡槽结构影响较小,可根据规范进行拟定。因此,优化目标为槽身横截面面积S,待优化的设计变量为槽身横截面尺寸参数t和t0。
根据SL 191—2008《水工混凝土结构设计规范》的要求,渡槽槽身需满足以下约束条件。
a.渡槽槽身需满足预应力受弯构件斜截面抗裂要求:
(7)
式中:σtp、σcp分别为混凝土的主拉应力和主压应力;ftp、fck分别为混凝土轴心抗拉和抗压强度标准值。
b.渡槽槽身需满足预应力受弯构件正截面抗裂要求:
σx≤0.7γmftk
(8)
式中:σx为混凝土x向(顺槽向)应力;γm截面抵抗矩塑性系数。
c.对于渡槽跨中部位,槽身内侧需满足:
σx≤0
(9)
d.渡槽槽身最大挠度值需满足:
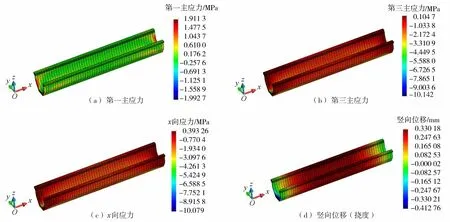
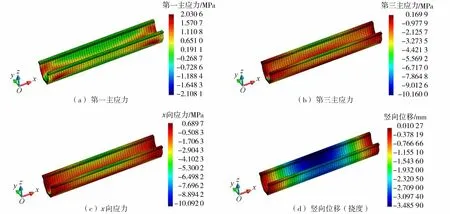
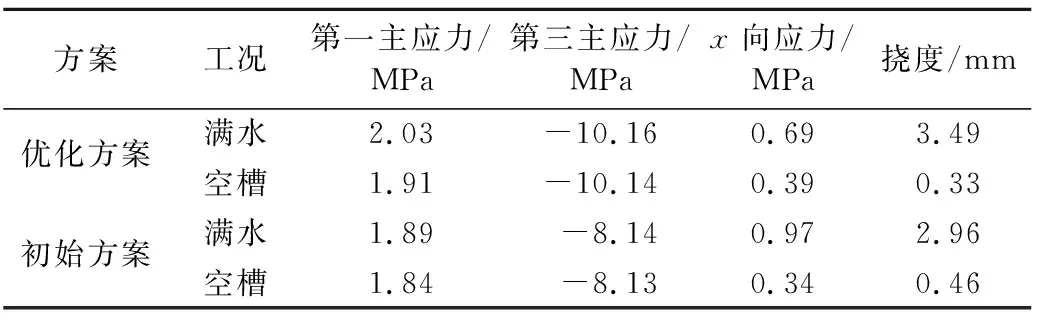
w (10) 式中:w为挠度;L为计算跨度。 针对渡槽结构优化中的离散型变量优化问题和非线性多约束优化问题,运用惩罚函数法[19]改进广义的目标函数,将多约束的目标函数转化为无约束的目标函数: (11) 式中:f(t,t′)为目标函数;S(t,t′)为优化目标,即槽身的横截面面积;u为惩罚系数。 某中型灌区设计灌溉面积2.22万hm2,该灌区共有渡槽33座,总长23.231 km。某河段渡槽槽身为预应力钢筋混凝土梁式结构,单跨25 m,槽底纵坡1/1 000。槽身断面为U型断面,如图2所示,其中R0=0.18 m、t=0.30 m、t0=0.30 m、a=0.45 m、b=0.30 m、c=0.30 m、f=1.30 m、d0=1.80 m。槽身材料为C40预制混凝土,预应力钢绞线型号为1×7φS15.2 mm,预应力施工中张拉应力为1 860 MPa,非预应力钢筋型号为HRB335。 对渡槽槽身的截面尺寸进行优化设计,优化目标为槽身横截面面积S,待优化的设计变量为t和t0。根据经验和施工要求[20],变量的取值范围定为:t=(0.10~0.30)m,t0=(1~1.5)t。计算中考虑槽身的自重荷载、水荷载(渡槽满水位)和风荷载。 优化算法采用并行化鲸鱼优化算法,分析中设置群体规模为20,最大迭代次数为50,图7为并行化鲸鱼优化算法的迭代过程趋势线。优化后的截面尺寸参数为t=0.163 m,t0= 0.244 m,对应的槽身横截面面积为2.616 m2。与原设计方案(截面尺寸参数t=0.3 m,t0=0.3 m,槽身横截面面积3.994 m2)相比,优化后的槽身横截面面积减小了34.5%。本渡槽单跨25 m,共计19跨,故共可节约混凝土654.55 m3,考虑混凝土单价为500元/m3,则可节省工程造价约32.73万元。 图7 优化迭代过程趋势线Fig.7 Iterative trend line of optimization process 对优化后渡槽结构的安全性进行分析和复核。该案例中渡槽槽身的第一主应力(主拉应力)和第三主应力(主压应力)需满足σtp≤0.85ftk=2.03 MPa,σcp≤0.60fck=16.08 MPa;槽身正截面的法向应力需满足σx≤0.7γmftk=1.81 MPa;在渡槽跨中部位和渡槽内侧不允许出现顺槽向法向拉应力,即σx≤0;此外,渡槽槽身最大挠度值需满足w 渡槽槽身在空槽和满水工况下的静力分析结果如图8、图9和表1所示。如图8所示,空槽情况下,槽身第一主应力拉应力分布于渡槽两端部位,最大拉应力为1.91 MPa。空槽情况下由于预应力的作用,在竖直方向上槽身有反拱现象,变形趋势与理论一致,最大反拱位移为0.33 mm。如图9所示,设计水深下,槽身第一主应力拉应力分布于渡槽两端和薄壁部位,最大拉应力为2.03 MPa。渡槽的挠度值为3.49 mm,满足渡槽允许的最大挠度要求。根据表1的统计结果,空槽和满水工况下,优化后渡槽的应力和变形均满足规范要求。 图8 空槽情况下渡槽槽身静力分析结果Fig.8 Static analysis results of aqueduct body under empty aqueduct condition 图9 满水工况下渡槽槽身静力分析结果Fig.9 Static analysis results of aqueduct body with full water 表1 渡槽槽身静力分析极值结果 a.采用参数化有限元建模方法,基于自主研发的大型有限元通用程序HSNAP,开发了参数化建模程序模块,实现了渡槽结构几何模型的参数化、网格划分参数化,以及材料属性、荷载和边界条件定义等的参数化,形成了快速、高效的渡槽结构参数化有限元分析流程模式。 b.针对传统优化算法收敛速度慢、计算效率低等不足,结合多核并行技术,编制了并行化鲸鱼优化算法程序进行优化计算,降低了计算的时间成本。 c.结合某灌区U型渡槽工程,以混凝土用量最低为优化目标,在满足渡槽结构强度约束条件和几何约束条件的情况下,对渡槽结构尺寸参数进行优化。分析结果表明,与原设计方案相比,优化方案能够满足结构的安全要求,且具有显著的经济效益。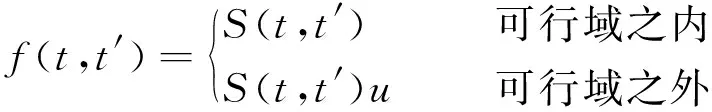
3 案例分析
3.1 工程概况
3.2 结构优化设计

3.3 有限元计算结果分析
4 结 论
