涌潮CFD数值模拟若干问题探讨
2022-09-26张芝永谢咏哲潘存鸿
张芝永,谢咏哲,陈 红,潘存鸿
(1.浙江省水利河口研究院(浙江省海洋规划设计研究院),浙江 杭州 310020;2.浙江省河口海岸重点实验室,浙江 杭州 310020;3.河海大学水利水电学院,江苏 南京 210098)
涌潮是外海潮波进入逐渐缩窄的宽浅河口后发生剧烈变形而引起的一种特殊水力学现象[1],主要发生在喇叭形的入海河口。我国钱塘江涌潮是世界著名的涌潮景观,其涌潮强度及气势世界罕有。涌潮类似于移动的水跃,其水流形态及流场结构极为复杂,极强的水流冲击导致海塘、丁坝等[2]涉水工程破坏严重,同时也会导致河床的剧烈冲刷和大量泥沙的悬浮,对河床冲淤影响极大[3]。因此研究涌潮的局部水动力特性及其与结构物、河床的作用机理有助于为涌潮河段的结构物及河床冲刷防护方案的实施提供技术支撑。
目前对于涌潮的研究普遍集中于大尺度方面,如对涌潮在整个河口区传播规律的研究:潘存鸿等[4]基于KFVS格式开发了第一个可以精准模拟涌潮的大范围二维数值计算模型,谢东风等[5-7]先后应用FVCOM对钱塘江涌潮进行了三维数值模拟。以上学者在数值模型中均是利用外海边界的规则潮波进入逐渐束窄河段后发生潮波变形而自然生成的涌潮,但其模型均因采用基于浅水方程简化的二维或三维数值模型而无法解决局部建筑物的涌潮作用力及局部冲刷等问题。
对于涌潮与局部建筑物及河床相互作用问题的研究,需要借助基于Navier-Stokes方程的CFD数值模型或涌潮试验水槽。在数学模拟或试验模拟过程中,由于计算资源或试验模型空间的限制,无法构建足够长的束窄过渡段,只能通过规则潮波的自然变形来生成涌潮。为此,如何在边界处直接生成涌潮成为许多涌潮学者关注的问题。近年来,随着水泵测控、闸门控制技术的进步,一些学者相继提出了在边界处直接构造涌潮的生潮方法,使得涌潮局部尺度问题的研究成为可能。如黄静等[8-9]通过调节水槽末端水泵频率使流量发生突变的方法在实验室内实现了涌潮的准确模拟,但因流量突变幅度与涌潮高度的相关性未知,在试验中需要多次调试才能得到预期的涌潮水流。而Chanson等[10-12]则基于落闸法得到了反向涌潮波,但其生成的涌潮的底部水流与表层水流运动方向完全相反,这与河口区涌潮传播过程中的流态结构完全不同。数值模拟方面,已有CFD数值模拟研究中常将涌潮概化为无涨潮流速的溃坝波[13],但实际上涌潮除了涌潮高度外还伴随有一定的涨潮流速,且涨潮流速不能随意给定,它是与涌潮高度、潮前水深和落潮流速有关的参数。戎贵文等[14-16]直接在边界处设置实测水位及流速值进行涌潮的模拟,取得了较好的效果,但该方法只能针对特定的涌潮工况。戚蓝等[17-18]借鉴潘存鸿提出的涌潮条件基本方程,推导出与涌潮高度、潮前水深、落潮流速有关的涌潮涨潮流速计算方法,并应用数值模型分别进行了同时考虑水深和涨潮流速的涌潮模拟,与理论结果进行对比验证了边界生潮法的可靠性。
综上所述,目前物理模型试验和数值计算模型中成熟的涌潮生成方式有所不同,物理模型试验普遍采用流量生潮方法,而数值计算模型则是采用边界生潮方法。因无法确定流量生潮法和边界生潮法生成的涌潮水动力特性是否存在区别及数值模型中湍流模型、网格尺度等参数对涌潮精确模拟的影响,有必要对比现有涌潮生成方法的差别及其内在联系,探讨网格尺度、湍流模型选择对涌潮模拟的影响,提出适用于涌潮模拟的生潮方法、网格划分策略及湍流模型选择,进而为后续涌潮对局部结构物及河床冲刷影响的研究提供关键的数值模拟工具。
1 涌潮特性介绍
在涌潮传播过程中,涌潮以一定的水位差H和流速向上游传播,具体形式见图1,其行进方向的前方称为潮前,反之称为潮后。 图中潮头行进的速度c称为涌潮传播速度。潮前水深是涌潮到来之前河道(水槽)中的初始水深h0,此时水体可能是静止的,也可能存在一定的潮前流速(或落潮流速),即涌潮到来之前水体的流速v0,一般与涌潮传播速度相反,代表了径流在涌潮现象中的作用;h1为涌潮经过之后的水深即潮后水深,或称为涨潮水深,潮后水深与潮前水深的差值为涌潮高度H,v1为涨潮时的流速,即潮后流速(或涨潮流速)。

图1 涌潮潮头结构Fig.1 Tidal bore structure
根据涌潮形态及涌潮波破碎情况的不同,涌潮可分为3种:①潮头未发生破碎的波状涌潮;②潮头破碎强烈的强旋滚涌潮;③介于两者之间的称为弱旋滚涌潮[19]。
涌潮可视为一种移动的水跃。通过空间相对速度变换并联立一维连续性方程和动量方程,可得到涌潮各要素满足如下方程:
(1)
(2)
由式(1)(2)可知,如已知v0、h0、h1(或H),则可得c,继而由c可推求v1。
2 数 值 模 型
2.1 控制方程
局部尺度涌潮数值模拟的控制方程为连续性方程和动量方程(Navier-Stokes方程)。
2.2 自由液面追踪方法
自由面的捕捉采用高精度的VOF方法。VOF法构建了一种体积函数以追踪单元网格中的流体体积,通过其函数值及导数值确定自由面位置,适用于不可压缩、黏性、瞬变流体的问题。
2.3 湍流模型
选择较为常见的标准k-ε和RNGk-ε两种湍流模型来比较各模型模拟涌潮的效果。标准k-ε模型由k方程(即湍流动能方程)与ε方程(耗散方程)组成,因简单高效而应用广泛。RNGk-ε模型全称为重整规化群(RNG)k-ε模型[17],该模型修改了耗散方程并考虑了湍流涡旋,精度有所提高。重整规化群理论为k-ε方程提供了湍流Prandtl数,而标准k-ε模型中这一参数取经验值。RNGk-ε模型还增强了模拟低雷诺数流动的能力,使其具有更高的泛用性与可靠性,能够更好地模拟大曲率流动问题。
2.4 数值水槽中生潮边界构造
为了检验流量生潮法、边界生潮法的差异及内在联系,构建长50 m、高0.5 m的数值水槽,以便观察涌潮自生潮边界出现后向上游行进、发展的过程。边界生潮法的边界设置情况如图1所示。边界需同时给定流速和水深条件,其中水深为潮前水深叠加涌潮高度后的潮后水深h1,流速为v1,在给定v0、h0及H的情况下,可通过式(1)(2)求解得到。对于流量生成法,数值模拟中生潮边界的构造参考了模型试验的布置情况,在长水槽下游增加一段长度和深度均为1 m的生潮前室,前室下游侧为固壁,前室底部为流量进口边界,对应特定涌潮工况,生潮流量的大小需在模拟过程中经不断调试得到。
2.5 数值模拟计算方案
针对生潮方法、湍流模型及网格尺度对涌潮模拟的影响,设计15组数值模拟方案,见表1。数值模拟中潮前水深保持为0.15 m时,涌潮高度分别取0.05 m、0.10 m和0.15 m,其对应的涌潮形态分别为波状涌潮、弱漩滚涌潮和强漩滚涌潮。网格尺度影响方面,在水位波动影响区的网格尺寸d(垂向和纵向网格尺寸一致)分别取0.050H、0.100H、0.125H和0.250H。

表1 数值模拟研究方案
3 模拟结果及分析
3.1 生潮方法比较

表2 不同生潮方法对应的边界条件参数
在数值模拟中发现,对于边界生潮法,给定合理的边界水深和涨潮流速后模拟得到的涌潮高度基本与边界处一致。而流量生潮法则需要通过不断调试进口流量[20],才能得到与边界生潮法一致的涌潮高度。表2为应用两种生潮方法时各涌潮高度对应的边界条件值,其中v1由式(1)(2)联立求解推求出。
针对涌潮涨潮流速、水面线形态及涌潮传播速度对两种生潮方法模拟得到的涌潮进行对比,以x=15 m处为监测断面,选取两个典型时刻:①潮头到达监测断面使纵向流速达到极值时,对于波状涌潮即首个波峰,②潮头经过监测断面,对于波状涌潮即首个波谷,对各方法生成的涌潮潮头形态、涌潮内部纵向流速及传播速度进行对比。图2为波状涌潮(H=0.05 m)及强旋滚涌潮(H=0.15 m)在两个典型时刻的水面线情况。由图2可见,对于波状涌潮,流量生潮法和边界生潮法生成的波峰、波谷高度基本一致,但波长略有不同,对比来看,流量生潮法得到的波长要大于边界生潮法。而对于强旋滚涌潮来说,两种方法生成的涌潮潮头水面线非常接近。从流速最大时刻来看,波状涌潮流速最大值发生在首峰时刻,而旋滚涌潮则发生在涌潮升高的过程中。
图3对应图2,为不同生潮方法下x=15 m断面不同典型时刻的纵向流速u垂向分布情况。由图3可见,当波状涌潮首锋及旋滚涌潮纵向流速最大时,纵向流速垂向分布可分为两个区域:潮前水深(0.15 m)以上区域,流速迅速增大,并在自由表面处达到极值;潮前水深以下区域纵向流速则略有减小,其流速变化率明显小于潮前水深以上部分。整体来看,此时涌潮纵向流速垂向分布呈Γ型,各类涌潮均呈现相同规律。从流速大小看,涌潮高度越大,其自由表面处流速及潮前水深以下区域的平均流速相应也会增大。而在涌潮经过x=15 m后,潮前水深以上区域纵向流速有所减小。对于波状涌潮工况,纵向流速仅是其最大纵向流速的1/4。由于两种方法生成的潮头波长有所区别,波谷时刻流速也有所差异,差值在0.1 m/s左右。而对于旋滚涌潮,潮头经过后的断面最大纵向流速减小幅度约40%。对比图3中两种生潮方法的流速垂向分布情况,除了波状涌潮波谷时刻流速分布略有差异外,其他时刻两种方法生成的涌潮内部流速结构基本接近。
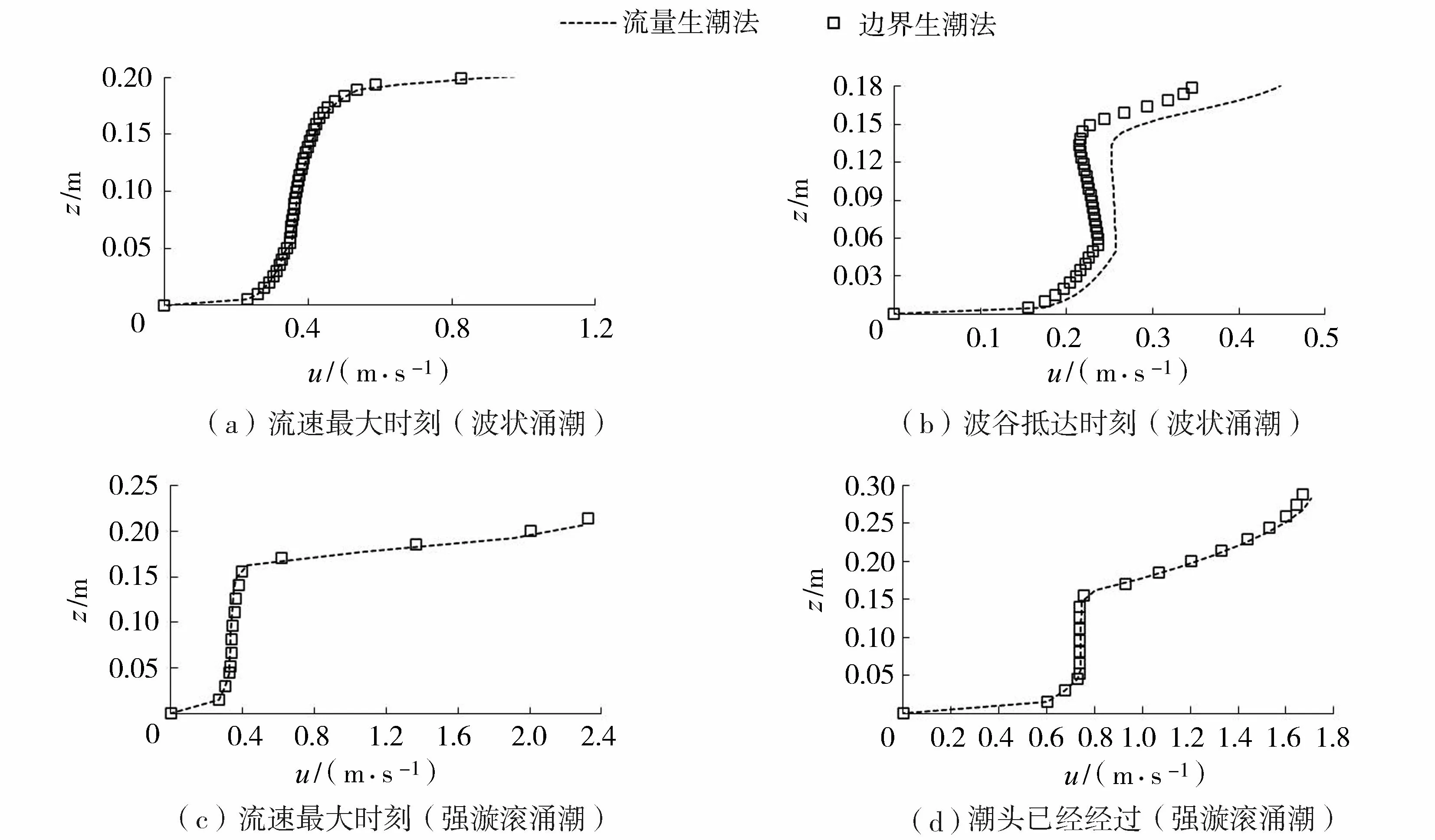
图3 不同生潮方法典型时刻纵向流速垂向分布Fig.3 Vertical distribution of longitudinal velocity using different bore generation methods
利用涌潮自x=10 m传播至x=15 m位置的时间,计算得到各组次涌潮传播速度[21],并与式(1)或式(2)计算得到的理论值进行对比。由图4可见,涌潮高度0.05 m、0.10 m和0.15 m对应的传播速度理论值分别是1.513 m/s、1.808 m/s和2.101 m/s,涌潮传播速度随着涌潮高度的增大而增大。边界生潮法和流量生潮法模拟得到的涌潮传播速度与理论值之间的平均相差幅度分别为0.8%和2.3%,基本接近。针对涌潮高度分别为0.05 m、0.10 m和0.15 m的3种涌潮工况在水槽中开展模型试验,测量各工况下的涌潮传播速度,其与数值模拟结果的对比结果见图4。总体来说,水槽试验结果略小于理论值和数值模拟结果,其原因主要是水槽试验中流量突变是依靠水泵频率的急速提升实现的,而水泵造成的流量抬升在实际情况中必将经历一个短时的过渡过程,并非数学模拟中生潮流量的瞬间变化,这造成了涌潮动力的减弱,因此水槽试验得到的涌潮传播速度相对略小。尽管如此,水槽试验结果与理论值的偏差基本在10%以内,模拟效果较好。

图4 涌潮传播速度对比Fig.4 Comparisons of bore propagation velocity
综上所述,流量生潮法和边界生潮法生成的涌潮在涌潮形态、水流流速及传播速度上均较为接近,说明两者在适当边界条件下可生成特征相同的涌潮水流。而在相同涌潮条件下,流速分布及水面线形态的一致性表明,两种方法在单位时间内的过水流量应是一致的。对比表2发现,应用流量生潮法和边界生潮法模拟3种涌潮工况时生潮边界处的单宽流量基本相同,因此确定流量生潮法的流量边界条件时可利用边界生潮法的计算公式。即:
q=v1h1
(3)
式(3)中v1由式(1)(2)确定。故采用流量生潮法时可采用式(3)估算生潮流量,从而避免了试验中需要不断调试流量的问题。值得注意的是,在水槽试验中水泵频率突变后流量提升所需要的时间也是影响涌潮生成质量的一个主要因素,过长的流量提升时间将会减弱生成涌潮的强度。因此物理模型试验中必须配置性能优、反应速度快的变频水泵才能更好地复演涌潮过程。
3.2 网格尺度影响
对于数值模拟计算来说,模型网格尺寸对数值模拟结果同样会有较大影响。适当、精细的网格能得到精确的结果,而另一方面网格尺寸将直接影响计算时间,其一个数量级的变化会导致计算时间大幅增加。 对于涌潮这一强间断水流来说,如何选择合适的网格尺寸以准确刻画其潮头特征是数值模拟中较为重要的问题。为此选用不同的相对网格尺寸进行研究,取各级网格尺寸d分别为H的0.050、0.100、0.125和0.250倍。图5为不同网格尺度下旋滚涌潮潮头水面线特征。由图5可以看出,各网格尺寸下涌潮高度是基本接近的,但在潮头水面坡度线(陡度)方面则略有差别,具体表现为网格尺度越小,涌潮潮头刻画越为精细,其潮头平均坡度会越陡,在网格尺寸小于0.100H时,模拟结果变化基本很小。

图5 各网格尺寸下的漩滚涌潮潮头水面线Fig.5 Water surface profiles of breaking tidal bore under different mesh sizes
3.3 湍流模型的影响
对于涌潮这一强间断流来说,湍流模型的选择至关重要。为此针对不同涌潮,分别应用标准k-ε模型和RNGk-ε模型进行模拟分析。图6对比了不同湍流模型下两种涌潮水面线的模拟情况。总体来看两种湍流模型得到的涌潮水面线基本接近,相比而言,采用标准k-ε模型的模拟结果其潮头水位略低于RNGk-ε模型模拟结果。而从旋滚涌潮(H=0.15 m)工况中还可以看出,标准k-ε模型的水面线坡度相对RNGk-ε模型的模拟结果更缓,说明RNGk-ε模型更适用于模拟高强度、高陡度的涌潮。

图6 各湍流模型下的涌潮潮头形态Fig.6 Tidal bore profile under different turbulent models
3.4 原型尺度涌潮的数值模拟验证
为了验证本文数值模拟方法是否可以用于原型尺度的涌潮模拟,利用2010年海宁盐官涌潮观测资料进行模型验证。2010年实测涌潮特征如表3所示。

表3 海宁盐官2010年实测涌潮资料
利用垂向二维涌潮数值水槽,根据涌潮模拟策略对表3中的3种实测大、中及小涌潮进行了模拟。图7为小潮及大潮情况下涌潮传播过程中纵向流速分布情况。由图7可见,对于涌潮高度为0.8 m的小潮,由于涌潮高度较小,水动力强度稍弱,其涌潮潮头呈现波状涌潮特征;而涌潮高度为2.74 m的大潮潮头旋滚非常强烈,数值模拟得到的涌潮形态与实际的涌潮形态基本一致。图8对比了数值模拟涌潮与实测涌潮的传播速度,可见原型尺度与实验室尺度下的涌潮传播速度规律相同,涌潮高度越大,传播速度越快,而且数值模拟得到的涌潮传播速度与实测值基本接近,平均偏差在9%以内。

图7 涌潮纵向流速及形态数值模拟结果Fig.7 Contours of longitudinal velocity and bore shapes from numerical simulation

图8 涌潮传播速度实测值与数值模拟结果对比Fig.8 Comparisons of numerical results and field measured results for propagation velocity
综上所述,通过对比涌潮形态及传播速度,证明了本文数值模拟方法在模拟原型尺度局部范围涌潮时的可靠性。但值得注意的是,本文边界生潮公式(1)和(2)是在断面规则的平直河道(水槽)情况下,基于一维连续性和动量守恒方程推导得出的,公式并未考虑地形、岸线变化对涌潮水流的影响,而实际情况中一些河段的地形、岸线变化极大,针对复杂河段内的涌潮水流运动进行CFD数值模拟时,建议以实测的潮前水深、涨潮流速、涌潮高度赋予模型边界条件。
4 结 论
a.适当边界条件下流量生潮法和边界生潮法可模拟得到各项特质均较为一致的涌潮水流,其中旋滚涌潮的模拟结果最为接近。两种生潮方法在边界构造上的不同导致模拟得到的波状涌潮首峰之后水面线形态及流速分布略有差异。在传播速度上,边界生潮法模拟结果更接近于理论值。通过对比发现,流量生潮法单宽流量与边界生潮法在生潮边界处的计算流量一致,因此可通过边界生潮法公式估算流量生潮法的边界条件,这为物理模型试验中涌潮生潮流量的确定提供了参考依据。
b.网格尺度越小,模拟得到的涌潮平均陡度越陡,当网格尺寸不大于0.100H时,网格尺度对计算结果的影响较小,因此进行涌潮数值模拟时建议网格尺寸不应大于0.100H。
c.相比RNGk-ε模型,标准k-ε模型模拟得到的潮头高度略低,潮头陡度稍缓。对于高陡度及高卷曲的涌潮水流来说,RNGk-ε模型更适合于涌潮的CFD数值模拟。
d.本文涌潮局部数值模拟方法适用于岸线及地形基本稳定的河段内的涌潮水流。针对地形、岸线变化较大的河段,建议以实测的潮前水深、涨潮流速、涌潮高度等涌潮参数作为边界条件进行涌潮CFD数值模拟。
