船用双燃料发动机综合性能预测及优化

2022-09-26宋恩哲

内燃机学报 2022年5期

许朵，姚崇，马骋，宋恩哲

(哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨 150001)

压缩天然气因其储量丰富、成本低和环境友好等特点受到研究者的重视[1]，但气体燃料的使用带来了未燃碳氢、CO 等产物的增加[2].此外，天然气的加入也带来了控制参数的增加.为了使双燃料发动机处于良好的运行状态，满足日益严格的排放法规，且具有更高的经济性，需要对双燃料发动机的各个控制参数在全工况范围内进行合理的设计优化.为此，双燃料发动机建模成为了研究的第一步，为了获取建模所需的试验数据同时避免大范围试验带来的成本增加，结合 V优化和空间填充试验设计方法进行工况点设计[3]，并以此方案获取了建模所需的数据.

国内外研究者们对发动机的预测建模进行了大量研究.Subrata等[4]基于基因表达式编程预测柴油机的排放和性能；Roy等[5]基于自适应神经模糊推理对柴油/天然气双燃料发动机进行性能和排放预测.上述方法在设计中依赖研究者的先验知识，需要对系统有深入的理解.Liu等[6]采用支持向量机的方法对发动机的 NOx排放进行稳态和瞬态建模，并取得了较好的结果，但输入参数较少，支持向量机的方法在输入参数较多的情况下，难以获取最优解的结果.此外，基于神经网络的建模方法因其强大的泛化能力、计算速度快和易于实现等优点受到研究者的青睐[7-10]；而发动机运行是连续的过程，排放物等生成在时间序列上是严格相关的，为了更好地处理时间相关的预测问题，长短期记忆神经网络(LSTM)进入了研究者的视线，其可以有效记忆当前时刻之前时序数据中的关键信息，并用于当前时刻的目标预测，使得预测的精度更高.戴金池等[11]使用 LSTM 神经网络对柴油机的NOx排放进行预测，并与传统的 BP(back propagation)神经网络和支持向量机法进行比较，结果表明LSTM 神经网络预测精度更高、泛化能力更强.为了在全工况范围内获得最佳的发动机性能和排放，必须解决一个多约束、多目标优化问题；对于这种多目标优化问题现在解决的办法有：(1)将多个目标通过加权求和的方法变成单一目标进行优化，如粒子群[12]、蚁群算法[13]，但权值的确定没有确切的理论依据，只能依靠人工经验，不同的权值会影响最优解的分布[14]，且未考虑各目标之间的相互影响，难以反映优化目标的真实情况；(2)对多个目标进行折衷与协调，基于 Pareto原理得到一组不存在相互支配关系的全局最优解集，再根据用户自己的需求，选择最适合自己目标的最优解.

带精英选择策略的非支配排序多目标遗传算法NSGA-Ⅱ(non-dominated sorting genetic algorithmⅡ)具有快速全局搜索能力[15]，对于发动机这种多变量、复杂的非线性优化问题，可以准确、可靠地找到全局最优解.Kakaee等[16]使用不同的多目标优化算法NSGA-Ⅱ和SPEA2(strength pareto evolutionary algorithm 2)，对压缩点火重型柴油机的运行参数进行优化，结果显示NSGA-Ⅱ表现出更好的性能，能够在较低的代中提供均匀分布的最优解决方案.Jaliliantabar等[17]使用 NSGA-Ⅱ算法对生物柴油发动机优化，使输出功率更大、污染物排放更小.Niu等[18]采用 NSGA-Ⅱ算法求解发动机 NOx和烟尘排放的Pareto最优解集，解集中的每个最优解均实现了以最小的牺牲实现最大程度的优化.上述研究取得了较好的效果，但研究局限于部分工况的优化，对于双燃料发动机的全工况优化研究还相对较少.

综上所述，笔者利用 LSTM 神经网络与 NSGA-Ⅱ算法相结合，对双燃料发动机的 NOx排放和燃油消耗率(BSFC)这两个负相关参数进行全工况综合优化.首先基于发动机台架上获取的时序数据，使用LSTM神经网络建立发动机预测模型，然后将LSTM神经网络与 NSGA-Ⅱ算法结合，获得优化目标 NOx与 BSFC的 Pareto前沿解集和其相对应的控制参数组合，最后将获得最优控制参数组合标定至 ECU，在发动机上进行试验验证.

1 试验台架

1.1 双燃料发动机和台架测试系统

试验采用一台装有压缩天然气进气系统的 6缸直列四冲程、高压共轨柴油/天然气双燃料发动机.飞轮端与电涡流测功机连接，用以提供负载，该发动机的技术参数见表1.

表1 发动机技术参数Tab.1 Engine specifications

发动机台架测试系统主要设备见表2，由空气流量计、AVL油耗仪、E+H燃气流量计、排放分析仪和测功机等组成，可以实时测量发动机的输出参数，双燃料发动机试验台架示意如图1所示.

图1 双燃料发动机试验台架示意Fig.1 Schematic diagram of dual-fuel engine

表2 主要测试设备Tab.2 Main test equipment

为了准确地描述双燃料发动机的经济指标，将天然气的消耗量根据低热值折算为柴油消耗量，使用有效燃油消耗率(BSFC)来表示.

式中：mdiesel为柴油的消耗量；mCNG为天然气的消耗量；Hudiesel为柴油低热值；HuCNG为天然气低热值.

1.2 输入/输出参数及范围

研究对象为柴油/天然气双燃料发动机，其中柴油作为引燃燃料，采用多次喷射的控制策略.在双燃料发动机的建模分析中，不仅要考虑传统对发动机性能影响较大的轨压、喷射正时和预喷油量等性能参数，还需要重点考虑天然气和柴油的配比，即双燃料发动机的替代率.Prabhakar等[19]研究发现轨压决定了柴油喷射的精确性和稳定性，随着轨压的增加，柴油雾化更好，使得发动机经济性更高，但 NOx的排放会略微增加；主喷正时是影响双燃料发动机排放与经济性的一个重要因素，推迟主喷正时，可以有效地减少NOx的排放，但会导致 BSFC的恶化[20]；赵国锋等[21]根据试验总结得出，较晚的预喷正时(30°CA BTDC)会导致 NOx的排放大幅度升高，而较早的预喷正时(60°CA BTDC)能够在有效提高经济性且保持 NOx的排放基本不变；贾崎[22]提出适当的预喷油量可以有效提高发动机的经济性，降低 NOx排放.Wang等[23]研究了过量空气系数对 NOx排放和 BSFC的影响，结果表明随着过量空气系数的不断增大，NOx排放与BSFC都不断减小，但当过量空气系数过高时，容易造成失火现象；天然气较高替代率可以使得燃烧产生的最高温度降低，减少 NOx的排放，但指示功率会下降，损失部分经济性[24].

综上分析，结合能够采集的发动机性能及排放数据，最终确定神经网络预测模型的输入参数为转速、转矩、轨压、主喷正时、预喷正时、预喷油量、过量空气系数和替代率，其中转速和转矩用来确定不同工况点，优化剩余6个控制参数来确定不同工况点最优的控制参数组合.输出参数为NOx排放和BSFC.

由于双燃料发动机的转矩下边界需要考虑能从柴油模式切换到双燃料模式的最小转矩即 300 N·m，而上边界则与柴油模式相似，为不同转速下对应的最大转矩，转矩随转速变化的外特下曲线如图2a所示.替代率的最大值受到引燃柴油量的限制，引燃柴油量必须大于最大预喷油量才能保证发动机的平稳运行，经过多次试验验证最大预喷油量为9mg/cyc.根据以上原则，计算替代率的边界范围如图2b所示，剩余参数的范围见表3.

表3 输入参数及范围Tab.3 Input parameters and ranges

图2 转矩和替代率边界Fig.2 Torque and substitution rate boundary

依据 V优化和空间填充相结合的试验设计原理对试验工况点进行设计，一共 600个试验点，在发动机试验台架上获取数据，每个测试点进行 100个循环，从这 100个循环里每隔 10个循环选取 1组数据，总共6000个时序数据参与神经网络训练.

2 基于LSTM神经网络的预测建模

2.1 LSTM神经网络简介

LSTM 是由 Hochreiter等为解决传统循环神经网络(RNN)存在梯度爆炸问题[25]而提出的一种改进的时间循环神经网络.相较于传统的RNN，LSTM的信息传递机制更加完善，可以更有效地提取时序数据中的关键信息，用于后续的时序预测，使得预测精度更高.LSTM的这一特性主要是由其在RNN的基础上加入了用于储存时序数据信息的细胞单元C，和用于删除或者增加信息到细胞单元 C的三个门结构，分别是遗忘门、输入门和输出门，LSTM 的神经元结构如图3所示.其中，xt为 t时刻网络的输入值；ht-1、ht分别为 t-1、t时刻 LSTM 神经元的输出；Ct-1、Ct分别为 t-1、t时刻 LSTM 神经元的细胞单元；σ为 sigmoid激活函数；tanh为 tanh激活函数；Wf、Wi、Wc和Wo分别是遗忘门、细胞单元、输入门和输出门的权重.具体计算步骤参见文献[26].

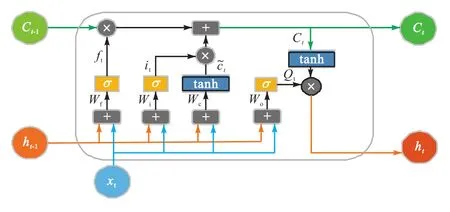
图3 LSTM的神经元结构Fig.3 Neuronal structure of LSTM

2.2 LSTM神经网络预测模型

由于实际输入参数的量级不同，为了避免数量级小的参数被数量级大的参数所掩盖，首先将输入/输出参数进行归一化处理，将参数归一到[-1，1]之间，表达式为

式中：x为待归一化的向量；xmax为样本最大值；xmin为样本最小值；x为归一化后的向量.

损失函数是网络训练的评价指标，网络训练的过程就是使损失函数最小化的过程，损失函数越小，说明网络训练越好，模型预测能力越强.通常使用均方根误差(RMSE)作为损失函数，表达式为

式中：n为预测序列长度；fi为模型预测值；yi为实际测量值.

神经网络的结构直接影响预测模型的性能，但隐藏层数目没有确切的理论依据，需要根据实际情况不断尝试、分析和总结得出.以模型最终预测值的RMSE作为网络结构好坏的评价指标.图4为综合两个输出目标的均方根误差，选用隐含层个数为8层.

图4 隐藏层数量与均方根误差Fig.4 Number of hidden layers and RMSE

神经网络的性能在很大程度上取决于其优化算法的选择，优化算法决定了神经网络权值校正、结构优化、收敛速度和损失函数值等.传统随机梯度下降SGD(stochastic gradient descent)优化算法对于非凸的误差函数容易陷入局部最优，采用自适应矩估计Adam(adaptive moment estimation)优化算法，根据梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率[27]，不仅能更有效地获得全局最优解，而且收敛速度更快，所建立模型的预测精度也更高[28-29].为了防止梯度爆炸，将梯度阈值设置为 1，指定初始学习率为0.02，在125轮训练后通过乘以因子0.2来降低学习率.

2.3 预测模型评价

选取 80%时序数据参与神经网络的训练，剩下的 20%用于模型预测能力的验证，训练后模型的预测能力采用统计度量决定系数 R2、RMSE、平均绝对误差(MAE)进行评价[30]见式(5).其中 R2是用来衡量被拟合数据在回归线上拟合优良的指标，R2越接近于1代表模型的拟合效果越好；RMSE和MAE都是用来描述预测值与真实值的误差，数值越小越好.

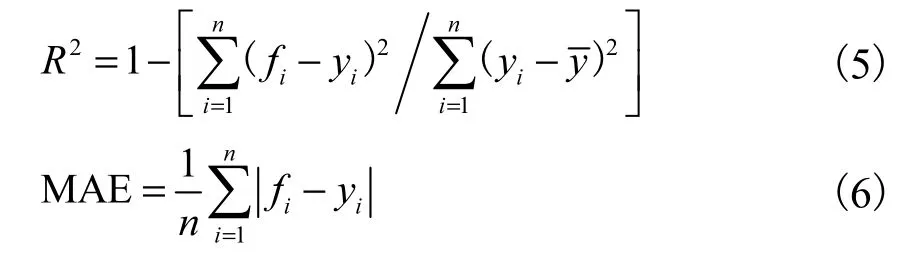
表4为神经网络性能统计值，通过对神经网络进行训练，其对未参加训练的测试集表现出良好的预测效果.图5所示试验值与预测值的分布都集中在y=x这条回归线附近，显示出良好的回归效果；且测试集的 NOx与 BSFC的决定系数 R2均在 0.98～1.00间，表明所建立的神经网络对目标输出参数具有良好的可预测性.

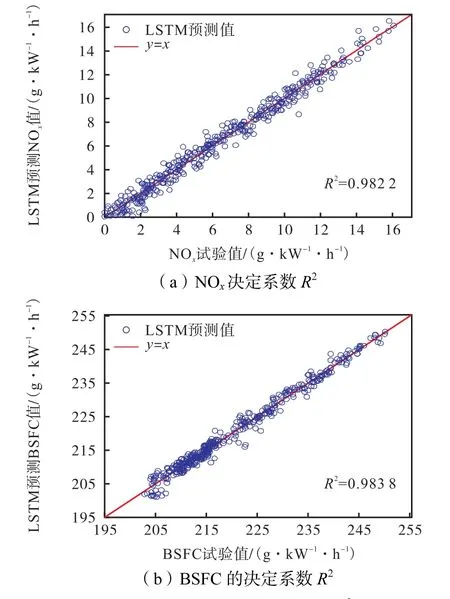
图5 测试集的决定系数R2Fig.5 Determination coefficient R2 of the test set

表4 神经网络性能统计值Tab.4 Statistical value of the performance of the networks

图6a为LSTM预测的NOx值与试验值的对比，整体的趋势基本一致，只在个别波动大的点预测值稍有偏差，根据计算测试集的 RMSE为 0.5396、MAE为0.4226，都处于其理想的范围，表明利用LSTM神经网络建立NOx预测模型是可靠且精确的.图6b为LSTM预测的BSFC值与试验值的对比，根据计算测试集的RMSE为1.5703、MAE为1.1797，也都处于理想的范围，表明利用 LSTM 神经网络建立 BSFC预测模型同样也是可靠且精确的.

图6 测试集的试验值与LSTM预测值对比Fig.6 Comparison of experimental values and LSTM predicted values of the test set

3 基于NSGA-Ⅱ算法的多目标优化

3.1 NSGA-Ⅱ算法简介

NSGA-Ⅱ算法不仅可以更好地保持种群的多样性，而且引入精英选择策略防止优秀个体被淘汰，同时具备遗传算法可以在整个解空间内搜索、获得全局最优解的能力，NSGA-Ⅱ的计算流程[18]如图7所示.首先通过非支配排序与拥挤距离计算这两个原则来评估每一代种群中更优秀的个体；其次通过选择、交叉和变异产生新的子代种群；然后利用精英策略，将每一代的父代与子代个体混合后再进行非支配排序与拥挤距离的计算；最后根据以上两个评估结果对种群进行修剪，反复进行这个过程直到达到最大的迭代次数.其中，Pi代表第 i代种群父代；Ci代表第 i代种群子代.

图7 NSGA-Ⅱ算法的计算流程Fig.7 Computational flow of NSGA-Ⅱalgorithm

3.2 多目标优化

为了解决双燃料发动机排放与燃油消耗之间难以调和的矛盾，以排放指标 NOx为目标一，以 BSFC为目标二，进行多目标优化，同时根据排放法规要求对排放指标CO与HC进行限制，建立数学模型为

式中：THC、TCO为排放法规标准限值；0.9为安全系数；X的各参数取值范围见表3；RP为轨压；MIT为主喷正时；PIT为预喷正时；PTQ为预喷油量；SRL为过量空气系数；EAC为替代率.

在基于 NSGA-Ⅱ算法进行发动机优化计算时，转速和转矩对应当前优化工况点的转速与转矩，不参与种群的生成，以LSTM预测模型的剩余6个控制参数为需要优化的种群个体.由于 NSGA-Ⅱ算法优化过程需要不断进行选择、交叉和变异生成新的子代种群，这样就要求不断计算相对应的目标输出值即种群的适应度值，如果直接使用真实的发动机或仿真计算模型，将需要耗费大量的时间，笔者提出使用 LSTM神经网络和 NSGA-Ⅱ算法进行联合运用，即利用LSTM 神经网络建立的发动机预测模型代替真实的发动机，快速输出每个种群个体相应的适应度值，然后利用 NSGA-Ⅱ算法不断进行迭代寻优，快速高效地寻找当前工况点控制参数的最优解集，具体流程如图8所示.首先 NSGA-Ⅱ算法固定当前工况的转速与转矩，随机产生 6个控制参数的种群，并将以上种群作为 LSTM 预测模型的输入；然后 LSTM 预测模型计算出每个种群个体相对应的目标输出值，并作为适应度值输入进 NSGA-Ⅱ算法；最后 NSGA-Ⅱ算法根据其原理评估当前种群中更优秀个体，反复进行这个过程直到达到NSGA-Ⅱ算法的最大迭代次数.

图8 LSTM神经网络和NSGA-Ⅱ算法联合运用示意Fig.8 Schematic diagram of combined application of LSTM neural network and NSGA-Ⅱ algorithm

由于对象为船用双燃料发动机，船舶发动机一般按照设定的推进特性工况运行，对推进特性曲线的每个发动机工况进行优化，并将优化后的结果与原机实际测得的结果进行比较分析，原机实际设定值见表5，推进特性下各转速所对应的转矩见表6.

表5 原机工况参数设置Tab.5 Initial working condition parameter setting

表6 双燃料发动机推进特性Tab.6 Dual-fuel engine propulsion characteristics

3.3 优化结果及分析

优化中设置种群大小为 100，通过记录每一次迭代优化后种群中最优解的个数来判断是否获得全局最优解.当 100个种群个体都在第一前沿时，说明寻优完成，当前解集即此工况下的全局最优解集.图9所示推进特性下 8个工况点在迭代 150步后 Pareto前沿面上最优解个数均达到 100，所以研究设置迭代步数为150步.

图9 迭代次数与最优解集个数Fig.9 Number of iterations and number of optimal solution sets

以推进工况 1(转速为 800r/min，转矩为 404 N·m)为例，绘制了其在迭代过程中的 Pareto前沿的解集情况，图10a显示了 NSGA-Ⅱ算法迭代 1次以后的 Pareto前沿的解集情况，可以看出一共有 13个前沿，但第一前沿只有 10个解，在迭代 150次以后见图10b，一共只有一个前沿，且这个前沿有 100个解，再次证明迭代 150次以后，可以获得当前工况下的全局最优解.

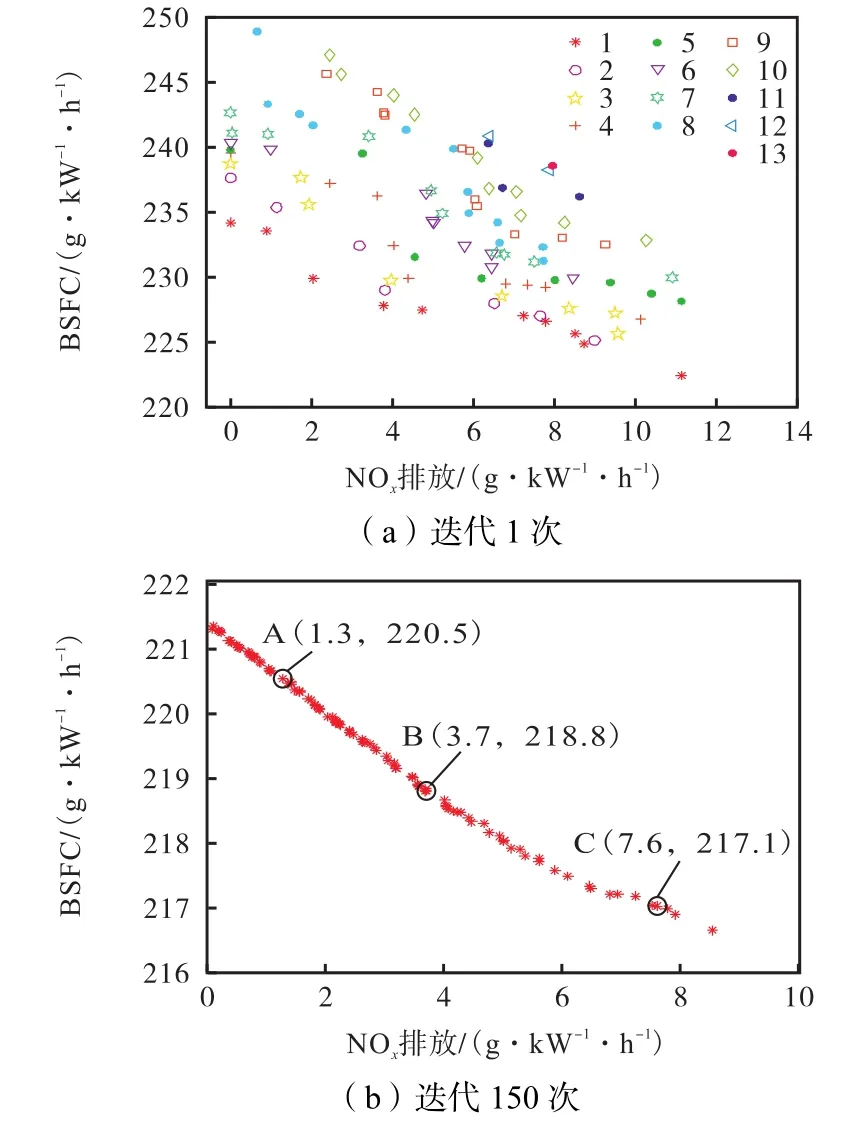
图10 Pareto前沿解集Fig.10 Pareto frontier solution set

获得全局最优解集后，可以根据自己的需求选择最适合自己目标的最优解，如果想要尽量减小NOx的排放，满足更高的排放法规要求，缓解环境污染问题，可以选择 A点附近的解；如果想要尽量提高双燃料发动机的经济性，可以选择C点附近的解；如果想要既改善 NOx的排放，又在一定程度上提高经济性，可以选择的是B点附近的解.为了满足IMO Tier-Ⅲ对船舶发动机排放污染物NOx排放的限制要求，选取A附近的点作为最优解，牺牲一部分经济性，来满足排放法规要求.按照这个原则，选取剩下 7个工况点的最优解，并记录其最优的控制参数组合如表7所示.

表7 推进特性下的最优控制参数组合Tab.7 Optimal control parameter combination under propulsion characteristics

3.4 配机验证

将优化得到的最优控制参数组合标定到发动机ECU上，完成配机试验.由于对工况进行逐个优化，所以得到的优化结果具有离散特性，需要对离散的优化结果进行处理，一般采用双三次多项式插值的方法，可以获得更平滑、精确的控制参数MAP图，以轨压MAP为例如图11所示.

图11 轨压MAP示意Fig.11 MAP figure of rail pressure

图12a为优化前、后 NOx值的试验结果对比，每个工况的 NOx都得到了良好的优化，根据计算相较于优化前，NOx排放平均下降了 76.4%；图12b为优化前、后BSFC值的试验结果对比，中、低转速BSFC较高时，优化的效果较好；高转速 BSFC较低时，保持 BSFC而降低 NOx的排放，根据计算相较于优化前BSFC平均下降了3.5%.

图12 优化前、后试验数据对比Fig.12 Comparison of experimental data before and after optimization

表8所示根据IMO Tier-Ⅲ对船舶发动机排放污染物 NOx排放的限制要求，所使用的柴油引燃天然气发动机，标定转速为1500r/min，对应的IMO Tier-Ⅲ排放限值为 2.08g/(kW·h).根据推进特性，进行4个工况试验，得到的结果见表9，通过加权计算，最终 NOx排放为 1.63g/(kW·h)，这个结果低于 IMO Tier-Ⅲ法规要求的21.63%.