基于机器学习的二次电子发射唯象模型

杨文晋，李永东，曹 猛，王洪广，刘纯亮

(西安交通大学 电子物理与器件教育部重点实验室 电子与信息学部电子科学与工程学院，西安 710049)

0 引言

二次电子发射是指电子或离子轰击材料表面，引发电子从材料表面逸出的现象。在航天大功率微波器件中，二次电子发射可能引发电子倍增，进而产生微放电，导致器件烧蚀或击穿[1-4]。因此，在航天微波器件的设计过程中，针对器件微放电阈值的研究非常重要。考虑到实验成本较高且设计周期较长的缺点，一般会首先基于理论分析和数值模拟开展微放电阈值研究[5-8]。在微放电数值模拟中，得到用于描述材料二次电子发射特性的数值模型至关重要。已有研究成果表明，材料二次电子发射特性对微放电阈值影响巨大[9-11]。另外，更精确的二次电子发射模型还可以应用于沿面闪络、加速器、光电倍增管等二次电子倍增问题的研究中。因此，建立精度更高的二次电子发射模型是很有必要的。

在开展二次电子发射相关的数值模拟研究前，一般需要先利用实验手段测量材料真实的二次电子发射特性。然后，参照实验结果对已有理论公式进行参数修正，用于描述材料真实的二次电子发射特性。较为常用的二次电子发射模型有Vaughan、Furman、复合唯象模型等[12-14]。

但是，受理论公式可调参数的限制，仅通过修正公式参数，无法确保模型与实验数据完全匹配，且参数修正过程复杂繁琐。同时，受限于实验条件、实验成本和实验精度等，实验测试得到的材料二次电子发射特性是强离散的，这种离散的实验数据会导致部分物理规律缺失。因此，如果抛弃理论公式，仅针对实验数据进行拟合，则容易产生过拟合现象，导致生成的拟合公式缺乏普适性，甚至产生非物理错误。

本文基于机器学习和深度人工神经网络，提出了一种二次电子发射唯象模型及分步训练的方法。针对银和铝合金材料的测试结果表明，本文提出的基于机器学习的二次电子发射唯象模型较Vaughan模型、Furman模型和复合唯象模型均能够更好地描述材料真实的二次电子发射特性。

1 Vaughan模型

Vaughan模型[12]是一种经典的二次电子发射唯象模型，该模型描述的二次电子发射系数(secondary emission yield，SEY)为：

(1)

其中δmax0是电子垂直入射时的最大SEY，ks是材料表面光滑度因子，f(w,k)为基于经验参数的拟合函数。

(2)

(3)

本文利用Vaughan模型生成先验知识数据集，用于训练二次电子发射ANN模型，生成二次电子发射先验知识ANN模型。

2 二次电子发射ANN模型

本文提出的二次电子发射ANN模型指利用人工神经网络描述材料二次电子发射特性的唯象模型。

近年来，新的人工神经网络模型不断被提出，如用于图像分类的AlexNet、VGGNet、GoogleNet、ResNet等[15-18]；用于目标检测的R-CNN、YOLO、SSD等[19-21]；用于图像区域分割的FCN、DeepLab、PSPNet等[22-24]；用于OCR识别的CTPN、CRNN等[25-26]；用于语音识别的DNN-HMM、RNN-CTC、FSMN、LSTM-DNN等[27-31]。由于二次电子发射建模问题较上述应用场景包含的信息量少，不适于使用复杂的人工神经网络结构。因此，本文提出的ANN模型是一种由输入层、5层隐含层和输出层组成的全连接人工神经网络。二次电子发射ANN模型的网络结构如图1所示。神经网络的输入参数为入射能量(E)、入射角度(θ)、垂直入射时最大SEY(δmax0)和δmax0对应的电子入射能量(Emax0)，输出结果为SEYδ(E,θ)，神经元激励函数为Relu函数。

图1 二次电子发射ANN模型Fig.1 SEY ANN model

针对二次电子发射ANN模型采用分步训练方法。首先，利用经过预先验证的二次电子发射特性数据作为样本集训练神经网络，生成二次电子发射先验知识ANN模型，用于描述二次电子发射一般规律。然后，利用实验测得的某种材料的SEY实验数据作为样本集，对二次电子发射先验知识ANN模型进行二次训练，生成针对该材料的特异ANN模型。上述特异ANN模型用于描述具体材料的二次电子发射特性，是二次电子发射ANN模型的具象化实例。

分步训练方式将先验知识预先引入模型，在确保模型与实验数据拟合精度的前提下，提高了二次电子发射ANN模型对小样本的适应性，同时避免了只针对实验数据进行拟合而可能导致的过拟合现象。

2.1 先验知识ANN模型

先验知识ANN模型指利用预先验证的二次电子发射特性数据作为训练集，训练二次电子发射ANN模型，生成的一种隐含了二次电子发射一般规律的ANN模型。

本文利用Vaughan模型生成二次电子发射特性先验数据集，集合形式如式(4)所示：

{Ein,θin,δmax0,Emax0,δ}

(4)

其中Ein为电子入射能量，θin为电子入射角度，δmax0为电子垂直入射时最大SEY，Emax0为δmax0对应的电子入射能量，δ为利用Vaughan模型计算得到的SEY。参数取值范围如式(5)所示。

(5)

本文在参数取值范围内采用均匀采样方式生成包含2 000万组数据的样本集。其中，用于训练和测试的样本数量比例为7:3。

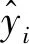
(6)

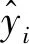
(7)

模型训练收敛判据为：

(8)

先验知识模型训练收敛过程如图2所示。其中，横轴为训练迭代次数，纵轴为损失函数，Train MSE代表训练数据集的损失函数变化，Test MSE代表测试数据集的损失函数变化。

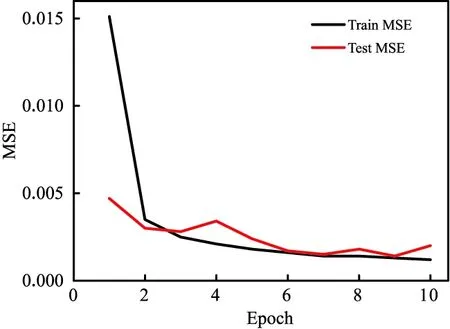
图2 训练收敛结果Fig.2 Training convergence result(color online)

在不同参数条件下(详见图题内容)，Vaughan模型与二次电子发射先验知识ANN模型的对比结果如图3所示。其中，横轴为电子入射能量，纵轴为SEY，图例中ANN Model为先验知识ANN模型的计算结果，Vaughan为Vaughan模型的计算结果。

图3 ANN模型计算结果Fig.3 Prediction results of ANN model(color online)

上述验证结果表明，先验知识ANN模型在不同参数条件下均能很好地拟合Vaughan模型。为了进一步提升先验知识ANN模型的性能，还可以利用Furman模型、复合唯象模型、实验数据等扩充先验知识数据集，训练生成综合性能更优的先验知识ANN模型。

2.2 特异ANN模型

二次电子发射特异ANN模型是指利用某种具体材料的真实二次电子发射特性数据作为训练集，对先验知识ANN模型进行二次训练，生成的一种仅用于描述该材料的二次电子发射模型。由于影响材料二次电子发射特性的因素非常多，仅利用上述先验知识ANN模型不能准确描述待研究具体材料的真实二次电子发射特性，因此，提出二次电子发射特异ANN模型是必要的。

利用文献[14]中银材料SEY实验数据修正先验知识ANN模型，生成针对该种银材料的特异ANN模型。银材料SEY实验数据共有120组，模型训练方法、参数设置及收敛条件同先验知识ANN模型。

特异ANN模型的训练收敛过程如图4所示。其中，横轴为训练迭代次数，纵轴为损失函数变化趋势，损失函数为MSE。

图4 训练收敛结果Fig.4 Training convergence

将该特异ANN模型与文献[14]中的修正Vaughan模型、修正Furman模型、复合唯象模型和实验数据进行对比，结果如图5所示。其中，横轴代表电子入射能量，纵轴代表SEY。图5中图例所示分别代表特异ANN模型计算结果、复合唯象模型计算结果、修正Furman模型计算结果、修正Vaughan模型计算结果和实验结果。

4种模型与银材料SEY实验数据对比的平均绝对误差(mean absdute error,MAE)结果如表1所列。ANN模型的MAE相对于Vaughan模型、Furman模型和复合唯象模型分别平均降低了84.1%、74.8%和62.1%。

表1 二次电子发射模型MAE对比结果(银)Tab.1 Comparison of SEY models MAE for silver

利用文献[14]中铝合金材料SEY实验数据修正先验知识ANN模型，生成针对该铝合金材料的特异ANN模型。铝合金材料SEY实验数据共有114组，模型训练方法、参数设置及收敛条件同先验知识ANN模型。

将该特异ANN模型与文献[14]中的修正Vaughan模型、修正Furman模型、复合唯象模型和实验数据进行对比，结果如图6所示。其中，横轴代表电子入射能量，纵轴代表SEY，图例意义同图5。

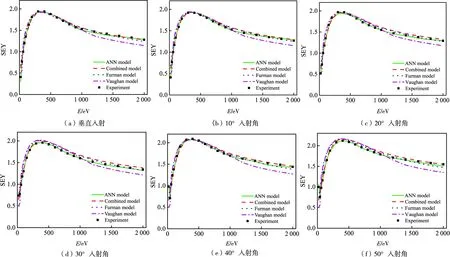
图5 二次电子发射模型对比(银)Fig.5 Comparison of SEY models for silver(color online)

图6 二次电子发射模型对比(铝合金)Fig.6 Comparison of SEY models for aluminum alloy(color online)

4种模型与铝合金材料SEY实验数据对比的MAE结果如表2所列。ANN模型的MAE相对于Vaughan模型、Furman模型和复合唯象模型分别平均降低了78.8%、32.5%和-0.7%。

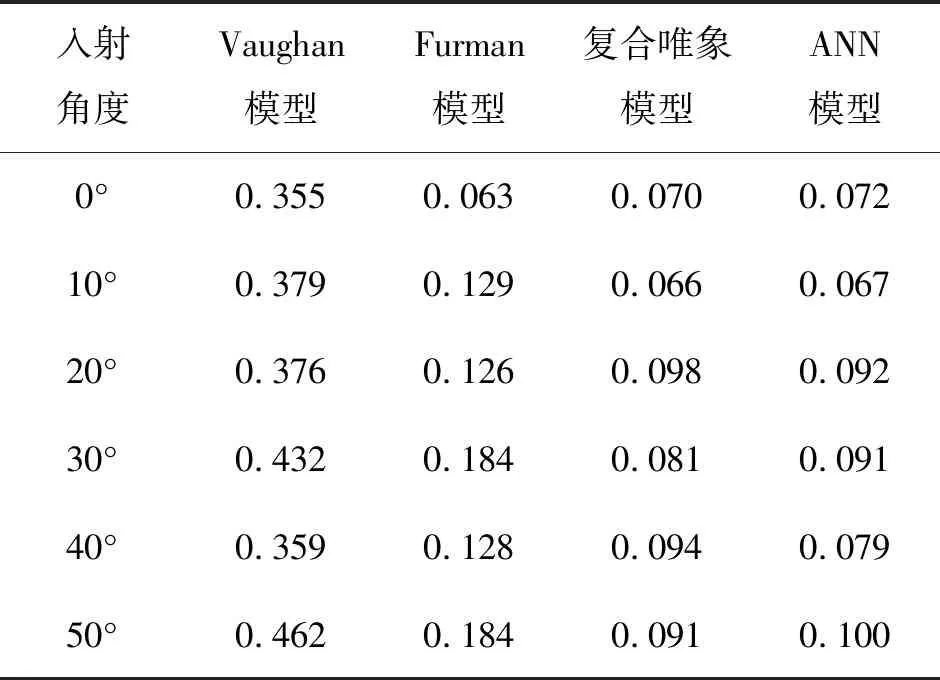
表2 二次电子发射模型MAE对比结果(铝合金)Tab.2 Comparison of SEY models MAE for aluminum alloy

2.3 小样本测试

本文提出的二次电子发射ANN模型是基于机器学习生成的，因此其准确性与样本数量强相关。本文结合文献[14]中的银材料实验数据，进一步测试了在小样本条件下，二次电子发射模型的准确性。

只选取电子垂直入射时银材料的20组SEY实验数据作为样本集，用于训练ANN先验知识模型，生成针对该种银材料的特异ANN模型，模型训练方法、参数设置及收敛条件同先验知识ANN模型。

由于缺少不同角度入射的SEY实验数据，不适于使用Furman模型和复合唯象模型。因此，在小样本条件下仅对比特异ANN模型与Vaughan模型，结果如图7所示。其中，横轴代表电子入射能量，纵轴代表SEY，图7中图例所示分别代表特异ANN模型计算结果、修正Vaughan模型计算结果和实验结果。

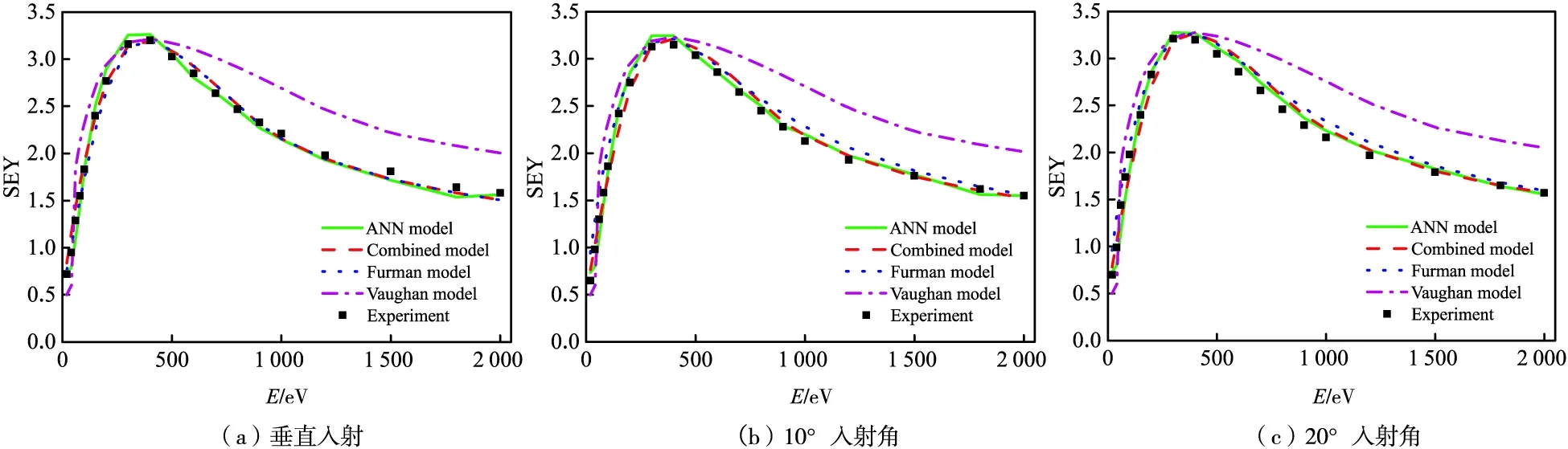
图7 二次电子发射模型对比(银)Fig.7 Comparison of SEY models for silver(color online)

两种模型与银材料SEY实验数据对比的MAE结果如表3所列。通过与表1结果进行对比可得出结论，当训练样本减少时，二次电子发射ANN模型的准确度下降，但相比于Vaughan模型依然获得了相当或更高的精度。ANN模型的MAE相对于Vaughan模型平均降低了32.2%。

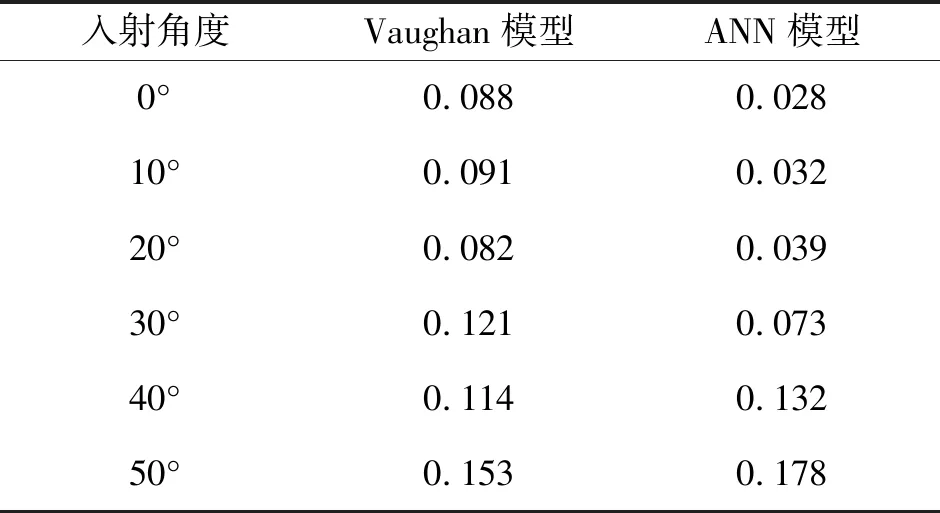
表3 二次电子发射模型MAE对比结果(银)Tab.3 Comparison of SEY models MAE for silver

3 结论

本文基于机器学习和深度人工神经网络，提出了一种参数易修正，且精度更高的二次电子发射唯象模型。在针对该模型的训练过程中，采用分步训练方式先后生成先验知识ANN模型和特异ANN模型。

在不同参数条件下比对了先验知识ANN模型和Vaughan模型，验证了先验知识ANN模型的正确性。分别利用银和铝合金材料的实验数据修正先验知识ANN模型，生成针对两种材料的特异ANN模型，并通过与修正后的Vaughan模型、Furman模型和复合唯象模型进行对比，验证了特异ANN模型的准确性。在小样本条件下，对比了特异ANN模型和Vaughan模型，验证了二次电子发射ANN模型对于小样本的适应性。

二次电子发射ANN模型的优势不仅体现在与实验数据的拟合精度上，而且体现在模型使用方面。二次电子发射ANN模型的训练方法具有普适性，无需人为过多干预。避免了传统方法需要人为主观进行参数修正的繁琐过程，且对于小样本情况适应性较好，更适于在数值模拟中使用。

在下一步的研究工作中，拟利用Furman模型、复合唯象模型和高能二次电子发射模型[33]扩充先验知识训练数据集，用于训练性能更优的先验知识ANN模型。然后，拟将基于机器学习的二次电子发射唯象模型应用于粒子模拟微放电阈值计算中，进一步验证该模型的正确性和优势。