不规则波在孔隙介质礁坪上传播过程的波高和增水变化数值研究
2022-09-25何栋彬马玉祥董国海
何栋彬,马玉祥*,董国海
( 1. 大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
1 引言
自然条件的岛礁地形上孔隙介质相当常见,块状的岩石、珊瑚骨骼结构乃至植被,都可以视为孔隙介质;在人工岛礁或者防波堤等工程结构中,也往往采用孔隙介质来减弱波浪的冲刷,从而起到保护海工建筑物的作用。然而孔隙介质的影响在以往的数值模型中往往被忽略,或者使用一个包含拖曳力系数Cd和速度平方项的关系式来进行处理[1-3],这种方式较为简单但比较粗糙。近些年来,使用体积平均的雷诺时间平均(Volume-Averaged Reynold-Averaged Navier-Stokes, VARANS)方程来处理孔隙介质中的流动问题[4],由于其没有引入静压假定、缓坡假定等近似假设,并完整保留了垂向动量方程,对各类地形水深条件不存在限制,适用于复杂水波运动,正受到越来越多的关注。
孔隙介质中存在流体时,被认为是一种包含固体和液体的两相介质,通常假设为刚性的,内部空腔互相连通[5]。孔隙介质的一大特征是其内部空腔的形状、大小不规则,且分布无规律,所以模拟孔隙内部每一个流体质点的运动情况是不现实的,也是没有必要的。VARANS模型的解决思路是对包含孔隙介质的流动区域在空间上进行体积平均,通过平均化的光滑效果,将孔隙介质的空间不均匀性所导致的小尺度波动过滤掉,类似于雷诺平均方法处理湍流问题。VARANS方程与雷诺时间平均(Reynold-Averaged Navier-Stokes, RANS)方程通过孔隙率(孔隙介质内部空腔的体积占比)相联系,可采用同一形式表达,统一了孔隙介质内部和纯流体区域的流动方程形式,即在孔隙介质内部,流动方程为VARANS方程,但在孔隙介质外部,VARANS方程自动转换为RANS方程。经过体积平均后的RANS方程需要有相关的封闭项对方程进行封闭,经过多年的发展,现在基本采用经过扩展的Forchheimer关系式,该表达式首先由Forchheimer提出,即在原始的Darcy公式的基础上,加入考虑湍流运动的阻力项[6],后续Polubarinova-Kochina[7]又加入了包括附加质量系数的时间偏导数项来考虑流体的非定常流动效应,其中的各项系数经过大量的研究和校正[8],目前取值已趋于固定,并得到了较为广泛的验证[9-12]。另外,对于VARANS方程中的湍流耗散项,体积平均后也需要对相应的湍流模型进行处理,目前由Nakayama和Kuwahara[13]建立的体积平均的k-ε模型是最常用的。
在多种水波数值模型中,非静压模型由于其将自由表面处理为单值函数,简化了追踪自由表面的难度并提升了计算效率,同时保持了很高的精度,在许多复杂的水波问题中都得到了很好的验证和应用[14-17],而非静压模型一般以N-S方程或者RANS方程作为控制方程,因此将VARANS方程与非静压模型相结合是非常自然的。综上,本文基于VARANS方程建立了非静压水波模型,可用于模拟岛礁地形大粗糙度或类孔隙结构对波浪传播运动的影响。通过与相应物理模型实验的对比,以证实在数值模拟中将地形粗糙单元/结构等效为孔隙介质进行计算这一方法的有效性,并研究分析岛礁地形表面大粗糙度(孔隙介质)对礁坪上波高和平均水位变化的影响。
2 基于VARANS方程的非静压模型
2.1 控制方程
非静压模型的一大特点是将自由表面处理成单值函数,从而可以在水面和水底建立贴体网格体系,大大简化自由表面的捕捉难度并提高计算效率。其中一种方法是将原本建立在直角坐标系(x*,y*,z*)中的控制方程转化到σ坐标系(x,y,σ)下,相应的σ=1,0分别表示自由表面和水底。将这一转换过程用于VARANS方程,在σ坐标系下的守恒形式控制方程可表达为
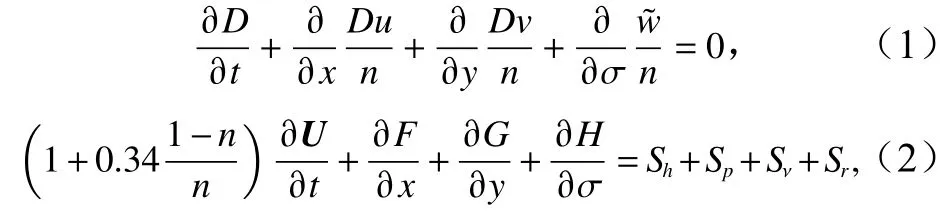
式中,n表示孔隙率,定义为孔隙介质内部一定体积范围内空腔的占比,当n=1时,式(1)和式(2)即退化为RANS方程;D为总水深,为静水深(h)和波面高程(η)之和,即D=h+η;U=(Du,Dv,Dw)T,为守恒变量;F、G、H为通量项;Sh表示与水底地形变化相关的底坡源项;Sp表示由水面波动引发的动压力项;Sν表示湍流耗散项,使用体积平均后的k-ε模型计算湍流[13];u,v,为σ坐标系下的水质点速度;且与直角坐标系下的垂向速度w存在下述关系:
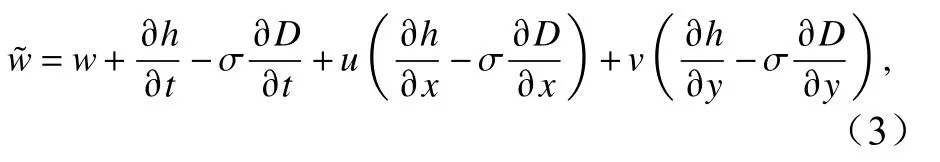
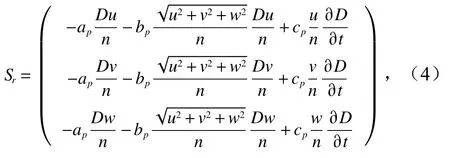
上述各项的具体表达形式可以参考文献[10,18]。式(2)中Sr即为描述孔隙介质对流体运动影响的相关项,来源于拓展的Forchheimer关系式,用于封闭体积平均后的RANS动量方程,具体表达式为上式右侧每一方向的分量中,第一项为线性项,表示层流状态下由多孔介质施加的摩擦力;第二项为速度的二次方项,表示湍流运动产生的摩擦力;第三项来源于表示惯性力作用(附加质量)的时间导数项,用以描述流动的非定常状态。各项对应的系数如下所示:

式中,D50表示多孔介质的中值粒径;γ是和附加质量相关的经验系数,通常取0.34;Keulegan-Carpenter系数表示流体水质点运动的特征长度与孔隙介质特征长度的比值[11],即,其中T为波浪周期。另外,参考Ma等[10]的推荐取值,本文计算取α=200,β=1.1。
与其他采用贴体网格系统的非静压模型不同,为了保持边界条件的连续性,本文并不忽略在自由表面和水底处的切向应力,参考Derakhti等[19]的工作,当水面无风力作用时,对切向方向的速度边界条件作出如下修正:
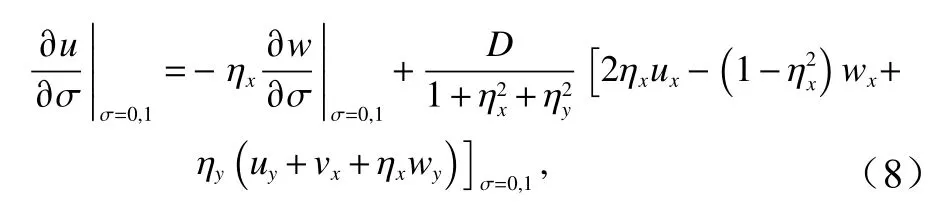
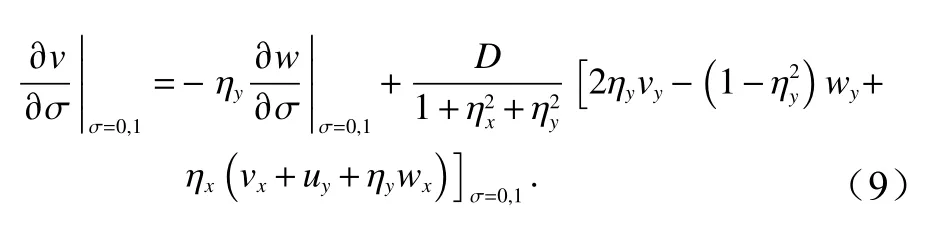
2.2 数值格式
采用有限体积和有限差分混合格式离散方程,并参照He等[18]建立的非静压水波数值模型,采用三阶中心加权无振荡格式来对单元网格边界面上的守恒变量进行重构,并使用MUSTA格式计算相应的数值通量,从而建立了Godunov类型的高精度间断捕捉格式以处理波浪破碎问题。时间步进上采用二阶Runge-Kutta方法,并结合显式的预估-校正格式计算动压力以修正速度场。
3 数值计算设置与网格收敛性分析
3.1 数值计算地形参数
本文的数值计算参考Buckley等[20]在粗糙(孔隙介质)底床上开展的物理模型实验进行设置。物理模型实验的水槽长度为55.0 m,对于数值模拟,为了避免波浪在造波位置出现二次反射,采用域内造波的方式生成波浪,所以相比于模型实验,水槽在左端增加5.0 m以方便设置造波源和海绵阻尼层(图1)。造波源距离礁前斜坡坡脚25.5 m,礁前斜坡坡度为1∶5,后接礁坪段长14.0 m,距地面高程为0.7 m,礁坪段末端设置有1∶12的斜坡。图1中黄黑色虚线段标注的区域表示设置孔隙材料的区域,在相应的物理模型实验中,使用了边长为1.8 cm的混泥土立方块来模拟自然条件下礁坪上的粗糙度,这种方法常用于在物理模型实验中模拟底部粗糙度[21-22]、植被等[23-24],也可以用于模拟孔隙材料。在本文的数值计算中,参考物理实验设置进行换算,在礁前斜坡和礁坪上方相同的区域,设置了孔隙率为0.87,中值粒径为1.8 cm,高度为2.0 cm的孔隙层材料。
另外,根据模型实验设置,数值计算域沿程设置了17个波面高程测点(波面以下为负值),各测点坐标位置从左到右依次为-15.0 m、-5.3 m、-3.0 m、-2.0 m、-1.0 m、-0.5 m、0 m、0.34 m、1.0 m、1.6 m、3.0 m、4.2 m、5.8 m、7.5 m、9.0 m和11.0 m。
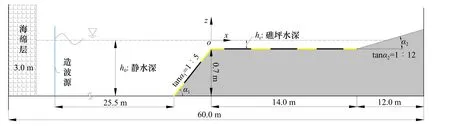
图1 礁坪地形及计算域布置示意图Fig. 1 Schematic of the reef flat and the computational domain layout
3.2 波浪和水位参数
为研究在不同波浪和水位条件下,孔隙介质对礁坪上方波高和增减水的影响是否存在某些共性,因此,在数值计算中一共设置了16个不同的波浪条件和水位组合,其中每一个组合又都包括光滑底床和孔隙底床两种设置,总计32个工况。域内造波使用Bouws等[25]提出的TMA谱生成波面时间序列,表中的波高为均方波高Hrms。
3.3 网格收敛性分析
本文计算的岛礁地形属于二维剖面,为确定水平x方向的网格尺寸和垂向分层数,本小节对相应方向的网格收敛性进行分析。非静压模型能够通过增加垂向分层数来提高色散性能,有研究认为,有限水深下垂向取3~8层即可满足精度要求,而水平网格间距应不小于波长的1/40,否则会产生明显的波幅沿程衰减[10]。本节以表1中的组合1工况(谱峰周期对应的波长为5.5 m)为基础,设置不同的水平网格大小和垂向分层数,计算沿程各测点波面时间历程数据的差异性。设置两组网格参数:(1)保持垂向分层数为8层不变,调整x方向空间步长为0.08 m、0.06 m、0.04 m、0.02 m和0.01 m;(2)保持x方向空间步长为0.01 m不变,调整垂向分层数为2、4、6、8、10,本文所有计算中的垂向分层皆为均匀等间距划分。另外,为了量化不同网格参数下计算结果的差异性,引入Willmott[26]提出的统计模型:
由图7可知,随着硫酸盐干湿循环作用的增多,试件的相对动弹性模量先提高后降低,并在60次硫酸盐干湿循环作用处于最高值。原因是侵入混凝土内部的硫酸盐会与混凝土结晶反应生成石膏等。在较少次数的循环作用下,石膏等表现出的填充作用可以增加混凝土的密实度,故增大了动弹性模量;随后由于石膏等含量的增多,其表现出的膨胀作用增强,加快了试件内部裂缝的发展,破坏了混凝土的孔隙结构,故动弹性模量值随之降低[15-17]。
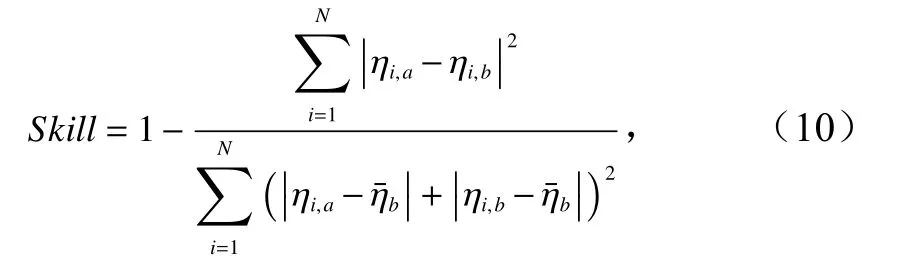
式中,Skill代表两个数据样本的相似度;a和b表示不同网格参数的波面数据;ηi,a和 ηi,b分别表示a、b网格参数对应的第i个时刻波面高程;表示网格参数b对应的波面时间序列平均值。另外, 0≤Skill≤1,Skill=1表示两个波面数据完全一致,等于0则表示差异最大。计算不同网格参数下,沿程各测点波面的Skill值,如图2所示。
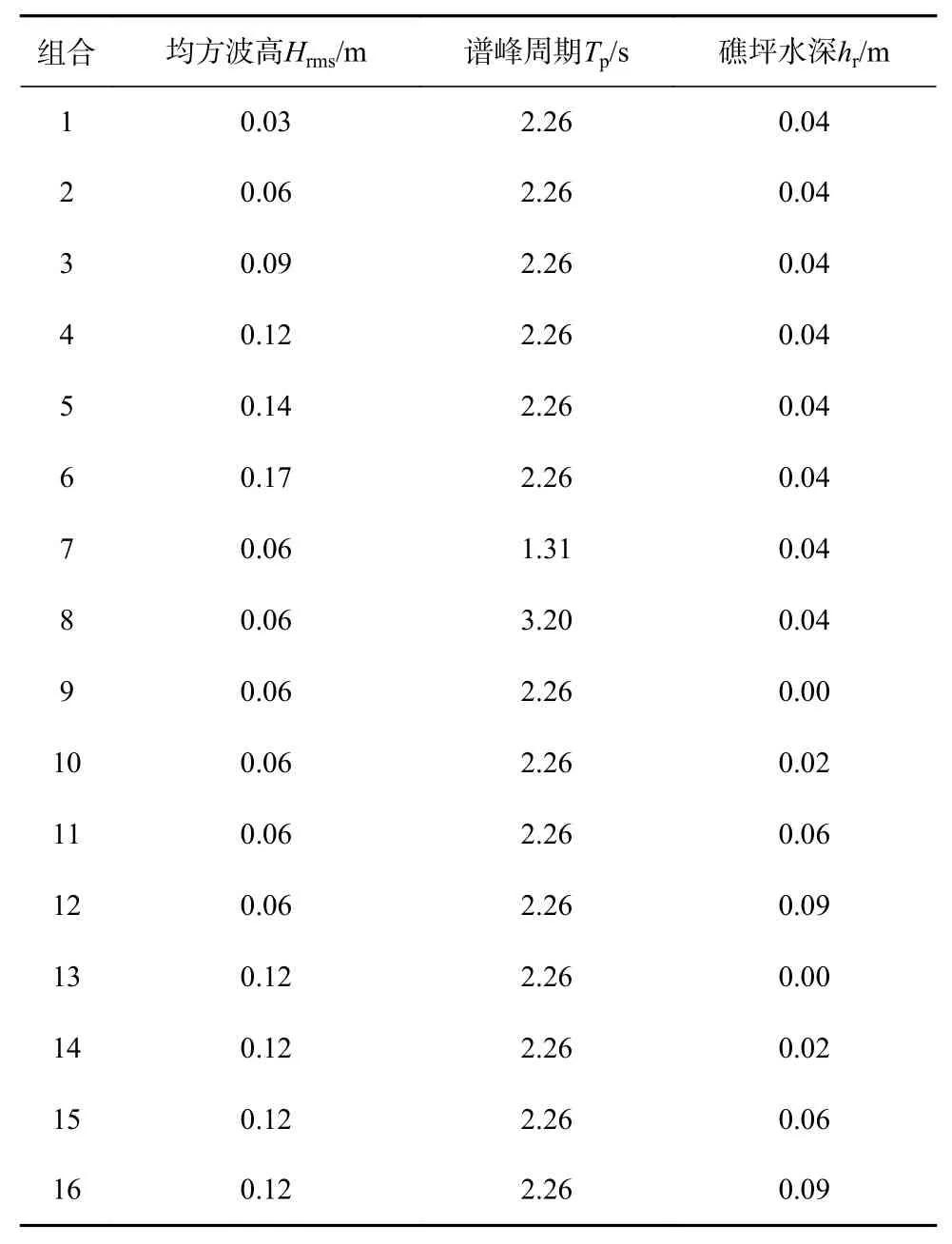
表1 数值实验波浪和水位参数Table 1 Parameters of wave and water level for the numerical experiments
可以看出,对于x方向不同的网格间距,在礁坪地形前方的常水深处波面差异很小,到达礁前斜坡后随着波浪的浅化变形,波面差异增大,进入礁坪区域后差异最为明显,Δx为0.08 m和0.06 m时礁坪处的Skill值约为0.95,但随着网格的加密,差异减小,Δx为0.02 m和0.01 m的Skill值已非常接近1,可以判断进一步加密网格不会对计算结果造成影响。而对于不同的垂向分层数,也有着相类似的结果,垂向均匀划分8层和10层,计算结果间的差别非常小,可以认为垂向分层数超过8时已能获得很好的收敛效果。
根据上述收敛性分析,在数值计算中,计算域沿x方向离散为6 000个网格,即网格间距取 Δx=0.01 m,垂向均匀划分10层,计算时间步长由Courant-Friedrichs-Lewy (CFL)条件控制。
4 结果与讨论
使用本文建立的基于VARANS方程的非静压水波模型,对表1中的16组波浪和水位参数分别在光滑和孔隙地形上的传播进行了模拟。下面以组合4的计算结果为例进行分析,对应的均方波高为0.12 m,谱峰周期为2.26 s,礁坪水深为0.04 m。

图2 水平方向网格间距(a)和垂向分层数(b)收敛性分析及地形剖面(c)示意图Fig. 2 Convergence of grid spacing in horizontal (a) and vertical direction (b) and the sketch of terrain profile (c)
图3中给出光滑底床和孔隙底床下,离岸处、礁前斜坡顶点和礁坪段的波面时间序列对比,即分别对应x为-15.0 m、0 m和6.0 m。显然,孔隙底床的存在并没有对波浪在礁坪地形上的传播形态造成明显变化,无论底床光滑与否,呈现出来的都是一个非常典型的简单斜坡-礁坪地形上波浪的传播变形过程。波浪从外海(造波源)传播到礁前斜坡上,由于斜坡对波浪的浅化作用,波形变陡,波高增大,最终在礁坪边缘附近发生破碎,如图3b所示,此位置处的波面时间历程线基本位于0水位线以上,表明在该位置处平均水位上升,即波浪增水。图3c中测点位于礁坪段,礁坪上水深极浅,由于波能的衰减,波浪形态从曲线上看变现为波高下降明显,波面历程线变得相对平坦,“起伏”程度变缓,同时波面过程线完全位于0水位线上方,表明礁坪上方出现了明显的增水,这可能是礁坪上方波浪高频成分耗散,低频成分有所增长在波形上的一种体现。
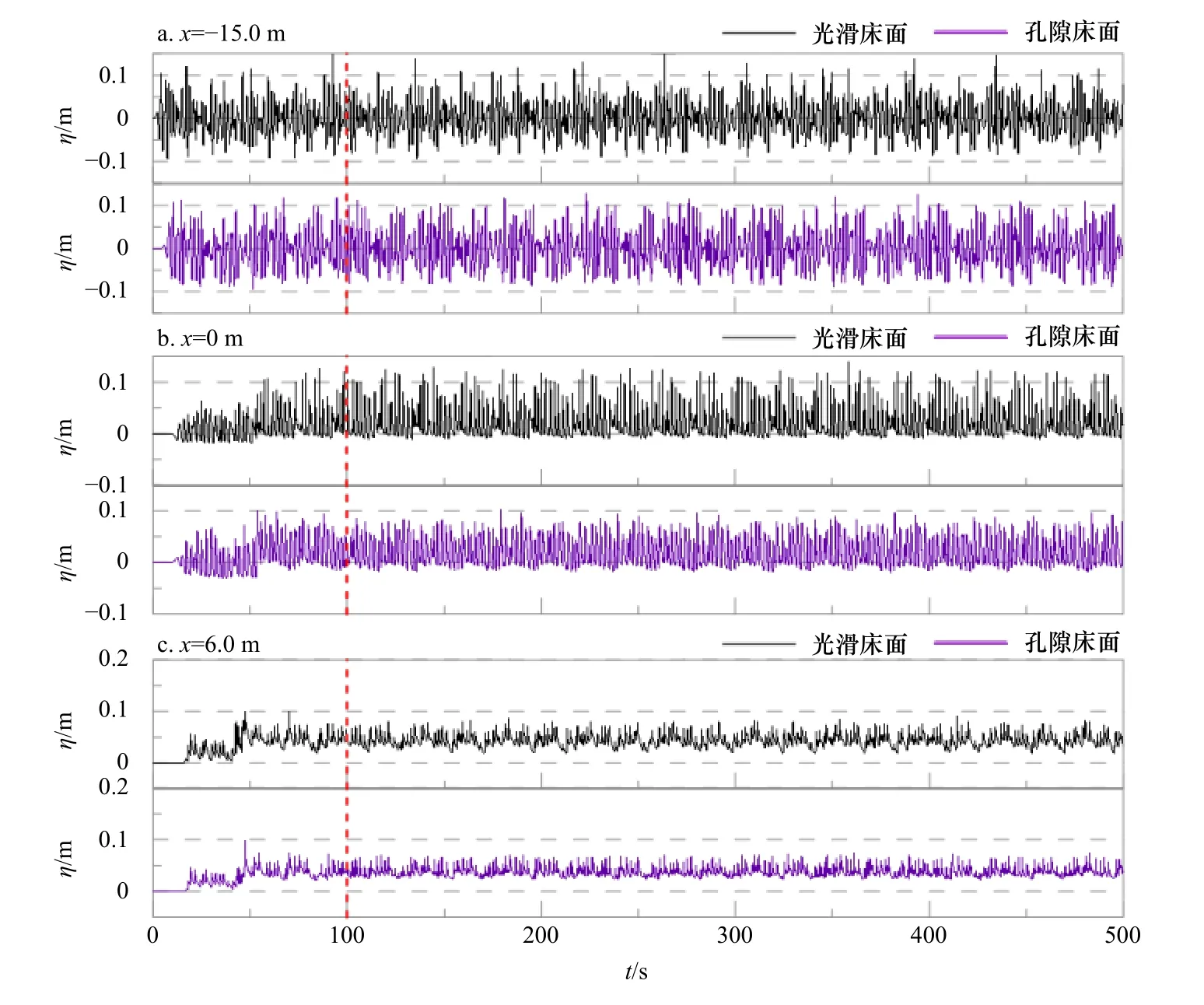
图3 组合 4测点波面高程历程曲线Fig. 3 Time series of simulated wave surface elevation for the Case 4
从图3中可以看出t=100 s以后的波浪趋于稳定,所以选取组合4工况t为100~500 s(图3中红色虚线处截断)时的波面数据分析均方波高和平均水位(物理实验中使用的数据时间长度为410 s),如图4所示。通过和物理模型实验的测量数据对比,无论是光滑床面还是孔隙床面,可以发现本文模型的计算结果与测量值保持了高度的一致,因此可以认为本研究建立的基于VARANS方程的非静压模型可以很好地模拟不规则波在典型礁坪地形上的传播。对于波高变化,图3所反映出来的变化与图2中的波浪形态基本是一致的,即离岸处基本保持稳定,经过斜坡浅化增大,在x=0附近发生破碎;与之对应的是平均水位在岛礁地形前方基本为0,在礁坪边缘前方出现平均水位的下降,但随后平均水位迅速升高,在礁坪上方体现为波浪增水,同时增水幅值沿礁坪向岸基本不变。
由于岛礁前方的深水区域不存在孔隙介质,所以波高和平均水位对于两种底床都基本一致。但对于孔隙床面,礁前斜坡和礁坪上方的波高都比光滑床面时有所下降,这是由于孔隙介质的存在加大了波浪能量的衰减。对于平均水位而言,孔隙床面情况下的最大减水幅值小于光滑床面,但礁坪上方的波浪增水两个床面则很接近,事实上,从实验测量数据上看,个别测点的数据甚至是重合的,说明对于光滑和孔隙两种底床,礁坪上方的增水幅值并不存在明显差别。
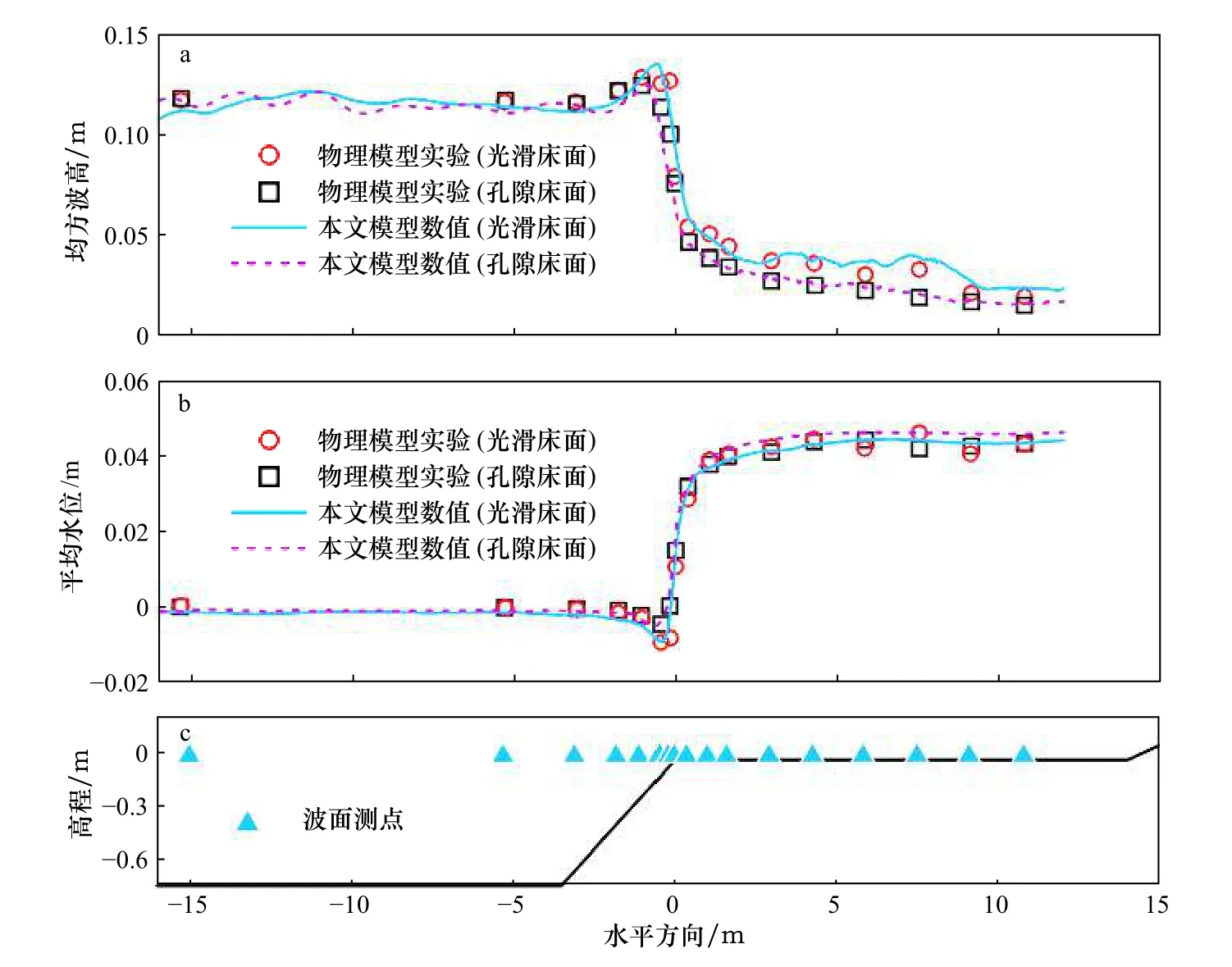
图4 组合 4光滑和孔隙底床下均方波高(a)、平均水位(b)和地形剖面(c)沿程变化Fig. 4 Mean square wave height (a) , mean water level (b), and terrain profile (c) for the Case 4 at porous and smooth beds

图5 孔隙底床和光滑底床在不同区域处均方波高的比较Fig. 5 Comparisons of the mean square wave heights at different regions for the porous and smooth beds
在礁坪上方,各实验组次对应的均方波高与水深的比值(Hrms/h)如图6所示。从图中可以看出在孔隙介质存在的情况下,礁坪上方的波高要小于光滑底床。图6中同时给出了本文模型数值计算结果和物理模型实验测量数据的对比情况,显然,数值计算给出的礁坪上方波高值要略大于实验测量,但二者的拟合直线(最小二乘法拟合)斜率是接近的。对于数值计算结果,孔隙底床条件下礁坪上方的波高水深比大约为0.4,光滑底床的平均值约为0.3;相应的实验测量数据则分别为0.36和0.27。
相比于波高的变化,孔隙介质对于平均水位的影响则有所不同。如图4b所示,各工况在礁坪前方出现最大减水,而光滑底床的减水幅值(绝对值)要大于孔隙底床,表现为图7中的数据点都位于1∶1斜率直线的上方,对于所有工况,本文模型数值计算结果显示二者比值的平均值为1.8,物理实验测量的平均值为1.7。
但是在礁坪上方,平均水位沿空间变化很小,同时平均水位基本一致,无论是数值计算还是实验测量结果,都反映了这一特点,如图8所示,数据点基本都分布在1∶1斜率直线上。采用最小二乘法进行拟合,可以发现数值计算结果的拟合直线斜率为0.98,实验数据对应的斜率为0.94。

图6 孔隙底床和光滑底床在礁坪上方均方波高和水深比(Hrms/h)Fig. 6 Comparisons of the ratio of mean square wave height to water depth (Hrms/h) on the reef flat for the porous and smooth beds

图7 孔隙底床和光滑底床条件下最大减水对比Fig. 7 Comparisons of maximum setdown for the porous and smooth beds
Buckley等[20]的物理模型实验证明,粗糙底床对增水的影响有两个机制,一是改变了从礁前斜坡到礁坪沿程波浪能量的空间分布,二是同时产生了底部应力。对于前者,孔隙介质带来的类似底摩擦阻力对波浪速度产生阻滞效果,使得波高和波浪能量出现衰减,相应的导致增水幅值的下降;后者源于孔隙介质(粗糙底床)对波-流场阻力的时间平均,并可用包含速度的二次方项和相应拖曳力系数的阻力定律进行估计[2-3],这一机制会导致平均水位的上升。因此这两个机制的影响互相抵消,最终导致礁坪上方的平均水位并未因为孔隙介质的存在而出现显著变化。

图8 孔隙底床和光滑底床在礁坪上方波浪增水比较Fig. 8 Comparisons of wave setup on the reef flat for the porous and smooth beds
为更清楚地展现孔隙介质的影响,将孔隙底床各工况均方波高和平均水位相对于光滑底床变化的百分比汇总在表2中。

表2 孔隙底床上均方波高和平均水位相对于光滑底床的变化百分比Table 2 Relative percentage changes of mean square wave heights and average water levels between the porous beds and the smooth beds
一些数值模型通过拖曳力系数(或底摩阻系数)与速度平方的乘积项来计算包含底部粗糙度的流动问题,认为底部粗糙度会造成平均水位上升25%~30%[27-28],与本文计算结果和相关物理实验结果之间存在较大差异。对此,有学者指出类似的方法并不能很好地处理此类冠层流动中摩擦阻力对速度的衰减,而相应的一些采用空间平均或沿水深平均的动量方程模型则能获得很好的效果[24,29]。实际上,VARANS模型也可看作一种冠层流动模型,通过本文的应用,发现其确实对于存在底部摩擦阻力的情况能准确地反映平均水位的变化,相应的,也能反映出孔隙介质的存在确实导致礁坪上方的流速产生了明显的衰减。如图9所示,对于光滑底床,礁坪上方靠近水面表现为向岸方向的流动(流速为正),而靠近水底则表现为离岸方向的流动(流速为负),礁坪上方中间的水体则处于两股反向水流的交界处,流速约为0,Yao等[30]也报导过类似的礁坪上方波生流反向分层现象。孔隙底床的礁坪上方流速出现了明显的下降,而反向的离岸流动则出现在中间层,另外,靠近水底处,由于位于孔隙介质内部,流速很小,且垂向分布较为均匀。

图9 组合4光滑底床(a)和孔隙底床(b)礁坪上方水平方向平均流速分布Fig. 9 Distribution of horizontal mean current velocities at the reef flat of Case 4 for the smooth (a) and porous (b) beds
值得指出的是,在目前关于孔隙介质的物理模型实验中[11,31-32],孔隙材料的中值粒径范围一般为1.5~2.5 cm,孔隙率则集中在0.45~0.52,本文认为,对于实验中常用的理想均一化的孔隙材料,其孔隙率下限约等于圆球体积与外切立方体的体积比,即大约为0.47。为了进一步研究孔隙介质对礁坪上方增水的影响,下面在组合4原始孔隙率为0.87的基础上,增加了0.67和0.47两种孔隙率的计算结果进行对比,如图10所示。
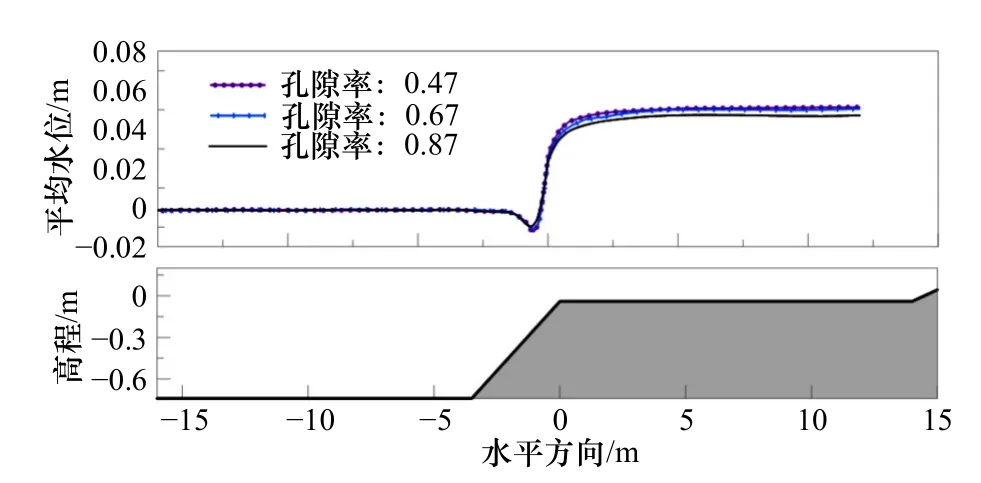
图10 组合4不同孔隙率下平均水位对比及地形剖面示意图Fig. 10 Comparisons of mean water level for Case 4 with varied porosities and the sketch of terrain profile
通过对比可以看出,孔隙率从0.87减小到0.67时,礁坪上方的增水有所上升,但变化不明显,但当孔隙率进一步减小到0.47时,礁坪上的增水变化更为微小,可以认为达到了一种类似“收敛”的效果。孔隙率变小对应的是孔隙介质的体积比增大,对应在模型实验中相当于用以模拟孔隙介质或底摩擦阻力的材料的空间布置密度增大,从直观上来说粗糙程度应当是增大的,但从计算结果看,礁坪上方的增水幅值并无明显上升,因此可以认为上文提到的底摩擦阻力对波浪增水影响不明显的论述在此得到进一步的验证。
5 结论
本文采用基于VARANS方程的非静压波浪模型对随机波浪典型斜坡-礁坪地形上的传播进行了模拟,重点分析了孔隙介质对礁坪上方均方波高和平均水位变化的影响。通过和相应物理模型实验结果的对比,证明了本文模型能有效处理波浪和孔隙介质的相互作用,与实验测量结果保持了很高的一致性。通过分析,发现孔隙介质对波高的衰减作用较为明显,相比于光滑底床条件,在波浪破碎点附近,孔隙底床的波高下降了12%,礁坪上方波高平均下降28%。对于平均水位,孔隙底床条件下的最大减水幅值减小了43%,同时礁坪上方增水上升6%。相比于波高的变化,礁坪上方增水的变化比较小,但与实验测量的结果相一致,可以认为孔隙介质(类似于底摩擦阻力的作用)的存在对礁坪上方的增水影响不明显。另外,孔隙率(0.47~0.87)在一定范围内变化时,对平均水位的影响不明显,也从另一个方面证明了孔隙介质对礁坪上方的增水影响很小。
