HY-2C卫星海面高度数据的质量分析
2022-09-25孟菊于方杰庄志远齐娟娟陈戈
孟菊,于方杰,,庄志远,齐娟娟,陈戈,
( 1. 中国海洋大学 信息科学与工程学部 海洋技术学院,山东 青岛 266100;2. 青岛海洋科学与技术试点国家实验室 区域海洋学与数值模拟实验室,山东 青岛 266237)
1 引言
海洋二号C(HY-2C)卫星是我国第三颗海洋动力环境卫星,该卫星集主、被动微波遥感于一体,属于我国海洋系列遥感卫星,具有高精度测轨、定轨能力与全天候、全天时、全球探测能力。卫星的主要使命是监测和调查海洋环境,获得海面高度等多种海洋动力环境参数,直接为灾害性海况预警预报提供实测数据,为海洋防灾减灾、海洋权益维护、海洋资源开发、海洋环境保护、海洋科学研究以及国防建设等提供支撑服务。
相对定标是国内外学者主要采用的一种数据质量和精度评估方式,其优点是可以实现在全球范围内对数据进行分析,而不存在观测设备高精度要求和地域限制。通过对星间数据的交叉点分析可探测卫星系统异常和地域性误差特征,评估卫星的测量精度,为实现卫星系统改进和有效应用卫星数据提供定量依据[1-5]。相对定标分为单颗卫星升降轨道的自交叉和不同卫星升降轨道之间的互交叉。卫星自交叉点分析是高度计数据质量评估的重要指示,此方法可用来评价高度计数据的稳定性。互交叉点分析广泛应用于利用校准后的卫星雷达高度计数据对新发射的卫星雷达高度计数据进行评估[6-7]。已有Jason-2、Jason-3、HY-2A、HY-2B等卫星通过相对交叉定标对海面高度进行了评估[1,3,6,8-10]。用交叉定标获取交叉点的插值方法不尽相同,Jiang等[6]利用邻近观测点插值的方法获取交叉点,在时间窗口为3 d、纬度小于60°、水深大于200 m、交叉点的高度异常差小于10 cm的条件下对HY-2A卫星进行评估,结果显示HY-2A和Jason-2卫星的交叉点海平面高度异常差值的平均值为4.19 cm,标准差达到4.98 cm,HY-2A卫星成功达到国际同类高度计的测高水平;刘亚龙[1]利用了三次样条插值的方法获取交叉点,在时间窗口为3 d、纬度小于50°、水深大于1 000 m、海面变化小于20 cm的条件下对HY-2A卫星进行评估,结果显示HY-2A和Jason-2卫星测量的海平面高度差值平均值为0.26 cm,均方根误差为6.61 cm,交叉定标精度达到国际同类高度计精度水平,表明 HY-2A卫星高度计观测海面高度稳定可靠;刘治中等[9]在Jason-2与Jason-3卫星高度计编队飞行阶段利用最邻近方法获取交叉点,结果显示Jason-3和Jason-2卫星高度计的交叉点海平面高度差值的标准偏差仅在0.06 cm左右。以上为3种比较典型的获取交叉点的方法。而国内对于HY-2C卫星的数据质量分析的文章非常少,目前有Wang等[11]通过利用浮标、欧洲中期天气预报中心模型和其他散射计风速参数与HY-2C卫星的风速参数进行对比,对HY-2C卫星风速参数的准确性进行了评估。最近Kong等[12]提出了一种直接利用星载多普勒轨道和卫星无线电定位(DORIS)数据来验证HY-2C卫星轨道精度的新方法。Wang等[13]提出了一种通过深度学习采集宽幅有效波高的方法。截至目前,还未见到有关HY-2C卫星高度计数据质量的报告。所以实现对HY-2C卫星海面高度精度分析至关重要,有利于实现后续对于HY-2C卫星在海洋观测上的应用。
本文主要对HY-2C卫星高度计遥感地球物理数据(Sensor Geophysical Data Records, SGDR)中的海面高度数据进行全球质量分析。本文以Jason-3卫星和HY-2B卫星同期观测的地球物理数据(Geophysical Data Records, GDR)为参考,对HY-2C卫星的SGDR进行数据完整性和有效性分析,分析HY-2C卫星数据质量;并且使用3种常见的交叉定标插值方法对HY-2B、Jason-3、HY-2C卫星雷达高度计SGDR的海面高度异常数据进行自交叉点分析,探究不同的插值方法对卫星高度计海面高度数据质量分析结果的影响;最后通过分别与HY-2B卫星、Jason-3卫星GDR的海面高度异常数据进行互交叉点计算,完成对HY-2C卫星海面高度数据的质量分析。
2 数据
2.1 数据源
HY-2C卫星高度计SGDR发布于国家卫星海洋应用中心,从2020年9月24日开始发布。用户可以从中国海洋卫星数据服务系统(https://osdds.nsoas.org.cn/)下载,本文使用了HY-2C卫星雷达高度计第13~21周期的SGDR,时间范围是2021年1月21日至4月20日。SGDR是利用MOE(Medium Accuracy Orbit Ephemeris)定轨数据和波形重构等方法得到的未经校正的数据产品,数据中除了主要包括有效波高、海面风速、海面高度及用于计算海面高度所需的相关校正参数,还包含波形数据。因为HY-2B、Jason-3卫星高度计已经在现场经过校准,具有较高的数据质量,所以本文利用HY-2B、Jason-3卫星高度计采集的同期GDR作为对比数据,对HY-2C卫星高度计的海面高度数据进行质量分析。
目前HY-2C卫星只发布了MOE精密定轨的SGDR。从SGDR到GDR的制作流程缺少一个精密定轨校正,因此,利用HY-2B、Jason-3卫星对HY-2C卫星的海面高度数据定标结果可能会因为数据产品的不同存在系统偏差。
2.2 数据处理
HY-2C卫星和HY-2B、Jason-3卫星的海平面高度(Sea Surface Height, SSH)和海平面高度异常(Sea Level Anomaly, SLA)采用下面的公式计算:
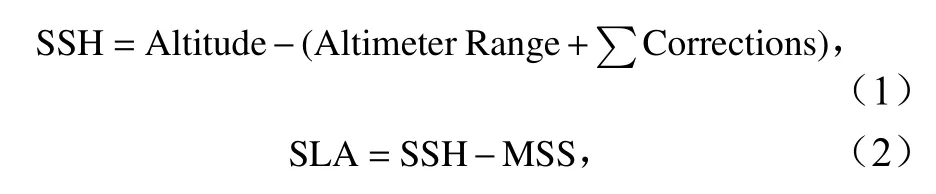
式中,Altitude表示轨道的高度;Altimeter Range表示高度计测距值;Corrections表示干对流层延迟、湿对流层延迟、模型电离层延迟、逆大气压改正、海潮、极潮、固体潮和海况偏差改正项之和;MSS为在一个较长的时期之内剔除了年际、半年际、季节性和其他周期性的海面高度变化信息之后平均的海面高度。本文中HY-2C卫星的SGDR、HY-2B卫星的GDR、Jason-3卫星的GDR中使用的MSS均来自MSS CLS2015模型(https://www.aviso.altimetry.fr/en/data/products/auxiliary-products/mss.html)。该模型是由法国卫星中心利用1993-2012年卫星测高数据中的海平面高度数据解算得到的。SLA可以很好地捕捉海洋变化特征,利用SLA来检验卫星高度计的高度测量能力要比用海平面高度来检验更为准确[4-6,9]。所以本文用SLA来检验卫星高度计的精度。
2.3 数据完整性与有效性分析
通过数据编辑标准可以剔除掉高度计测量中精度较低的值,得到有效的观测结果[7,10,14]。对不同的参数,编辑标准按照最大阈值和最小阈值的方式定义,阈值范围外的参数都需要被剔除。为了提高数据的时空相关性,对HY-2C卫星采用和HY-2B、Jason-3卫星一致的数据编辑策略,本文采用的是Jason-3卫星用户手册中二级产品(O)(I)GDR 的编辑标准。主要编辑标准见表1。
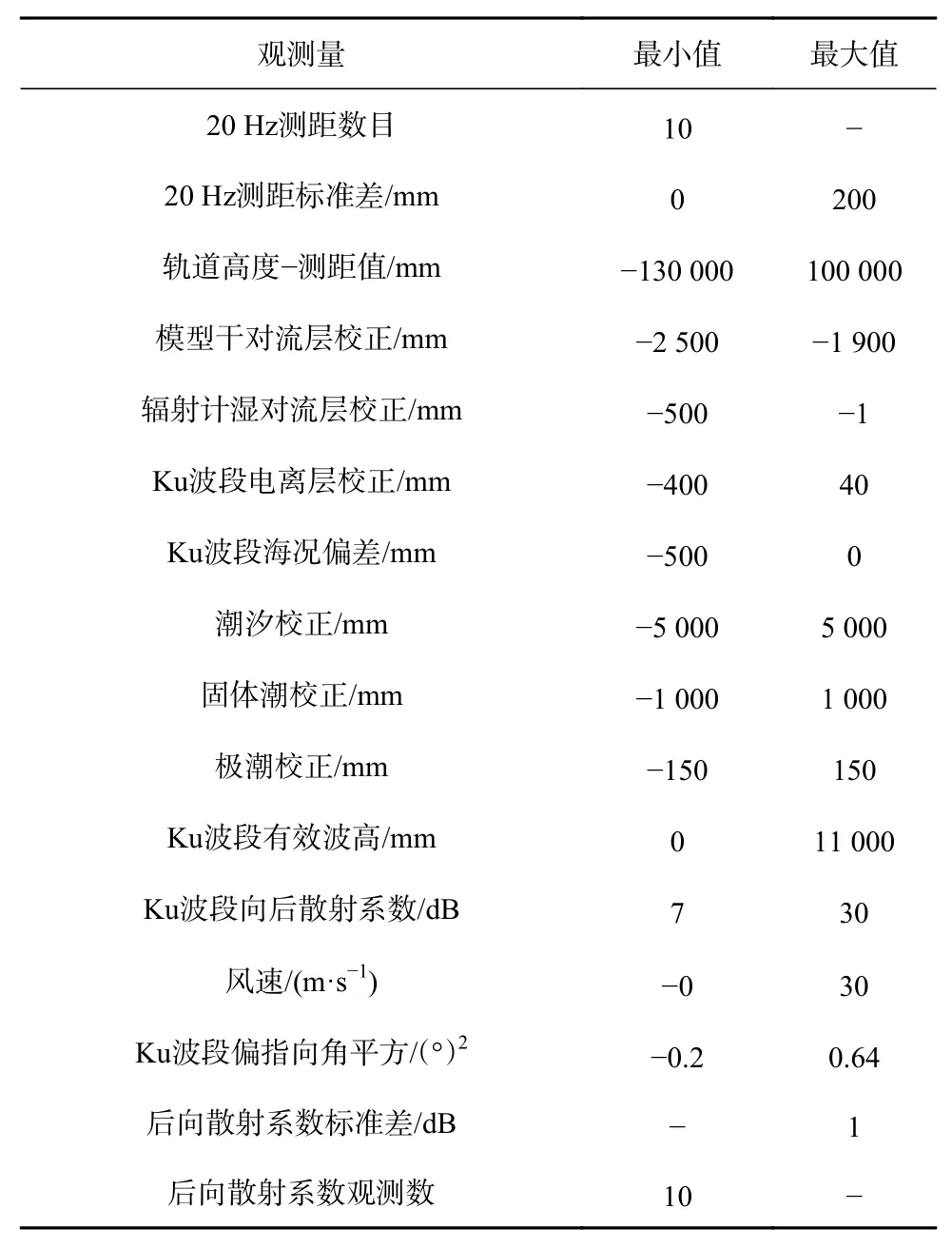
表1 HY-2C卫星、HY-2B卫星和Jason-3卫星高度计和辐射计数据编辑的参数阈值Table 1 Main editing thresholds values of HY-2C satellite, HY-2B satellite and Jason-3 satellite altimeters and microwave radiometers
为了准确分析HY-2C卫星高度计在海洋中的测量精度,我们除了通过表1对数据筛选,还进行了以下条件的限制:
(1)为了排除海冰的影响,将纬度限制在南北纬50°之间[14]。
(2)为了排除近海的影响,将水的深度限制在大于1 000 m的海域[14]。
(3)为了减少时间变化对海面高度的影响,交叉点处的最大时间间隔为3 d[14]。
(4)为了剔除一些异常值,卫星交叉点处的SLA之差应该大于20 cm[6-7,14]。
2.3.1 数据完整性分析
通过分析卫星轨迹数量来检验卫星高度计的完整性。理论上HY-2C卫星1个完整周期有274个轨迹,但实际上由于卫星测量模式的调整或其他原因(地面接收站问题或数据传输异常,也可能是由于地面控制等[7,15]),导致HY-2C卫星SGDR存在轨迹缺失现象。图1a为HY-2C卫星每周期的轨道数据缺失情况,其中第21周期轨道数据缺失可能是因为数据传输异常,导致出现数据冗余。HY-2B卫星1个完整周期有386条轨迹,图1b是HY-2B卫星每周期轨道数据缺失情况,在和HY-2C卫星相同的时间段内,HY-2B卫星和HY-2C卫星一样存在着数据缺失和冗余现象。图1c是Jason-3卫星每周期的轨道数据缺失情况,Jason-3卫星的GDR 1个完整周期有254个轨迹,在和HY-2C卫星相同的时间段内,Jaosn-3卫星的数据相对稳定,卫星轨道数据未产生缺失和冗余现象。

图1 HY-2C卫星(a)、HY-2B卫星(b)和Jaosn-3卫星(c)不同周期数据缺失轨迹个数Fig. 1 Data missing pass number of HY-2C satellite (a), HY-2B satellite (b) and Jason-3 satellite (c)
2.3.2 数据有效性分析
计算SLA时,按照表1的编辑标准对测高数据进行编辑,可以将不符合条件的观测数据滤除。数据的编辑比例指的是不符合约束条件被滤除的数据比例,能够反映出卫星测高数据的质量,编辑比例越低,有效性越好[8,16]。
根据表1给定的阈值对卫星数据产品进行约束,从而得到HY-2C卫星和Jason-3卫星的数据编辑比例,如图2a所示,在没有经过海深和纬度约束的情况下,HY-2C卫星数据编辑比例的均值为30.7%,标准差为6.62%;HY-2B卫星数据编辑比例的均值为39.9%,标准差为5.29%;Jason-3卫星数据编辑比例的均值为34.17%,标准差为0.60%。在海深1 000 m以下和纬度在南北纬50°之间的条件下,得到HY-2C卫星、HY-2B卫星、Jason-3卫星数据编辑比例(图2b),HY-2C卫星数据编辑比例的均值为14.02%,标准差为8.18%;HY-2B卫星数据编辑比例的均值为12.20%,标准差为7.64%;Jason-3卫星数据编辑比例的均值为2.44%,标准差为0.39%。从全球范围来看,HY-2C卫星的有效数据点更多。在海深1 000 m以下和纬度在南北纬50°之间的限制条件下,Jason-3卫星数据有效点更多。并且HY-2C卫星、HY-2B卫星和Jason-3卫星不符合编辑标准的数据产品多集中在高纬度和浅海地区。

图2 HY-2C卫星、HY-2B卫星和Jason-3卫星在无海深和纬度约束的数据编辑比例(a)和有海深和纬度约束的数据编辑比例(b)Fig. 2 The editing ratio of HY-2C satellite, HY-2B satellite and Jason-3 satellite measurements without sea depth and latitude constraints (a) and with depth and latitude constraints (b)
3 研究方法
3.1 确定交叉点精确的位置
卫星测高技术发展早期通常只对独立的一颗卫星进行处理,因此交叉点被认为只是升弧段和降弧段的交点[17-18]。随着时代的发展,卫星高度计的数量越来越多,多种卫星数据的联合处理成为趋向。对于卫星倾角不同的情况,还要考虑到升弧段与升弧段、降弧段与降弧段也可能存在交叉点。因此本文在此基础上做了改进,不再对轨道的升降进行判断,而是直接判断卫星轨道地面轨迹是否有交叉点。首先直接输入两个卫星轨道,根据轨道的两个端点坐标拟合二元一次线性方程组,公式为

式中,A是拟合得到的卫星轨道的系数;B是拟合得到的卫星轨道的截距;x是经度坐标;y是纬度坐标。本文中设定卫星数据的经度范围为0°~360°,其中0°~180°代表东经,180°~360°代表西经;纬度范围为-90°~90°,正值代表北纬,负值代表南纬。通过拟合得到两个卫星轨道的二元一次方程,联立方程组判断是否有解。如果没有解,进一步判断是否是由卫星跳变引起(如果卫星轨迹穿过本初子午线,其星下点经度在0°(360°)附近会产生跳变),判断卫星轨道地面轨迹两个端点经度差的绝对值是否大于180°,如果大于180°,通过减去360°的方法使经度变化连续。然后再一次联立方程组进行判断是否有解,有解的情况下我们认为两个轨道相交。在这个条件下,遍历求出两颗卫星轨道星下点之间距离在1°范围内的星下点。由于两颗卫星轨道星下点之间距离在1°的范围内的星下点数较少,轨道也较短,因此可以视作直线。根据公式(3)输入两个端点坐标,求出两个轨道地面轨迹的二元一次方程,联立方程组得到近似交叉点位置(在1°范围内拟合的直线求出来的交叉点肯定和实际交叉点存在一定距离)。在近似交叉点位置的0.4°、0.6°、0.8°范围内分别再对轨道点拟合直线方程组求交叉点,选取在近似交叉点范围内最近的距离拟合出来的交叉点作为精确交叉点。通过卫星数据产品计算得到的HY-2C卫星两条轨道之间的距离在1°范围内的星下点以及精确交叉点位置如图3所示。
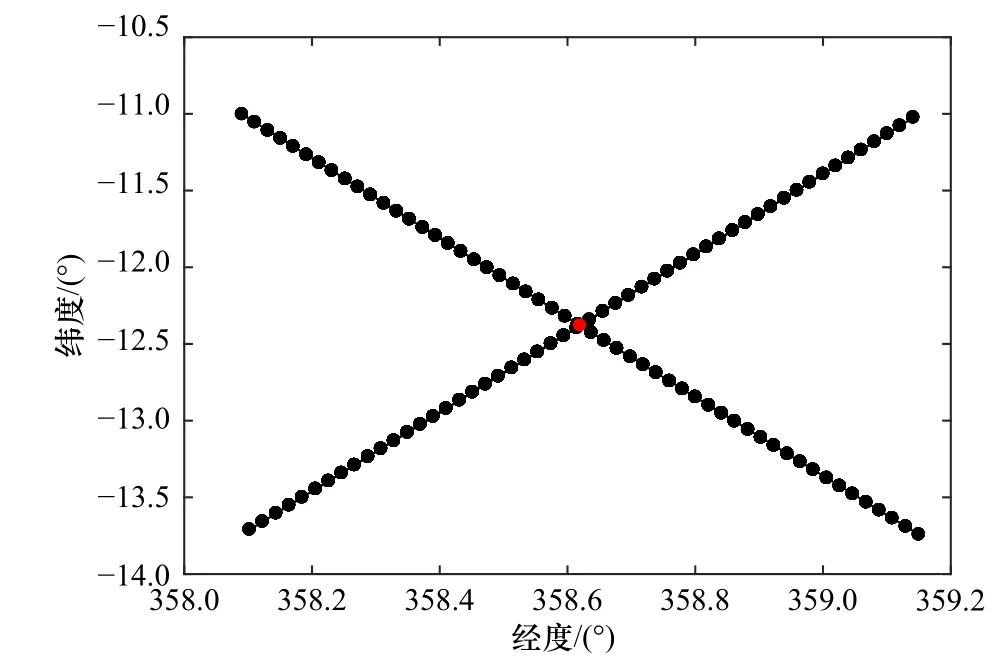
图3 HY-2C卫星两条轨道星下点之间距离在1°范围内示意图Fig. 3 Schematic diagram of the distance between the subsatellite points of the two orbits of the HY-2C satellite within 1°
3.2 确定交叉点海面高度异常
在求取交叉点精确位置之后,为了比较在星星交叉定标中使用不同的插值方法是否会影响到卫星高度计的海面高度数据质量结果,本文用3种典型的交叉定标插值方法将SLA插值到交叉点精确位置。
方法一(临近点插值):在两颗卫星轨道星下点之间距离在1°范围内的所有星下点中选择距离交叉点最近的两个星下点。如图4所示,每条轨道选择距离交叉点最近的两个星下点,然后通过式(4)计算交叉点海面高度异常。
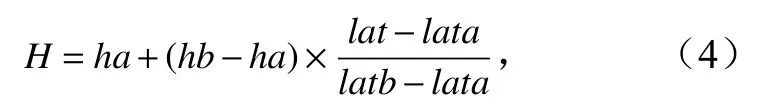
式中,H是不同轨道交叉点插值得到的SLA;ha是纬度较小星下点的SLA;hb是纬度较大星下点的SLA;lat是交叉点的纬度值;lata是纬度较小星下点的纬度值;latb是纬度较大星下点的纬度值。

图4 临近点插值示意图Fig. 4 Schematic of the near observation point interpolation
方法二(最近点插值):在两颗卫星轨道星下点之间距离在1°范围内的所有星下点中选择距离交叉点最近的一个星下点,如图5所示,将最近星下点的高度异常作为精确交叉点位置的海面高度异常。

图5 最近点插值示意图Fig. 5 Schematic of the nearest observation point interpolation
方法三(三次样条插值):为了通过三次样条函数得到更好的插值效果,要保证距离1°范围内的两颗卫星轨道交叉点两侧至少存在4个点以上,如图中蓝色的卫星星下点(图6 )。然后通过三次样条插值把选取的星下点的海面高度异常插值到精确交叉点位置。

图6 三次样条插值示意图Fig. 6 Schematic of the cubic spline interpolation
卫星轨道的自交叉是评估和确认测高精度稳定性的重要手段。为了了解在星星交叉定标中使用不同的插值方法是否会影响卫星高度计的海面高度数据质量结果,本文在交叉定标中使用了3种典型插值方法对HY-2C卫星、HY-2B卫星、Jason-3卫星的数据质量进行自交叉点分析。为了减少时间变化对海面高度的影响,卫星交叉点处的最大时间间隔限制为3 d。采用交叉点海面高度异常差的平均值和标准差来对海面高度数据质量进行评估。理想情况下,交叉点海面高度异常差的平均值将接近0,标准差将非常小[3,5]。这种评估方法已经被用于TOPEX/Poseidon、Jason-1、Jason-2、Jason-3、Sentinel-3A、SARAL和HY-2A等卫星高度计高度产品的精度评估[6-10,12,15]。表2至表4是HY-2C卫星、HY-2B卫星和Jason-3卫星进行自交叉点分析的结果。
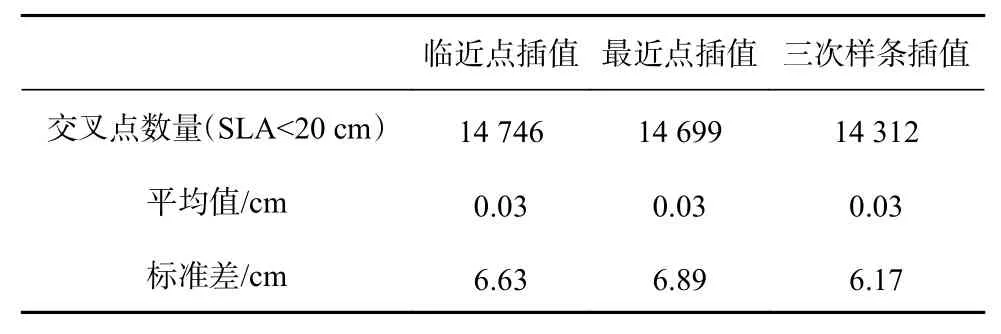
表2 HY-2C卫星自交叉点海面高度异常数据精度的比较Table 2 Comparison of accuracy in HY-2C satellite self-crossover sea level anomaly data

表3 HY-2B卫星自交叉点海面高度异常数据精度的比较Table 3 Comparison of accuracy in HY-2B satellite self-crossover sea level anomaly data
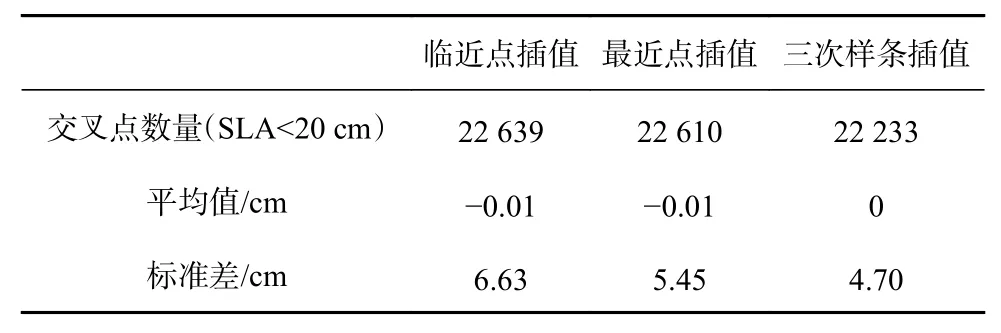
表4 Jason-3卫星自交叉点海面高度异常数据精度的比较Table 4 Comparison of accuracy in Jason-3 satellite self-crossover sea level anomaly data
上述3种交叉定标得到的交叉点数量相近,HY-2C卫星、HY-2B卫星和Jason-3卫星使用三次样条插值可以得到最优的结果。结果表明,HY-2C卫星、HY-2B卫星和Jason-3卫星在星星交叉定标中使用不同的插值方法会影响卫星海面高度数据质量评估的结果,并且本文经过对3种插值方法的比较后得出三次样条插值法相较于前两种方法更适合对卫星数据质量进行分析。为了避免不同的插值方法对HY-2C卫星SGDR产品的海面高度数据质量分析结果造成影响,在后续对卫星的海面高度数据质量进行分析时,将使用三次样条插值获取交叉点。
4 结果与分析
4.1 HY-2C自交叉点分析
通过分析交叉点海面高度差值可以实现对高度计海面高度质量的评估,表2结果显示,对HY-2C卫星高度计SGDR中海面高度异常数据进行自交叉点分析的平均值为0.03 cm,标准差为6.17 cm。这证明了HY-2C卫星高度计观测性能的稳定性。
为了更好地对HY-2C卫星海面高度数据质量进行评估,选取从2021年1月21日至4月20日相同时间段内的HY-2B卫星数据和Jason-3卫星数据进行周期内海平面高度异常差异平均值和标准差的比较,如图7所示。

图7 HY-2C卫星(a)、HY-2B卫星(b)和Jason-3卫星(c)自交叉点海平面高度异常差的平均值(蓝色)和标准差(红色)Fig. 7 Mean error (blue dotted lines) and standard deviation(red dotted lines) of HY-2C satellite (a), HY-2B satellite (b) and Jason-3 satellite (c) self-crossover sea level anomaly data
如图7a所示,HY-2C卫星各个观测周期自交叉点海面高度异常差的平均值在0 cm上下波动,标准差在6 cm上下波动。图7b和图7c是在和HY-2C卫星相同的数据筛选标准和限制条件下得出的结果。图7b显示,HY-2B卫星各个观测周期自交叉点海面高度异常差的平均值在0 cm上下波动,标准差在4 cm上下波动。图7c显示,Jason-3卫星各个观测周期的交叉点海面高度异常差的平均值在0 cm上下波动,标准差在5 cm上下波动。HY-2C卫星与HY-2B卫星、Jason-3卫星的自交叉定标结果相近,卫星间海面高度异常差异自交叉结果的均值在0.02 cm以内,标准差在2 cm以内,这些结果证实HY-2C卫星高度计测高能力与HY-2B卫星、Jason-3卫星的相近。
4.2 HY-2C卫星与HY-2B卫星和Jason-3卫星互交叉点比较分析
对HY-2C卫星和HY-2B卫星、Jason-3卫星的海面高度异常数据进行互交叉点分析的方法和自交叉点分析的计算方法一样。HY-2C卫星和HY-2B卫星、Jason-3卫星互交叉点海面高度异常数据统计结果如表5所示,HY-2C卫星和HY-2B卫星海面高度异常差异的平均值为-0.47 cm,标准差为5.32 cm。HY-2C卫星和Jason-3卫星海面高度异常差异的平均值为-0.3 cm,标准差为5.32 cm。图8a显示了HY-2C卫星和HY-2B卫星在不同观测周期内互交叉点海面高度异常差异的平均值和标准差的变化,平均值在-1~0 cm之间波动,标准差在5 cm上下波动。图8b显示了HY-2C卫星和Jason-3卫星在不同观测周期内互交叉点海面高度异常差异的平均值和标准差的变化,平均值在-1~1 cm之间波动,标准差在5 cm上下波动。结果非常接近Jia等[7]提供的HY-2B卫星和Jaosn-3卫星互交叉点精度水平。

表5 HY-2C卫星和HY-2B卫星、Jason-3卫星互交叉点海面高度异常数据精度的比较Table 5 Comparison of accuracy in HY-2C satellite and HY-2B satellite, HY-2C satellite and Jason-3 satellite cross-crossover sea level anomaly data
5 结论
本文使用了HY-2B卫星、Jason-3卫星同期观测数据对我国HY-2C卫星雷达高度计SGDR产品第13~21周期的海面高度数据进行质量分析。HY-2C卫星在全球范围内的有效数据点较多,不符合观测条件的数据产品多集中在高纬度和浅海地区。使用临近点插值、最近点插值、三次样条插值法分别对3颗卫星的海面高度异常数据进行了自交叉点分析,从均值和标准差来看,在星星交叉定标中使用三次样条插值法对HY-2C卫星、HY-2B卫星、Jason-3卫星的定标结果最好。这说明在星星交叉定标中使用合适的插值方法会影响卫星高度计的海面高度数据质量分析结果,此外,HY-2C卫星和HY-2B卫星互交叉点海面高度异常差异的平均值为-0.47 cm,标准差为5.32 cm;HY-2C卫星和Jason-3卫星互交叉点海面高度异常差异的平均值为-0.3 cm,标准差为5.32 cm。这些数据表明HY-2C卫星的测高精度接近Jason-3卫星的数据,说明HY-2C卫星的测高精度与HY-2B卫星和Jason-3卫星一致,均具有较高的精度。本文研究结果还可为HY-2C卫星SGDR的应用提供依据,并为GDR的生产提供参考。

图8 HY-2C卫星和HY-2B卫星(a)、HY-2C卫星和Jason-3卫星(b)互交叉点海平面高度异常差异的平均值(蓝色)和标准差(红色)Fig. 8 Mean error (blue dotted lines) and standard deviation(red dotted lines) of HY-2C satellite and HY-2B satellite (a),HY-2C satellite and Jason-3 satellite (b) cross-crossover sea level anomaly differences
