求解置换流水车间调度问题的混合鸟群算法

闫红超，汤伟*，姚斌

（1.陕西科技大学电气与控制工程学院，西安 710021；2.陕西科技大学电子信息与人工智能学院，西安 710021）

0 引言

生产调度是实现先进制造的基础和关键，高质量的调度方案能够降低生产成本、提高资源利用率和生产效率，从而增强企业的竞争力。置换流水车间调度问题（Permutation Flowshop Scheduling Problem，PFSP）主要研究n个工件在m台机器上的加工过程，目的是找到一个工件排序使得调度目标最优。基于PFSP 的生产模式在制造业中存在广泛的应用场景；然而，3 台机器以上的PFSP 属于NP-hard 问题［1］，求解困难，因此，研究和开发高效的求解算法具有重要的理论价值和现实意义。

解决PFSP 的有效方法包括最优求解法和近似求解法。最优求解法是基于模型的方法，主要有分支定界、整数规划、动态规划以及拉格朗日松弛法等。由于计算复杂度高，最优求解法通常仅适用于求解小规模的PFSP［2］。近似求解法主要包括启发式算法和元启发式算法。启发式算法主要有NEH（Nawaz-Enscore-Ham）算法［3］、Johnson 规则［4］等，这些算法虽然能在短时间内构造出解，但难以保证质量。近年来元启发式算法在车间调度中得到了广泛的应用，主要有基于变邻域搜索的粒子群优化（Particle Swarm Optimization based on Variable Neighborhood Search，PSOVNS）算法［5］、分布估计算法（Estimation of Distribution Algorithm，EDA）［6］、Liu 等［7］提出的混合差分进化（Hybrid Differential Evolution algorithm proposed by Liu et al，L-HDE）算法、双种群协同学习（Double Population Co-Learning，DPCL）算法［8］、混合共生生物搜索（Hybrid Symbiotic Organisms Search，HSOS）算法［9］等。

鸟群算法（Bird Swarm Algorithm，BSA）是由Meng 等［10］提出的一种基于鸟群行为的群智能优化算法，主要思想来源于对鸟群觅食、警戒和飞行等群体行为的模拟以及对鸟群觅食过程中共享信息的研究。相比差分进化算法、粒子群优化算法等常见的传统优化算法，该算法独有的多路径搜索机制使其更好地平衡了高效性与准确性［11］。BSA 已经在动态能耗管理［11］、微电网优化配置［12］、离散智能车间调度［13］和柔性作业车间调度［14］等方面得到了应用。

目前还查阅不到基于鸟群算法对置换流水车间调度问题（PFSP）的研究。本文针对以最大完工时间最小化为目标的PFSP，提出了一种混合鸟群算法（Hybrid Bird Swarm Algorithm，HBSA）进行求解。首先，结合一种基于NEH 的启发式算法和混沌映射提出了一种新的种群初始化方法，以改善初始种群的质量和多样性；其次，采用最大排序值（Largest Ranked Value，LRV）规则［7］将连续的位置值转换为离散的工件排序，从而使算法能够处理离散的调度问题；最后，借鉴变邻域搜索（Variable Neighborhood Search，VNS）和迭代贪婪（Iterated Greedy，IG）算法的思想针对个体最佳工件排序和种群最佳工件排序分别提出了局部搜索方法，以强化算法对解空间的探索能力。针对广泛使用的Rec标准测试集［15］进行仿真测试，并将结果与多种算法的结果进行比较，以验证算法的性能。

1 置换流水车间调度问题

置换流水车间调度问题的描述为：已知各个工件在各台机器上的加工时间，要求找到各工件在机器上的加工顺序使得某个调度目标最优。相关的约束条件有：一台机器在同一时刻只能加工一个工件；一个工件在同一时刻只能被一台机器加工；每台机器上的工件加工顺序相同；工件一旦在机器上开始加工就不能中断；不考虑所有工件的准备时间；开始时间为零。

生产调度的最终目的是在满足约束条件的前提下，合理安排现有资源、提高生产效率，使成本最小化或效益最大化，因此最小化最大完工时间是主要的调度目标。

假 设J={J1，J2，…，Jn} 为n个工件的集合；M={M1，M2，…，Mm} 为m台机器的集合 ；π=[π(1)，π(2)，…，π(n)]为所有工件的一个排序，表示加工顺序为从π(1)到π(n)；P(i，j)为工件π(i)在机器Mj上的加工时长；C(i，j)为工件π(i)在机器Mj上的完工时间。各个工件在各台机器上的完工时间可按照如下方法进行计算：

工件排序π对应的最大完工时间Cmax为最后一个工件在最后一台机器上的完工时间，即

求解以最大完工时间最小化为调度目标的PFSP，目的是找到一个工件排序π*，使得：

式中Π为所有工件排序的集合。

PFSP 是一种典型的组合优化问题，且有研究表明3 台机器以上的PFSP 属于NP-hard 问题，具有指数爆炸、工序相关等复杂性，求解非常困难。针对该问题，本文提出一种混合鸟群算法（HBSA），用于更加有效地最小化最大完工时间。

2 混合鸟群算法

2.1 基本鸟群算法（BSA）

如果rand(0，1) ＜P，则鸟儿进行觅食；否则进行警戒。rand(0，1)为(0，1)区间均匀分布的随机数，P为(0，1)区间的一个固定值。

觅食行为的位置更新策略为：

式中：C为认知加速系数；S为社会加速系数；pi表示第i只鸟的历史最优位置；g代表整个种群的历史最优位置；t=1 时，每只鸟的历史最优位置为其初始位置，种群的历史最优位置为初始种群的最优位置。

警戒行为的位置更新策略为：

假设每隔FQ间隔，鸟群会飞到另一个地方，FQ是一个正整数。

生产者的位置更新策略为：

式中：randn(0，1)表示均值为0、标准差为1 服从高斯分布的随机数。

乞食者的位置更新策略为：

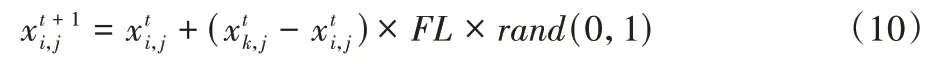
式中：FL∈[0，2]表示乞食者跟随生产者去寻找食物。

2.2 求解PFSP的混合鸟群算法

基本鸟群算法仅适用于求解连续性问题，对于离散的PFSP 不能直接使用；与其他群智能优化算法相似，基本鸟群算法在处理复杂问题时，存在易陷入局部最优、易过早收敛、收敛精度差等缺点。

为了弥补上述不足，采用LRV 规则将连续的位置值转换为离散的工件排序，使得算法可用于求解PFSP；结合一种基于NEH 的启发式算法和混沌映射来初始化种群，以改善初始种群的质量和多样性、提升算法迭代的效率；借鉴变邻域搜索和迭代贪婪算法的思想对个体最佳工件排序和种群最佳工件排序进行局部搜索，以强化算法对解空间的探索能力，从而提出了一种混合鸟群算法（HBSA）。HBSA 的流程如图1 所示，其中，种群（个体）最佳工件排序是指种群（个体）历史最优解对应的工件排序。

图1 HBSA流程Fig.1 Flow chart of HBSA

2.2.1 编码方式与LRV转换

采用LRV 规则将表示位置的一组连续值映射成工件排序，使鸟群算法能用于解决离散的PFSP。具体方法是每次从代表位置的一组连续值中选择最大值所属的维度作为下个要加工的工件，直至遍历所有的位置值。空间维度D取值为工件的数量n。如图2 所示，根据LRV 将一个6 维空间中个 体i的位置xi=[1.25，-0.79，4.01，-0.52，-1.30，1.15］，转换为一个工件排序πi=[2，5，1，4，6，3]。

图2 LRV规则表示方法Fig.2 Representation of LRV rule

将工件排序πi对应的最大完工时间Cmax(πi)作为第i只鸟的适应度值f(i)，即

显然，最大完工时间最小的个体为种群最优个体，种群最优个体对应的最大完工时间为种群最优解。

2.2.2 种群初始化

好的初始种群有助于提升算法迭代的效率、提高算法的性能。启发式算法能够在较短时间内获得质量较高的解，保证初始种群中有质量较高的个体；混沌是非线性系统普遍存在的现象，具有有界性、随机性、遍历性等特点［16］，采用混沌映射初始化种群，可使个体离散地分布在解空间内，从而有效地提高种群的多样性，因此，结合启发式算法和混沌映射进行种群初始化以提高初始种群的质量和多样性。

1）NEHLJP1 启发式算法。

NEHLJP1 是Liu 等［17］提出的一种基于NEH 的改进算法，该算法较NEH 具有更强的寻优能力，且计算复杂度和NEH相同。NEHLJP1 算法的步骤如下：

步骤1 计算工件i(i=1，2，…，n)在所有机器上加工时长的平均值AVGi、标准偏差STDi和偏度SKEi，并根据AVGi+DEVi+abs(SKEi)的结果按照非增的顺序排序，得到优先序列γ，其中abs()表示取绝对值。

步骤2 令工件排序π=[γ(1)]，j=2。

步骤3 将工件γ(j)插入到π中使最大完工时间最小的位置。如果存在多个位置，则根据Liu 等［17］提出的择优（Tie Breaking，TBLJP1）机制决定最终的插入位置。

步骤4 令j=j+1，若j≤n，则继续执行步骤3；否则，π即为最终的工件排序，算法结束。

2）Logistic 映射。

Logistic 映射是一种典型的混沌映射系统，对应的系统方程［18］为：

式中：Xk为混沌变量，μ是控制变量。通常取μ=4，此时系统处于完全混沌状态，X遍历整个［0，1］区间。

3）种群初始化。

按照下述方法产生规模为N的初始种群：首先使用NEHLJP1 产生的解初始化种群中约10%的个体，然后用Logistic 映射产生其余的个体。具体方法为：

步骤1 基于NEHLJP1 产生一个工件排序π。令InitNum=

步骤2 使用π生成InitNum个个体：

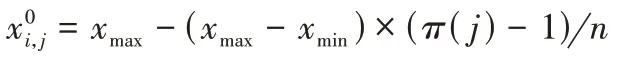
式 中 ：i∈{1，2，…，InitNum}，j∈{1，2，…，n}，xmax=5，xmin=-5。

步骤3 采用Logistic 映射生成剩余的个体：

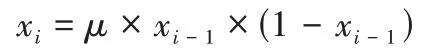
式中：i∈{}InitNum+1，InitNum+2，…，N。特别地，xInitNum为随机生成的n维混沌变量。

2.2.3 局部搜索与改进技术

变邻域搜索（VNS）和迭代贪婪（IG）算法是简单、有效的局部搜索技术。

VNS 通过多种邻域操作强化算法对解空间的探索能力［5，7］，其中，插入和交换是最常用的操作。对于工件排序π中随机的两个位置j，k∈{1，2，…，n}∧j≠k，插入是将位置j上的工件取出并插入到位置k从而得到新的工件排序π'，如图3 所示；交换则是将这两个位置上的工件互换从而得到新的工件排序π'，如图4 所示。

图3 插入操作实例Fig.3 Example of insert operation

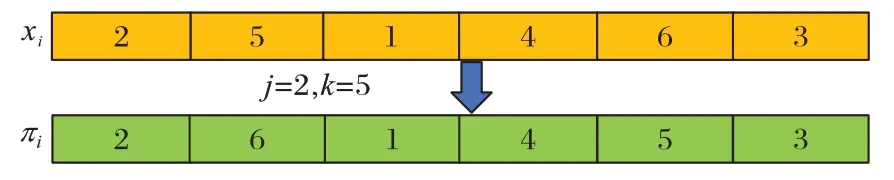
图4 交换操作实例Fig.4 Example of swap operation

IG 基于插入邻域通过不断地解构（Destruction）、构造（Construction）和局部搜索（Local Search）以提升解的 质量［19-20］。解构即从工件排序π中随机抽取d个工件（每次抽取1 个，抽取d次），其他工件的顺序保持不变，从而得到d个被删除工件的排列πR和剩余n-d个工件的排列πD；构造则是将πR中的工件按照被抽取的顺序依次插入到πD中使最大完工时间最小的位置，从而得到完整的工件排序π'；局部搜索基于插入邻域对π'进行局部搜索以提升π'的质量。

为了弥补基本鸟群算法易陷入局部最优、易过早收敛、收敛精度差等不足，借鉴VNS 和IG 算法的思想提升个体历史最优解和种群历史最优解的质量，主要思想为：

1）采用VNS 产生新解。基于插入邻域产生新解并对其进行优劣评估，以充分利用其简单、高效的优点；基于交换邻域产生扰动，以进一步强化算法跳出局部最优的能力。

2）引入TBLJP1机制。工件插入过程中易产生大量具有最小最大完工时间而顺序不同的工件排序，如何选择对算法最终的优化结果有着显著的影响，因此引入TBLJP1机制进一步择优。

3）由于工件的插入会对离插入位置近的工件产生较大的影响［21］，因此在构造过程中，将插入位置前面及后面的工件去除并重新插入。为了节约计算开销，此操作仅针对种群最佳工件排序实施。

4）基于Taillard 加速算法［22］计算最大完工时间，以节约计算开销、提高算法的运行效率。

针对个体最佳工件排序（i=1，2，…，n）的局部搜索方法为：如果个体历史最优解pi连续M次迭代没有得到改善，则执行交换操作以产生扰动；然后进行解构、构造和局部搜索操作，如果新的工件排序更优，则更新。基于Matlab 的伪代码如下：

输入表示个体历史最优解pi对应的工件排序；d表示在解构阶段去除工件的个数；

输出。

其中，第2）行计算个体最优解pi未得到改善的连续迭代次数；第3）～5）行为交换操作；第7）行为解构；第8）行为带TBLJP1机制的构造；第9）～12）行为带TBLJP1机制的局部搜索；第13）～15）行为新解的接受。

针对种群最佳工件排序π*的局部搜索方法为：如果种群历史最优解g连续M次迭代没有得到改善，则基于交换邻域产生扰动，然后执行一轮（n次）d=1 的解构、构建操作，如果新的工件排序更优，则更新π*，并执行下一轮的解构、构建，综合考虑优化效果及计算开销，解构和构建操作最多执行K轮。具体步骤如下：

输入π*表示种群历史最优解g对应的工件排序；K表示解构和构建操作最多执行K轮；

输出π*。

其中，第2）行计算种群最优解g未得到改善的连续迭代次数；第3）～5）行为交换操作；第8）～15）行为一轮解构、构建操作（带TBLJP1机制），第17）行为新解的接受。

2.2.4 计算复杂度分析

算法主要的计算开销是对个体适应度值的计算，主要集中在算法迭代阶段，因此忽略种群初始化阶段的计算开销。算法每迭代一次，在更新鸟群的位置之后需要重新评估所有个体，计算复杂度为O(N×mn)；对个体的最佳工件排序进行局部搜索，计算复杂度为O(N×d×mn+N×mn2)；对种群最佳工件排序进行局部搜索，计算复杂度为O(3K×mn2)。因此，算法G次迭代的计算复杂度为：O(G× (N× (1 +D) ×mn+(3K+N) ×mn2))。可见，整个算法的计算复杂度并不算高。这主要得益于以下两点：1）局部搜索基于Taillard 加速算法求解完工时间，能够有效降低算法的计算复杂度；2）在对个体最佳工件排序的局部搜索中，仅基于交换邻域产生扰动，并不对新产生的个体进行评估，可节省的计算复杂度为，即通过合理的算法设计降低了计算复杂度。此外，也可以看出，在问题规模确定的情况下，算法的计算复杂度主要取决于参数G、K、N。

3 实验与分析

3.1 实验环境及参数设置

实验仿真环境为：Windows 10 操作系统、主频3.6 GHz的CPU、8.0 GB 的内存，编程语言及版本为Matlab R2019b。参数设置为：N=100，G=1 000，C=S=1.5，a1=a2=1，P∈[0.8，1]，FL∈[0.5，0.9]，FQ=3，T0=100，Tf=1，β=0.9，M=5，K=n/5，d=3。

为了测试算法的有效性，基于广泛使用的Rec 标准测试集进行验证，表1 给出了Rec 标准测试集中各算例的已知最优解，具体的测试算例可通过OR-LIBRARY 获取，每个算例均独立运行20 次。以最佳相对误差（Best Relative Error，BRE）和平均相对误差（Average Relative Error，ARE）为指标进行比较，计算公式如下：

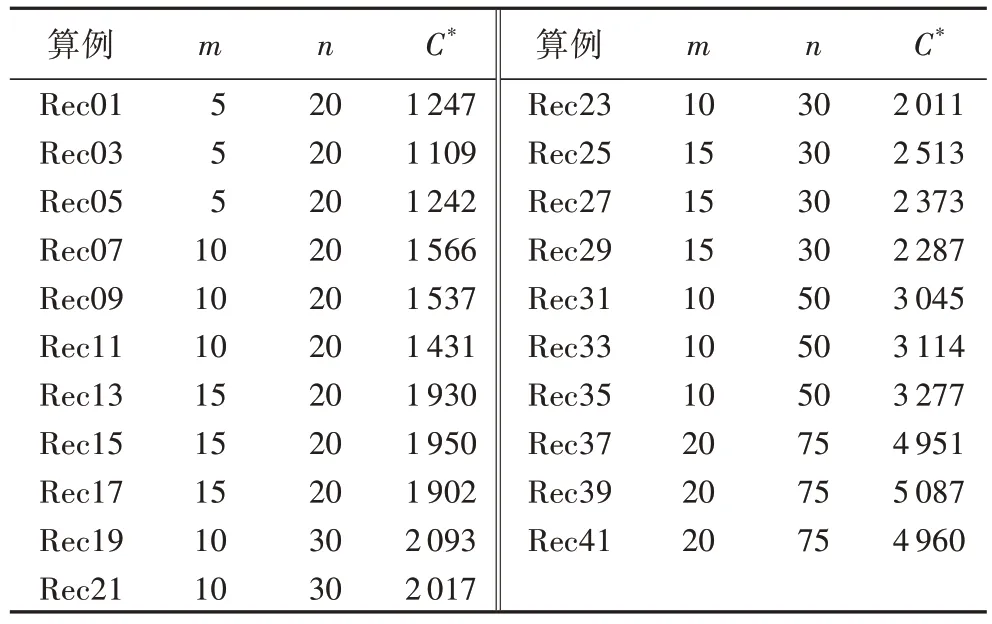
表1 Rec标准测试集的最优解Tab.1 The optimal results of Rec benchmark

3.2 算法比较

用HBSA1 表示BSA 和种群初始化方法的组合；用HBSA2 表示BSA、种群初始化方法及对个体最佳工件排序进行局部搜索的组合；HBSA3 表示BSA、种群初始化方法及对种群最佳工件排序进行局部搜索的组合。为了验证改进工作的有效性，针对Rec 标准测试集，将HBSA 与BSA、HBSA1、HBSA2 和HBSA3 进行比较。表2 给出了比较结果。

表2 HBSA与BSA、HBSA1～HBSA3计算结果的比较Tab.2 Comparison of computational results among HBSA，BSA and HBSA1～HBSA3

图5 给出了HBSA 和BSA 对Rec07、Rec17、Rec27 和Rec37 的收敛曲线。从图5 可以看出，对于上述所有的算例，HBSA 的初始值、收敛的速度和精度都明显优于BSA。这是因为在种群初始化阶段，HBSA 结合NEHLJP1 启发式算法产生10%的个体、使用混沌映射生成剩余的个体，使得初始种群拥有更好的初始值和较好的多样性，算法迭代的效率更高；对个体最佳工件排序和种群最佳工件排序进行局部搜索则增强了算法对解空间的探索能力，并能在一定程度避免陷入局部最优，从而使算法具有更高的收敛速度和收敛精度。综上所述，比较结果表明：提出的改进措施大幅度地提高了算法收敛的速度和精度，有效提高了算法的性能。

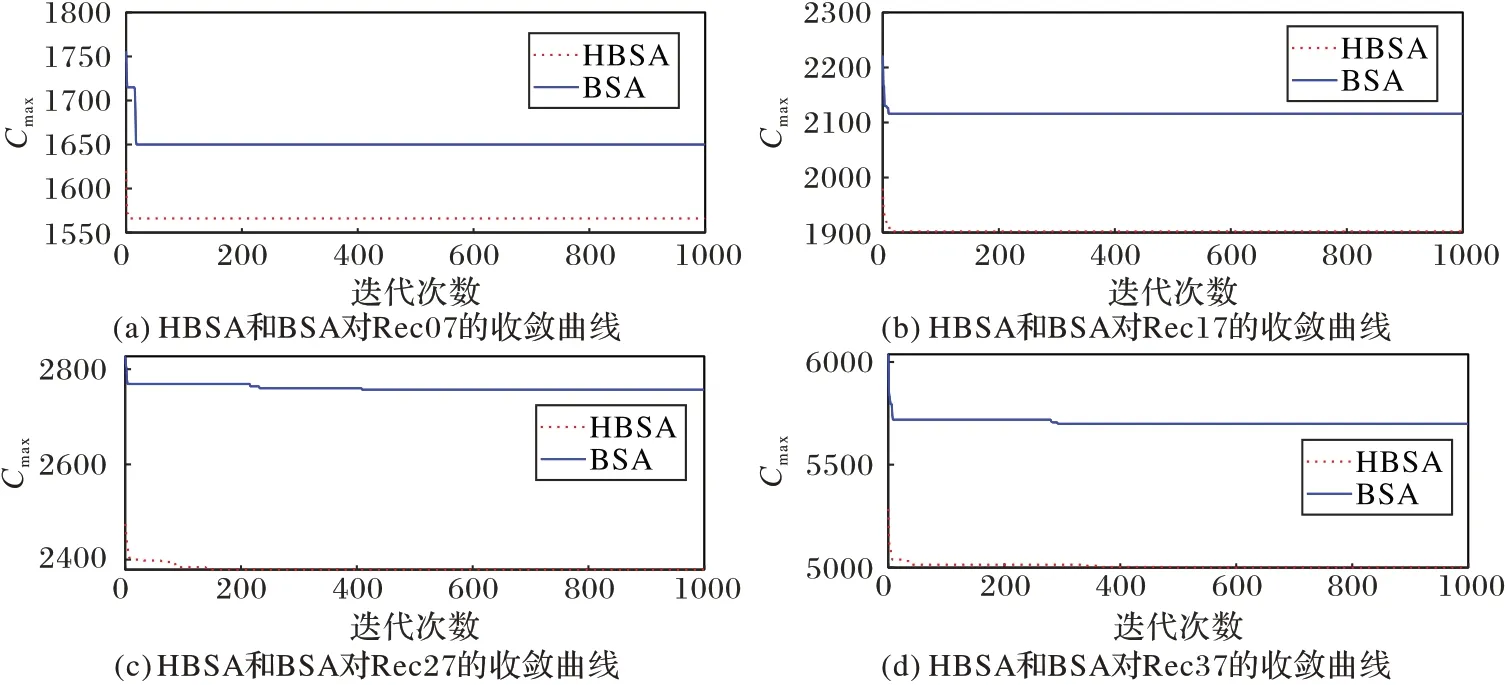
图5 HBSA和BSA对Rec07、Rec17、Rec27及Rec37的收敛曲线Fig.5 Convergence curves of HBSA and BSA for Rec07，Rec17，Rec27 and Rec37

为了进一步验证HBSA 的性能，将计算结果与以下4 种优化算法相比较：1）混合差分进化算法（L-HDE）［7］；2）混合共生生物搜索算法（HSOS）［9］；3）离散狼群算法（Discrete Wolf Pack Algorithm，DWPA）［23］；4）多班级教学优化（Multi-Class Teaching-Learning-Based Optimization，MCTLBO）算法［24］。

表3 给出了计算结果的比较。

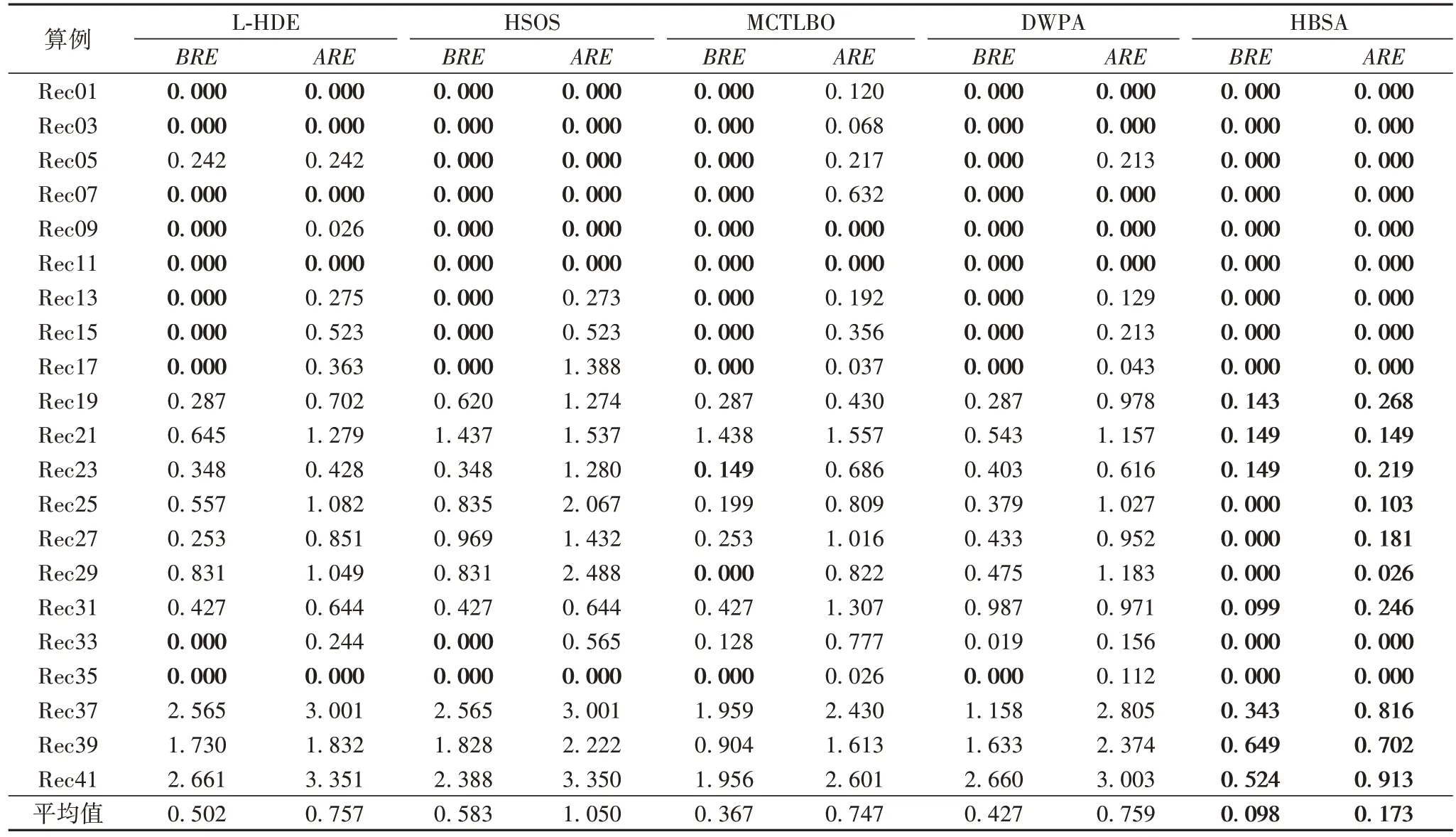
表3 HBSA与四种优化算法计算结果的比较Tab.3 Comparison of computational results among HBSA and four optimization algorithms

图6 给出了HBSA 与L-HDE、HSOS、MCTLBO 及DWPA取得的BRE的比较。

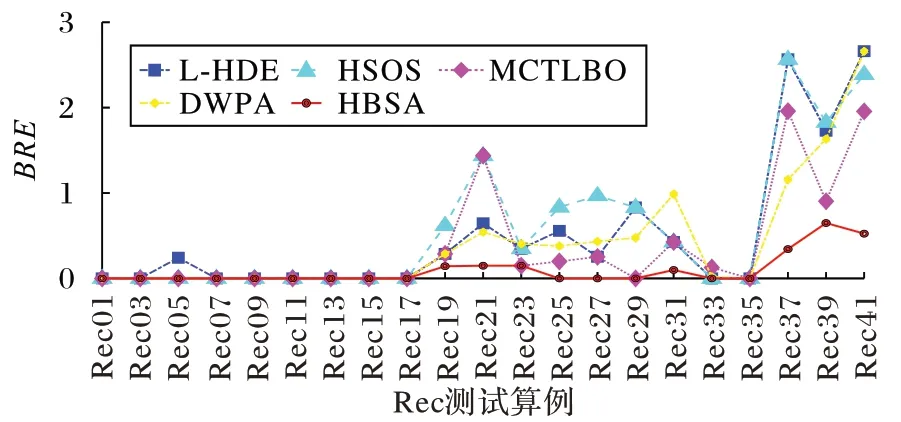
图6 BRE的比较Fig.6 Comparison of BRE

从图6 中可以看出，HBSA 取得了所有（共21 个）测试用例的BRE的最优值、排名第一；其次是MCTLBO，取得了12个最优值；然后是HSOS，取得了11 个最优值，最后是L-HDE和DWPA，均取得了10 个最优值，从而证明了HBSA 的寻优能力优于上述四种算法。

图7 给出了HBSA 与L-HDE、HSOS、MCTLBO 及DWPA取得的ARE的比较，同样地，HBSA 取得了所有测试用例ARE的最优值、排名第一；其次是HSOS，取得了7 个最优值；然后是L-HDE 和DWPA，均取得了5 个最优值；最后是MCTLBO，取得了2 个最优值，从而证明了HBSA 的稳定性强于上述四种算法。

图7 ARE的比较Fig.7 Comparison of ARE

针对不同规模测试算例求得的BRE和ARE的平均值，HBSA 取得的结果分别为0.098 和0.173，相比L-HDE 的0.502 和0.757、HSOS 的0.583 和1.050、MCTLBO 的0.367 和0.747、DWPA 的0.427 和0.759，和至少下降了73.3%和76.8%，可见，HBSA 优化结果较其他算法提升很明显。各算法针对不同规模测试算例求得的BRE和ARE的平均值的比较如图8 所示。

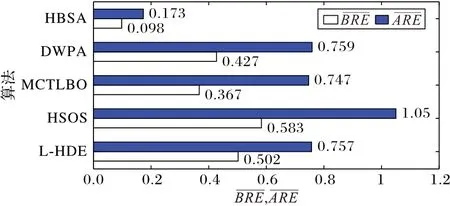
图8 和的比较

值得说明的是，针对Rec25 和Rec27，仅HBSA 的计算结果达到了目前已知最优解，从而进一步证明了HBSA 的优越性。HBSA 求得Rec27 的最佳工件排序为：π*=［17，11，28，10，4，30，16，29，19，9，25，3，23，21，18，20，24，6，1，12，2，22，27，8，5，26，14，13，7，15］；求得Rec25 的最佳工件排序并不唯一，其中一个工件排序为：π*=［21，29，2，18，4，24，5，16，26，22，28，30，11，20，19，1，9，10，7，14，27，6，23，15，13，12，3，25，17，8］。

4 结语

本文针对以最大完工时间最小化为目标的置换流水车间调度问题（PFSP），提出了一种混合鸟群算法（HBSA）进行求解。结合NEHLJP1 启发式算法和混沌映射提出了一种新的种群初始化方法，以改善初始种群的质量和多样性；采用LRV 规则将连续的位置值转换为离散的工件排序，从而使算法能够处理离散的调度问题；借鉴VNS 和IG 算法的思想针对个体最佳工件排序和种群最佳工件排序分别提出了局部搜索方法，以强化算法对解空间的探索能力。针对Rec 标准测试集进行了仿真测试，根据最佳相对误差和平均相对误差进行比较，结果显示提出的改进措施大幅度地提高了BSA 收敛的速度和精度，有效地提升了BSA 的性能；此外，HBSA 的表现也明显优于L-HDE、HSOS、MCTLBO 及DWPA 等算法，具有更强的全局寻优能力和更好的稳定性，尤其是针对Rec25 和Rec27 测试算例，仅HBSA 的计算结果达到了目前已知最优解，进一步证明了HBSA 的优越性，从而为解决置换流水车间调度问题提供了一种更加有效的方法。未来将在大规模地置换流水车间调度问题、其他调度目标的优化及多个调度目标的协同优化等方面做进一步的研究。