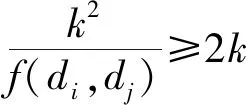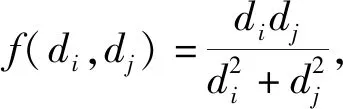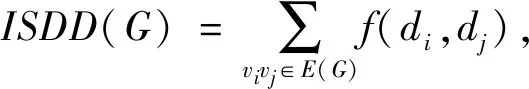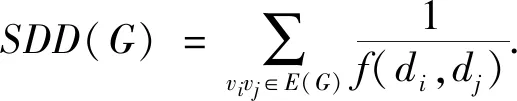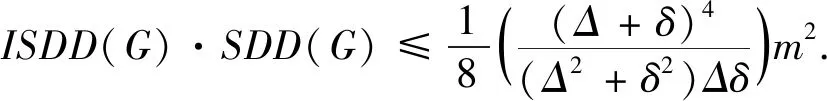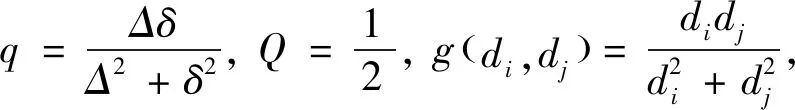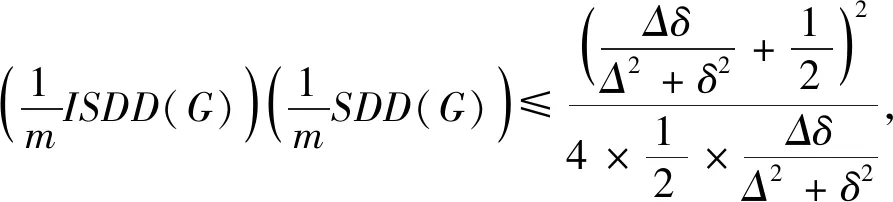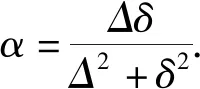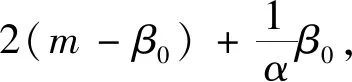图的ISDD指数的界
2022-09-24邵燕灵
程 宇,邵燕灵
(中北大学 理学院,山西 太原 030051)
0 引 言
本文所考虑的图均为简单无向图.设图G=(V(G),E(G))为n阶m条边的无向图,其顶点集为V(G)={v1,v2,…,vn},边集为E(G),且|E(G)|=m.di为顶点vi的度,i=1,2,…,n.图G的最大度记为Δ,最小度记为δ.

图G的反对称分割指数[7](ISDD指数)是由Ghorbani等在2021年提出的一个新分子拓扑指数,其被定义为
文献[7]给出ISDD(G)和SDD(G)的一些上、下界,并给出ISDD(G)和SDD(G)之间的不等式关系,还证明了在顶点数为n的树中,星图的ISDD(G)值最小,路图的ISDD(G)值最大.
本文还用到了其他拓扑指数,包含遗忘指数[8]
第二萨格勒布指数[9]

第一萨格勒布指数[11]
本文利用一些已知的不等式给出了ISDD(G)的一些上、下界,得出了ISDD(G)和SDD(G)之间的关系,并证明了在一定条件下ISDD(G)和SDD(G)是线性相关的.
1 预备知识
引理 1[12]设x1,x2…xn为正实数,则
当且仅当x1=x2=…=xn时,等式成立.
引理 2[13](柯西-施瓦兹不等式) 设ai,bi∈R,1≤i≤n,则
当且仅当对于任意的1≤i,j≤n,aibj=ajbi时,等式成立.
引理 3[14]设ak,bk≥0,且0<ωbk≤ak≤Ωbk,1≤k≤m,则
当且仅当ω=Ω和ak=ωbk时,等式成立.
引理 4[15]设0 根据已知的不等式得出了ISDD(G)指数的一些上、下界. 定理 1设G是边数为m,最大度为Δ,最小度为δ的图,则 (1) 当且仅当G为二部半正则图或正则图时,式(1) 左边等号成立,当且仅当G为正则图时,式(1) 右边等号成立. (2) 当且仅当di=δ,dj=Δ时,式(2)左边等号成立,当且仅当di=dj时,式(2)右边等号成立.故 当且仅当G为二部半正则图或正则图时,左边等号成立,当且仅当G为正则图时右边等号成立.证毕. 定理 2设G是边数为m,最大度为Δ,最小度为δ的图,则 (3) 当且仅当G为正则图时,式(3)等号成立. 证明根据引理1可得 故 当式(3)等号成立时,对于任意一条边vivj∈E(G),didj=δ2,di=dj,即di=dj=δ,所以,G为正则图. 反之,当G为正则图时, 证毕. 定理3设G是边数为m,最大度为Δ,最小度为δ的图,则 (4) 当且仅当G为正则图时,式(4)等号成立. 证明根据引理1可得 故 反之,当G为正则图时, 证毕. 定理 4设G是边数为m,最大度为Δ,最小度为δ的图,则 (5) 当且仅当G为正则图时,式(5)等号成立. 证明注意到 因为 (6) 故 同理,能得出 反之,当G为正则图时, 证毕. 定理 5设G是边数为m,最大度为Δ,最小度为δ的图,则 (7) 当且仅当G为正则图时,式(7)等号成立. 证明根据引理2可得 又由式(6)可得 反之,当G为正则图时, 证毕. 定理 6设G是一个边数为m,最大度为Δ,最小度为δ的图,则 (8) 当且仅当G为正则图时,式(8)等号成立. 证明假设 根据式(2)可得 因为 可得 根据引理3等式成立的条件,可得 易得di=Δ=δ,所以,G为正则图. 反之,当G为正则图时, 另一方面, 所以 (9) 反之,当G为正则图时, 证毕. 给出ISDD(G)和SDD(G)之间的不等式关系,并证明了在一定情况下,ISDD(G)指数和SDD(G)指数是线性相关的. 引理 5设f和k为任意正实数,则 证明因(f-k)2≥0,故 f2-2kf+k2≥0,f2+k2≥2kf, 证毕. ISDD(G)+k2SDD(G)≥2km. 故 ISDD(G)+k2SDD(G)≥2km. 证毕. 定理 8设G是一个边数为m,最大度为Δ,最小度为δ的图,则 (10) 当G为正则图时,式(10)等号成立. 证明记 0 代入引理4可得 因此 当G为正则图时,有 ISDD(G)·SDD(G). 证毕. 故 αSDD(G). 证毕.2 ISDD(G)指数的界




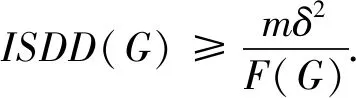
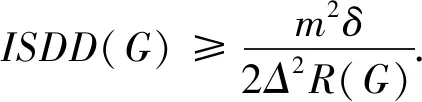


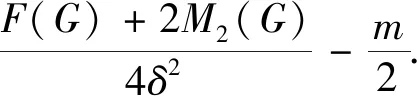
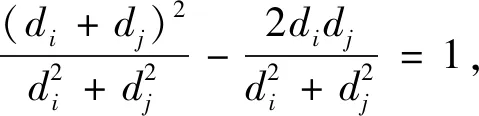
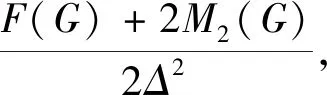

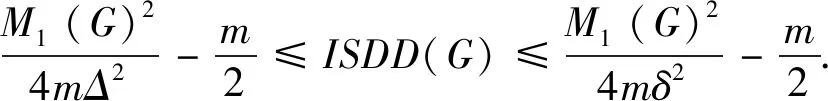

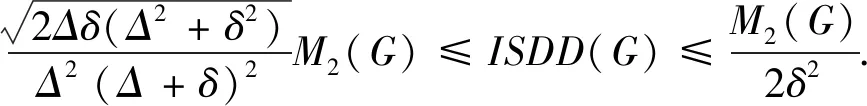

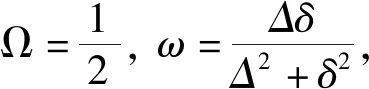

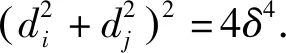
3 ISDD(G)和SDD(G)之间的联系