一类带组合记忆项的Tricomi方程解的破裂

任 翠，明 森，韩 伟，杜嘉仪

(中北大学 理学院，山西 太原 030051)

0 引 言

本文研究带组合记忆项的Tricomi方程的Cauchy问题

(1)

本文利用迭代方法研究问题(1)解的破裂性态，将文献[4]中研究的带组合非线性项的问题推广为带组合记忆项的Tricomi方程小初值问题.同时，分别将文献[5,10]中研究的带幂次记忆项的Tricomi方程与波动方程推广为带组合记忆项的Tricomi方程，并给出解的生命跨度的上界估计.

定理 1设θ(n,l,p,q)=3+r-((1-n(l+1))(p/2)+(r+(n-1)(p-1))(l+1)+n)(q-1)>0.

suppu⊂{(t,x)∈[0,T)×Rn‖x|≤R+φl(t)},

其中,φl(t)=tl+1/(l+1).则存在正数ε0=ε0(n,l,p,q,u0,u1,R)，使得问题(1)的解有生命跨度的上界估计，即

(2)

式中：0<ε≤ε0；C为不依赖于ε的正常数.

本文给出定理1证明过程中需用到的一些引理以及对问题(1)弱解的定义.

引理 1[4]设φ(x)满足

式中：Sn-1表示n-1维球面.设

λ(t)=Clt1/2K1/(2l+2)((l+1)-1tl+1)>0,

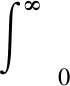
ψtt-t2lΔψ=0.

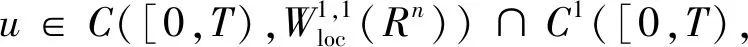
且满足

|u(s,x)|q)ψ(s,x)dsdxdτ,

(3)

|u(s,x)|q)ψ(s,x)dsdxdτ.

(4)

1 定理1的证明

记

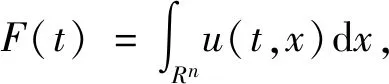
(5)

(6)

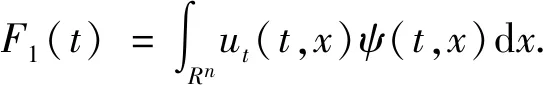
(7)

首先，分别建立F0(t)与F1(t)的估计.

引理 2设u0,u1满足定理1的条件，存在T0>0，对∀t∈[2T0,T)，则

F0(t)εIl[u0,u1]t-l,

(8)

其中

(9)

证明将ψ(t,x)=λ(t)φ(x)代入式(3)，利用λ(0)=1，可知

ψ(s,x)dsdxdτ=εIl[u0,u1]+

ψ(s,x)dsdxdτ.

计算得到

ψ(s,x)dsdxdτ.

(10)

于是

(11)

式(11)两端同乘(λ(t))-2，并在[0,t]区间积分，可得

(12)

因此

由于

则有

F0(t)εIl[u0,u1]t-le-2φl(s)sle2φl(s)ds.

因此，对于∀t∈[2T0,T)，可知

F0(t)εIl[u0,u1]t-le-2φl(t)sle2φl(s)ds

εIl[u0,u1]t-l(1-e-2φl(t/2)-2φl(t))=

εIl[u0,u1]t-l(1-e2(2-(l+1)-1)φl(t))

εIl[u0,u1]t-l.

引理2证毕.

引理 3设u0,u1满足定理1的条件，存在T0>0，对∀t∈[2T0,T)，有

F1(t)εIl[u0,u1].

证明令

则有F1(t)=λ(t)F4(t).在式(4)中令ψ(t,x)=φ(x)，可得

(|ut(s,x)|p+|u(s,x)|q)φ(x)dsdxdτ=

φ(x)dsdxdτ.

(13)

由于F0(t)≥0，∀t∈[0,T)，则式(13)表明F4(t)≥0，于是F1(t)≥0.由式(6)与式(7)可知

(14)

利用式(10)可得

(15)

将式(15)关于t求导，得

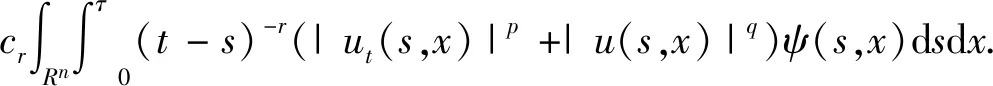
结合式(14)可得

则有

(16)

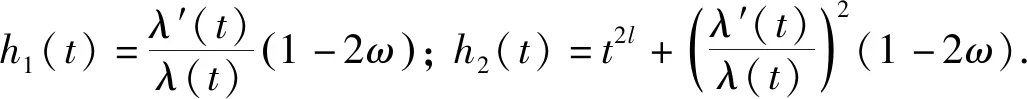
(17)

结合式(15)～式(17)，得

(18)

式(18)两端同乘(λ(t))-2，并在[0,t]上积分可得

从而

εIl[u0,u1](1-e-2ω(1-2-(l+1))φl(t))

εIl[u0,u1].

引理3证毕.

在式(3)中令ψ(t,x)=1，可得

(|ut(s,x)|p+|u(s,x)|q)dsdxdτ，

则有

(|ut(s,x)|p+|u(s,x)|q)dsdxdτ.

(19)

式(19)在[0,t]上积分，可知

F(t)=

(|ut(η,x)|p+|u(η,x)|q)dηdsdxdτ.

于是

|u(η,x)|q)dηdsdxdτ.

(20)

根据式(20)得

(21)

利用Hölder不等式可知

Fq(η)(R+η)-n(q-1).

于是

(22)

根据式(20)可知

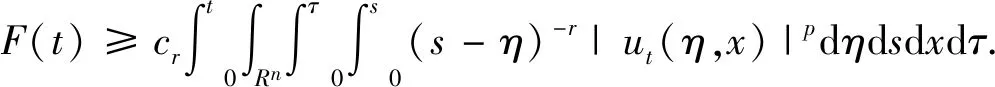
(23)

计算得到

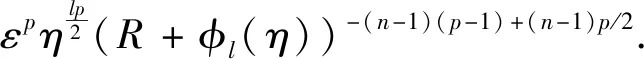
(24)

从而

φl(η))-(n-1)(p-1)+(n-1)p/2dηdsdτ.

(25)

将式(25)在(2T0,t)区间积分，有

ηlp/2(R+φl(η))-(n-1)(p-1)+(n-1)p/2-rdηdsdτ≥

φl(η))(n-1)p/2dηdsdτ≥Kεp(R+t)(-r-(n-1)(p-1))(l+1)·

(t-2T0)(n-1)(l+1)p/2+lp/2+3.

(26)

下面利用迭代方法给出解的生命跨度的上界估计.

假设

(27)

基于式(26)，当j=0时，有

C0=Kεp,α0=(r+(n-1)(p-1))(l+1),

β0=(n-1)(l+1)p/2+lp/2+3.

(28)

将式(27)代入式(22)，可知

F(t)≥

Cj+1(R+t)-αj+1(t-2T0)βj+1,

(29)

其中

αj+1=αjq+n(q-1)+r,βj+1=βjq+3.

(30)

从而得到

αj=qαj-1+n(q-1)+r=

(α0+n+r/(q-1))qj-n-r/(q-1),

(31)

βj=βj-1q+3=(β0+3/(q-1))qj-3/(q-1).

(32)

于是

(βjq+1)(βjq+2)(βjq+3)≤(βjq+3)3=

(33)

则有

从而

logCj≥logM-3jlogq+qlogCj-1≥

(1+q)logM-3(j+(j-1)q)logq+q2logCj-2≥

当j≥j0时，有

计算可知

qjlog(Kεpq-3q/(q-1)2M1/(q-1))=qjlog(Dεp),

(34)

式中：D=Kq-3q/(q-1)2M1/(q-1).利用式(24)、式(31)、式(32)与式(34)，可以得到

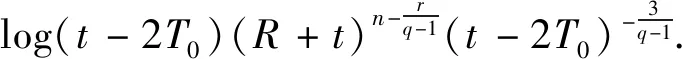
(35)

当t≥T1=max{R,4T0}时，则有log(R+t)≤log(2t),log(t-2T0)≥log(t/2).于是

F(t)≥exp(qj(log(Dεp)+

(36)

其中

定理1证毕.