基于自适应樽海鞘算法的多无人机任务分配

张森悦, 隋学梅, 李一波

(1. 沈阳航空航天大学 人工智能学院, 沈阳 110136; 2. 沈阳航空航天大学 自动化学院, 沈阳 110136)

随着无人机(unmanned aerial vehicle, UAV)发展的日渐完善, 其在相关领域中的应用越来越广泛. 为弥补单一无人机作战缺陷, 多无人机协同系统已逐渐成为主流. 针对多无人机协同任务分配问题, 目前已有许多研究成果, 如混合整数线性规划[1]、 多旅行商[2]、 多UAV协同任务分配(cooperative multiple task assignment problem, CMTAP)[3]等模型, 其中CMTAP模型适用于求解UAV执行有序任务的问题. 目前任务分配算法主要分为两类： 进化和群智能算法. 遗传算法(genetic algorithm, GA)[3-4]是最经典的进化算法, 其通过交叉和变异算子求解问题[5-6], 但算法易陷入早熟. 群智能算法是模仿生物的行为特点而产生的启发式寻优算法, 其中较经典的有蚁群算法[7]、 人工蜂群算法[8]、 粒子群优化算法(particle swarm optimization, PSO)[9]等. 但这些算法也有易陷入局部最优解、 初期收敛速度慢、 运行时间长等缺点. 近年来, 如灰狼优化算法[10-12]、 蝗虫优化算法[13-14]、 鲸鱼算法[15-16]等新兴仿生算法相继被提出, 但研究表明, 这些算法仍存在种群多样性差、 收敛精度低的问题.

Mirjalili等[17]根据樽海鞘种群在海洋内集群觅食的行为特点提出了樽海鞘算法(salp swarm algorithm, SSA) , 该算法将樽海鞘链分为领导者和跟随者, 领导者是整个链的头部, 跟随者是整个链的尾部. 领导者一直向食物方向移动, 跟随者紧跟领导者. 模拟这种生物的捕食方式, 提出了樽海鞘算法解决寻优问题, 并已成功应用于各领域[18-20]. 经典的SSA算法用于解决连续域的优化问题, 但却无法解决离散问题. Walaa等[21]提出了一种改进的樽海鞘算法(modified salp swarm algorithm, MSSA), 将该算法应用于解决任务分配问题, 并通过实验验证了该算法相对于其他算法具有明显的优势. 与其他群智能算法类似, 樽海鞘算法也易陷入局部最优解[22-23].

针对MSSA算法存在易陷入局部最优的缺陷, 本文提出一种用于解决多无人机任务分配问题的自适应樽海鞘算法(self-adaptive modified salp swarm algorithm, SA-MSSA). 该算法修改了樽海鞘领导者位置更新公式, 在其中考虑每一代的父代位置和食物源对子代位置更新的影响. 同时为提高算法前期的全局搜索能力, 在算法中考虑加入自适应算子, 动态调整前后期每一代需要的领导者和跟随者的比例. 仿真实验结果表明, 本文算法具有脱离局部最优的能力, 提升了收敛性能和求解速度, 适应度也大幅度提高, 成功解决了多无人机的任务分配问题.

1 CMTAP模型建立

1.1 模型描述

假设共有m架无人机U={U1,U2,…,Um},n个作战目标T={T1,T2,…,Tn}, 每个目标需要依次完成侦查、 攻击和评估3个任务,MT={Classify(C),Attack(A),Verify(V)}[24],NT为任务数量, 这里NT=3×n.一般情况下假设n≠m, 分配目的是通过合理安排, 使m架UAV以最小的代价完成NT个任务.

1.2 约束条件

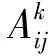
(1)

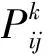
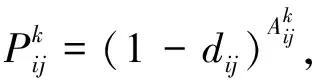
(2)

其中dij为优势概率.无人机i和目标j的相对距离Dij表示为

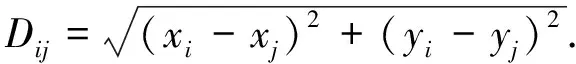
(3)

无人机i和目标j的相对速度Vij表示为

Vij=|Vicosθi+Vjcosθj|.

(4)

任务数量约束： 任务数量约束确保每个目标的每个任务都被执行, 可表示为

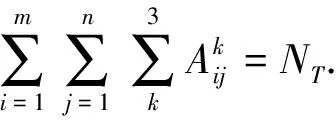
(5)

任务时序约束： 任务时序约束确保目标j按照侦查、 攻击、 评估的顺序执行, 可表示为

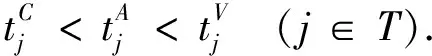
(6)

1.3 评价指标

CMTAP模型的目标函数是构建执行代价函数J1和时间代价函数J2, 执行代价是无人机对目标作战时的损耗, 时间代价是完成所有任务所需的时间.

1.3.1 执行代价

用J1表示无人机i执行目标j的任务k时的执行代价, 可表示为

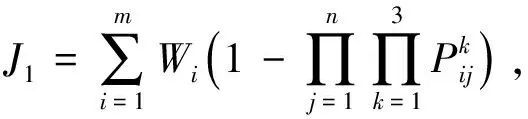
(7)

其中Wi表示损伤代价.

1.3.2 时间代价

用J2表示执行任务结束的时间代价, 以执行最后一个任务的无人机为整个团队的时间, 时间代价的单位为s, 可表示为

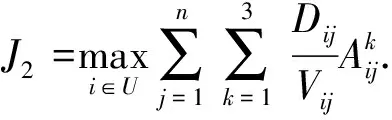
(8)

1.3.3 总体目标函数

总体目标函数可表示为

minJ=J1+J2,

(9)

服从于

(10)

总体目标函数约束满足式(1),(5)，(6),(10), 目标函数表示执行代价和时间代价最小, 约束条件(10)确保一个任务只由一架无人机完成.

2 算法设计

2.1 经典樽海鞘算法

樽海鞘算法[17]是模拟海洋生物樽海鞘的种群移动规律提出的, 要将该算法用于CMTAP求解[25], 可将樽海鞘链中的一个樽海鞘视为一个求解方案, 食物源表示当前最好的分配结果, 确定合适的编码方法, 然后通过领导者与跟随者位置更新等操作不断生成新的种群, 直到满足约束条件.

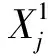
(11)

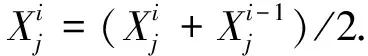
(12)

若食物源定义为Fj(j=1,2,…,N), 范围的上下界分别为ubj和lbj,c1,c2和c3是影响位置更新的系数, 则

c1=2exp{-(4l/L)2},

(13)

其中c2和c3为[-1,1]内的随机数,l表示当前迭代次数,L表示最大迭代次数.

樽海鞘算法寻优是通过位置更新迭代完成的, 式(11)更新领导者的位置, 式(12)更新跟随者的位置, 整体向最优解(食物源)迭代.移动过程中, 领导者进行全局探索, 而跟随者则进行局部探索, 直到终止.

2.2 自适应樽海鞘算法

为提高多无人机任务分配的收敛速度并克服陷入局部最优的问题, 本文将樽海鞘算法和自适应算子相结合, 提出一种自适应樽海鞘算法.

图1 编码方式Fig.1 Method of coding

2.2.1 种群初始化

SA-MSSA算法的种群采用实数编码的方式[26], 编码长度为任务数目n.假设系统中有4架无人机、 6个任务, 则其中一种编码方式如图1所示.

2.2.2 位置更新

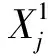
1) 领导者.在MSSA算法中, 领导者寻优过程若一开始就向全局最优移动, 则可能导致全局寻优不全面, 也易陷入局部最优和收敛速度低的问题[21]. 本文将领导者位置更新公式修改为

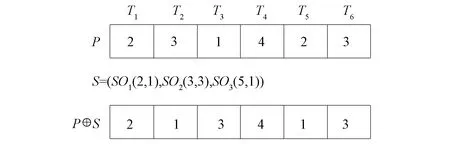
图2 P⊕S示例Fig.2 Example of P⊕S

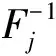
符号⊕的计算过程如图2所示.例如：

符号⊖的计算过程如图3所示, 具体流程如图4所示, 其结果与优势概率有关, 例如：

P1⊖P2=(SO1(2,3),SO2(3,3),SO3(5,1)).

图3 P1⊖P2示意图Fig.3 Schematic diagram of P1⊖P2

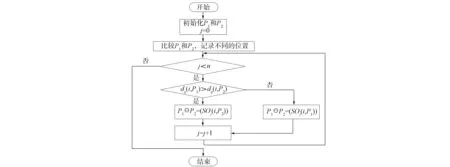
图4 P1⊖P2流程Fig.4 Flow chart of P1⊖P2

2) 跟随者.跟随者位置按下式进行更新:

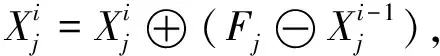
(16)

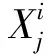
2.2.3 自适应算子

MSSA算法迭代时, 种群的领导者固定为1, 其余为跟随者[21], 会导致算法前期全局搜索能力不足, 后期局部搜索缓慢, 从而降低算法的整体精度. 针对此问题, SA-MSSA算法引入了自适应算子[27], 使领导者和跟随者的比例随迭代过程变化, 前期领导者较多, 后期跟随者较多, 自适应算子中领导者的百分比r根据

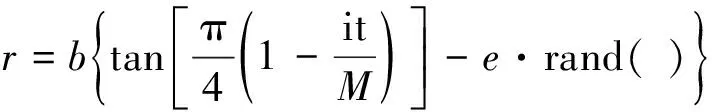
(17)

进行计算, 跟随者的百分比为1-r.其中:b为比例系数, 避免两者比例偏差过大,e为扰动因子, 经过实验,b=0.75,e=0.2较合适; rand函数为(0,1)之间的随机数, 结合e对r进行扰动; it为算法当前迭代次数;M为算法最大迭代次数.

3 算法流程

本文提出的自适应樽海鞘算法处理流程如图5所示.

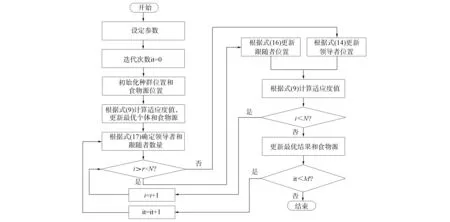
图5 SA-MSSA算法流程Fig.5 Flow chart of SA-MSSA algorithm

算法描述如下, 其中UAV数目设为m, 目标数目设为n, 迭代次数设为M, 种群数量设为N.

算法1SA-MSSA.

输入： UAV数目m, 目标数目n, 迭代次数M, 种群数量N;

输出： 最佳任务分配结果, 最优适应度(食物源F);

步骤1) it=0;

步骤2) 初始化种群和食物源的位置(无限大), 根据总体目标函数评估每个樽海鞘的适应度；

循环:

步骤3) 根据自适应算子公式确定领导者和跟随者数量;

步骤4) 根据跟随者和领导者的位置更新公式分别修改子代每个樽海鞘的位置, 生成新的樽海鞘种群;

步骤5) 重新评估目前种群的适应度, 更新食物源F和最佳任务分配结果;

步骤6) it=it+1;

直到it>M;

输出： 最佳任务分配结果和食物源F;

算法结束.

4 仿真与分析

实验所用计算机硬件配置为Intel Core(TM) i7-8750H CPU, NVDIA GeForce GTX 1060显卡和16 GB内存, 所有算法均在MATLAB R2018a平台编译运行. 为验证算法的性能, 本文设计3种不同场景, 分别为： 5架UAV和3个目标, 12架UAV和5个目标, 15架UAV和10个目标. 首先对本文SA-MSSA算法的性能进行分析, 然后用SA-MSSA算法、 MSSA算法、 PSO算法和GA算法分别求解3种场景下的分配问题, 将不同算法的实验结果进行分析对比. 各算法的参数设置列于表1, 其中Pc和Pm分别为GA算法的交叉和变异概率,c11和c12为PSO算法的学习因子[28-29].

表1 仿真参数设置

4.1 分配结果分析

UAV的作战区域为5 km×5 km[30], 5架UAV和3个目标, 不同属性信息分别列于表2和表3, 其中x和y分别表示无人机和目标的初始位置,θ为离轴角,V为速度,W为无人机的价值. 表4为无人机优势概率统计结果.

表2 UAV属性信息

表3 目标属性信息

表4 无人机的优势概率

针对上述数据, 采用基于SA-MSSA的UAV任务分配算法, 考虑实际的执行顺序列出任务分配结果如图6所示, 任务执行情况如图7所示. 由图6可见, 每个目标的3个任务都被执行. 由图7可见, 每架消防无人机都至少执行一个任务, 图中直线表示无人机执行任务的轨迹. 因此, 在该仿真场景下, SA-MSSA算法得到的任务分配结果可行. 最终的任务分配方案为UAV1：T1(C); UAV2：T2(V); UAV3：T1(A)→T3(V); UAV4：T3(C,A)→T1(V); UAV5：T2(C,A).

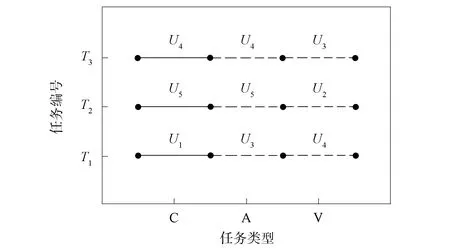
图6 任务分配结果Fig.6 Result of task assignment

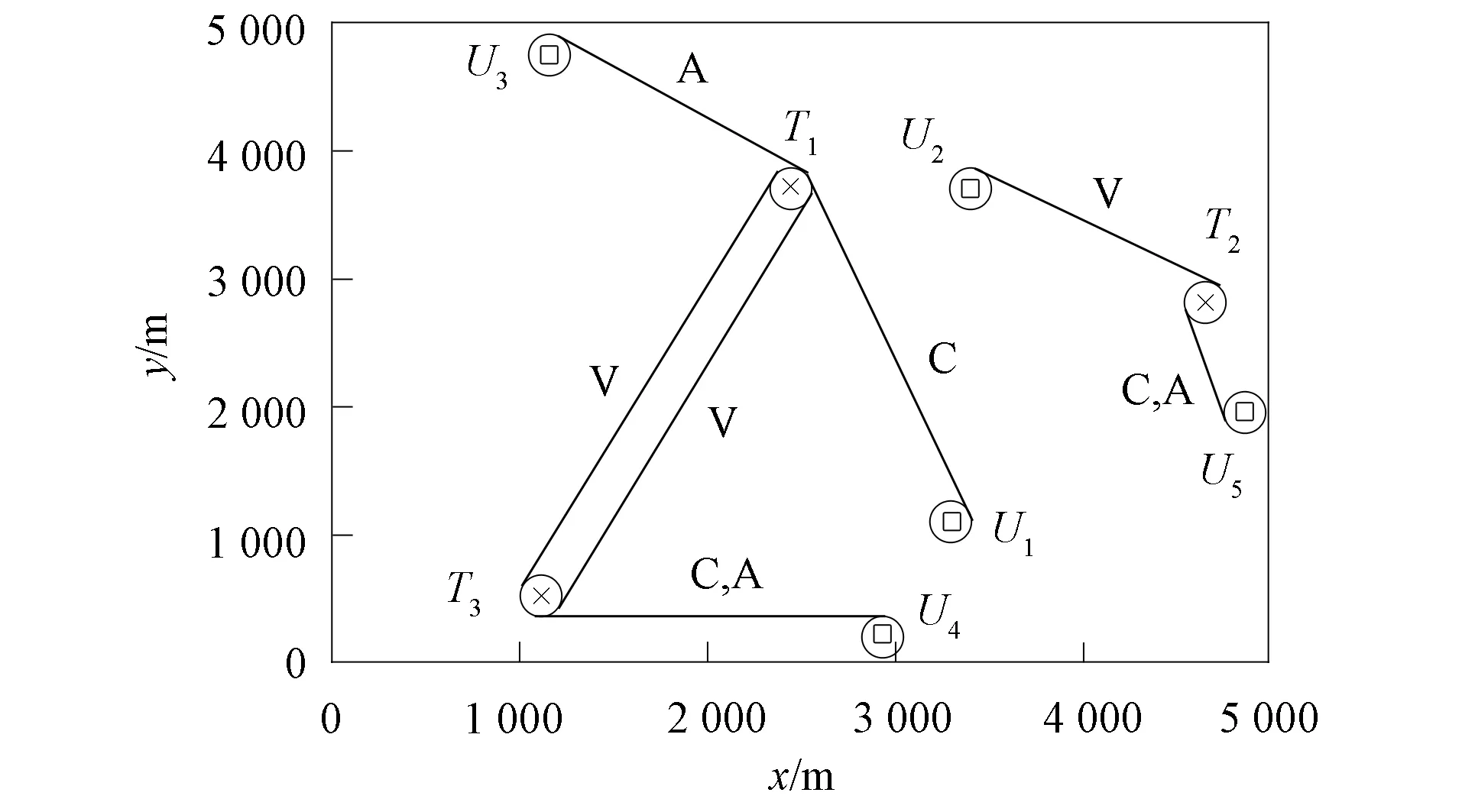
图7 任务执行情况示意图Fig.7 Schematic diagram of task execution

4.2 算法性能分析

为验证SA-MSSA算法求解CMTAP问题的能力, 本文将上述4种算法分别用于求解3种不同规模下的CMTAP问题, 所得结果列于表5. 其中, 规模S0503表示5架无人机和3个目标. 每种算法均进行10次实验, 并分别统计两种代价的3项指标： 最小值、 最大值和平均值.

表5 不同规模下4种算法的代价

由表5可见, SA-MSSA算法均获得了较好的结果, 而且随着规模变大, 算法的代价值也逐渐提高. 以S0503规模下4种算法的平均值为例, SA-MSSA算法的执行代价相比于GA提高了10.02%, 与PSO算法相比提高了3.8%, 与MSSA算法几乎一致； SA-MSSA算法时间代价相比于GA提高了96.58%, 与PSO算法相比提高了48.5%, 与MSSA算法相比提高了28.4%. 4种算法的适应度值列于表6.

表6 不同规模下4种算法的适应度值

续表6

由表6可见, 本文SA-MSSA算法在不同规模下都取得了最好的解, 适应度值最好. 以S0503规模下4种算法的适应度平均值为例, 本文算法相比于GA提高了93.2%, 与PSO算法相比提高了32.29%, 比MSSA算法提高了16.03%.

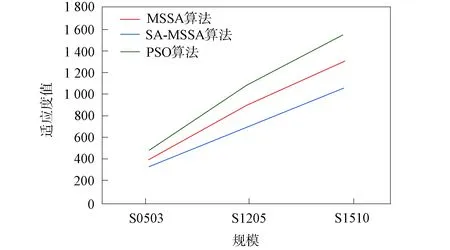
图8 不同规模下3种算法的平均适应度值变化曲线Fig.8 Change curves of average fitness values of three algorithms under different scales

实验结果表明, 当目标数量增加时, SA-MSSA算法获得的适应度值相对于其他算法的优势更明显, 代价更小. 这是因为当规模较小时, 解的空间分布集中, 表现出较大的分散性, 导致时间代价的收敛数值较大； 而求解更大规模时, SA-MSSA算法能增强种群在迭代后期的多样性, 增加可行解空间分布的多样性, 提高整个算法跳出局部最优的能力, 以更小的代价完成任务.

本文将PSO算法、 MSSA算法及SA-MSSA算法的平均适应度值进行对比, 结果如图8所示. 由图8可见, 随着问题规模的不断增大, 3种算法间的差异显著变大, SA-MSSA算法的优势更明显. 上述实验结果证明, 针对多无人机任务分配问题, 相对于GA算法、 PSO算法和经典樽海鞘算法, 本文提出的自适应樽海鞘算法的代价更小, 适应度更好.

4.3 算法收敛性分析

为验证SA-MSSA算法的收敛性, 使用4种算法在相同的仿真环境下迭代50次, 收敛曲线如图9所示(GA算法数值过大, 故图中未包含).

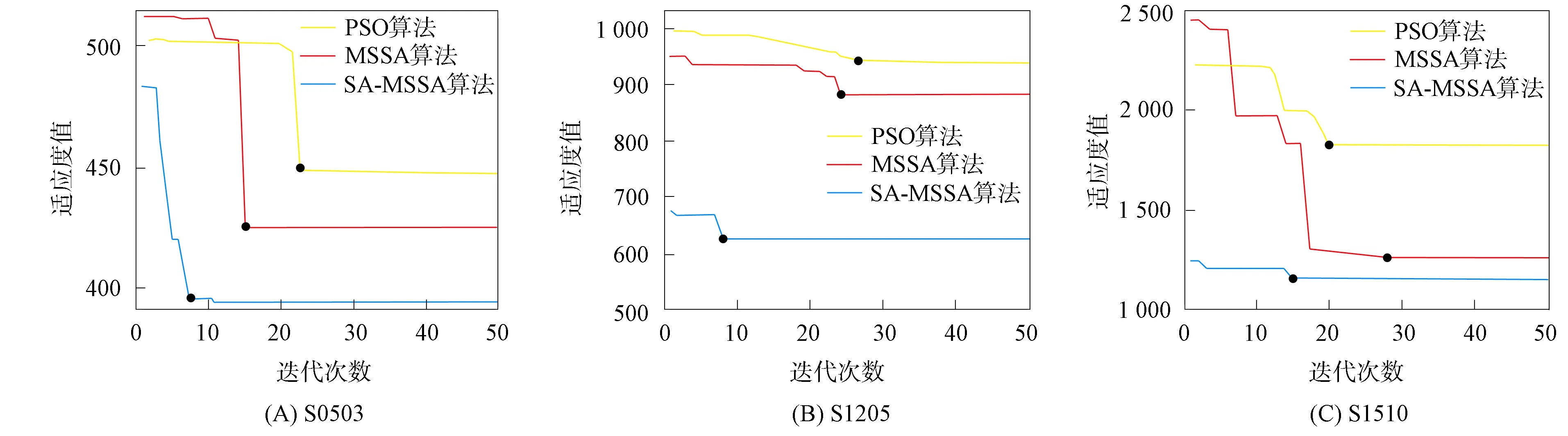
图9 不同规模下3种算法的收敛曲线对比Fig.9 Comparison of convergence curves of three algorithms under different scales

由图9可见, 无论何种规模下, SA-MSSA算法相比于PSO算法和MSSA算法代价均更小, 算法最后的收敛值更小, 收敛速度更快. 以S0503规模为例, 由图9(A)中可见, 相比PSO算法在23次迭代处收敛和MSSA算法在15次迭代处收敛, SA-MSSA算法提前到了在7次迭代处收敛.

综上所述, 针对多无人机任务分配问题, 本文基于樽海鞘算法, 提出了一种自适应樽海鞘算法. 首先, 修改了领导者位置更新公式, 使领导者受上一代领导者和最优解的影响; 然后, 在种群迭代更新过程中加入自适应算子, 动态调整领导者和跟随者的比例, 以提高前期的全局搜索和后期跳出局部极值的能力； 最后, 通过对4种算法的分配结果、 适应度及收敛曲线进行对比分析, 验证了本文算法在不同规模的无人机任务分配时均获得了更好的结果.