不同边界条件下道砟沉降及受力状态的离散元模拟研究

陈成，汪伦，张磊，芮瑞

(武汉理工大学 土木工程与建筑学院，湖北 武汉 430070)

随着我国近年来高速铁路的建设，对有砟轨道结构的结构安全及稳定性有了进一步的要求。由于道砟颗粒形状不规则、易破碎以及力学性能不均匀等特性，在自然条件和列车荷载下会导致大量基床病害，如轨枕不均匀沉降、道砟陷槽、道床脏污等，进而破坏列车行驶时的安全性及稳定性。因此，为了提高有砟轨道的安全性与稳定性，本文开展循环荷载作用下有砟轨道道床沉降的研究。道砟沉降的试验研究方面，SUN等[1-2]开展了一系列循环荷载三轴试验，研究了加载频率、轴重、围压对道砟变形及破碎的影响。MCDOW‐ELL等[3]进行了道砟箱加载试验，底部为橡胶板，侧边为刚性墙，研究了循环荷载作用下道砟的沉降规律，道砟沉降在初始阶段迅速增加，然后逐渐稳定。INDRARATNA等[4]采用大型PST装置，其侧边设置可横向位移的刚性板，研究了侧边围压对道砟沉降的影响。张徐等[5-6]开展了有砟轨道1︰1尺寸模型试验，获得不同加载条件下道床的变形及道砟的振动响应。曾志平等[7]进行了现场原位测试并建立轨道道床模型，研究了道床纵横向阻力的影响因素。以上试验多考虑道砟层沉降，受限于试验条件，并未考虑路基层沉降，并且采用试验研究无法在细观层面解释散粒体道床受循环荷载下的力学行为。因此，采用数值模拟方法可以弥补试验研究的不足。离散单元法通过计算颗粒间的接触力与颗粒位移来模拟离散体系内部的应力传递与变形发展。国内外学者多采用该方法模拟有砟道床的细观力学行为。LIM等[8]采用球形和非球形颗粒簇分别进行道砟箱加载试验模拟，发现由于颗粒间的咬合作用，非球形颗粒簇更接近真实道砟力学特性，并研究颗粒形状对颗粒内部不均匀应力的影响。LI等[9]采用不同级配层组成的道砟进行道砟箱模拟，发现使用双层道砟组合可以减小道砟层的沉降。CHEN等[10]进行了有、无侧限时加筋道砟在循环荷载作用下的模拟，结果表明在有、无侧限时轨枕沉降、颗粒运动情况均有差异。CHEN等[11]在大型道床模型试验的基础上使用离散元模拟来补充试验中缺乏的细观力学视角，模拟结果可较好地预测道砟在加载时的竖向位移与侧向位移趋势。FENG等[12]通过全尺寸道床高速加载试验和DEM仿真平台，对不同速度下全尺寸有砟道床的动态响应进行对比分析。徐旸等[13]基于激光扫描技术建立了离散元道砟模型，研究了在高速及重载条件下道砟级配对道床动力沉降特性的影响规律。综上，当前模拟循环荷载下的道床劣化的模型主要有2类：1)有侧限的道砟箱模型；2)无侧限的全尺寸有砟道床模型。在离散元模拟中，其计算速度与颗粒数量相关，因此全尺寸的道床模型会面临着计算速度过慢的问题，而颗粒数量较少的道砟箱模型是一种兼顾计算精度与计算速度的模型，但道砟箱单轨枕试验及模拟的道砟受力状态与实际不符，其侧边颗粒运动被限制在竖直方向，且颗粒间咬合作用减弱。在实际道床中侧向边界上是相邻的道砟，底部边界是路基层，均为非刚性。但目前采用离散元道砟箱模型时少有学者考虑到边界条件对模拟结果的影响。因此，本文运用颗粒流软件PFC3D建立单轨枕-道砟箱离散元模型，使用真实道砟三维扫描模型建立真实形状刚性簇并按照规范粒径级配生成道砟。在此基础上，考虑侧向周期边界与竖向文克勒弹性路基边界，模拟分析了各边界条件及组合下道床的变形及受力状态，通过与刚性边界道砟箱模拟结果对比，探讨侧、竖向边界条件对道床沉降行为的影响。

1 离散元模拟与边界模型

1.1 单轨枕道砟箱及道砟模型

参照高速铁路设计规范[14]和道砟箱试验及数值模拟[9-11]，本文数值模型采用PFC3D建模。模拟区域的轨枕间距为600mm，轨枕尺寸为300mm长×250 mm宽×180 mm高，轨枕下方道砟层厚度为300mm。本文采用激光三维扫描真实道砟颗粒技术[5-6,15]，得到图1(a)所示的真实形状的道砟颗粒模型。综合考虑到计算效率与颗粒形状精确度，设定最大最小粒径比为0.8，平滑度为150，分别生成图1(b)所示的道砟颗粒簇。参考特级道砟规范[16]，道砟的粒径级配分布如图1(c)，中值粒径D50为40mm，不均匀系数Cu为1.56，密度为2550 kg/m3。参考前期数值研究[10]，道砟的法向和切向刚度均设为107N/m，道砟颗粒间摩擦因数为0.6，墙的刚度与摩擦因数与道砟一致。

图1 简化形状的道砟模型与级配Fig.1 Simplified shape of ballastmodelsand gradation

1.2 伺服运动墙单元模拟动荷载

道砟箱试验中采用正弦荷载加载，离散元模拟采用伺服控制实现循环加载，其原理为通过调整伺服墙的速度，并统计颗粒与墙的接触数，然后计算下一时步的伺服调整系数，随后开始下一阶段的伺服控制。通过控制墙的速度的大小方向变化，从而控制墙与颗粒的法向接触力接近目标应力。图2为采用刚性墙边界的单轨枕-道砟箱模型，通过伺服控制轨枕与下部道砟的法向接触力进行正弦循环加载，参考CHEN等[10-11]的数值模拟，本文采用峰值应力为533 kPa，最小应力为45 kPa，频率为15 Hz的正弦循环荷载进行加载，模拟列车时速约为150 km/h，对应的车辆轴重为16 t，转向架轴距为2.6m。

图2 刚性墙边界道砟箱模型Fig.2 Ballastbox testusingwallboundary

1.3 文克勒弹性路基边界

有砟道床的沉降主要发生在道砟层和底砟层，路基层沉降占比较小，但路基层存在弹性变形。文克勒(Winkler)路基模型的基本假定是路基上任一点的沉降仅与作用在该点上的压力成正比，而与相邻点处的压力无关，其中某点处的压力P(MPa)与沉降L(m)的比值K称为路基弹性模量。道砟箱试验中采用橡胶垫模拟路基层[4]，但是由于离散元方法的基本单元为刚性球、颗粒簇和刚性墙，以往模拟研究中大多数为刚性地基，不能有效地模拟地基的弹性变形。因此，本文提出一种平行黏结模型的九球颗粒组合结构，可实现弹性变形，如图3所示。在此可变形的弹性单元上施加荷载时，组合弹性单元压缩变形，在一定的压缩量内，施加的荷载与压缩量成正比，因此可用此种结构模拟文克勒弹性路基边界。首先对模型中的平行黏结接触参数进行标定，对上方的墙施加竖向速度5mm/s，并记录墙与结构的应力与位移，应力与竖向位移关系如图3所示，曲线斜率即为路基弹性模量，K=434.94MPa/m，对应于实际工况中的硬质路基。模拟中文克勒弹性结构接触参数为平行黏结法向和切向刚度为1010N/m，平行黏结抗拉强度和平行黏结黏聚力为8×1012Pa，摩擦因数为0.5。

图3 文克勒弹性单元应力-位移曲线Fig.3 Stress-displacementcurve ofWinkler elasticmodel

图4为采用文克勒弹性路基边界的单轨枕-道砟模型，在道砟层底部生成5块独立可上下运动的刚性板clump，并在其下放置5列×2行共10个独立的弹性单元。通过刚性板可将上部结构施加的力传递至底部弹性结构，记录5块独立刚性板的位置可以得出轨枕和轨枕间底部的路基不均匀变形规律。需要指出的是，刚性板之间间距为10mm，在模拟过程中不存在粒径较小的道砟嵌入路基层。

为验证本弹性单元的可行性，本文将模型底部划分为1-3共3种区域，分别记录在循环荷载加载过程中其沉降量的变化情况，如图4所示。图5为轨枕下部不同位置的路基沉降变形，可以看出该区域内沉降以弹性变形为主，塑性变形较小。随着加载进行，弹性变形量趋于稳定，约占累积沉降量的80%以上。由于轨枕正下方的应力更集中，区域1的沉降量显著高于两侧的区域2和3，也证实了这种弹性结构单元能有效模拟文克勒弹性路基。

图4 刚性墙&文克勒边界道砟箱模型示意图Fig.4 Ballastbox testusingWall&W inkler boundaries

图5 文克勒边界模型路基层各区域沉降量Fig.5 Settlementin each area of subgrade based on the Winklerboundarymodel

1.4 周期边界

图6为3个轨枕的道床示意图，其中左侧区间传递给中部区间的力P1应与中部区间传递给右侧区间的力P2相等，同样的，右侧区间传递给中部区间的力P3应与中部区间传递给左侧区间的力P4相等。在轨枕区间的交界处，存在着颗粒接触，这些颗粒可水平迁移，也可产生相互的咬合作用。以往模拟研究采用刚性墙边界，颗粒的水平位移受限，且无颗粒间咬合作用，边界区域的接触矢量只会为单一的水平矢量[10]。选取中部轨枕区间受力分析，左轨枕区间对其施加的力FL应与右轨枕区间对其施加的力FR大小相等，方向相反。因此，引入周期边界可研究侧向边界条件对道砟的影响。

图6 三轨枕道床受力示意图Fig.6 Force diagram of three sleepers track bed

PFC3D中的周期边界处颗粒质心在接触到边界后会出现在对侧。图7左右侧为周期边界。对球A施加水平向速度，当球B的质心通过边界时，球B会出现在对侧，并且在球B还未出现在对侧时，球B的实体已经占据了对侧空间，可以证明周期边界两侧存在力的传递，并且两侧颗粒在运动过程中的接触参数不会发生改变，在运动过程中的时间步长与非周期边界模型相同。图8为采用周期边界与文克勒弹性路基边界的单轨枕-道砟模型。边界处的道砟可以进行水平位移，模型左右两侧的颗粒可以接触并产生咬合作用，观察模型左右两侧的道砟可以发现，颗粒的质心位置决定了颗粒的左右侧分布。

图7 PFC中周期边界的颗粒运动Fig.7 Particlemovementat the periodic boundary in PFC

图8 周期&文克勒边界道砟箱模型示意图Fig.8 Ballastbox testusing Periodic&Winklerboundaries

2 不同边界条件下的模拟结果分析

2.1 不同边界条件下的轨枕沉降及动力特性

为分析各边界条件下轨枕沉降量的变化情况。参照试验加载，通过伺服控制墙运动模拟列车动荷载，并记录轨枕的永久变形量得到如下轨枕沉降对比图，如图9所示。通过对比刚性墙边界和刚性墙&文克勒边界，可以看出刚性墙&文克勒边界的轨枕沉降量略大于刚性墙边界的轨枕沉降量，且随着加载次数的增加，2种条件下轨枕沉降量差值不大，也验证了在硬质路基工况下，路基层沉降在轨枕总沉降中的占比较小。通过对比刚性墙边界和周期边界，可以看出周期边界的轨枕沉降量大于刚性墙边界的轨枕沉降量，且随着加载次数的增加，周期边界的轨枕沉降量增幅更大。

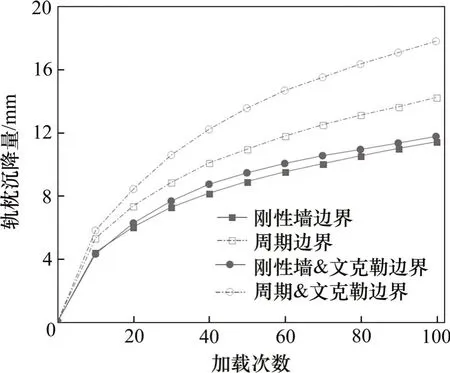
图9 不同边界条件下的轨枕沉降量Fig.9 Sleeper settlementunder differentboundary conditions

图10为第1，10，50和100次循环加载时刚性墙边界与周期边界下轨枕应力-沉降曲线。随着加载次数的增加，滞回环内区域由宽变窄，这是由于道砟在加载初始阶段较为松散，随着加载次数的增加，道砟受到挤压而变得更为密实，弹性变形及塑性变形减小。与周期边界的结果对比，也可看出滞回曲线形态特征类似，但同一加载时刻，周期边界下轨枕沉降量更大。综合考虑轨枕沉降量与弹性变形量，可以得出在周期&文克勒边界双重作用下道砟弹性模量最小，刚性墙边界下的道砟弹性模量最大。该结果也间接表明单轨枕道砟箱试验中刚性边界条件对道砟弹性变形的影响，与实际道砟层受力存在一定差异。

图10 循环荷载作用下道砟箱的应力-沉降曲线Fig.10 Stress-settlementcurvesof box testsimulation under cyclic loading

2.2 各边界条件下侧向接触力对比

本文通过提取模型在第50个加载峰值时侧边宽为10mm区域的接触力信息，得出了不同边界条件下各模型的侧向接触力的分布玫瑰云图，如图11所示，长度代表对应角度区间内的颗粒平均法向接触力大小。由图可知，由于刚性墙侧边界的接触为颗粒-墙接触，侧向接触力多为水平方向；相比而言，周期侧边界的道砟箱，侧边接触为颗粒-颗粒接触，接触力的分布范围会变广；通过比较侧向接触力的数量及平均值，可以看出周期边界下侧向平均接触力相较于刚性墙边界减少了50.2%，周期&文克勒边界下侧向平均接触力相较于刚性墙&文克勒边界减少了43.4%。因此，相较于刚性墙边界，周期边界的侧边接触力不会只有水平向，并且由于没有刚性墙边界的位移限制，周期边界的侧向接触力会下降。

图11 4种边界条件下的侧向接触力分布Fig.11 Lateralcontact force distribution nephogram under fourboundary conditions

为了分析各边界条件下不同深度的侧向接触力差异，以轨枕底面位置为分界线，划分6个50mm的深度区间。第50个循环荷载峰值时，按深度区间统计接触力得到侧向接触力-深度区间柱状图，如图12所示。总体而言，在深度区间为0～150mm时，侧向接触力会随着深度增大而增加，在深度区间为150～200mm时，侧向接触力会减小，侧向接触力峰值出现在200～250mm区间。模型接触力链分布如图13所示，道砟间应力链集中于轨枕下方，且在刚性墙边界时扩散传递更为明显。

图12 4种边界条件下道砟的侧向接触力分布Fig.12 Lateral contact force distribution of themodelunder fourboundary conditions

图13 第50次加载峰值时的内部接触力链分布Fig.13 Distribution of the contact force chain at the 50th loading peak

通过对比刚性墙边界与周期边界处的侧向接触力，可以发现周期边界的平均侧向接触力比刚性墙边界减少了41%，峰值侧向接触力减少了45%，这是因为刚性墙边界对颗粒的约束能力超过周期边界，在边界处的颗粒受到挤压但无法水平位移，因此会产生更大的侧向接触力，但在实际道床中并不存在刚性边界，故使用周期边界模拟单轨枕-道砟模型更接近实际情况。

通过对比刚性墙边界与刚性墙&文克勒边界处的侧向接触力，可以发现刚性墙&文克勒边界的平均侧向接触力比刚性墙边界增加了19%，这是由于在道砟底部引入了弹性文克勒单元，其刚性有所减小，故分担到底面的力减小，分担到侧边的力增加。在实际道床中，其底部不是刚性墙，使用文克勒弹性路基结构更能反映出路基的弹性特性。周期&文克勒边界条件的模型同时具备了2种边界特性，既考虑了模型两侧颗粒的水平运动，也考虑了模型底部的弹性特性，因此该模型与道砟层的真实受力状态更为接近。

2.3 周期边界下的颗粒运动情况和细观分析

为了从宏观上阐明周期边界下模型中颗粒的位移变化，图14为刚性墙边界与周期边界下侧边颗粒的位移分布图。由图可见，刚性墙边界下的颗粒位移方向主要集中于竖向，并且在中间区域可看出有一段位移空腔，这说明了颗粒受到刚性墙边界的约束从而较难发生位移；周期边界下的颗粒位移的方向则不集中于竖向，而是呈现向右侧的放射状方向，并且各个深度段的颗粒均会发生位移，这说明了周期边界降低了颗粒在侧边的约束，使其可以进行各方向上的位移。

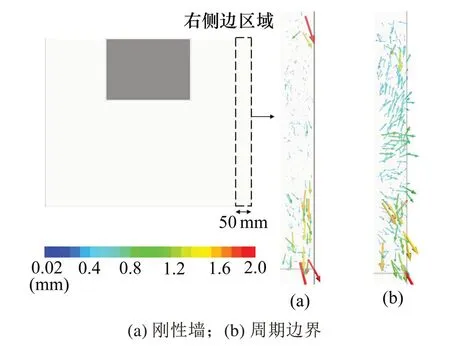
图14 侧边区域颗粒位移矢量分布图Fig.14 Lateraldisplacementvectorsof particles in side area

侧边界的局部孔隙率能反映不同边界条件下模型中颗粒的密实程度。由于刚性簇颗粒的重合导致测量圆中的孔隙率存在一定误差，本文采用M atlab自编程序测量非球形颗粒簇的孔隙率，图15(a)中虚线包围部分即为局部孔隙率测量区域。对比局部孔隙率的变化，可以看出刚性墙边界下的局部孔隙率大于周期边界的局部孔隙率，且随着加载次数的增加，局部孔隙率都有下降的趋势。这反映了周期边界下的颗粒相较于刚性墙边界更加密实，随着加载次数的增加，局部孔隙率的减小趋势放缓，最后趋于稳定。在循环加载过程中颗粒间的相互挤压而产生配位数的变化，因此颗粒间的平均接触数可以一定程度反应加载过程中颗粒的运动特性。图15(b)为刚性墙边界与周期边界下模型中测量圆内平均接触数的变化情况，可以发现随着加载的进行，颗粒间的平均接触数增大，表明颗粒逐渐密实，且在周期边界下的平均接触数大于刚性墙边界，这也表明周期边界下颗粒的密实程度更高。

图15 刚性墙边界与周期边界的孔隙率及平均接触数变化Fig.15 Comparison of porosity and coordination numberusingwallboundary and periodic boundary

3 结论

1)采用PFC3D平行黏结模型建立九球颗粒组合结构，并通过压载标定试验获取了平行黏结键的细观参数，可有效模拟地基的弹性变形，以此建立离散元“轨枕-道砟-路基”整体模型。

2)在模型中引入不同边界条件讨论其对道床沉降的影响，结果表明不同边界条件下模型对颗粒的约束能力存在差异。相较于刚性墙边界，周期边界与文克勒弹性路基边界下的轨枕沉降量增大、模型弹性模量减小，其中周期边界下的侧向接触力矢量分布范围增加，侧向接触力减少了41%，文克勒边界下的侧向接触力矢量分布范围变化不明显，侧向接触力增加了19%。2种边界条件的引入使得边界颗粒更接近真实受力状态。

3)引入周期边界的模型中侧边区域颗粒的位移大于刚性墙边界模型，且运动方向更分散，局部孔隙率减小，平均接触数增大，表明在荷载作用下，侧向周期边界处道砟颗粒存在咬合作用且运动方向不受限。

后期研究可通过设置周期边界条件将有砟轨道划分为4根轨枕的轨道段(约为转向架轴距)为一个计算单元，可进行大尺寸的有砟轨道离散元模型，且边界处道砟的受力状态更接近真实。