基于均值偏差奖赏函数的放煤口控制策略研究

罗开成，高 阳，杨 艺，3，常亚军，袁瑞甫

(1.郑州煤矿机械集团股份有限公司，河南 郑州 450016；2.郑州煤机液压电控有限公司，河南 郑州 450016；3.河南理工大学 电气工程与自动化学院，河南 焦作 454000；4.煤炭安全生产与清洁高效利用省部共建协同创新中心，河南 焦作 454000)

综合机械化放顶煤开采(简称综放开采)的智能化建设是推进我国煤炭行业改造升级的重要环节[1，2]。智能感知、智能决策和自动控制是智能化开采的三要素[3]。在智能化开采中，利用智能感知系统实时监测顶煤量、煤流量等工作面状态信息，智能化放煤决策系统根据监测到的信息进行决策，建立“智能感知-决策”机制是综放开采智能放煤工艺的发展方向[4，5]。文献[6]利用雷达探测技术、激光三维扫描技术以及煤矸识别等技术，实现了对开采顶煤厚度、放煤空间剩余顶煤量以及放出煤流中煤矸比例的实时监测，工作面自动化系统根据实时监测数据对放煤口动作进行决策，控制放煤口动作。该方法在工业性实验中取得了不错的效果，初步实现了智能化放煤。目前，智能决策发展相对滞后[7]。如何根据综放工作面放煤环境状态信息对支架放煤口的动作进行决策，实现放煤口动作随放煤环境的变化而自动调整，是放煤工艺智能化的关键。因此，本文所在课题组根据马尔可夫决策过程基本原理，将放顶煤过程抽象为马尔可夫决策过程，建立了基于强化学习的放顶煤智能决策模型，控制放煤口动作，为建立放煤口智能决策机制提供思路[8-10]。

本文针对以往建立的基于Q-learning放顶煤智能决策模型不能从综放工作面全局角度出发学习支架放煤口控制策略，导致在放煤过程中存在放煤口间动作配合简单，协同性差的问题，从工作面全局角度出发学习放煤口控制策略，并将控制煤岩分界面形态也作为智能体学习的目标，建立了基于均值偏差奖赏函数Q-learning放顶煤智能决策模型，提升综放工作面放煤过程中放煤口间动作的配合度和协同性，使其能够更好地控制放煤过程，提升工作面放煤效果。

1 放顶煤智能决策模型

1.1 放煤过程的马尔可夫决策过程

强化学习的基础是马尔可夫决策过程(Markov Decision Process，MDP)。MDP是一种用于对环境建模的模型，大部分强化学习问题都可以建立MDP模型，从而在理论方面为强化学习奠定了良好的框架[11]。马尔可夫性是指环境下一个状态st+1只与当前状态st有关，而与以往的历史状态无关。设P为状态之间的转移概率，马尔科夫性的数学描述为：

P[st+1|st]=P[st+1|st，…，s1]

(1)

MDP可以用五元组M={S，A，R，P，γ}表示，状态空间为S={s1，s2，…，sn}，其中si表示智能体所处的环境状态，i=1，2，…V，n，n表示状态空间的维度；动作空间为A={a1，a2，…，am}，其中aj为智能体可以选取的动作，j=1，2，…，m，m表示动作空间的维度；R表示状态转移后得到的奖赏值；P表示环境状态转移概率；γ为折扣因子，表示未来奖励对当前决策的影响程度。

在放顶煤过程中，支架放煤口的控制过程是一个时间序列，其决策依赖于工作面当前的放煤状态信息及上一次放煤的结果，具备马尔科夫性。因此，控制放煤口的决策过程是典型的马尔可夫决策过程，并可以用强化学习解决[8]。

1.2 Q-learning算法原理

由于综放开采中环境状态转移概率P是未知的，导致无法建立决策过程完备的放顶煤MDP模型，从而导致无法利用基于动态规划的方法求解MDP决策问题。但在强化学习Q-learning算法中，智能体不需要知道环境状态转移概率P，只需要确定状态空间S、动作空间A以及奖赏函数R，智能体即可学习环境最优策略，这与本文研究的需求高度契合。因此，本文选取Q-learning算法来解决放顶煤MDP决策问题，获取支架放煤口最优控制策略。

在Q-learning算法中，通过优化一个可迭代计算的动作值函数Qπ(s，a)来获取最优策略[12]。动作值函数Qπ(s，a)是指根据当前策略π，从状态s出发选择动作a后能够获得累积奖赏的期望值，其定义如下：

(2)

智能体基于贝尔曼最优性原理更新动作值函数Qπ(s，a)，使其趋近最优策略的动作值函数，更新方式如下：

Qπ(s，a)←Qπ(s，a)+α[R(s，a)+

(3)

式中，s为当前时刻状态；a为状态s下选择的动作；s′为执行动作a后的新状态；a′为在状态s′下能使其动作值函数最大的动作；π为当前策略；α∈(0，1)表示学习率；γ∈(0，1)为折扣系数。

当状态空间中所有状态对应的动作值函数都收敛后，此时的策略即为最优策略。

在Q-learning算法中，智能体每次贪婪地选择当前状态对应动作值函数最大的动作。这种利用当前知识使得立即奖赏值最大的方法，实际上可能忽略了能带来更大奖励的动作。为增加Q-learning“利用”已有知识和“探索”新知识的性能，本文采用ε-greedy算法作为选择动作的策略，其表达式为：

(4)

式中，ε∈(0，1)，表示探索率；|A(s)|是状态s条件下可选动作的数量；a*为最大动作值函数对应的动作。

1.3 放顶煤MDP建模

在之前建立的Q-learning放顶煤智能决策模型中，定义的MDP参数存在以下不足：①仅根据顶煤含量确定顶煤赋存状态，标准过于单一；②仅根据放出体状态定义奖赏函数R，奖赏函数与放煤目标之间的关联关系不够高，导致智能体学习到的放煤口控制策略无法使工作面放煤效果达到最佳；③动作空间A中仅有打开和关闭两个动作，智能体可选择的动作较少。针对以上不足，本文重新定义了状态空间S、动作空间A以及设计了一种新的奖赏函数R，优化放顶煤智能决策模型，提升工作面放煤效果。

1.3.1 状态空间S设计

1)顶煤赋存状态特征。将支架放煤口上方以及掩护梁后方作为检测区域，检测区域内的顶煤含量作为顶煤赋存状态的特征之一，记为w。其中，第i台支架检测区域内顶煤含量计算如下：

(5)

式中，mi为第i台支架检测区域内的顶煤量；ni为第i台支架检测区域内的矸石量。wi越大，则说明当前支架检测区域内待放顶煤越充足。

结合第i台支架检测区域内的顶煤含量wi与所有支架检测区域内顶煤含量的平均值waverage，定义了第i台支架的均值偏差量特征μi：

μi=wi-waverage

(6)

式中，wi为第i台支架对应检测区域的顶煤含量；waverage为所有支架对应检测区域顶煤含量的平均值；N为综放工作面上液压支架的数量。当μi>0时，代表第i台液压支架检测区域顶煤含量高于所有支架顶煤含量的平均水平。

2)顶煤赋存状态。根据顶煤含量w与均值偏差量μ共同确定支架放煤口上方顶煤赋存状态。但由于Q-learning在处理连续状态时容易出现维度爆炸的问题[13]。因此，考虑到算法的收敛速度，还需要对顶煤含量w与均值偏差量μ进行离散化处理。根据顶煤含量w与均值偏差量μ的不同离散等级的组合，可以定义不同的顶煤赋存状态sn，其定义为：

sn=(wl，uj)

(7)

式中，wl=[w1，w2，…，wl]为顶煤含量w的离散等级空间，l代表其维度大小；uj=[u1，u2，…，uj]为均值偏差量μ的离散等级空间，j代表其维度大小。

对应的状态空间S为：

S={s0，s1，…，sn}

(8)

式中，n为状态空间的维度。

1.3.2 动作空间A设计

在综放开采中，可以通过调节放煤口的开口度调节放煤量[14]。因此，根据放煤口开口度大小定义放煤口动作，对应的动作空间A为：

A={a1，a2，a3，a4}

(9)

式中，a1代表关闭放煤口；a2代表放煤口全开；a3代表放煤口半开；a4代表放煤口打开三分之二开口度。

1.3.3 均值偏差奖赏函数R设计

本文结合放出煤流状态与顶煤赋存状态特征两个方面定义了均值偏差奖赏函数R：

R=Rcoal+Rdev

(10)

式中，Rcoal是与放出煤流状态相关的奖赏函数；Rdev是与均值偏差特征μ相关的奖赏函数。

1)Rcoal奖赏函数。在综放开采中，现场工人一般根据放出煤流中的煤矸比例控制放煤口的开闭。因此，定义奖赏函数Rcoal：

Rcoal=λ1M1+λ2M2

(11)

式中，λ1代表放出单个顶煤的奖励，M1代表放煤口动作后放出顶煤的数量，λ2代表放出单个矸石的奖励，M2代表放煤口动作后放出矸石的数量。

2)Rdev奖赏函数。通过对放顶煤过程分析可以得到，当煤岩分界面均匀下降时，各支架检测区域内顶煤赋存状态的均值偏差量特征μ在数值上相互接近。因此，根据均值偏差量特征μ的离散等级设计奖赏函数，记为Rdev，见表1。

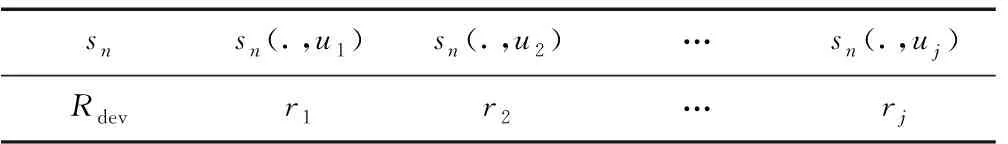
表1 奖赏函数Rdev

在奖赏函数Rdev中，当放煤口执行动作后，放煤口上方顶煤赋存状态的均值偏差量μ越接近0，则获得的惩罚rj越小，反之获得的惩罚rj越大，从而引导智能体学习保持煤岩分界面均匀下降。

在放顶煤过程中，当煤岩分界面即将达放煤口或者已经到达放煤口时，智能体的注意力集中在矸石的放出。如果此时继续学习保持煤岩分界面均匀下降，智能体将忽略部分矸石的放出，从而导致放煤效果下降。因此，需要对奖赏函数Rdev的使用进行约束。约束后的奖赏函数R为：

R=Rcoal+C×Rdev

(12)

(13)

当sn(wl，.)<0.3，代表当支架放煤口上方的顶煤含量小于30%，此时智能体将不再学习保持控制煤岩分界面形态，而专注于控制矸石的放出。

1.4 Q-learning算法框架

当状态空间S、动作空间A以及均值偏差奖赏函数R确定后，利用Q-learning算法在线学习顶煤赋存状态与支架放煤口动作之间的最优映射关系，获取支架放煤口最优控制策略。智能体的学习过程可以描述为：在与环境交互的过程中，智能体不断获取顶煤赋存状态sn，支架放煤口动作a以及环境反馈的奖赏值R等知识。智能体根据获取到的知识，按照式(3)计算并更新对应放煤口动作的动作值函数Qπ(s，a)，直到所有的动作值函数都收敛到最优。在选择放煤口动作时，智能体根据已经学习到的当前顶煤赋存状态下放煤口动作的动作值函数Qπ(s，a)，按照式(4)选择当前放煤口的动作与放顶煤环境进行交互。Q-learning算法框架如图1所示。

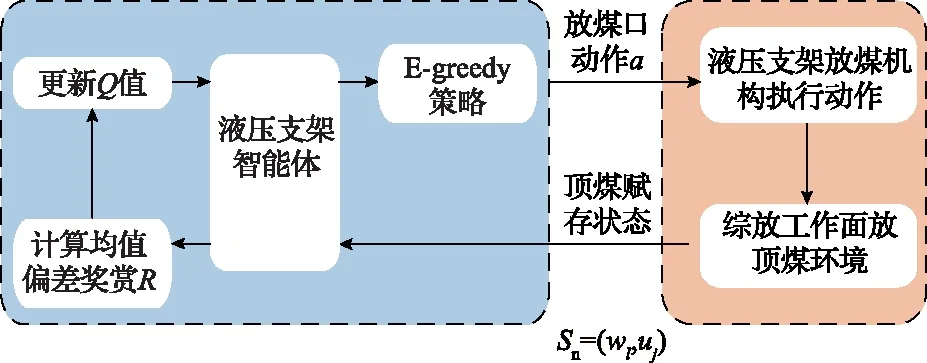
图1 Q-learning算法框架

2 放煤口控制模型三维仿真实验及结果分析

2.1 综放工作面进刀放煤三维仿真平台

本文结合YADE开源代码，在Ubuntu系统上开发了一种基于离散元方法的综放工作面进刀放煤三维仿真实验平台，对放顶煤智能决策模型展开研究，如图2所示。在仿真模型中绿色颗粒代表顶煤，红色颗粒代表矸石。当顶煤通过放煤口被放出时，顶煤颜色由绿色变为蓝色，与未放出的顶煤做区别。图2中，黄色边框标识的区域为支架顶煤赋存状态的检测区域。当训练本文放顶煤智能决策模型时，仿真模型会在每一个训练步读取检测区域内的顶煤颗粒与矸石颗粒的数量，然后根据式(5)和式(6)分别计算顶煤含量w和均值偏差量μ的大小，并将计算结果传递给智能体确定当前顶煤赋存状态。在仿真模型中共设置了4个放煤口动作，与前文1.3小节定义的动作空间式(9)对应起来，4个放煤口动作的效果如图2所示。当本次放煤工序结束后，从工作面首台支架开始，逐架移动支架，从而实现工作面连续进刀放煤，移架过程如图3所示。在仿真模型中放煤高度3.8m，采高3.8m，采放比为1∶1，连续放3刀顶煤。

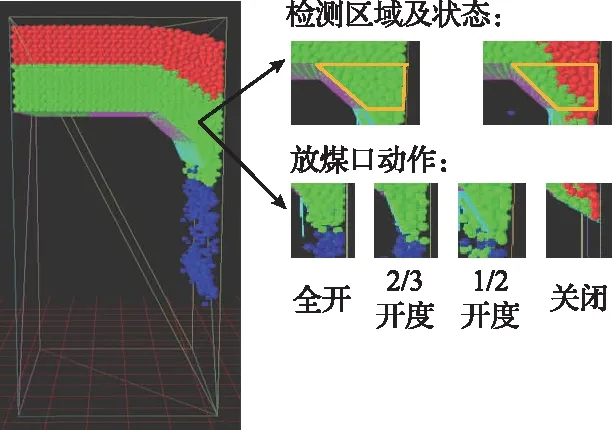
图2 进刀放煤三维仿真

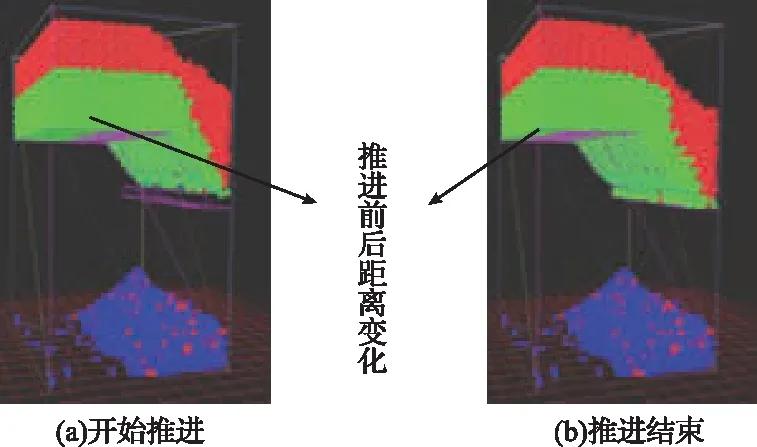
图3 综放工作面推进过程

模型中煤与矸石颗粒材料参数根据塔山矿8222综放工作面设计，其主要参数见表2。

表2 煤与矸石颗粒的主要力学参数

放煤口控制模型中共设置了10台液压支架，液压支架根据塔山矿8222综放工作面中实际液压支架设计，其主要参数：液压支架宽度为1.5m，液压支架高度为3m，掩护梁长度为3.8m，尾梁长度为2m，顶梁与掩护梁之间的夹角为50°，尾梁上摆与掩护梁的夹角为15°，尾梁下摆与掩护梁的夹角为45°。

2.2 模型参数设置

基于均值偏差奖赏函数放顶煤智能决策模型核心Q-learning算法的参数设置为：α=0.1，γ=0.9，ε=0.5。

2.2.1 状态空间参数设置

根据现场工人的经验与前期实验的结果，确定式(7)中wl的离散等级空间维度l=5，uj的离散等级空间维度j=7，结果见表3、表4。

表3 状态特征w离散区间划分

表4 状态特征μ离散区间划分

根据顶煤含量wl与均值偏差量uj不同离散等级的组合，共定义了17种顶煤赋存状态，见表5。

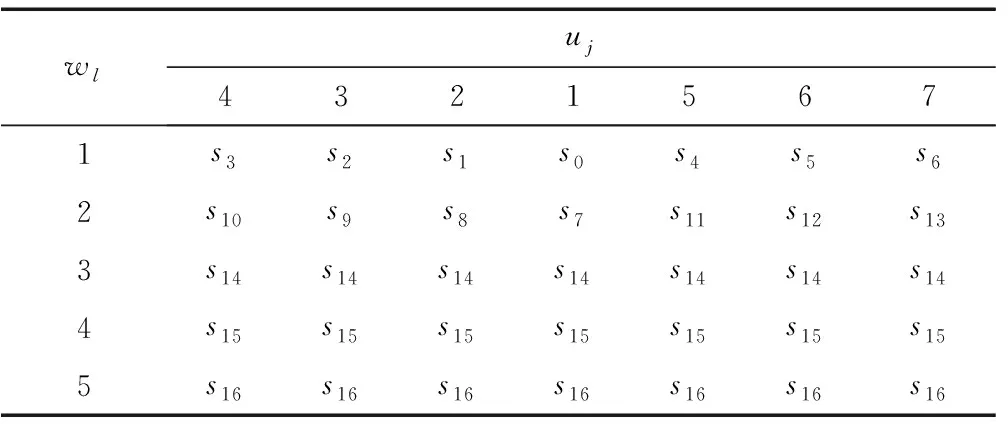
表5 状态空间

在训练过程中，当仿真模型将顶煤含量w和均值偏差量μ的计算结果传递给智能体后，智能体将根据表3和表4分别确定两者所处的离散等级，最后智能体再根据表5确定当前支架检测区域内的顶煤赋存状态。

2.2.2 均值偏差奖赏函数参数设置及计算

设置Rcoal的参数为：λ1=3，λ2=-7；Rdev的参数为：r1=-20，r2=-30，r3=-70，r4=-200，r5=-10，r6=-20，r7=-50。在训练过程中，一方面，仿真模型会检测支架放煤口动作后放出的顶煤颗粒和矸石颗粒的数量，并将检测结果传递给智能体，智能体根据式(11)计算获得奖赏Rcoal的大小。另一方面，受放煤口动作的影响，顶煤赋存状态发生变化，智能体根据表1确定获得奖赏Rdev的大小。当Rcoal和Rdev的奖赏确定后，再根据式(12)和式(13)计算此次放煤口动作，智能体最终获得的奖赏。

2.3 训练流程

当参数确定后，对放顶煤智能决策模型进行训练，训练流程如图4所示。

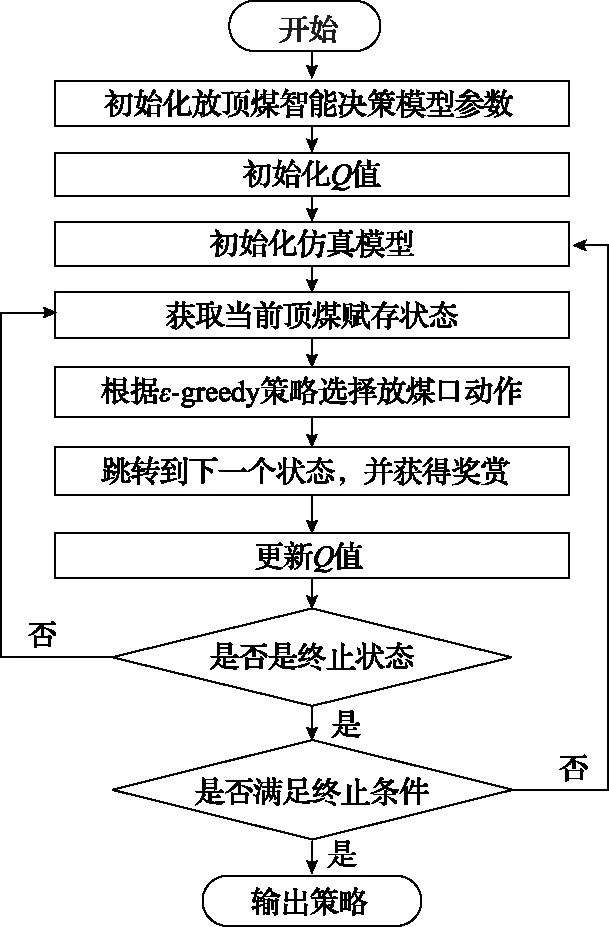
图4 训练流程图

2.4 仿真测试过程和结果分析

本文基于进刀放煤三维仿真实验平台，对建立的放顶煤智能决策模型、原Q-learning智能放煤工艺以及单轮顺序放煤工艺，在连续放3刀煤条件下的放煤效果进行测试。其中，单轮顺序放煤工艺按照“见矸关窗”的原则，当仿真模型检测到放煤口瞬时放出煤流中矸石比例超过30%时关闭放煤口[15]。

在仿真测试过程中，由于第二刀与第三刀放煤过程中的煤矸运动过程和煤岩分界面形态不易观察。因此，在这里仅展示了各放煤工艺第一刀详细放煤过程，如图5所示。

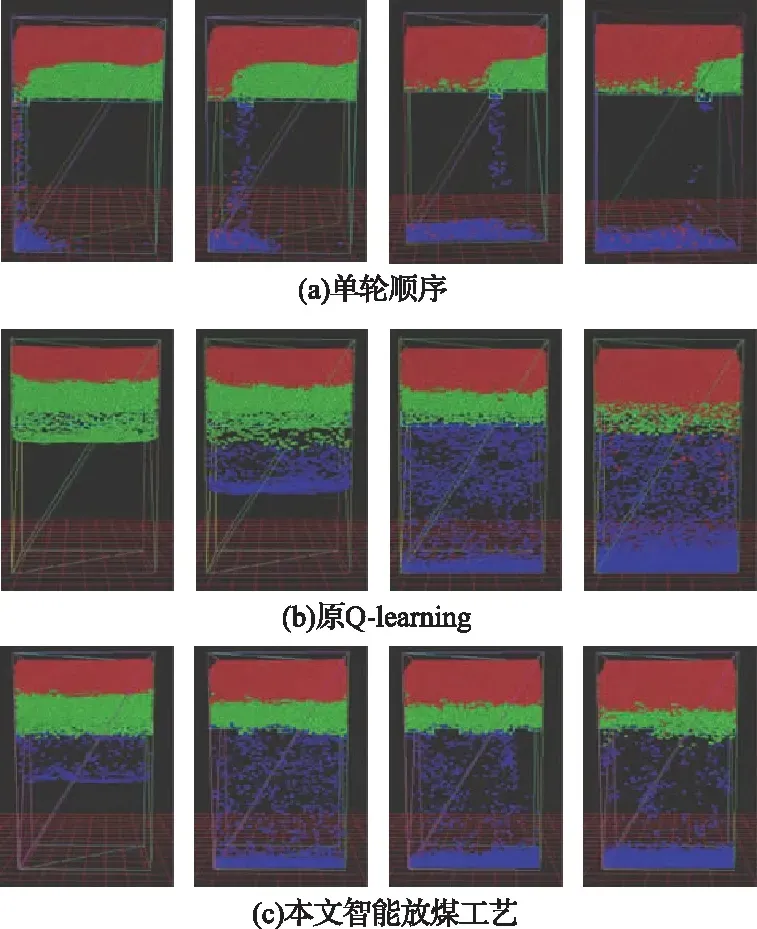
图5 三种放煤工艺的放顶煤过程

单轮顺序放煤过程如图5(a)所示。由于每次只打开一个放煤口放煤，导致单个支架放煤口的放煤量巨大，煤岩分界面迅速下降，几乎与放煤口垂直。当相邻放煤口放煤时，窜矸现象严重，可能导致放煤口提前关闭，从而降低顶煤采出率。并且由于每次只打开一个放煤口放顶煤，也将导致综放工作面放煤时间过长，放煤效率低。此外，在单轮顺序放顶煤过程中支架放煤口上方可能会发生顶煤成拱堵塞放煤口的现象，导致顶煤无法顺利放出，降低顶煤采出率，如图6所示。

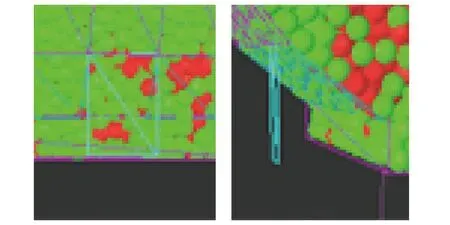
图6 顶煤成拱现象

原Q-learning智能放煤工艺的放顶煤过程，如图5(b)所示。与单轮顺序放煤工艺相比，煤岩分界面比较均匀地下降，放煤效率高。在原Q-learning智能放煤工艺中，支架放煤口动作虽然可以随顶煤赋存状态的变化而实时调整。但仔细观察各支架放煤口动作可知，放煤口间动作配合简单。当顶煤含量高时，控制放煤口打开；当顶煤含量低到一定程度时，控制放煤口关闭。由此可见，其支架放煤口控制策略比较简单。并且由于综放工作面上不同位置的液压支架打开放煤口放煤时，放煤口上方煤矸运移的速率是不相等的。因此，原始Q-learning算法学习到的控制策略是不可能很好地保持煤岩分界面平整度，从而无法使综放工作面放煤效果达到更高水平。

智能放煤工艺放顶煤过程如图5(c)所示。观察其放顶煤过程可以发现，与原Q-learning智能放煤工艺放顶煤过程相比，本文智能放煤工艺在放顶煤过程中煤岩分界面下降更加均匀，分界面平整度保持更好。根据放顶煤理论可知，在放顶煤过程中保持煤岩分界面均匀下降有利于提高顶煤采出率。与原Q-learning智能放煤工艺不同，在本文智能放煤工艺放顶煤过程中，各支架放煤口间动作高度协调，协同性好。

由上述分析可知，基于均值偏差奖赏函数放顶煤智能决策模型，可以使智能体在与环境交互的过程中学习到更加优秀的放煤口控制策略。智能体根据学习到的放煤口策略，更好地控制了放顶煤过程。

在仿真平台上各放煤工艺连续3刀放煤的结果见表6。由表6可知，与另外2种放煤工艺相比，该智能放煤工艺放出顶煤的平均数量为5292.5，相对于单轮顺序放煤的4752.5与基于Q-learning智能放煤工艺的5067.3，分别提高11.4%以及4.44%。放出矸石的平均数量为344.6，低于基于Q-learning智能放煤工艺的403.5，但高于单轮顺序放煤工艺的288.3。从放出煤与矸石带来的总奖赏看，该智能放煤工艺放出煤与矸石带来的平均奖励为13467.8，比单轮顺序放煤工艺提高约10%，比基于Q-learning智能放煤工艺提高约8.8%。由此可见，智能放煤工艺可以有效提升综放工作面放煤效果。此外，本文对6次实验放出顶煤数量、矸石数量以及放煤总奖赏求方差，结果见表7。

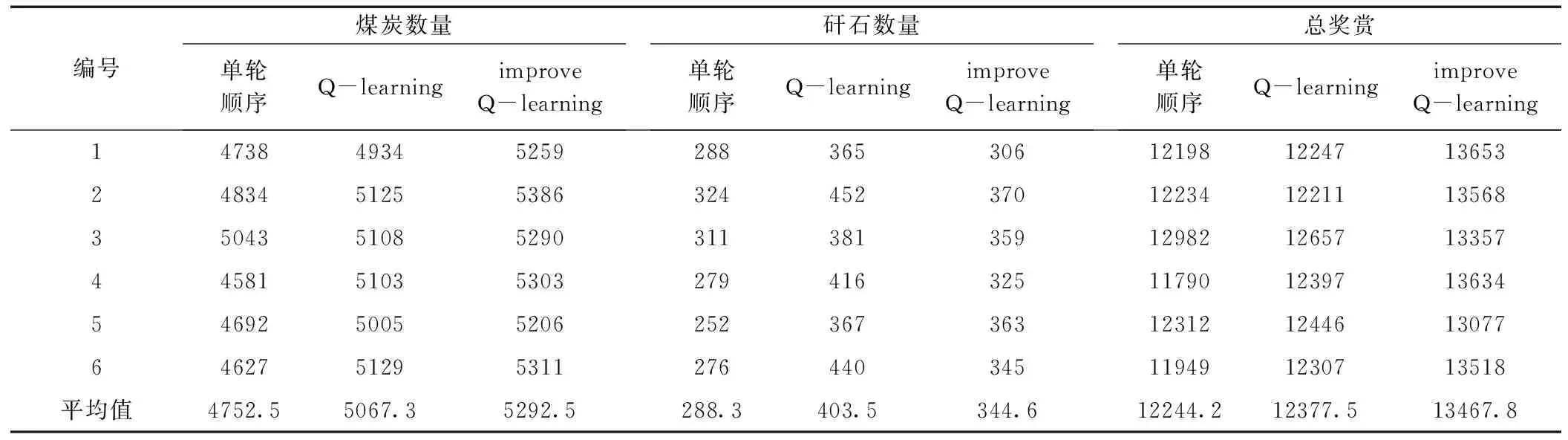
表6 连续进刀放煤实验结果

由表7可知，智能放煤工艺6次实验中，在放出顶煤数量、矸石数量以及放煤总奖赏三个方面数据的方差均小于其它两种放煤工艺，说明了智能放煤工艺与其它两种放煤工艺相比，放煤效果更加稳定。

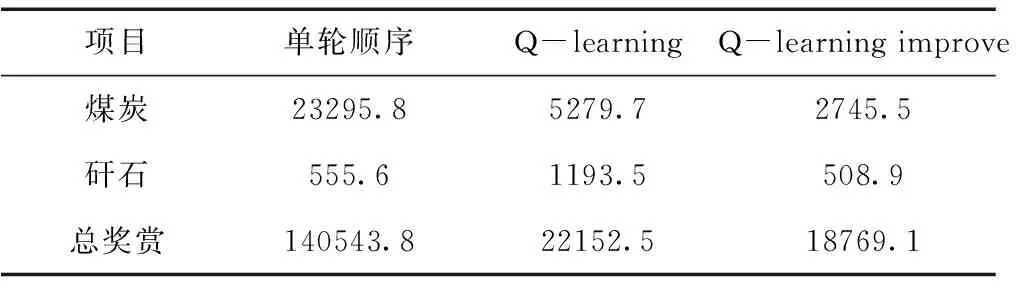
表7 放出顶煤、矸石数量以及总奖赏的方差

3 结 论

1)提出了一种基于均值偏差奖赏函数放顶煤智能决策模型。该模型根据当前支架放煤口上方顶煤的赋存状态对放煤口动作进行决策，实现放煤口动作随待放顶煤赋存状态的改变而实时调整。并且在三维仿真实验平台上的仿真过程表明，智能体基于均值偏差奖赏函数学习到的放煤口控制策略，可以使各液压支架在放顶煤过程中放煤口动作配合更加紧密，从而保持煤岩分界面均匀下降，分界面平整度达到较为理想状态。

2)在三维仿真实验平台上的实验结果表明，智能放煤工艺在工作面连续进刀放煤条件下，放煤平均奖励13467.8，比基于Q-learning智能放煤工艺提高8.8%，比单轮顺序放煤工艺提高约10%。因此，本文提出的智能放煤工艺可以有效提升综放工作面的放煤效果。

3)由于Q-learning算法不易处理连续环境状态，因此本文将放煤口环境状态进行离散化处理。但环境状态的离散化会使得放煤口的控制精度降低。因此，在后续研究中，课题组将进一步研究放煤口环境状态的连续表达方式以及强化学习的最优决策模型，以提升放煤口的控制精度，从而进一步提升放煤效果。