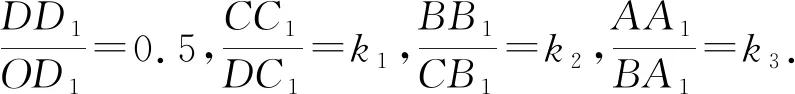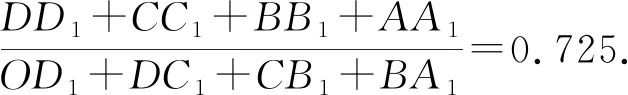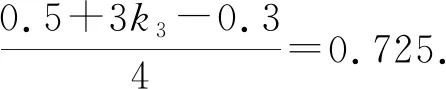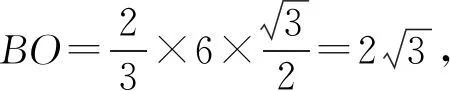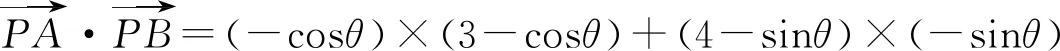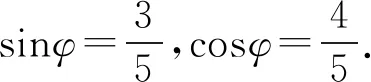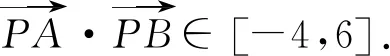数学建模视角下对2022年高考卷剖析
2022-09-22潘冬丽
潘冬丽
(广东省肇庆市第一中学 526020)
数学建模作为核心素养的一项关键部分,在处理分析实际问题时往往可以做到事半功倍.如果能把问题进行模型化,数据就可以可视化,图形就可以立体化.本文以2022年高考题为例剖析数学建模本质,进而有效培养学生的建模思维.
1 建立模型构造
高中数学建模构建的核心就是几何与代数有机融合.突破数学代数结构特征与几何知识相关,能够从数学问题挖掘、构建几何模型去解决.
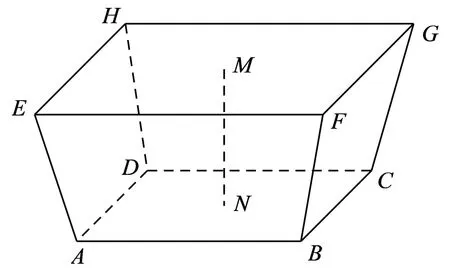
图1
A.1.0×109m3B. 1.2×109m3
C. 1.4×109m3D. 1.6×109m3
解析依题意可知棱台的高为MN=157.5-148.5=9(m),所以增加的水量即为棱台的体积V.
棱台上底面积S=140.0km2=140×106m2,下底面积S′=180.0km2=180×106m2,

≈(96+18×2.65)×107
=1.437×109
≈1.4×109(m3).
例2(2022年全国高考甲卷理科第7题)在长方体ABCD-A1B1C1D1中,已知B1D与平面ABCD和平面AA1B1B所成的角均为30°,则( ).
A.AB=2AD
B.AB与平面AB1C1D所成的角为30°
C.AC=CB1
D.B1D与平面BB1C1C所成的角为45°
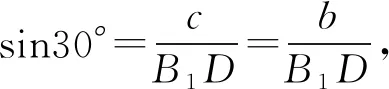
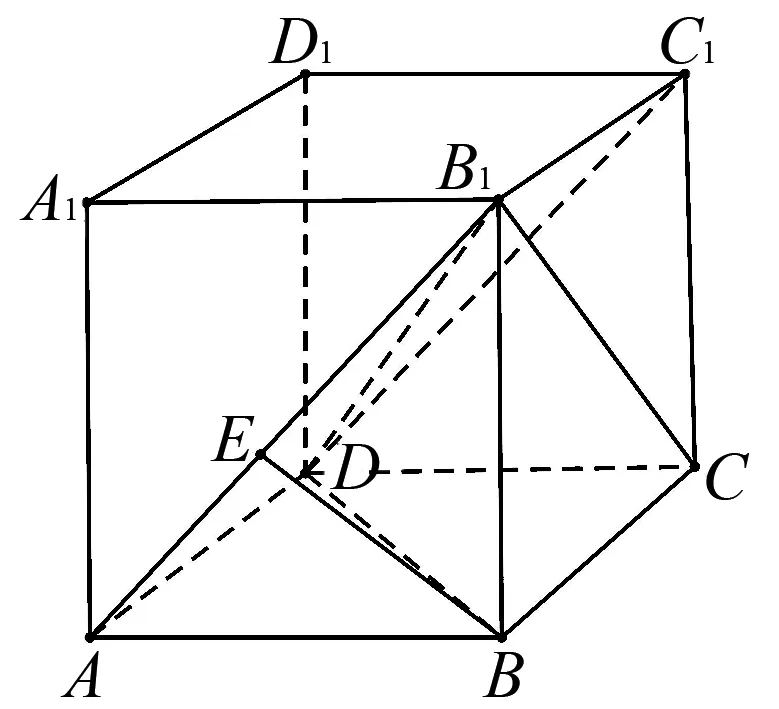
图2
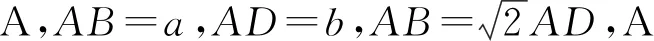
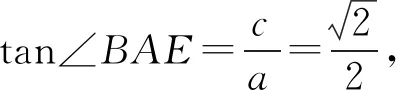
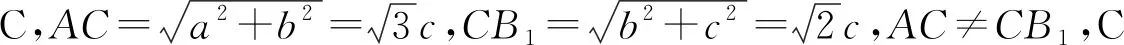
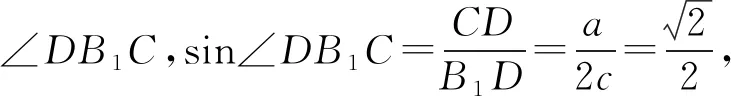
故选D.
例3 (2022年新高考Ⅰ卷第14题)写出与圆x2+y2=1和(x-3)2+(y-4)2=16都相切的一条直线的方程____.
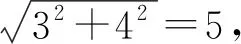

图3


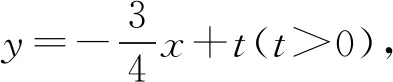
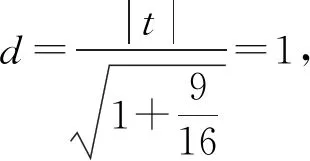
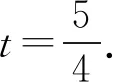

当切线为m时,设直线方程为kx+y+p=0,其中p>0,k<0,
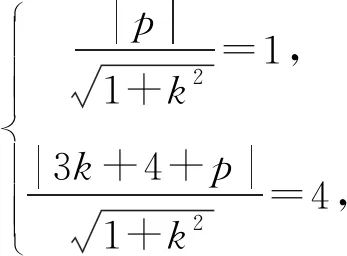


当切线为n时,易知切线方程为x=-1,

2 突破建模情景
常规问题很难解决时,我们通过构建数学模型,调整思维角度,敢于构想新的问题意境,往往柳暗花明又一村.
例4 (2022年新高考Ⅱ卷第12题)若x,y满足x2+y2-xy=1,则( ).
A.x+y≤1 B.x+y≥-2
C.x2+y2≤2 D.x2+y2≥1

由x2+y2-xy=1可变形为
解得-2≤x+y≤2.
当且仅当x=y=-1时,x+y=-2,当且仅当x=y=1时,x+y=2,所以A错误,B正确;
由x2+y2-xy=1可变形为
解得x2+y2≤2.
当且仅当x=y=±1时取等号,所以C正确;
因为x2+y2-xy=1变形可得
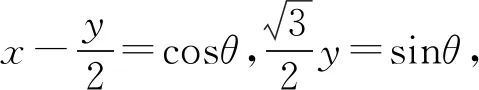
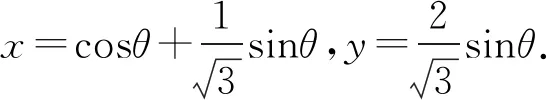

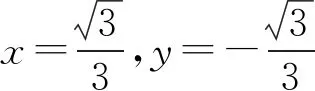
但是x2+y2≥1不成立,所以D错误.
故选BC.

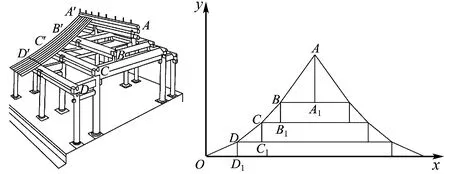
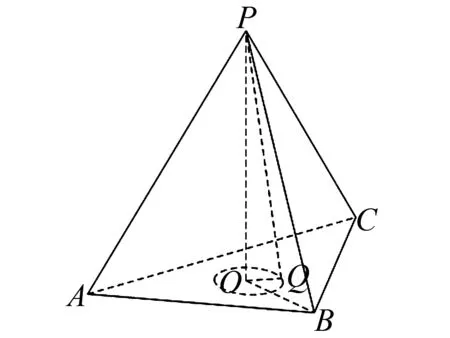
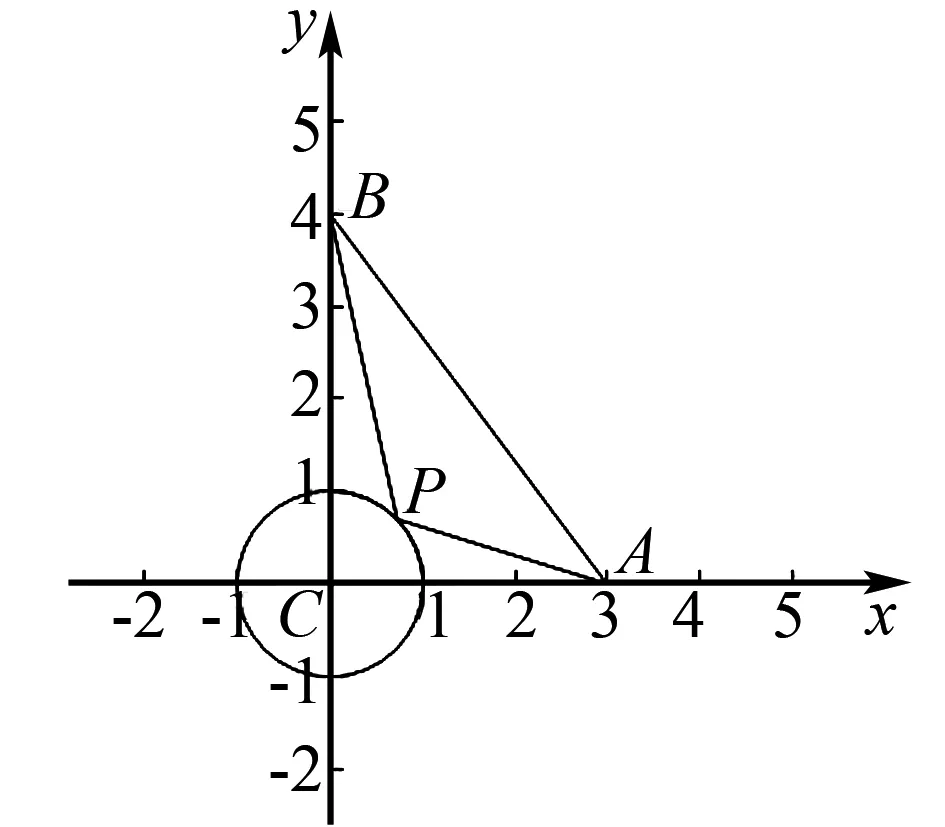
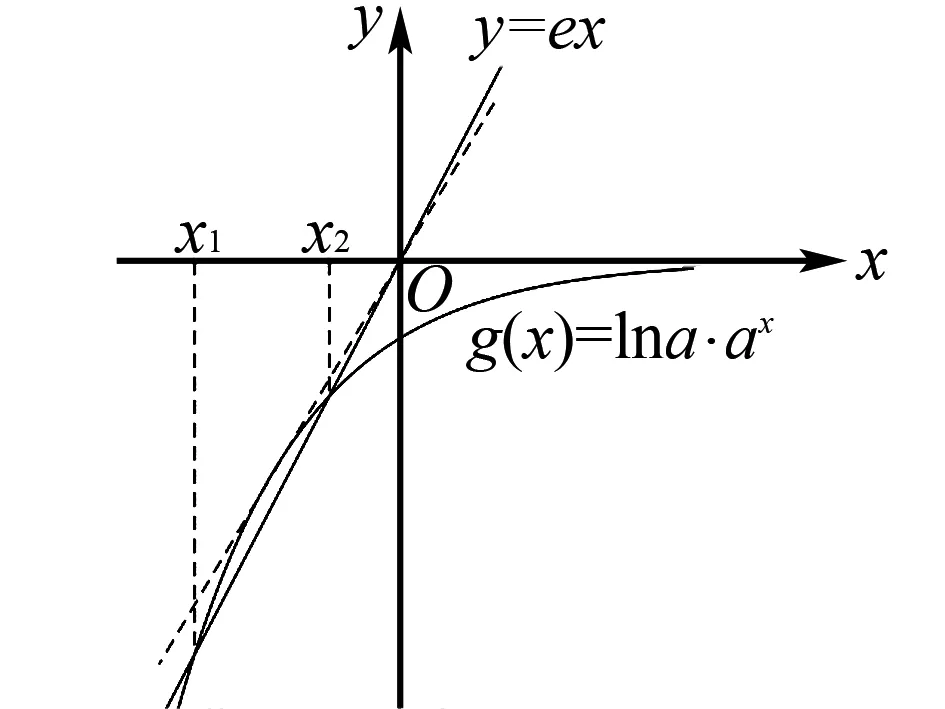
A.a C.c 当x∈(-1,0)时,f′(x)>0, 当x∈(0,+∞)时,f′(x)<0, 所以函数f(x)=ln(1+x)-x在(0,+∞)单调递减,在(-1,0)上单调递增. 故a 设g(x)=xex+ln(1-x)(0 令h(x)=ex(x2-1)+1, h′(x)=ex(x2+2x-1), 又h(0)=0, 所以g(0.1)>g(0)=0. 即0.1e0.1>-ln0.9,所以a>c 故选C. 例6(2022年全国高考甲卷理科第16题)已知x=x1和x=x2分别是函数f(x)=2ax-ex2(a>0且a≠1)的极小值点和极大值点.若x1 解析由题知f′(x)=2lna·ax-2ex. 因为x1,x2分别是函数f(x)=2ax-ex2的极小值点和极大值点,所以函数f(x)在(-∞,x1)和(x2,+∞)上单调递减,在(x1,x2)上单调递增.所以当x∈(-∞,x1)∪(x2,+∞)时,f′(x)<0,当x∈(x1,x2)时,f′(x)>0. 若a>1时,当x<0时,2lna·ax>0,2ex<0,则此时f′(x)>0,与前面矛盾. 故a>1不符合题意. 若0 因为0 又因为lna<0,所以y=lna·ax的图象由指数函数y=ax向下关于x轴作对称变换,然后将图象上的每个点的横坐标保持不变,纵坐标伸长或缩短为原来的|lna|倍得到,如图4所示. 图4 设过原点且与函数y=g(x)的图象相切的直线的切点为(x0,lna·ax0),则切线的斜率为g′(x0)=ln2a·ax0. 故切线方程为y-lna·ax0=ln2a·ax0(x-x0). 则有-lna·ax0=-x0ln2a·ax0. 例4、例5、例6分别通过构建一种数学函数模型的形式,把复杂问题简单化,重点考查学生的数学建模能力. 数学模式讲究数学问题的属性迁移,在数学模型维度解决,回归到认知的问题. 图5 图6 A. 0.75 B. 0.8 C. 0.85 D. 0.9 解析取OD1=DC1=CB1=BA1=1,则CC1=k1,BB1=k2,AA1=k3. 故k3=0.9,故选D. 例8(2022年北京高考卷第9题)已知正三棱锥P-ABC的六条棱长均为6,S是△ABC及其内部的点构成的集合.设集合T={(Q∈S|PQ≤5},则T表示的区域的面积为( ). 图7 因为PQ=5,故OQ=1. 故S的轨迹为以O为圆心,1为半径的圆. 而△ABC内切圆的圆心为O,半径为 故S的轨迹圆在△ABC内部,故其面积为π. 故选B. A. [-5,3] B. [-3,5] C. [-6,4] D. [-4,6] 解析依题意如图8建立平面直角坐标系,则C(0,0),A(3,0),B(0,4). 图8 因为PC=1,所以点P在以C为圆心,1为半径的圆上运动. 设P(cosθ,sinθ),θ∈[0,2π], =cos2θ-3cosθ-4sinθ+sin2θ =1-3cosθ-4sinθ 因为-1≤sin(θ+φ)≤1, 所以-4≤1-5sin(θ+φ)≤6. 例7、例8、例9分别通过把数学复杂问题回归数学模型,体现出高考命题注重应用性,增强试题灵活性,减少死记硬背和机械刷题,突出数学建模优势. 从以上2022年高考题得到数学建模本质,需要广泛知识面、高度开放性和灵活性,核心在于利用所学知识分析问题和解决数学问题的能力,进一步培养学生的数学建模能力.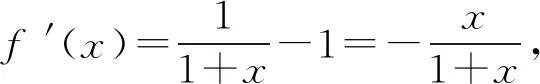
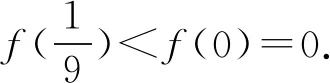
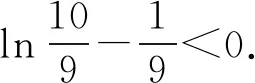
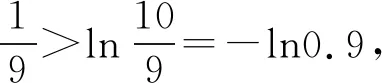
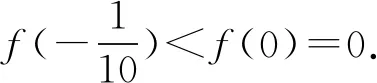

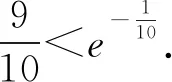
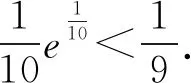
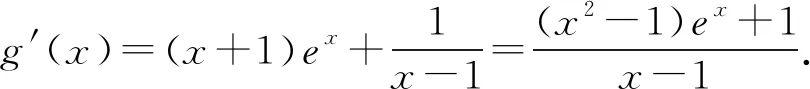
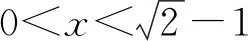
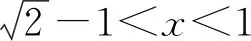
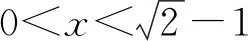
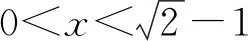

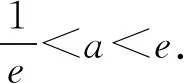
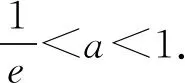
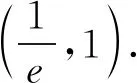
3 回归数学模型还原