多域特征提取和极限学习机的滚动轴承智能诊断

巴鑫宇，张义民，张 凯

（沈阳化工大学装备可靠性研究所，辽宁 沈阳 110142）

1 引言

滚动轴承在旋转机械中应用非常广泛，同时也经常容易出现故障，影响整个机器设备的正常运行，情况严重时可能会发生事故甚至给工作人员造成生命危险。因此及时判断滚动轴承的运行状态是非常有必要的。在实际复杂的工况下，由于受到负载、摩擦和冲击等因素的影响，滚动轴承的振动信号常表现出非线性以及非平稳特性，传统的方法很难提取出代表滚动轴承运行状态的故障特征。为有效提取轴承振动信号中的故障信息，我们通过多域特征提取方法获取原始振动信号的时域和频域特征，采用经验模态分解（Empirical Mode Decomposition，EMD）和变分模态分解（Variational Mode Decomposition，VMD）对原始振动信号进行分解得到一系列本征模态函数，计算其能量熵获得时频域特征，最后将时域、频域和时频域特征组合构造多域特征集[1-3]。

然而，多域特征集的维数比较高，存在大量无关特征，若直接采用分类器进行识别会降低识别准确率。为解决此问题，需要采用特征选择方法消除无关和冗余信息。

因此，我们采用Fisher得分算法（Fisher Score，FS）依靠特征相关性判别准则，先求出每个特征子集的得分，设定一个阈值，选择得分大于阈值的子集构成特征集，该方法具有计算量小，准确性高的特点[4]。在获得特征选择的多域特征集后，需要一个分类器来识别轴承的不同状态，从而建立一个智能诊断系统。近年来神经网络、支持向量机和隐马尔可夫等方法已经大量用于滚动轴承的智能故障诊断[1-2，5]。与这些方法相比，极限学习机（Extreme Learning Machine，ELM）[6]的优点主要是不需过多设置参数、泛化能力强以及学习效率快。因此本研究选用极限学习机作为智能诊断系统的分类器。

最后，利用实验数据验证，实验结果表明该方法对于现实复杂工况下的振动以及噪声问题，具有很高的辨识度。

2 EMD和VMD方法原理

2.1 经验模态分解方法

经验模态分解可以将复杂信号根据信号本身的特点按照频率由高到低顺序自适应的分解为一系列本征模态函数（Intrinsic Mode Function，IMF）。其中每个IMF 分量必须同时满足以下两个条件：（1）在整个时间序列中，过零点数和极值点数相同或者最多相差一个；（2）在任意时刻内，由局部极大值点和局部极小值点确定的上下包络线的均值必须为零[7]。

经验模态分解的过程如下：

（1）取待分解信号为x(t)的上下包络局部均值组成序列m(t)。信号与局部均值的差h1：

（2）当h1达到IMF分量的条件时，就将其视作x(t)的第一个IMF分量，即c1(t)=h1，并求出待分解信号与该IMF的差值r1(t)。反之重复步骤1）直到h1满足IMF 的条件并计算r1(t)。随后将r1(t)视为待分解信号，重复以上步骤，直到rn(t)满足预先给定的终止准则。

（3）最终将信号x(t)分解为n个IMF分量和一个余项之和的形式。

式中：ci(t)—第i个IMF分量；rn(t)—残余分量。

2.2 变分模态分解方法

变分模态分解（Variational Mode Decomposition，VMD）本质上相当于一种具有窄带特性的自适应维纳滤波器组，是近年来提出的一种自适应信号分解技术。VMD的基本原理是求解约束变分问题[8]，如式（4）所示。

为了求出每个IMF的带宽，需构建的受约束的变分模型如下：

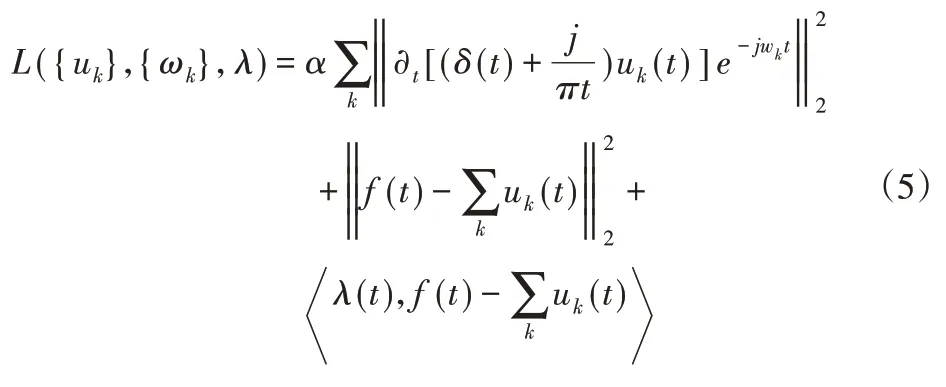
等式（5）可以利用交替乘子法求解，按照等式（6）和等式（7）更新模态函数和中心频率ωk。

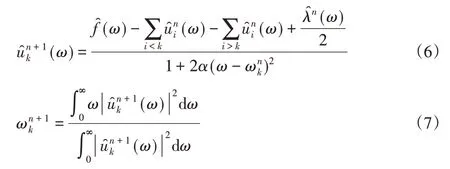
当固有模态函数和其相应的中心频率更新时，拉格朗日乘子λ按照等式（8）更新。

按照迭代更新，直到满足式（9）所示的收敛准则为止。

其中，常数ε通常设定为10-6。

2.3 Fisher得分算法

Fisher得分算法的目的是使降维后的数据样本类内距离最小，同时使类间的距离尽量大。首先设定数据集A中含有n类m个样本，其中第i个类有mi个样本。假设f为数据集其中的某个特征，则特征f的Fisher score为：

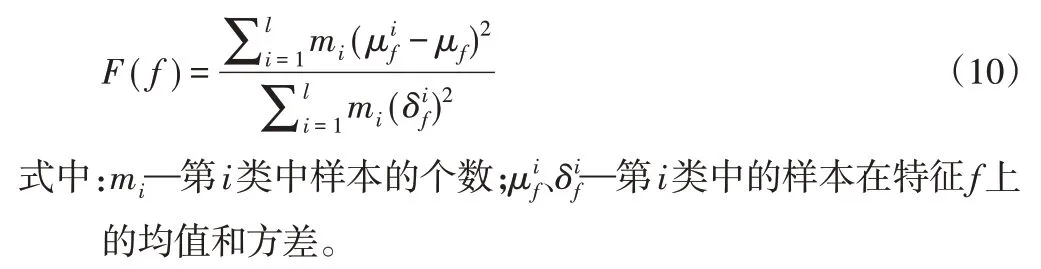
3 多域特征提取

当滚动轴承出现故障或缺陷时，通过分析振动信号在时域和频域上特征参数的变化差异，可以有效的辨别其运行状态。依据滚动轴承出现缺陷时，其特征参数会发生变化的特点，分别计算在时域和频域中反映滚动轴承状态变化的特征参数[2，9]，如表1、表2所示。

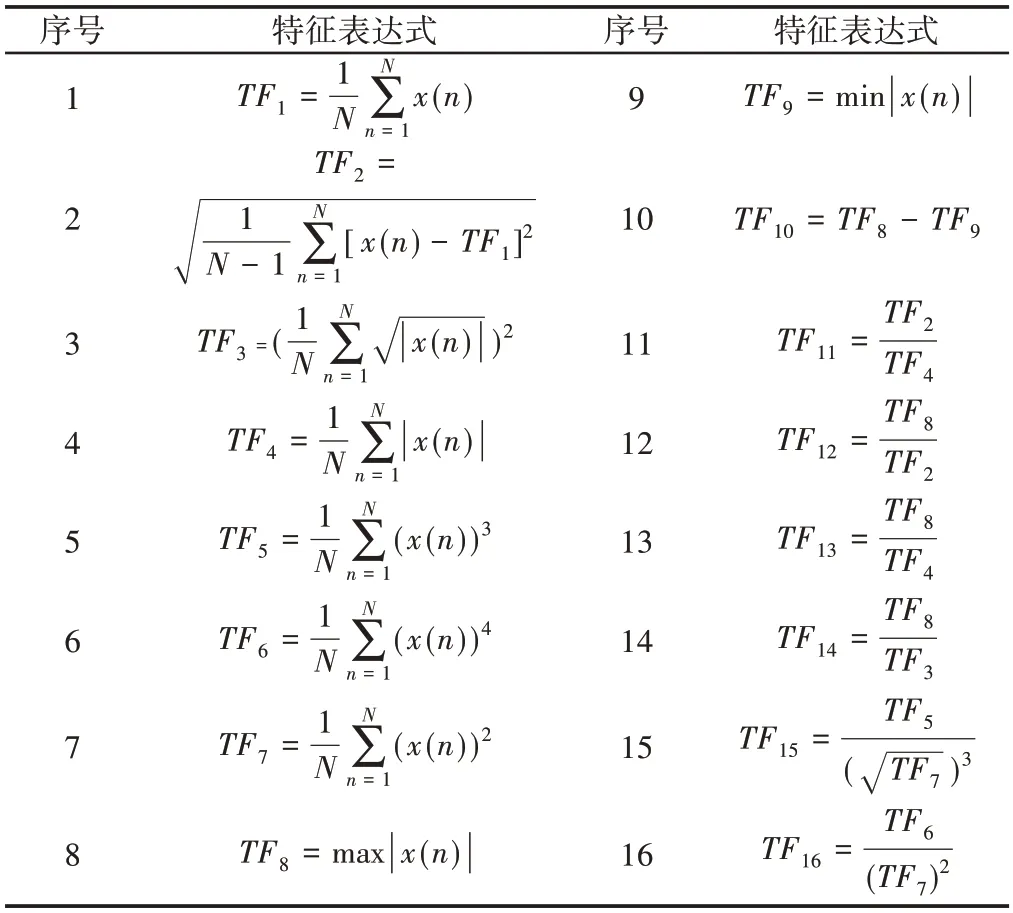
表1 时域特征表达式Tab.1 Time Domain Feature Expression

表2 频域特征表达式Tab.2 Frequency Domain Feature Expressions

时域特征主要反映振动信号的幅值波动、能量波动以及波形的分布情况。频域特征反映了主频带的分布情况以及频谱的分散和集中程度。仅仅计算时域和频域的特征参数难以全面准确的反映轴承的运行状态，还需提取振动信号的时频域特征。利用EMD和VMD对滚动轴承原始信号进行分解，计算其能量熵［7］。能量熵利用等式（11）计算：

式中：i=1，2，…，n。uk(t)—分解的IMF分量。

4 故障诊断流程

首先，采用多域特征提取方法提取原始振动信号的时域、频域以及时频域特征参数构造多域特征集。然后利用Fisher得分算法对多域特征集的特征按重要性排序，最后应用ELM分类器识别故障。其故障流程图，如图1所示。具体步骤为：

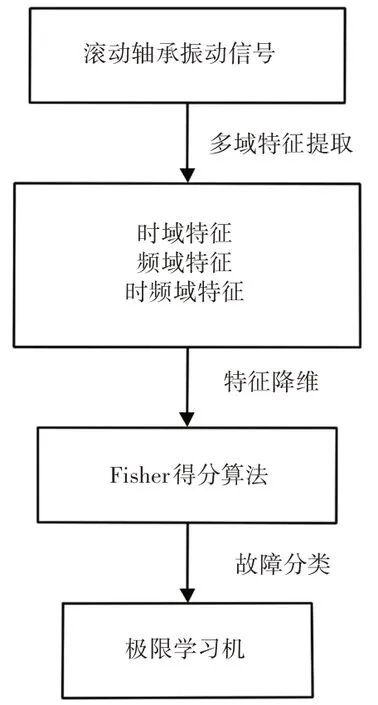
图1 基于多域特征提取、Fisher得分和ELM的滚动轴承故障诊断流程图Fig.1 Flow Chart of Rolling Bearing Fault Diagnosis Based on Multidomain Feature Extraction、Fisher Score and ELM

（1）收集滚动轴承不同运行状态的振动信号；

（2）应用多域特征提取方法获取多域特征集；

（3）利用Fisher得分算法对多域特征集的特征进行排名，取排名的前5的特征构造新的多域特征集；

（4）在新构造的多域特征集中，取每类样本的前1/3作为多域特征训练样本，将其余的样本组成多域特征测试样本；

（5）利用多域特征训练集对ELM训练，将多域特征测试集输入到训练好的ELM中进行分类识别。

5 实验验证

采用美国西储大学的滚动轴承试验数据验证该方法的有效性[10]。实验装置，如图2 所示。收集采样频率为12kHz，负载3HP，故障大小为0.1778mm、0.3556mm和0.5334mm工作条件下的滚动轴承振动信号，其具体参数，如表3所示。取每个工作条件下振动信号的前102400个数据点，平均分成50个数据样本，并且这些数据之间没有重叠。现实的工作条件经常伴随着振动和噪声，在滚动轴承原始信号加入50dB的白噪声以模拟复杂工况的现实条件，提高诊断模型的适应性和鲁棒性。

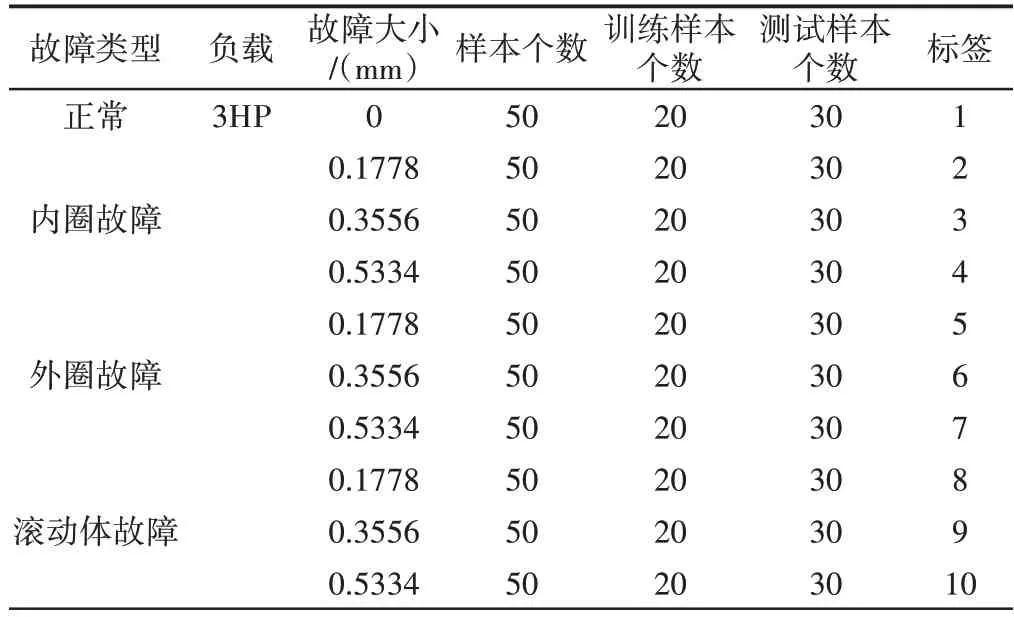
表3 实验样本数据Tab.3 Experimental Sample Data

图2 实验设备图Fig.2 Experimental Equipment Diagram

利用多域特征提取方法，直接从原信号中提取16个时域和13个频域特征。利用EMD和VMD对每段滚动轴承原始振动信号进行分解，VMD的分解层数这里取5，分别计算前5个IMF的能量熵，得到EMD和VMD分解出的10个时频域特征。将从每个样本中提取的39个特征组合在一起构成尺寸为（500×39）的高维多域特征集R，如等式（13）所示，将这些特征从（1～39）按照16个时域特征、13个频域特征、5个VMD分解的IMF的能量熵和EMD分解的前5个IMF的能量熵顺序排列。

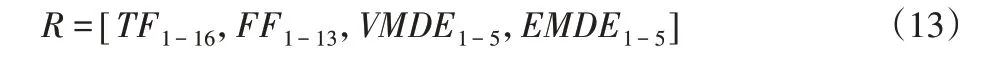
式中：TF1-16—16个时域特征；FF1-13—13个频域特征；VMDE1-5—VMD分解的5个IMF的能量熵；EMDE1-5—EMD分解的前5个IMF的能量熵。

然后利用Fisher得分算法对多域特征集进行排序，取序列前5构成新的多域特征集。将每类运行状态的前20个样本组成训练集样本，其余的组成测试样本。最后利用ELM进行分类识别。输出预测结果，如图3所示。分类的正确率为99.67%，由图可知，所有的故障类别大都得到了精准的分类，验证了方法对于含有噪声的复杂工况条件下的滚动轴承故障诊断方法的适应性和准确性。

图3 故障分类图Fig.3 Fault Classification Diagram

为研究Fisher得分算法和ELM分类器结合应用的有效性，采用不同的分类器进行比较研究。将通过Fisher得分算法得到的新的多域特征集和其他时域、频域和时频域特征集分别输入到BP[11]、随机森林（RF）[12]和KNN[13]这三种分类器中识别滚动轴承的故障类型。其中，BP神经网络的参数设定为：隐藏层神经元个数N=20，学习率α=0.1，最大训练次数I=500。KNN中的超参数K=3。

得到的诊断结果，如表4所示。该方法的平均准确率高于其他的单独时频域特征的准确率，表明多域特征集中含有更多可以代表滚动轴承运行状态的敏感特征信息，提高了分类精度。同时，与BP、随机森林和KNN的分类效果相比，表明了该方法具有更好的准确率和优越性。

表4 对比实验Tab.4 Contrast Experiment

分别采用Fisher得分算法和ReliefF算法[14]对多域特征集进行特征选择，依次选取（1～10）个特征的特征值构成特征集输入到ELM分类器。其实验结果，如图4所示。由图4可知，采用Fisher得分特征选择算法的准确率高于采用ReliefF算法，且Fisher得分算法选择4个特征时就可以达到很高的准确率，这说明了Fisher得分算法在挖掘故障特征信息方面具有更大的优势；模型的正确率随着选择敏感特征数目的增加而增加，而当敏感特征数目的继续增加时，正确率反而下降。这说明敏感特征个数过少不能很好的代表故障的敏感特征信息，而太多会过拟合，降低了计算精度。因此，证明了Fisher得分算法的优越性以及选择合适的敏感特征数的重要性。

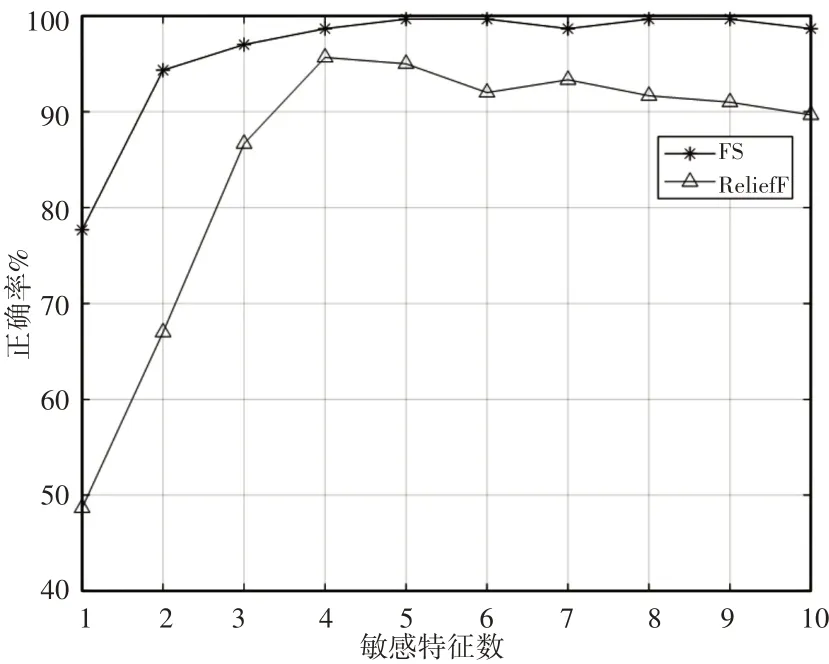
图4 选择不同敏感特征数目的正确率Fig.4 Select the Correct Rate for the Number of Different Sensitive Features

6 结论

针对复杂工况下采集的滚动轴承的振动信号中含有振动和噪声的情况，提出了基于多域特征提取、Fisher得分和极限学习机的智能诊断方法。与传统的特征提取相比，多域特征提取的故障特征信息可以全面、精准的代表滚动轴承的运行状态。提出的方法优点是，克服了复杂工况下的噪声问题，去除高维特征向量中的扰动和冗余信息，提高样本的可分性和准确率。