真实刀刃轨迹下的涡旋齿周铣瞬时厚度模型
2022-09-22王鸿宇孙永吉
刘 涛,王鸿宇,孙永吉,2
(1.兰州理工大学机电工程学院,甘肃 兰州 730050;2.兰州工业学院,甘肃 兰州 730050)
1 前言
涡旋盘是涡旋流体机械的关键零部件,其上涡旋齿具有型线构成复杂、壁薄、刚性弱、表面精度高等特点。高速圆周铣削是实现涡旋齿侧壁面高精度高效率加工的重要方式。在较小加工余量下,刀具结构和加工零件的型面特征对铣削过程和表面质量的影响作用凸显,精加工切削用量选择不当会对涡旋齿铣削加工质量造成较大影响。因此,研究铣削过程中的刀刃轨迹及瞬时铣削厚度变化规律,可为复杂曲面涡旋齿小切削用量精铣加工的切削用量选取提供理论依据和参考,更好地实现精加工表面精度控制[1]。
铣削厚度一般通过铣刀刀刃在待切工件上划过的轨迹来计算,真实的刀刃轨迹可以保证铣削厚度的计算精度。针对传统圆轨迹铣削厚度计算公式存在一定误差的情况,文献[2]提出了基于次摆线轨迹的铣削厚度及其误差计算方法,并与传统圆轨迹方法进行了对比。文献[3]将真实的刀刃切削轨迹引入不同的加工特征以分析切削厚度。文献[4]基于真实刀刃轨迹通过几何法对瞬时切削厚度进行了计算。文献[5]通过求解超越方程计算未变形切削厚度。上述研究对象均为铣刀中心相对工件沿直线运动的铣削过程,对于铣刀中心沿圆弧轨迹运动的情况,文献[6]的研究表明基于每齿进给量的铣削厚度简化公式只适用于圆轨迹半径比较大的情况。文献[7]对涡旋齿侧壁面径向铣削厚度进行了研究。文献[8]的研究表明圆周铣削时刀具包络面各点的进给率与刀具轨迹半径及点到切削中心的距离有关。
为实现复杂型面薄壁涡旋齿高精度、高效率铣削加工,文献[9]研究可知刀具走刀方式和间距对加工质量有重要影响。文献[10]利用Taylor展开的数值方法计算得到真实刀刃轨迹下的瞬时厚度近似值。但考虑涡旋齿内、外侧壁型面特征及圆周铣削过程刀刃轨迹等因素的铣削厚度模型尚未见文献报道。
推导了涡旋齿加工过程的真实刀刃轨迹,将几何法[4]进行改进得到圆周铣削瞬时厚度数学模型,并与基于轨迹坐标的厚度计算方法进行对比,定量研究了工件、刀具和铣削参数等因素对铣削厚度的影响。研究结果对考虑刀具参数和型面特征影响的涡旋齿精铣加工切削用量选择具有重要参考价值。
2 真实刀刃轨迹
铣削过程中刀刃的运动轨迹是研究瞬时铣削厚度的基础。在直线铣削过程中,刀具中心的轨迹为直线,如图1(a)所示。对于图1(b)所示圆周铣削过程,刀具中心轨迹为圆弧,直接采用直线铣削厚度计算公式会产生较大误差,故需确定圆周铣削时刀刃的真实轨迹并据此计算瞬时铣削厚度。
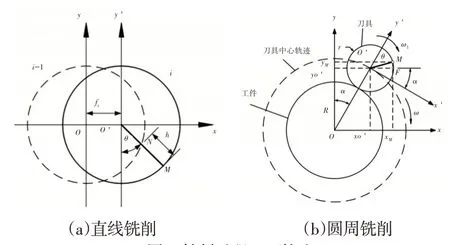
图1 铣削过程刀刃轨迹Fig.1 Tool Path in Milling Process
建模刀具采用铣削加工常见的圆柱立铣刀,设刀具半径为r,刀刃过中心;刀齿数(刀刃数)为Z,刀齿均匀分布。
2.1 圆周铣削坐标系定义
定义图1(b)中直角坐标系xOy为定坐标系,O为被加工圆盘形工件圆心,同时是定坐标系原点;x′O′y′为动坐标系,原点在铣刀中心轴线上。初始时刻y′与y轴重合。
立铣刀沿顺时针方向以角速度ω绕工件做圆周运动,同时以自转角速度ω1切削工件,则刀刃上任一点M相对于固定工件坐标系xOy的运动为绝对运动,M点相对于刀具坐标系x′O′y′的运动为相对运动,刀具相对于固定工件的运动为牵连运动。铣刀刀刃上任一点M划过的路径即为所求真实刀刃轨迹。
2.2 刀刃运动轨迹
由图1(b)可知,刀具中心O′在定坐标系xOy下的坐标为:

其中,α—刀具中心沿圆周转过的角度,α=ωt;R,r—工件半径与刀具半径。则动点M在定坐标系xOy(绝对坐标系)下的坐标为:
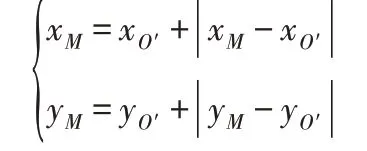
即M点随时间变化的运动轨迹方程为:
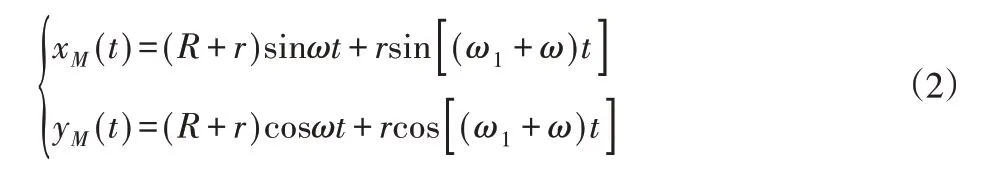
式中:(ω1+ω)t—时间t内刀刃上一点M到刀具中心的连线相对于定坐标系y轴转过的角度。通过方程(2)可知,刀刃真实的轨迹为特殊摆线。采取同样方法可得加工涡旋齿内壁时的刀刃轨迹方程为:
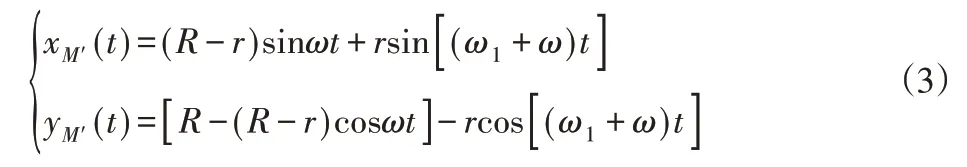
根据轨迹方程式(2)及式(3)可知,刀刃真实轨迹形状为特殊摆线,与直线铣削采用的圆轨迹有所差别。圆周铣削加工过程刀刃轨迹的形状取决于被加工工件半径R、铣刀刀具半径r、刀具角速度ω1及刀具绕工件进给角速度ω等参数。
3 涡旋齿圆周铣削厚度模型
3.1 传统方法
直线铣削瞬时铣削厚度采用经典公式:
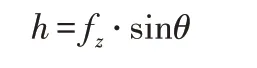
式中:fz—铣刀每齿进给量;θ—刀具中心角。
如图1(a)所示,i—当前刀刃轨迹;(i-1)—前一刃轨迹,刀刃过M点,且与前一刃轨迹相交于点N,|MN|即为两刀刃间的瞬时铣削厚度。该方法假设刀刃轨迹为圆,适用于每齿进给量fz较大的情况。圆周铣削时刀刃轨迹特殊,传统方法不再适用,需采取更为合适的方法计算瞬时铣削厚度。
3.2 改进的几何法
外圆周铣削为例,如图2所示。零时刻开始,铣刀沿工件圆周顺时针转过的角度为α,该时刻铣刀第i刃经过点M,刀刃转角为θ,与前一刃切削过的轨迹相交于点N,|MN|即为该时刻瞬时铣削厚度。
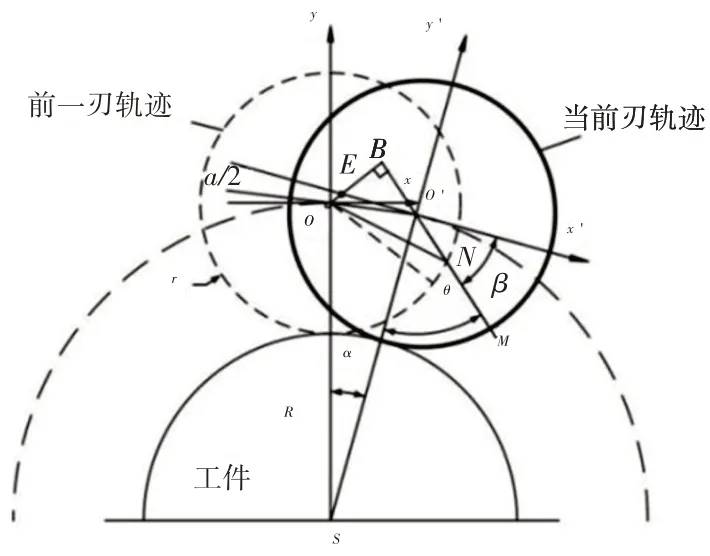
图2 几何法计算瞬时铣削厚度Fig.2 Calculation of Instantaneous Milling Thickness by Geometric Method
延长MN至B与OB垂直相交,连接OO′,得到∠OO′E=∠EO′B=β,则∠OO′B=α/2+β。由余弦定理得:
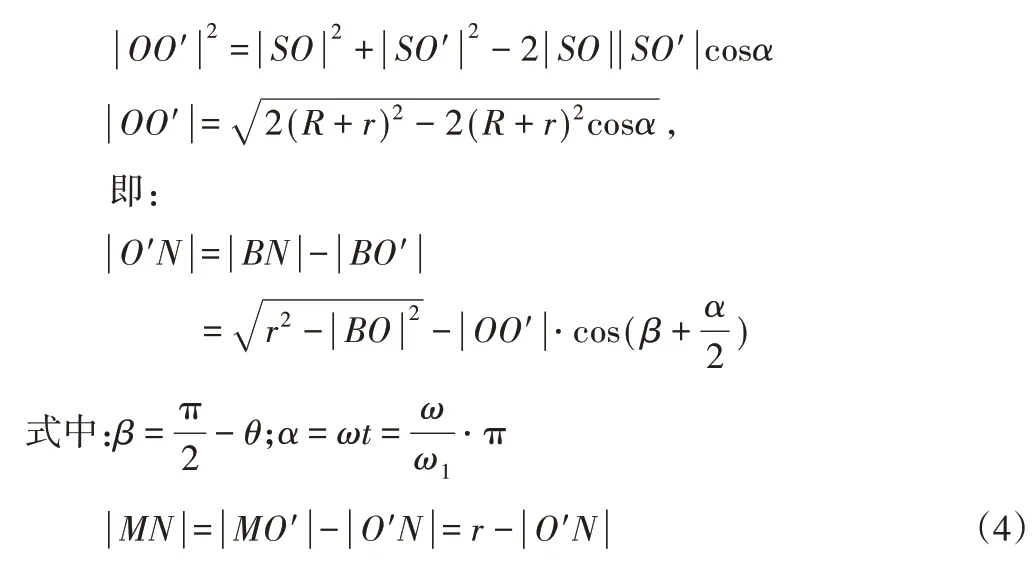
将各参数代入式(4),得到瞬时铣削厚度h的表达式为:
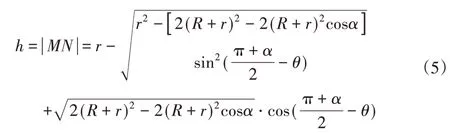
3.3 基于真实刀刃轨迹法
上述厚度计算模型是基于切削点的几何位置关系得出,以下基于铣刀刀刃真实轨迹坐标计算瞬时切削厚度。
3.3.1 铣削涡旋齿外壁
如图3(a)所示,当前铣削刃过MN位置时刻的刀刃转角为θ,前一刃过N点时刻的刀刃转角为(θ+δ),则两相邻铣削刃转角相位差为δ(θ),由文献[6]可知:
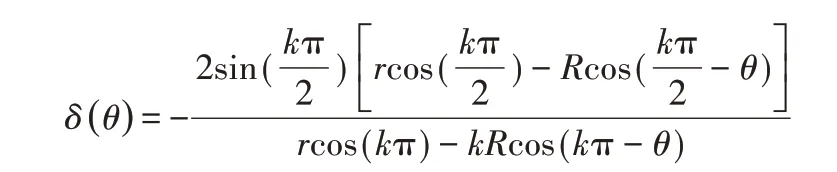
式中:k=fZ/2πR,其中,f=R⋅α。
设前一刃初始位置与y轴重合,过N点时刻为t0,则:

将式(6)代入前文得到的真实轨迹方程式(2),得到t0时刻N点的真实坐标值。
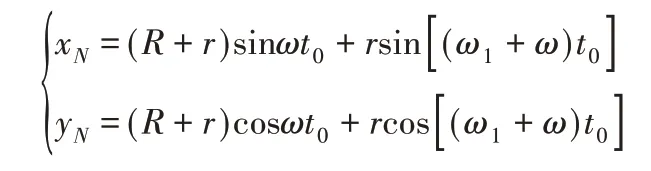
设相邻刀齿间的齿间角φc=2π/Z,下一切削刃过MN时刻为t1,则:

将式(7)代入式(1),得到t1时刻刀具中心O′的位置坐标:
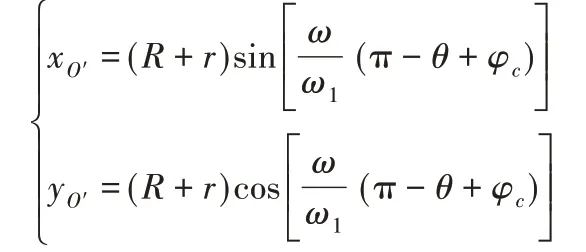
则基于真实轨迹坐标的瞬时铣削厚度为:
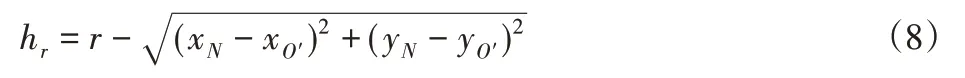
3.3.2 铣削涡旋齿内壁
由图3(b)可知,铣削内壁与铣削外壁的区别在于刀具中心O′与工件中心O的距离发生了变化,即计算刀具中心点坐标O′的公式发生变化;同时将式(6)代入铣削内壁轨迹式(3),通过式(8)即可得到铣削涡旋齿内壁时的瞬时铣削厚度。
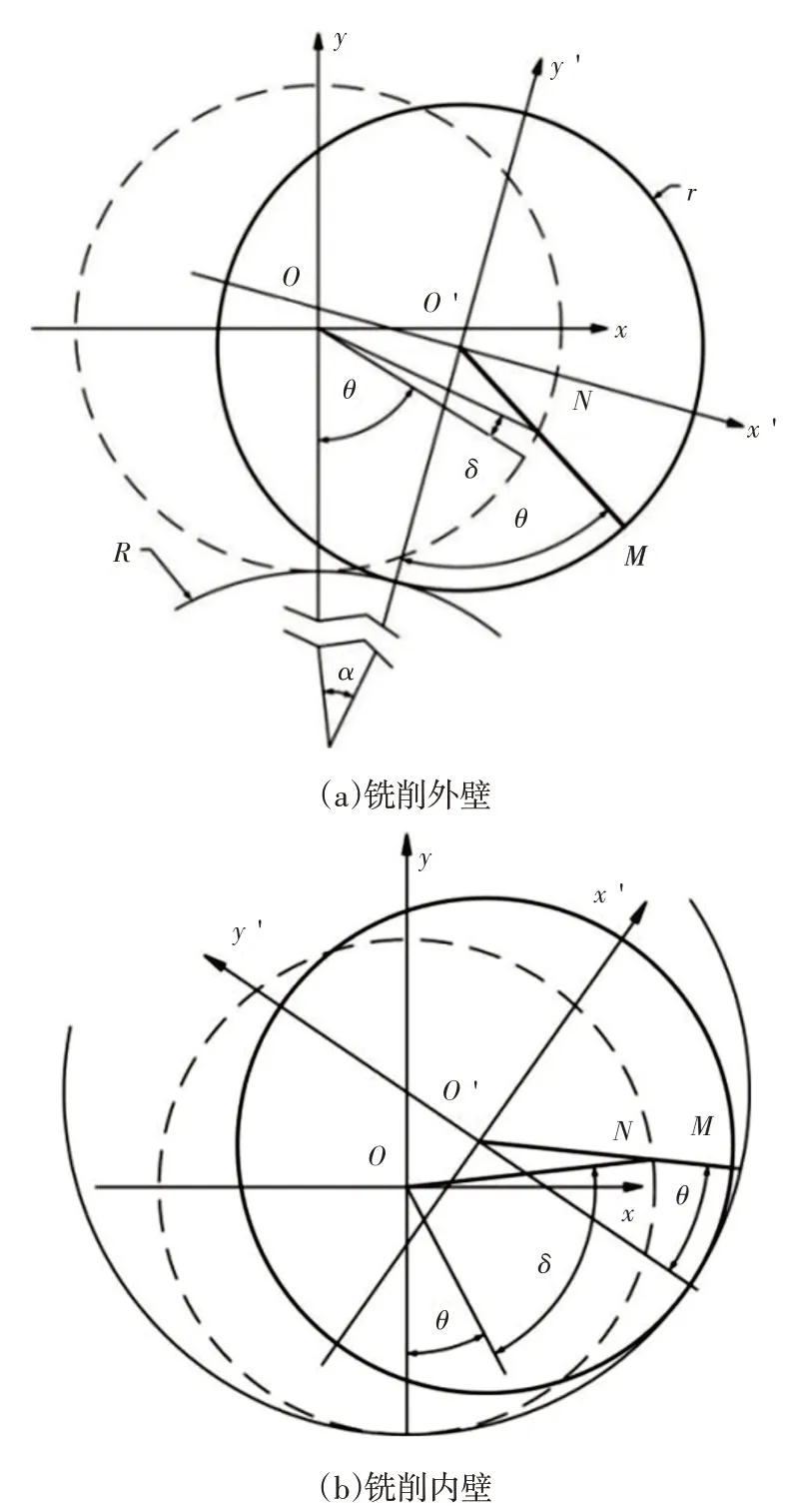
图3 铣削涡旋齿内、外壁表面Fig.3 Milling the Inner and Outer Surface of Scroll Teeth
4 涡旋齿瞬时铣削厚度影响因素分析
刀具参数、工件参数及刀具工件相对运动参数是影响加工表面精度的三个重要因素。针对涡旋齿精铣加工工况,选取一组参数作为初始条件对涡旋齿内外壁瞬时铣削厚度进行数值计算,参数选择,如表1所示。

表1 涡旋齿铣削加工参数Tab.1 Machining Parameters of Scroll Teeth Milling
4.1 涡旋齿铣削厚度随刀刃转角变化情况
由式(5)可知,瞬时铣削厚度h与工件半径R、铣刀半径r、刀具沿圆周进给角速度ω、刀具旋转角速度ω1及刀刃转角θ等均有关系。在一定的加工条件下,R、r、ω、和ω1等均为定值,故厚度h随刀刃转角θ变化而变化。采用直线铣削公式法、圆周铣削几何法及基于真实轨迹坐标铣削厚度计算方法得到的涡旋齿内外壁瞬时铣削厚度随刀刃转角θ的变化规律,如图4所示。
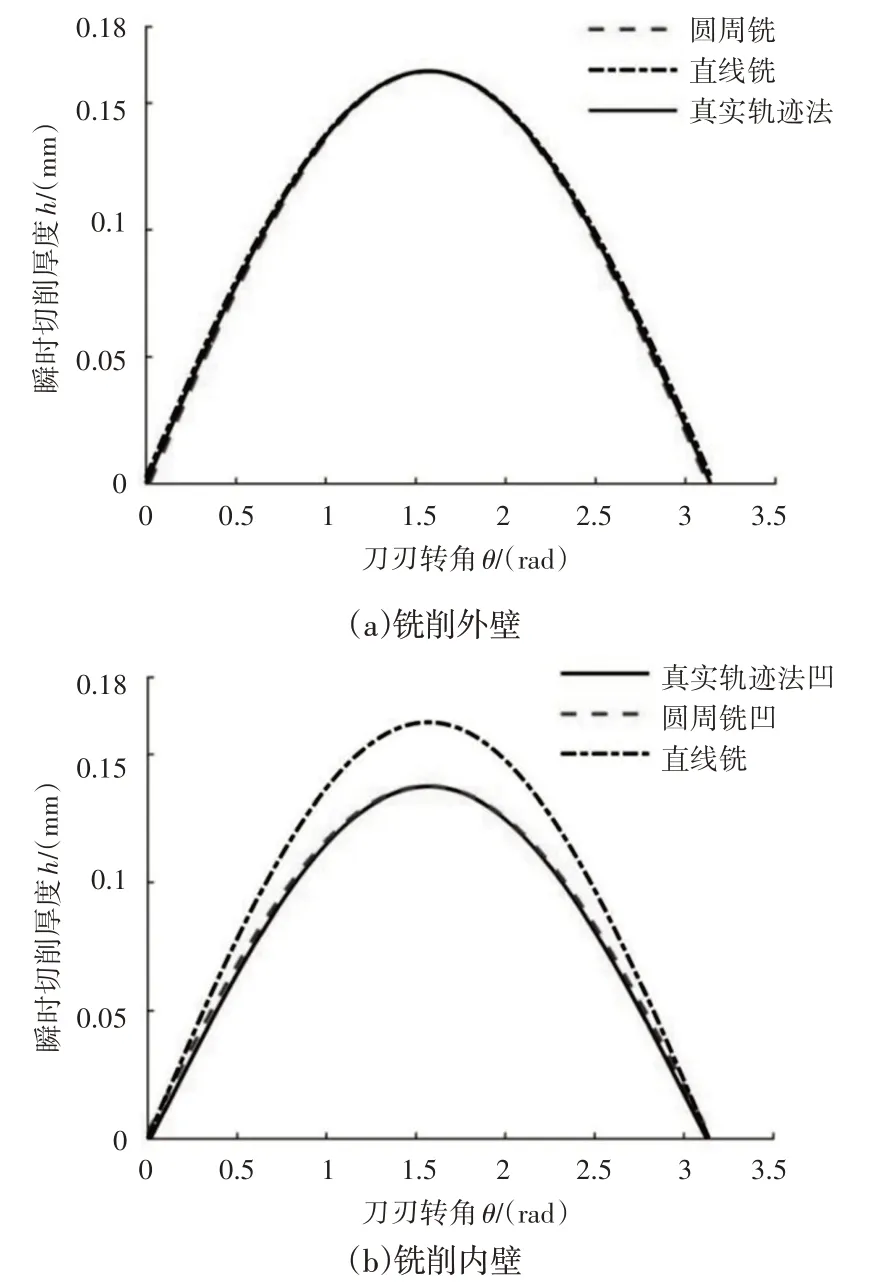
图4 几种不同厚度计算方法结果对比Fig.4 Comparison of the Results of Different Thickness Calculation Methods
由图4(a)可知,三种方法计算出的外壁铣削厚度变化趋势相同,瞬时铣削厚度先增大后减小。在θ∈(0,1.3)时直线铣削公式法得到的铣削厚度最大,圆周铣几何法厚度最小;θ∈(1.3,2.0)范围内,三者计算出的铣削厚度几乎相同。
利用真实轨迹法模型计算涡旋齿外壁面铣削厚度时,刀具中心角位置θ=1.6rad对应的瞬时铣削厚度最大,约为0.162mm。
图4(b)所示,在铣削涡旋齿内壁面时,直线铣削公式法厚度最大值比几何法和真实轨迹法高出约27%,说明在内壁面铣削厚度计算中传统的公式法误差较大,已不再适用。
同一刀刃转角θ下,外壁面瞬时铣削厚度均大于内壁面瞬时铣削厚度,当θ=1.6rad时,内、外壁铣削厚度差值达到最大,内壁瞬时铣削厚度比外壁铣小21%。
造成这一现象的原因是内壁面铣削时由于刀具绕工件圆周运动半径缩短,导致相邻两铣削刃划过的轨迹间距缩小,各刀具中心角度对应的瞬时铣削厚度也随之减小。
4.2 铣削厚度随涡旋齿型线曲率半径变化情况
刀具中心转角θ=π/4时,涡旋齿型线曲率半径R由50mm增大到70mm的过程中涡旋齿内外壁面瞬时铣削厚度的变化情况,如表2 所示。可知随着曲率半径增大,瞬时铣削厚度呈增大趋势,内外壁铣削厚度差值在(15~22)%的范围内变化,说明圆周铣削过程中内、外壁铣削瞬时切削厚度差值明显,在实际加工中应分情况考虑。
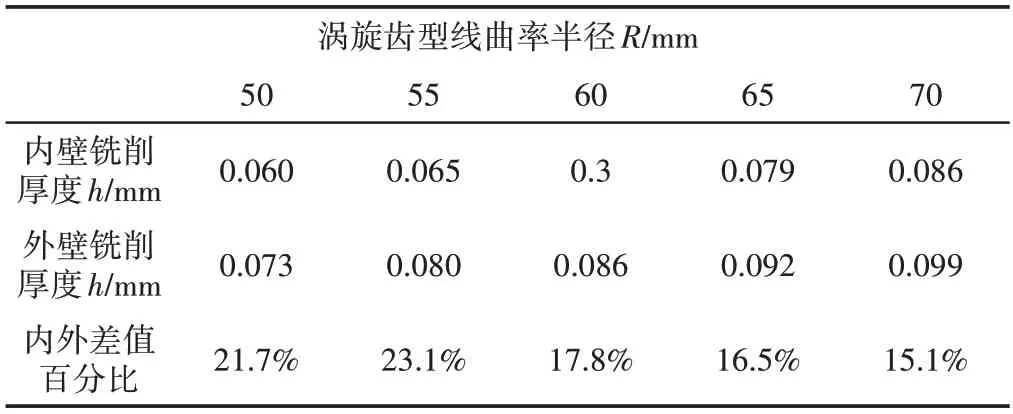
表2 不同型线曲率半径内外壁铣削厚度值Tab.2 Milling Thickness of Inner and Outer Wall with Different Curvature Radius of Profiles
4.3 铣削厚度随刀具齿数变化情况
刀具齿数Z分别为2、3、4齿时,同一刀刃转角下的瞬时铣削厚度不同,刀刃齿数越少,瞬时铣削厚度越大,如图5所示。当刀刃齿数为3和4时,瞬时铣削厚度在一定刀刃转角范围出现负值,说明其他参数不变,齿数增加会导致部分刀刃转角出现“空切”现象,即当前刀刃在部分转角范围划过的轨迹被前一刃划过轨迹包含,“空切”会导致功率损失,应当避免。
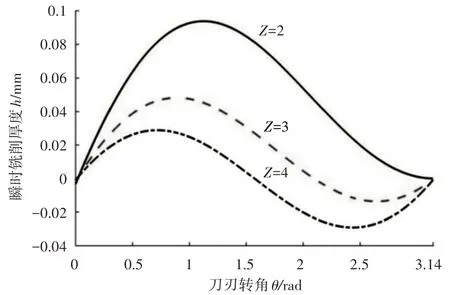
图5 瞬时铣削厚度与刀具齿数的变化关系Fig.5 Relation Between Instantaneous Milling Thickness and Teeth Number
4.4 铣削厚度与进给角速度及刀具角速度的关系
主轴角速度恒定时,刀具进给角速度对瞬时铣削厚度的影响,如图6(a)所示。铣削外壁时,进给角速度由0.1rad/s 增大到0.4rad/s 的过程中,瞬时铣削厚度由0.035mm 线性增大至0.14mm。增大进给角速度会显著提高加工效率,但同时导致刀具受力增大而产生振动,需合理选取进给速度。
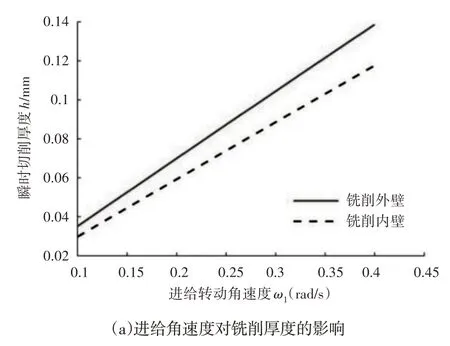
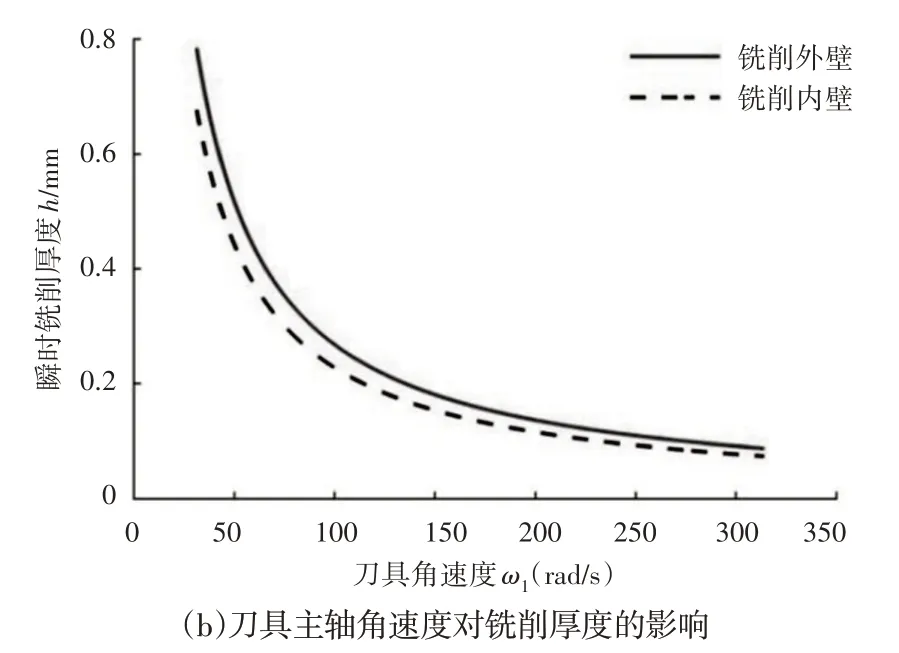
图6 瞬时铣削厚度与进给转速和刀具主轴的关系Fig.6 The Relation Between Instantaneous Milling Thickness and Feed Speed and Tool Spindle Speed
图6(b)所示当主轴角速度从10πrad/s逐渐增大到100πrad/s(主轴转速从300 r/min增大到3000 r/min),瞬时铣削厚度呈减小趋势,外壁铣削厚度均略大于内壁,且角速度ω1∈(10π,100)厚度减小趋势最为明显;当角速度增大到100rad/s以上时,瞬时铣削厚度值的减小速率逐渐放缓并趋于稳定,可知在涡旋齿实际加工过程中将机床主轴转速设置在3000r/min以上可得到较小铣削厚度,从而提高表面加工精度。
5 结论
通过定义刀具参数和相对运动坐标系建立了圆周铣削工况下刀刃的真实轨迹方程,分别采用改进的几何法和基于真实刀刃轨迹的方法建立了圆周铣削工况下的瞬时铣削厚度数学模型,该模型可用于在涡旋齿内外壁面瞬时铣削厚度的计算。研究了刀具中心转角θ、涡旋齿曲率半径R、刀刃齿数Z、进给角速度ω及主轴角速度ω1等因素对铣削厚度影响。
(1)建立的模型综合考虑工件、刀具和铣削参数等的影响,较传统直线铣削瞬时厚度计算方法更能准确反映内外壁铣削厚度的变化规律。
(2)随着中心转角θ的增大,瞬时铣削厚度先增大后减小,刀具中心角位置θ=1.6rad 时瞬时铣削厚度达到最大值0.162mm,同时内外壁铣削厚度差值达到最大,内壁铣瞬时铣削厚度比外壁小21%;随着涡旋齿型线曲率半径增大,瞬时铣削厚度呈线性增加;刀刃齿数越少,瞬时铣削厚度越大;进给角速度由0.1rad/s增大到0.4rad/s,瞬时铣削厚度由0.035mm 线性增大至0.14mm;主轴角速度增大到100πrad/s以上时,瞬时铣削厚度趋于稳定。建立的铣削厚度计算模型可为复杂型面涡旋齿精铣削加工切削用量的选取提供理论依据。
