基于无网格方法的滚动球轴承温度场分析

董永兵，张义民，李铁军

（1.沈阳化工大学装备可靠性研究所，辽宁 沈阳 110142；2.沈阳化工大学能源与动力工程学院，辽宁 沈阳 110142）

1 引言

轴承在现代机械传动部件中有十分重要的地位，随着科学技术不断向前发展，对现代机械的使用寿命和运行精度的要求越来越高，因此也使得人们对轴承的高精度和长寿命的需求越来越大[1]。但轴承在工作中，尤其是在恶劣的工况下，由于其内各部件摩擦产生的巨大热量使得轴承工作温度异常升高，各零件受热变形后直接影响传动部件的工作精度和轴系的使用寿命，严重的会产生轴承沟道和滚动体烧伤甚至抱死现象。因此准确及时的获得轴承内部温度分布，可以对整个传动系统进行合理设计，对轴系部件实时调整使用工况，使得因温度升高而易失效处得到合理散热与润滑，提高整个机械的使用精度、可靠性和寿命。所以建立滚承的传热模型，准确快速的分析出轴承温度场分布就显得十分重要。

目前分析方法轴承温度场的方法主要有热阻网络法、有限元法以及实验法，文献[2]应用热阻网络法建立传热模型计算轴承温度场，得出部分节点的温度变化规律。但该种方法不便处理复杂形状，并对内部温度分布不能很好反应；文献[3]以传热学为理论基础，应用有限元法（FEM）分析出轴承稳态温度场，由于需要对网格进行合理划分，对问题的求解难度和计算量较大，求解速度较慢。考虑采用无网格法对轴承温度场进行计算。

近几年来，无网格方法快速向前发展，从开始应用于计算力学逐步拓展到包括数值传热学等诸多领域。对比于FEM来说，无网格法只依靠离散节点的信息，避免了复杂的网格生成过程，同时也避免了低质量网格对计算结果的影响，可以较为简单的描述不规则的几何形状，保证计算精度的基础上，节省了大量时间。文献[4]用无网格Galerkin 方法（EFG）计算热传导问题，计算结果表明其具有较快的收敛速度，但由于采用背景网格积分，所以EFG不是真正的无网格方法。文献[5]采用移动最小二乘法（MLS）构建试探函数，将无网格Petrov-Galerkin法（MLPG）应用在非稳态导热中，得到了较好的计算结果。文献建立了加权最小二乘无网格法（MWLS）并成功应用到稳态与非稳态数值传热中，计算结果表明该方法是一种精度高、速度快的数值传热分析方法。目前尚未发现将无网格传热方法应用于轴承非稳态温度场计算。

根据滚动轴承温度场分析和无网格法发展现状，将MWLS应用于深沟球轴承温度场构建，推导了相应的计算公式，并编辑了相应的程序，解决了有限元方法计算量大和计算时间较长的问题，得到了较为理想的结果。

2 无网格方法的实现

2.1 移动最小二乘近似

设待求函数u（x）在全域Ω内分布有N个点，I=1，2，…N，且给出各节点处函数值，即uI=u（xI）。函数u（x）的近似表达式为uh（x），函数uh（x）在计算点x处的求解邻域Ωx内可以用式（1）表示［6-7］：

式中：pi（x）—基底函数，基底函数的构造常采用多项式形式；m—基底函数的数量；ai（x）—基底函数对应待定系数—计算点x的邻域Ωx内节点坐标，p(x)=

在MLS近似中，ai（x）是在点x处的邻域Ωx里通过使局部近似表达式uh(x，)与函数u（x）之间差的平方最小化得到，即对各个节点差值的加权平方之和取最小值，假设计算点邻域有n个节点，由此可以列出如下表达式：

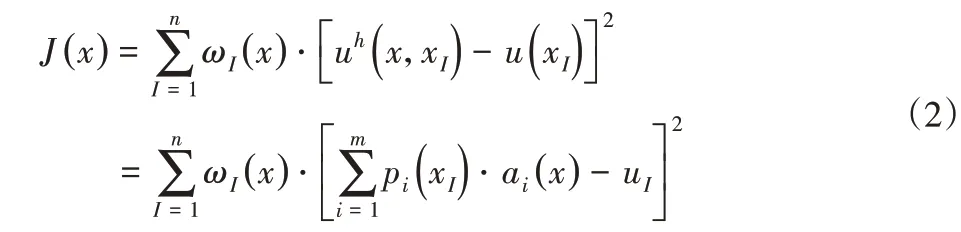
式中：ωI—非负权函数，与xI点相关，在点xI处权函数值取最大值，在支撑域边界及域外权函数取值最小，即ω（r）=0，其中r=d/dmI，d—点x到节点xI之间的距离；dmI—权函数支撑域半径，有dmI=s·c；s—支撑域半径系数；c—节点之间距离。选取三次样条权函数，即：

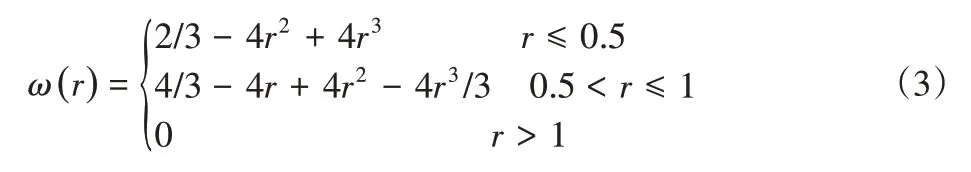
对J（x）其取极小值：

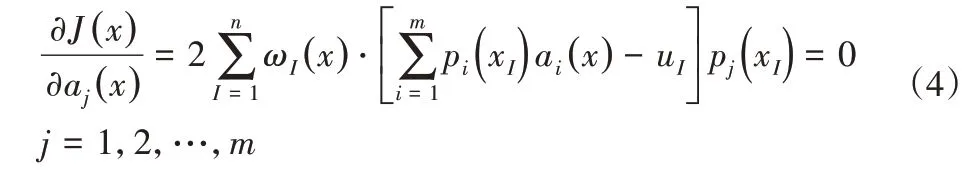
整理可得：

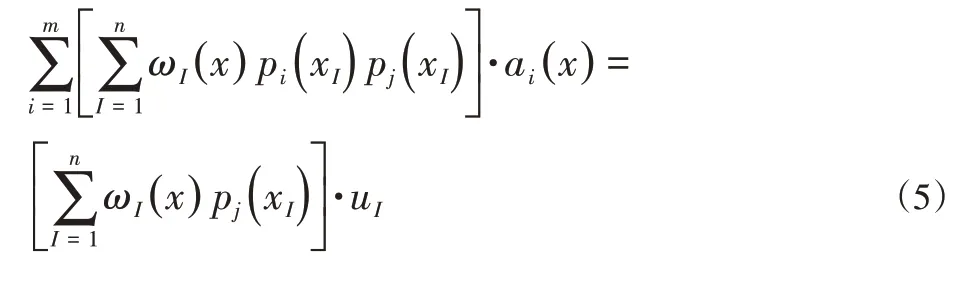
由式（5）可以解出待定系数向量a（x）：

其中，

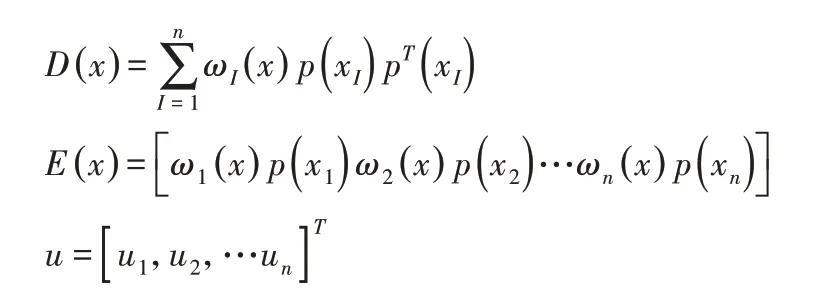
将a（x）带回式（1）可得到：

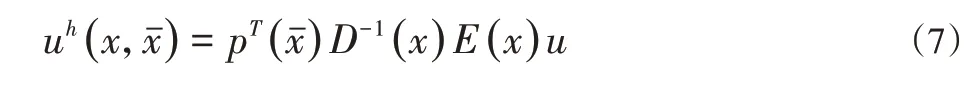
如果对全域Ω中所有点x都在邻域Ωx内构造上述局部最佳近似表达式，将其组合后就得到了待求函数u（x）在求解域Ω内的全局最佳近似函数uh（x），即：

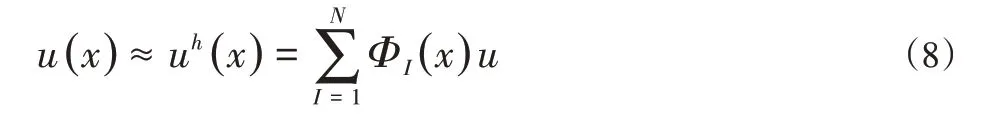
其中，形函数ΦI（x）为：

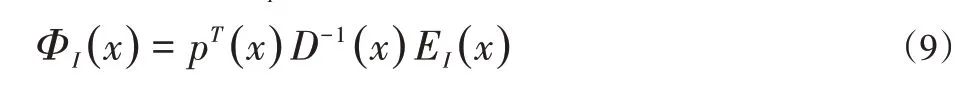
其中，EI（x）—矩阵E（x）的第I列。

2.2 非稳态传热中MWLS模型构建

计算对象的温度场随时间而发生变化的导热过程为非稳态导热，如假定材料导热系数不随温度变动，即为常数时，则其热微分方程为［8-9］：

边界约束条件可以表示为：

对于非稳态情况，指定初始条件：

式中：k—材料的导热系数；ρQ—热源项；n—各边界面外法线方向—第一类边界Γ1上的规定的温度—第二类边界Γ2上沿n方向的热流密度；h—表面散热系数；Tw—周围温度；ρ为材料密度；c—材料比热。

对于非稳态导热问题涉及对时间求导数，因此采用向后差分改写控制式（10）可得：

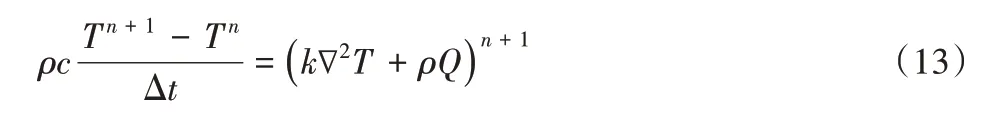
假设热源项不随时间改变，经过整理可将式（13）改写为：

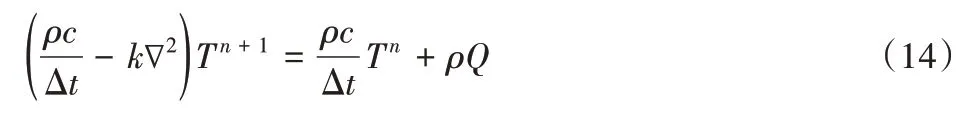
式中：n—时间步长，式（14）左面第（n+1）个时间步长的结果可以完全由第n个时间步长的结果唯一确定，可以按照MWLS方法求解。

MWLS是以加权残量的方式来求解偏微分方程，定义非稳态传热的全域和各边界的残量为R和Ri（i=1，2，3），其残量表达式为：

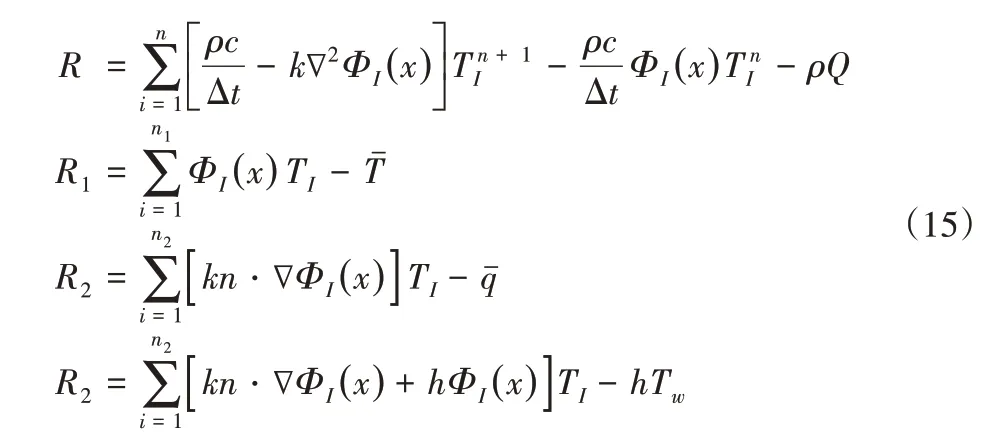
将式（15）中各残量分别平方并加权积分后相加，可得到如下泛函：

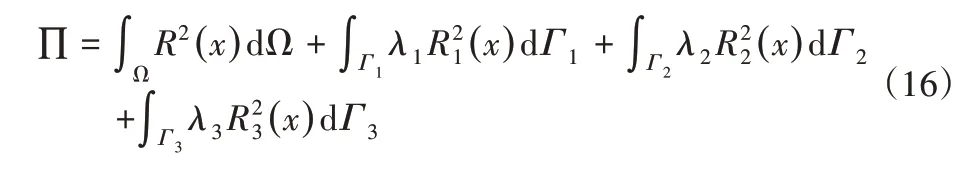
由于积分的计算量较大，采取离散的方法将其泛函改为：

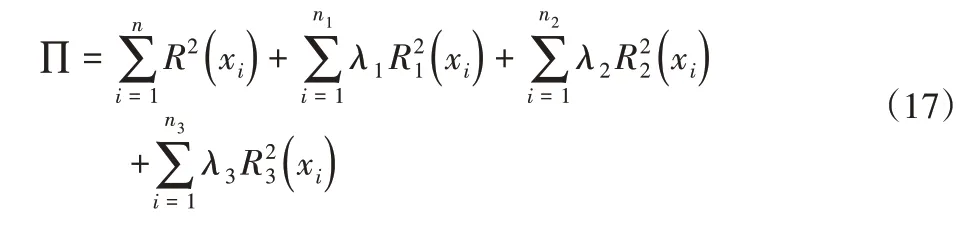
式中：λs（s=1，2，3）表示三种约束边界条件所对应的罚函数；n—控制式（10）的残量的计算节点个数；nl（l=1，2，3）为各自对应约束条件残量的计算节点个数，对式（17）的泛函取极小值，即：

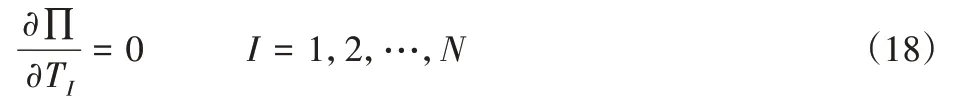
可以得到求解非稳态传热方程的加权最小二乘无网格方法（MWLS）的系统方程，并用简单的迭代可以解出各个时刻的温度分布：

其中，

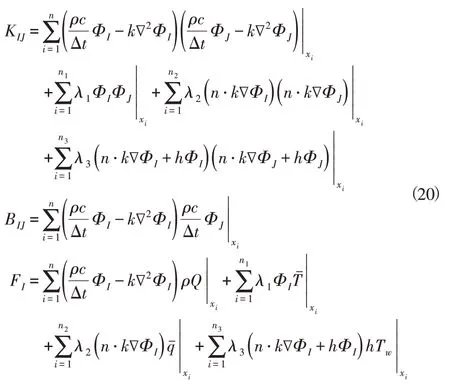
上述计算过程中，将三种边界条件以罚参数的方式引入求解，为了平衡不同约束条件残量的数量级，并且使边界条件的残差相对于控制方程来说在求解中占主导地位，经过量纲分析定义λ1=λ2（k/L）2，λ3=λ2[min（1，k/hL）]2，其中参数λ2推荐值为（105～108）。

3 实例分析及试验验证

3.1 轴承温度场分析

以CNC机床滚珠丝杠进给驱动中预拉伸端轴承25TAC62B（NSK）为研究对象。采用MWLS建立非稳态温度场模型。设置外部环境温度23℃，轴承工作转速1500r/min。滚动轴承的发热大部分来源于滚珠和内外滚道的相互滑动和摩擦，根据文献[10]计算出轴承发热量为Htot=2.79W。由Steph 和Burton 所提出的观点，其轴承运行时产生的热量50%进入滚动体，另50%传入外圈和内圈。25TAC62B 轴承结构参数为：公称外径De=62mm；公称内径Di=25mm；外圈内径de=51.57mm；内圈外径di=37.37mm；滚动体直径D=6.9mm；内沟道沟半径ri=3.65mm；外滚到沟半径re=3.65mm；滚动体数目Z=18；接触角α=60°。

由于轴承外圈外表面与轴承座内表面紧密连接，忽略其接触热阻，所以将研究对象简化为三个部分，分别为轴承内圈、球和轴承外圈加轴承座，如图1所示。

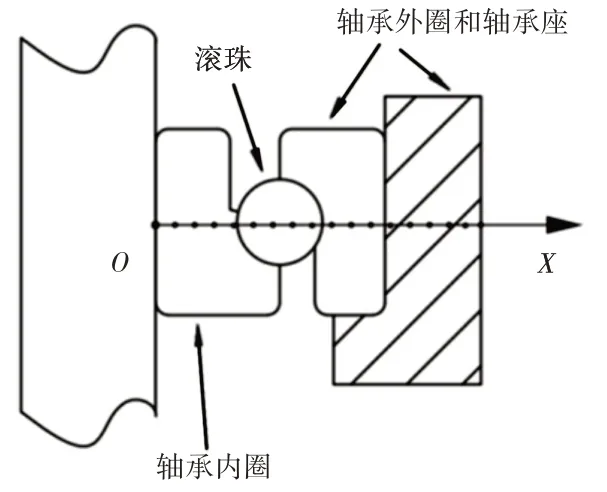
图1 轴承节点分布简图Fig.1 Schematic Diagram of Bearing Node Distribution

对轴承内圈进行分析，其受到轴承摩擦热和轴端散热影响，内圈沟道为该部分摩擦热的影响面，经过计算内圈沟道面积s1=711.93mm2。沿图1中x轴方向均匀分布8个计算节点，得到内圈沟道温度随时间变化曲线，如图2所示。得到各节点在不同时刻温度场分布，如图3所示。

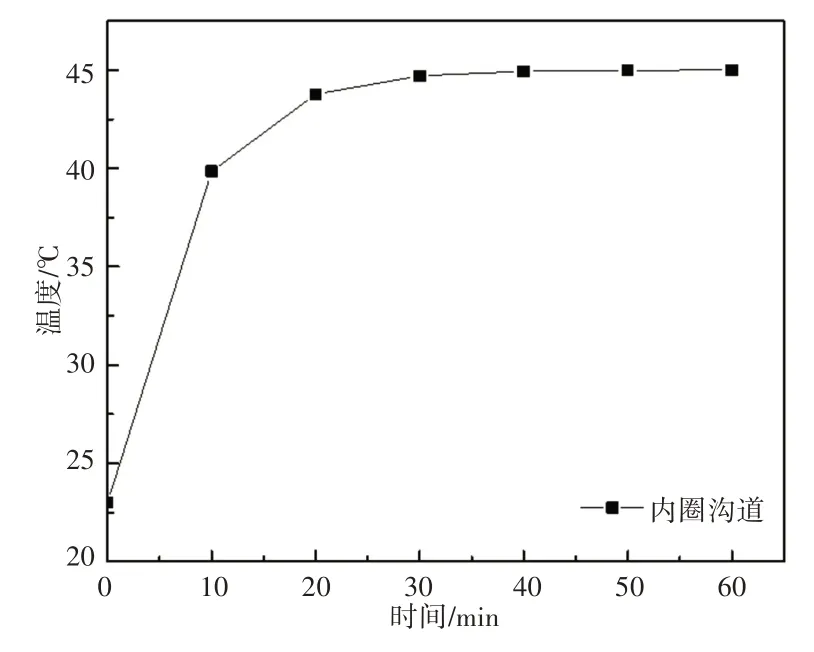
图2 轴承内圈沟道温度随时间变化图Fig.2 Variation of Temperature of Bearing Inner Ring Groove with Time

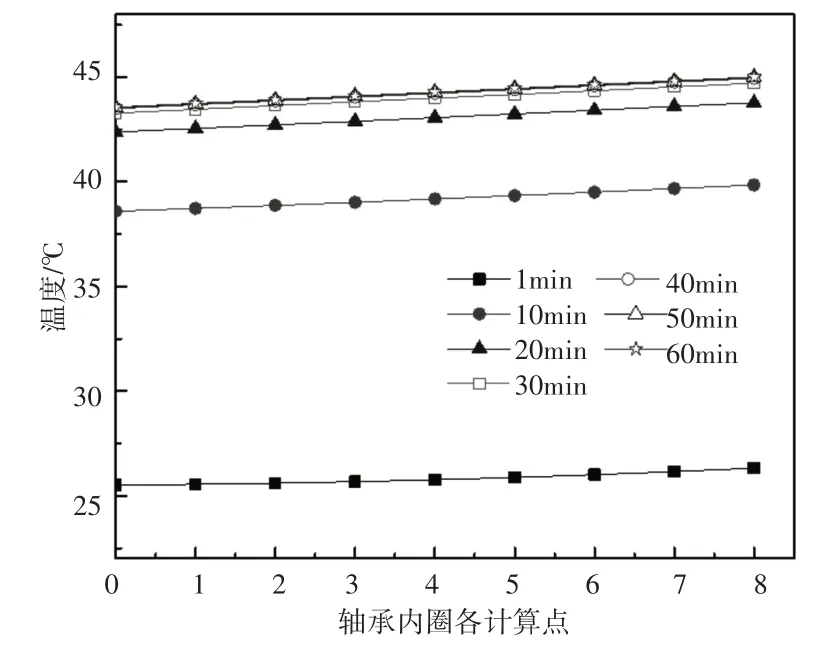
图3 轴承内圈各计算点在不同时刻温度变化图Fig.3 Temperature Variation Diagram of Each Calculation Point of Bearing Inner Ring at Different Time

计算结果表明轴承内圈温度在运行初期温升较大，在35min附近接近稳态，最终达到稳态温度为45.03℃。由于轴承内圈较小，轴端散热率低，各个计算点温度趋于一致比较容易，所以在同一时间各节点间温差较小。对滚珠进行分析，滚珠受到两端轴承摩擦热和润滑油持续散热影响，将滚珠影响面简化为滚珠的一半表面，经计算s2=s3=172.93mm2。将润滑油造成的球表面散热转化为随各点温度变化的负的内热源。经计算得滚动体中心点温度随时间增长曲线，如图4所示。其在35min左右达到38.04℃后趋于稳定。沿图1中x轴所示方向均匀分布14个计算节点，得到各节点在不同时间下的温度分布规律，如图5所示。

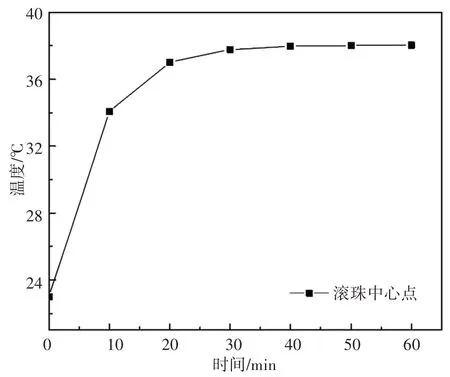
图4 滚珠中心点温度随时间变化示意图Fig.4 Temperature Changes of Ball Center Point with Time

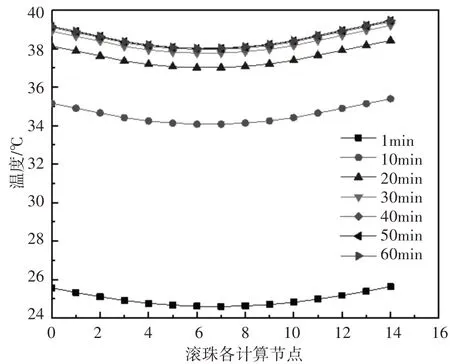
图5 滚珠各计算点在不同时刻温度变化图Fig.5 Temperature Variation Diagram of Each Calculation Point of the Ball at Different Moments

对轴承外圈及轴承座部分进行计算，该整体主要受到轴承摩擦生热和轴承座对流散热的影响，外圈滚道为该部分摩擦热的影响面，经过计算外圈滚道面积s4=1187.06mm2，对整个研究对象均匀划分18个计算节点，得到轴承外圈滚道和轴承座表面温度随时间变化规律，如图6所示。以及不同时间轴承温度场分布状况，如图7所示。结果表明外圈沟道和轴承座在35min后温度分别在29.51℃和27.5℃达到稳态。

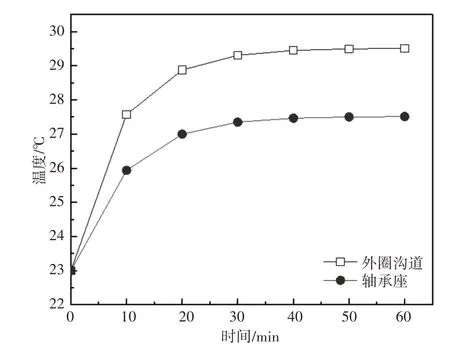
图6 轴承外圈沟道与轴承座温度随时间变化图Fig.6 Variation of the Temperature of Outer Ring Channel and Bearing Seat with Time

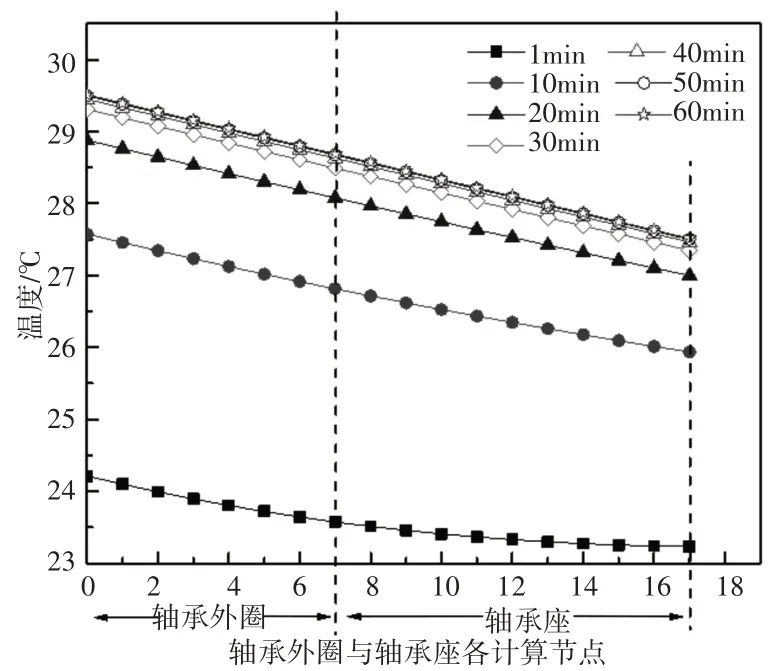
图7 轴承外圈与轴承座各计算点在不同时刻温度变化图Fig.7 Temperature Changes of the Calculated Points of the Bearing Outer Ring and Bearing Seat at Different Times

3.2 试验验证

该试验由滚珠丝杠驱动系统和精度为0.1℃的FLUKE热成像设备组成，实验装置，如图8所示。将拉伸端轴承作为测试对象，测点位置为轴承座外顶面中点。该轴承材料的物理特性参数为，密度ρ=7800kg/m3；比热容c=460J/kg·K；材料导热系数k=39W/（m·K）。其中机床滚珠丝杠驱动系统的丝杠工作转速为1500r/min。

图8 实验装置Fig.8 Experimental Device

测试时，首先测量试验的环境温度等于23.0℃，电机开机并以转速为1500r/min驱动丝杠暖机，试验时间累计为1h，采用热成像仪对温度测点时间间隔10min采样一次，采样热成像图以及测点位置示意，如图9所示。最后使用SmartView读取并保存的测试结果。

图9 热成像图及测点位置Fig.9 Heat Image and Position of Measuring Point

将轴承座计算结果与试验数据汇总，如图10所示。经对比验证可得该温度辨识结果与试验结果均呈指数上升趋势，趋势合理。轴承座外圈计算温度与试验温度最大差值为0.637℃，其最大误差为2.46%。

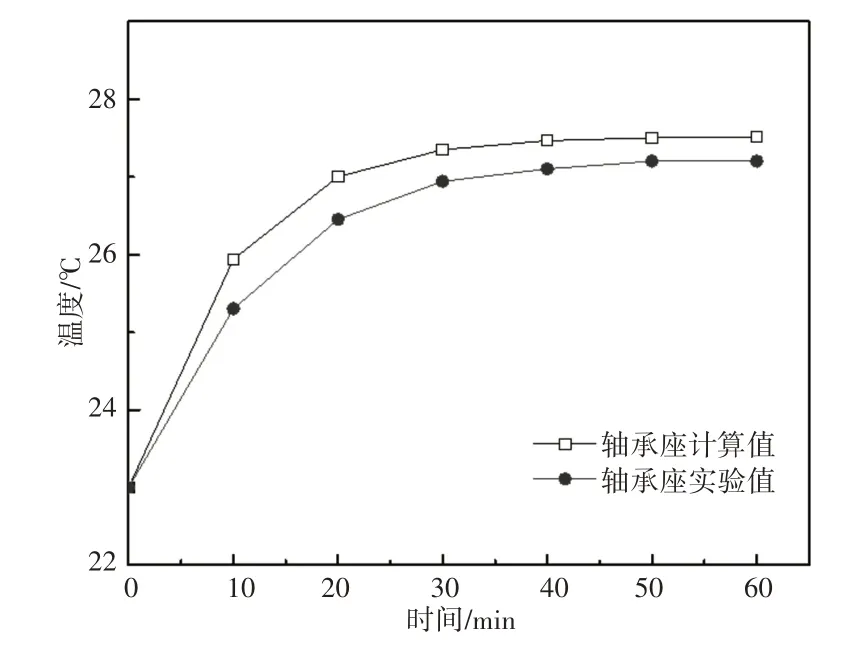
图10 轴承座温度实验值和计算值对比Fig.10 Comparison of Experimental and Calculated Values of the Bearing Seat Temperature

4 结论

提出了基于无网格传热的轴承温度场建模方法，得到了一般工况下轴承各元件的瞬态温度场。该计算方法获得了轴承各部分沿径向温度分布规律，由于不需进行网格的划分，并且该方法所得到的温度刚度矩阵为带状矩阵，计算规模减少，计算速度提高明显，并且与实验结果进行对比，证明该模型是一种快速准确的计算轴承瞬态温度场的数值方法。