内置圆柱对台阶绕流流动及传热特征的影响

谢纬安，彭婧华，喜冠南

（1.南通职业大学汽车与交通工程学院，江苏 南通 226007；2.南通大学机械工程学院，江苏 南通 226019）

1 引言

台阶绕流与钝体绕流都是经典的绕流模型，这两类绕流在工程中也都有着广泛的应用，如建筑、桥梁、车身、飞机周围的流动等。在后向台阶流道中内置圆柱后所引发的绕流兼具台阶绕流和钝体绕流的特征，其独特的局部流动传热特征具有广阔的应用前景。

对于单一的后向台阶绕流与圆柱绕流，已有不少文献研究了其流动传热机理[1-4]。对于后向台阶内置圆柱绕流，现有的研究相对较少，文献[5]研究了低雷诺数Re≤200时内插固定圆柱对后向台阶绕流传热特性的影响，结果表明内插固定圆柱可使底面努塞尔数峰值最大提高155%，但整个台阶底面平均努塞尔数略有下降。文献[6]模拟了层流时，进口脉动来流、内插固定圆柱条件下的后向台阶绕流。结果表明传热性能随脉动频率和纳米粒子体积浓度的增大而增强。他们还研究了插入旋转圆柱对后向台阶绕流中纳米流体流动传热特性的影响[7-8]。

在层流强制对流时，旋转圆柱能够有效改变主回流区形态，且在低雷诺数时对提升局部努塞尔数更有效；在层流混合对流时，传热随着雷诺数及纳米粒子体积浓度的增长呈线性上升，圆柱的旋转速度为Ω=-4.5和Ω=1.5时能有效强化传热。

除内置圆柱之外，文献[9]也研究了内置方柱对脉动来流的控制作用，具体分析了方柱在两种不同位置时对局部传热的影响，最大传热提升分别为228%和197%。文献[10]对后向台阶内插方柱绕流进行了模拟研究，分析了方柱插入位置的流动形态以及局部传热变化，结果表明局部传热最大可提升193%。

从现有的后向台阶内置圆柱绕流研究来看，内置圆柱在主回流区分离剪切层不同位置对流动传热影响的研究尚不全面，圆柱直径大小对下游流动形态及局部传热特影响的研究很少，圆柱绕流与台阶绕流复合作用下的强化传热机理也未完全阐明。因此，针对以上存在的研究不足，通过Fluent进行数值模拟，来研究后向台阶内置圆柱绕流的流动传热特性，重点分析宽范围圆柱流向插入位置以及圆柱直径这两个因素的作用，并结合这两方面的影响找出最佳的流动传热工况。

2 研究方法

2.1 物理模型及边界条件

为了研究后向台阶内置圆柱绕流的流动传热，建立了的物理模型，如图1所示。图中：S—台阶高度（特征长度）；L0—台阶上游壁面长度；L1—底面长度；H—出口高度；Xc—圆柱圆心到台阶垂直面的距离；Yc—圆柱圆心到底面的垂直距离；D—圆柱直径，。物理模型中各参数取值为：S=0.015m，H=0.03m，L0=0.015m，L1=0.9m，D=0.006m，流道扩张比ER=H/h=2，流体计算区域为图示灰色区域，该物理模型的边界条件表达如下。

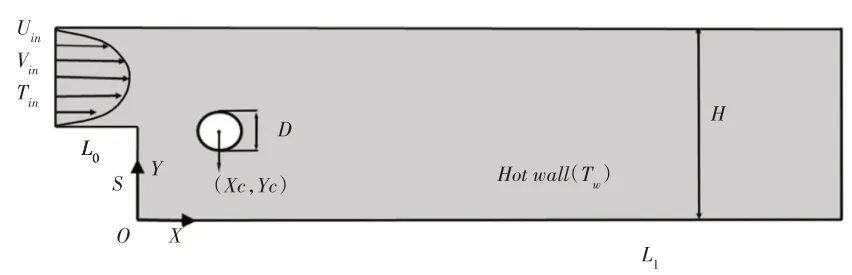
图1 计算模型示意图Fig.1 Schematic of the Computational Domain

进口边界：进口X方向速度u的定义采用UDF程序导入，满足充分发展条件，呈抛物线分布；Y方向速度v为0，流体温度均匀分布T0=293K。

出口边界：出口处流动充分发展，X方向的压力为变量，其余参数在出口处的梯度变化为0。

壁面边界：所有壁面边界无滑移，除台阶底面外均为绝热壁面，底面等温加热Tw=294K，△t=Tw-T0=1K，可以忽略粘性耗散以及温度引起的热浮力效应对流动传热的影响。

2.2 控制方程及求解

数值模拟研究做出了以下假设：流体为不可压缩牛顿流体，流动为二维流动，流体的物性值为常量。控制方程表达如下：

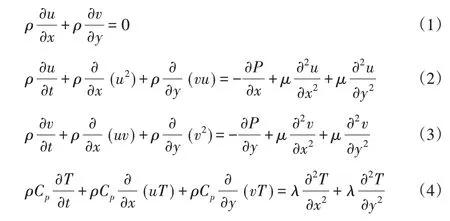
式中：u—流向速度；v—法向速度；Cp—定压比热容；P—压力；T—温度；ρ—密度；m—动力粘度；λ—导热系数。

参数取值为：ρ=1.247kg·m-3；μ=1.76×10-5kg·m-1·s-1；λ=0.0251W·m-1·K-1；Cp=1.005kJ·kg-1·K-1。

基于以上控制方程，在Fluent中采用有限容积法对该模型求解。对流项采用QUICK格式进行离散，扩散项采用中心差分格式离散，ADI算法用来求解全隐式的差分方程。求解过程中进行反复的迭代，并采用SIMPLE算法进行速度压力耦合修正。

2.3 网格划分及实验验证

采用非均匀网格划分计算区域，对圆柱周围进行加密以满足计算要求，如图2所示。为了验证网格独立性，定义基于最小网格宽度的网格雷诺数Reg（Reg=ρu0△xmin/μ），对同一工况表1中三种不同的网格精度（Reg=16、8、4）进行网格独立性验证。通过比较发现，在Reg=8时计算结果已经能够满足计算准确性要求。因此，从计算时间和计算精度两方面考虑，选取Reg=8进行计算，此时网格数为152898。

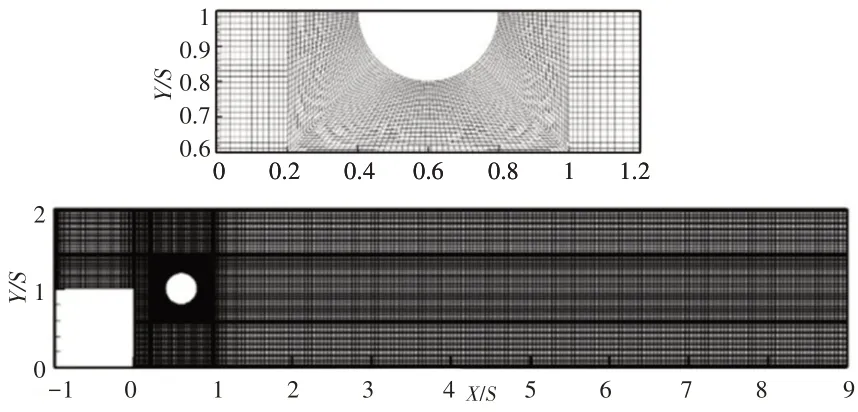
图2 网格系统示意图及局部放大图果Fig.2 Schematic of the Grid System and Local Enlarged View

表1 不同网格精度对比Tab.1 Comparison Diagram of Different Grids

在验证了网格独立性后，采用PIV实验对数值模拟的准确性进行进一步的验证，实验采用闭式循环水槽实验台。通过水泵实现水流循环，通过调节阀控制水流速度，电磁流量计测量水流量。水流经过多次整流之后进入实验段，表现为充分发展的稳定流场，在实验段进行后向台阶内置圆柱绕流的PIV实验。

配套使用的粒子图像测速系统，如图3 所示。实验时在流场中投放适量的示踪粒子，利用示踪粒子的运动来表征实验区域流体的运动状态。双脉冲激光器的最高频率为100Hz，能够均匀照亮实验区域。示踪粒子为镀银空心玻璃球，表面镀银处理后具有良好的光散特性，镀银空心玻璃球粒径大小约为（0.001～0.0015）mm。

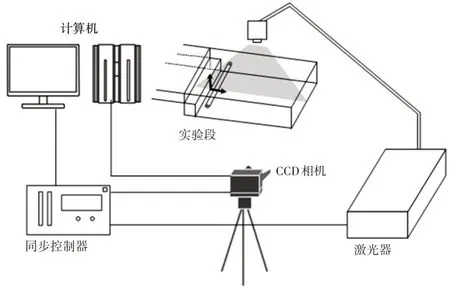
图3 PIV系统的布置Fig.3 Arrangements of PIV System

Re=700 时PIV 实验和数值模拟一个流动周期内不同时刻（分别代表1/4T，1/2T，3/4T，T时刻）的流场，如图4所示。圆柱位置位于Xc/S=0.6，Yc/S=1，实线为流线，箭头为速度矢量。通过对比实验与数值模拟结果，在一个流动周期内随着时间的推移，整体旋涡结构、旋涡数量及尺度、旋涡运动演变特征均相似度高。因此，可认为数值模拟结果有较好的准确性。此外，由于实验存在不可避免的误差，结果存在一定的偏差属正常现象。

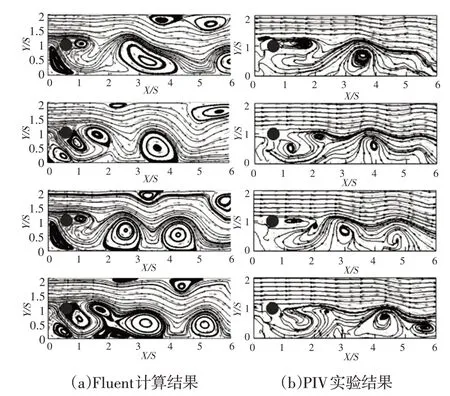
图4 一个周期内不同时刻的瞬时流场图Fig.4 Instantaneous Flow Fields for Various Time Instants in a Periodic Cycle

3 结果与讨论

3.1 圆柱位置对流动传热的影响

为了考察圆柱在不同流向位置时对主回流区以及下游流动形态的影响，Re=500时圆柱在不同插入位置的瞬时流线及速度场，如图5所示。

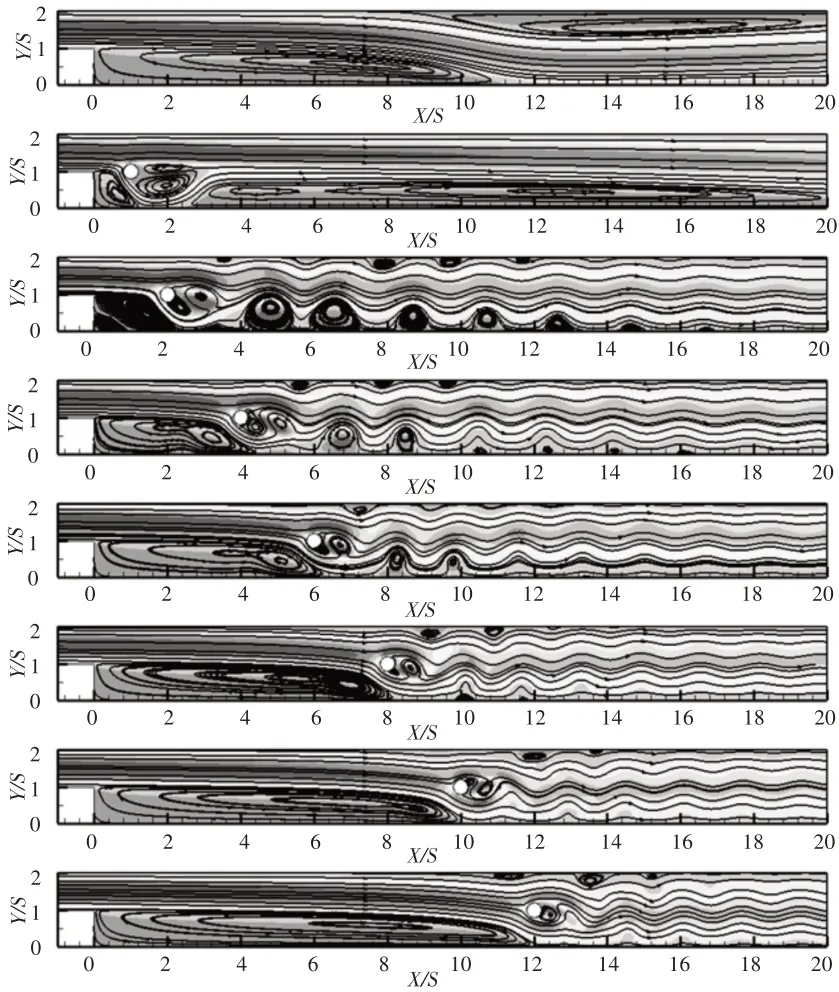
图5 不同内置圆柱位置时的瞬时流场图Fig.5 Instantaneous Flow Fields for Different Streamwise Position of the Insert Cylinder

图中在无圆柱工况下，Re=500时的台阶绕流表现出层流流动特征，形成了单个大尺度旋涡的主回流区与二次回流区，下游流动稳定。在内置圆柱后，流道中的流动形态出现了不同程度的变化。当圆柱的流向插入位置小于主回流区再附着长度时，都能够对主回流区的发展起到抑制的作用。

其中Xc/S=1时主回流区受到圆柱分离剪切层的破坏，但未能在下游引起明显的流动不稳定性，而是在圆柱下游诱导形成了一个大尺度回流区，流向尺寸从X/S=3延伸至X/S=20。当10≥Xc/S≥2时，圆柱抑制主回流区发展的同时，在下游引起了具有复合绕流特征的旋涡，包含了圆柱后方的旋涡对以及台阶底面上方的近壁旋涡。随着Xc/S的增大，圆柱后方的旋涡变化不大，台阶底面上方旋涡的尺度减小，数量减少。当Xc/S=12时，内置圆柱不再对主回流区形成抑制，但同样引发了下游流道中的流动不稳定性。在所有内置圆柱的工况下，单个旋涡的顶面回流区均消失，多数工况下演变为顶面附近的若干小尺度旋涡。

Re=500时圆柱在不同插入位置的瞬时温度场，如图6所示。图中无内置圆柱的工况时，温度场分布均匀，高温流体聚集在主回流区内，下游流体温度未产生波动。内置圆柱后，在Xc/S=1时，温度场的分布相对比较特殊，内置圆柱在破坏局部温度分布后，流体温度在圆柱下游很快恢复均匀分布。当10≥Xc/S≥2时，内置圆柱在破坏主回流区温度分布的同时，引起了再附着点下游较为明显的温度波动，且温度波动的幅度随Xc/S的增大先增大后减小，在Xc/S=8时温度波动幅度达到最强。内置圆柱引起的流体提前再附着对局部温度边界层有显著的破坏作用，尤其是Xc/S=1和Xc/S=2这两个工况。

图6 不同内置圆柱位置时的瞬时温度场图Fig.6 Instantaneous Temperature Fields for Different Streamwise Position of the Insert Cylinder

Re=500时圆柱在不同插入位置台阶底面的时间平均努塞尔数和时间平均摩擦系数曲线，如图7所示。

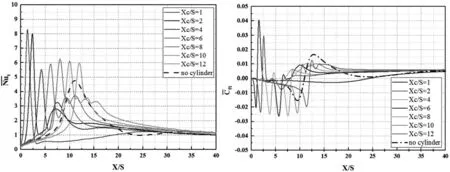
图7 不同内置圆柱位置时的底面时均努塞尔数与摩擦系数Fig.7 Time-Mean Nusselt Number and Skin Friction Coefficient Distributions of Bottom Wall for Different Streamwise Position of the Insert Cylinder

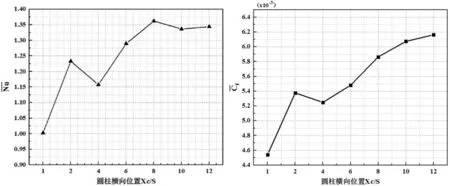
图8 不同内置圆柱位置时的时空平均努塞尔数与摩擦系数Fig.8 Time and Space Mean Nusselt Number and Skin Friction Coefficient for Different Streamwise Position of the Insert Cylinder

3.2 圆柱直径对流动传热的影响

阐明了内置圆柱的最佳流向插入位置为Xc/S=8的基础上，进一步考察圆柱大小对流动传热特性的影响。Re=500不同内置圆柱直径时的瞬时流线及流向速度场，如图9所示。

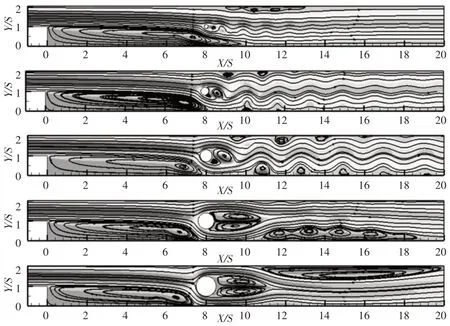
图9 不同圆柱直径时的瞬时流场图Fig.9 Instantaneous Flow Fields for Different Diameter of the Insert Cylinder

从图9中可以看出，圆柱直径对主回流区的影响不大，对圆柱尾流以及下游的流动形态影响明显。随着圆柱直径D的增大，主回流区再附着点位置逐渐向上游移动，圆柱后方的旋涡尺度不断增大，流道下游的流动不稳定性先增强后减弱。

当D=0.2S时，主回流区在圆柱插入位置向下游有一定延伸，其再附着位置在圆柱插入位置的下游，同时下游的流体波动幅度较小，壁面附近未形成明显的旋涡。当D=0.4S时，主回流区的发展不再向下游延伸，在圆柱插入位置附近形成再附着，下游流体的波动幅度增强。当D=0.6S时，流动形态的变化主要在于下游流道壁面附近交替形成的旋涡以及主流波动的进一步增强。当D=0.8S时，流道的阻塞比增大，流体在掠过圆柱时加速效应显著。

下游主流的波动减弱，底面附近由多个未分离的旋涡连接形成较大尺度的回流区。当D=S时，流体加速效应进一步增强，下游形成由单个回流涡构成的大尺度顶面二次回流区，底面附近的流动平稳。Re=500不同内置圆柱直径时的瞬时温度场，如图10所示。

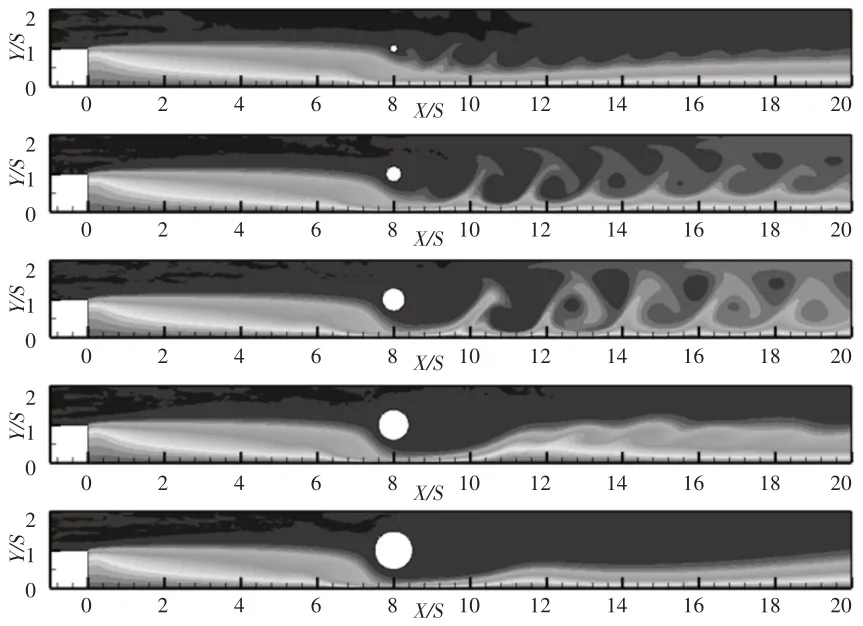
图10 不同圆柱直径时的瞬时温度场图Fig.10 Instantaneous Temperature Fields for Different Diameter of the Insert Cylinder

圆柱直径对下游温度场形态的影响显著。圆柱插入位置附近壁面的温度边界层厚度随D的增大而减小，下游传热不稳定性随D的增大先增大后减小。在D=0.4S和D=0.6S时，下游的温度场出现较大幅度的波动，主流内的低温流体与壁面附近的高温流体充分换热。在D≥0.8S后，下游的温度场波动逐渐减弱，在D=S时下游的温度边界层恢复为层流温度边界特征。

Re=500 时圆柱不同直径台阶底面的时间平均努塞尔数和时间平均摩擦系数曲线，如图11所示。

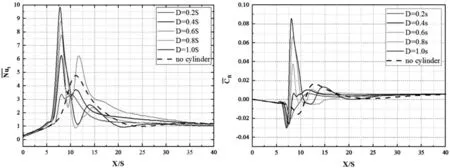
图11 不同圆柱直径时的底面时均努塞尔数与摩擦系数Fig.11 Time-Mean Nusselt Number and Skin Friction Coefficient Dis⁃tributions of Bottom Wall for Different Diameter of the Insert Cylinder

Re=500时圆柱不同直径台阶底面的时间空间平均努塞尔数和时间空间平均摩擦系数，如图12所示。

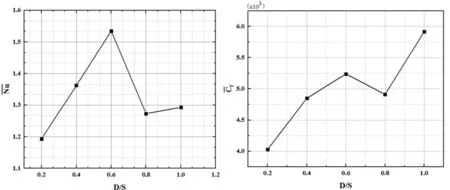
图12 不同圆柱直径时的时空平均努塞尔数与摩擦系数Fig.12 Time and Space Mean Nusselt Number and Skin Friction Coefficient for Different Diameter of the Insert Cylinder

4 结论

通过研究内置圆柱对后向台阶绕流流动形态及强化传热的影响，主要的到了以下结论：

（1）内置圆柱对后向台阶绕流的影响主要包括了两方面，一方面是抑制主回流区分离剪切层的发展，进而破坏主回流区的流动形态；另一方面是圆柱尾流与再附着流体共同引发复合流动不稳定性，在下游流道壁面附近诱导出交替变化的旋涡。

（2）内置圆柱的流向插入位置主要影响主回流区形态与下游流动不稳定性。对于主回流区形态，在流向插入位置小于主回流区流向尺度时，内置圆柱能够破坏台阶绕流分离剪切层的发展，提前引起流体再附着，促使壁面的局部传热明显增强。对于下游流动不稳定性，除Xc/S=1 时其它工况在内置圆柱后均能够引起下游的流动不稳定性，对壁面传热起到不同程度的强化作用。

（3）内置圆柱的直径主要影响圆柱周围的流体加速效应和下游流动形态。随着圆柱直径的增大，圆柱绕流分离剪切层的流速逐渐增大，圆柱附近壁面的传热逐渐增强，圆柱下游的流动不稳定性先增强后减弱。

（4）综合内置圆柱流向插入位置与圆柱直径来看，在所研究的工况中，Xc/S=1、D=0.6S时内置圆柱后向台阶绕流表现出了最佳的流动传热特性。