电动主动横向稳定杆的模型预测控制研究

张勇超，喻 凡，王立标

（1.台州学院智能制造学院，浙江 台州 318000；2.上海交通大学机械系统与振动国家重点实验室，上海 200240）

1 引言

当前，汽车交通事故是社会安全方面的严重问题之一。美国国家公路交通安全管理局的年报数据显示[1]，从1982年到2017年，在美国所有汽车事故中，侧翻事故仅占2%左右，而乘用车和轻型卡车翻车事故造成的死亡人数达到总死亡人数的31%，翻车事故是最致命的交通事故之一。因此，提高车辆的侧倾稳定性来减少翻车事故的发生是非常必要的。被动横向稳定杆是最经济的稳定车身侧倾姿态的方法，已被工业界广泛认可，但其缺点也很明显，即悬架的侧倾刚度不能随车辆行驶工况的变化自适应调节。近二十年来，主动横向稳定杆受到工业界和学术界的关注。主动横向稳定杆可以在汽车转弯和行驶在不平路面时，产生主动防侧倾力矩，降低车身侧倾角，有效提高车轮与道路的附着条件，从而获得良好的行驶稳定性和乘坐舒适性。根据力矩作动器形式的不同，乘用车主动横向稳定杆有两种类型。一种是气液或液压系统[2-3]，这是车辆主动横向稳定杆最常用的作动器形式。宝马公司于2001年开发了Dynamic Drive主动防倾杆系统[4]。该系统已应用于宝马5系、6系和7系车型上，在小侧向加速度工况下，车身侧倾角趋近于0，但缺点也比较明显，即成本高，功耗较高。另一种是利用电机作动器的电磁系统[5-6]，相比于液压系统，它的能量效率更高，响应速度更快。丰田公司首先将直流无刷电机应用到主动横向稳定杆上，并配备在LEXUS的GS车型上[7]。某公司也开发出基于直流电机的主动侧倾控制系统[8]，并装备到宝马7系和宾利添越等高端车型上。随着电动汽车的快速发展，人们对汽车安全性和舒适性提出了更高要求，电机式主动横向稳定杆正好契合了这些要求，具有较好的发展潜力。

国内外学术界针对电动主动横向稳定杆做了许多研究。在抗侧倾控制方法上，PID控制、模糊控制、最优控制、滑模控制、鲁棒控制等成熟控制算法都取得了研究成果，控制器设计思路都是根据侧向加速度信息结合侧倾角的变化来计算防侧倾力矩，控制器设计内容主要有以下几方面：

（1）悬架与转向系统的集成控制。将侧倾运动与横摆运动进行协调控制，利用侧向加速度信息通过PID控制器[9]、前馈和反馈控制器[10]、backstepping非线性控制器[11]来计算防侧倾力矩，再利用模糊PID控制器合理分配前后主动防侧倾力矩[10-11]；

（2）针对典型类型的主动横向稳定杆设计防侧倾控制器。比如，针对不考虑结构和力学特点的理想主动横向稳定杆，设计PID控制器[12]、模糊滑模控制器[13]，实现对车身侧倾角的理想跟踪控制；针对液压式主动稳定杆具有非线性特性，建立非线性动力学模型，并设计相应的控制器，比如滑模控制器[14]、LQR 控制器[15]、LQG控制器[16]、H∞控制器[17]，实现车身侧倾角的最优控制；针对电机式主动横向稳定杆系统，采用双闭环控制算法，外环控制器跟踪控制车身侧倾角，比如PID控制器[18]、滑模控制器[19]等，内环控制器跟踪控制电机的输出扭矩；

（3）重要参数估计。侧向加速度、车身侧倾角是防侧倾控制中重要依据参数，可以采用卡尔曼滤波算法[16]、无迹卡尔曼滤波算法[20]等算法在线估计，也可以通过车-车通信方式，利用预瞄方法将前车参数传送过来[21-22]。

国内外工业界和学术界已经积累了许多汽车抗侧倾控制的开发和研究成果，但针对以开关磁阻电机（Switched Reluctance Motor，SRM）和谐波减速器组成的电机式主动横向稳定杆作动器的控制研究较少[23]。本研究以此类型的主动横向稳定杆作动器样机作为研究对象，采用Maxwell/RMxprt软件对开关磁阻电机进行电磁场有限元分析，获得精确的SRM电机磁化特性数据，利用这些数据在Simulink 中建立SRM 的特定模型，此电机模型用于电机输出力矩的跟踪控制。基于整车侧倾动力学模型设计MPC控制器，研究主动横向稳定杆的防侧倾力矩对整车动力学性能的影响，通过Simulink和Carsim的联合仿真探究控制器参数对控制性能的影响，验证控制器的有效性。

2 电机作动器特性

电机式主动横向稳定杆作动器由SRM、谐波减速器和稳定杆（扭杆弹簧）组成，作动器结构和样机，如图1所示。SRM采用外定子和内转子结构。SRM的转子连接到谐波减速器的波发生器、带动柔轮、驱动刚轮和稳定杆转动。SRM用于动力输出，谐波减速器用于减速增扭，减速比最高可达到200：1。电机作动器的优势在于输出扭矩大，响应快，结构简单，适合主动侧倾控制。安装在试验台架上的电机作动器样机，如图2所示。

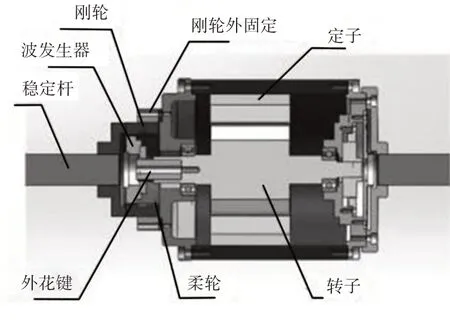
图1 电机作动器结构Fig.1 Structure of Motor Actuator

图2 电机作动器样机Fig.2 Motor Actuator Prototype

SRM的双凸极铁心结构，其铁心磁通密度的高饱和非线性特性决定了很难用简单的数学解析式模型来描述其特性。通常，采用试验法和有限元仿真法来获得电机磁链非线性特性。前者耗时费力，对测试仪器要求较高；后者省时方便，精确度够用，仿真结果利于被研究者重复验证。因此，利用磁场有限元仿真软件Maxwell/RMxprt来计算SRM的非线性磁链曲线，计算得到8/6极4相SRM的磁链曲线数据[24]，如图3所示。

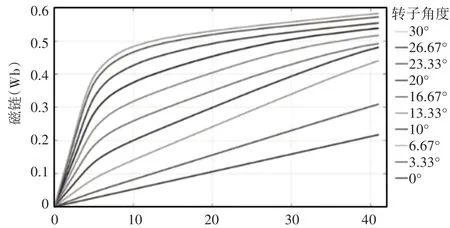
图3 SRM非线性磁链特性曲线Fig.3 Nonlinear Flux Linkage Characteristic Curves of SRM

图中曲线显示：（1）当转子位置稳定，定子线圈电流增大时，磁链增大；当电流增大到一定程度时，磁链缓慢增大，最终趋近饱和；（2）当线圈电流为一定时，转子转动，即转子角度增大（转子凸极对称轴与两个定子凸极之间的中心线重合时，转子角度定义为0°），磁链增大；当线圈电流增大到较大值时，磁链变化率显著减小，即趋于饱和。基于这些曲线数据，利用Matlab/Simulink建立了精确的SRM数学模型。

3 整车侧倾模型

在车身侧倾时，不考虑车身侧倾中心的横向偏移，建模时将整车分为不发生侧倾的非簧载质量和具有侧倾自由度的簧载质量（车身），将车身水平姿态的前后侧倾中心的连线OfOr作为侧倾轴。设前、后侧倾中心距地面的高度分别为hf、hr，前、后轮的轮距分别为df、dr，车身质心ms到侧倾轴之间的距离为hs，前、后轴与车身质心的垂向距离为lf、lr，轴距l=lf+lr，前、后非簧载质量的质心分别为muf、mur，与侧倾轴的距离分别为huf、hur。整车结构尺寸，如图4所示。

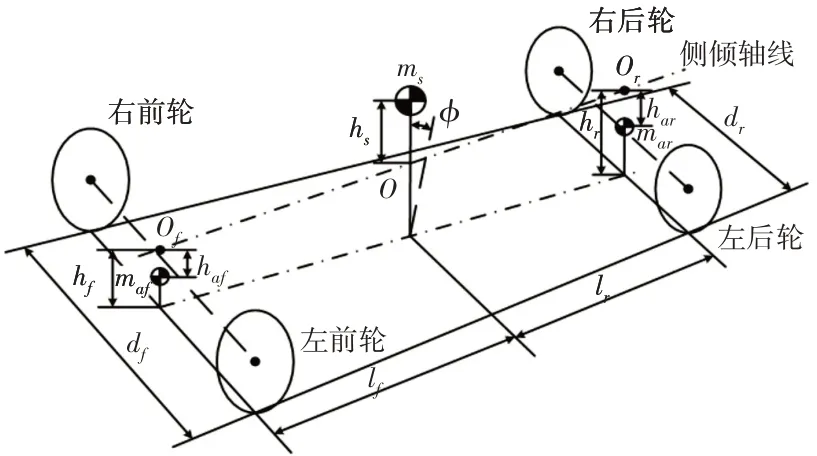
图4 整车结构尺寸Fig.4 Vehicle Structure

假设车身为刚体，忽略轮胎的刚性和阻尼特性，车身在侧向加速度ay的作用下沿着侧倾轴发生侧倾，且侧倾角ϕ很小，车辆的侧倾模型，如图5所示。

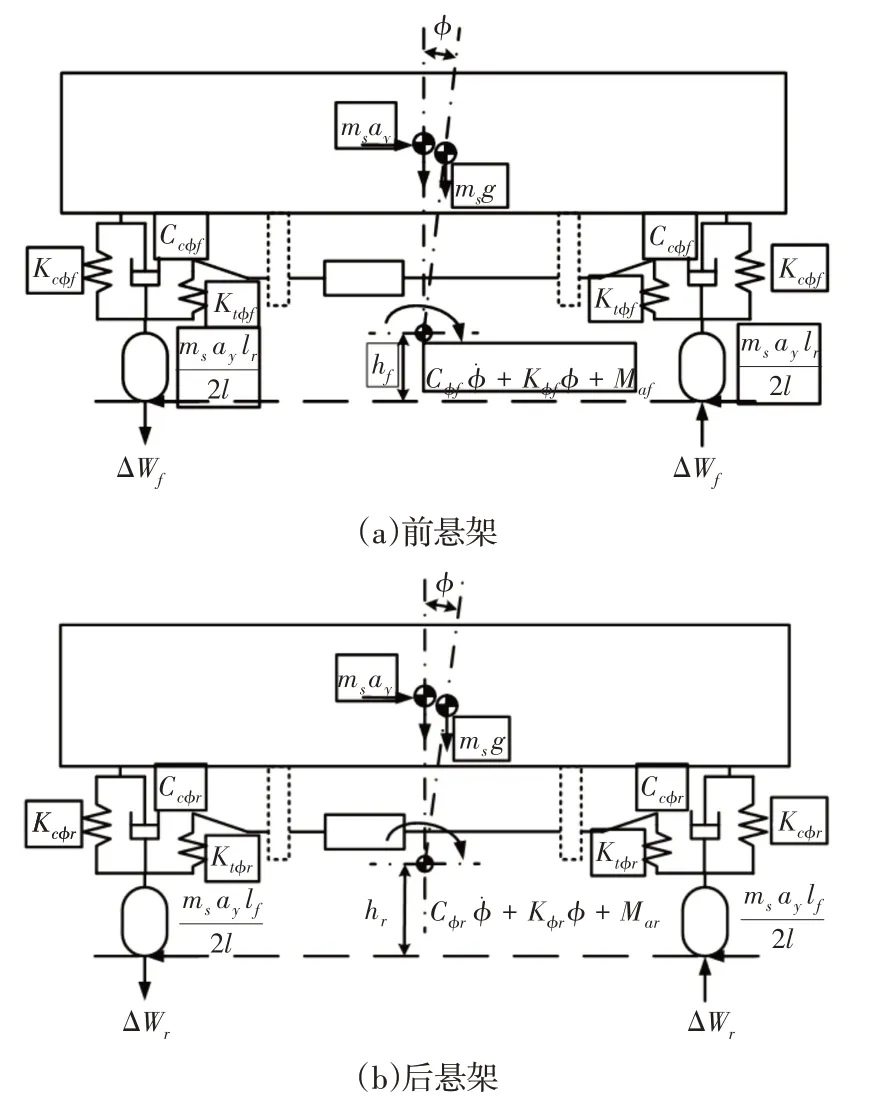
图5 整车侧倾模型Fig.5 Vehicle Roll Model

设前、后悬架的侧倾刚度分别为Kϕf、Kϕr，前、后悬架的弹簧刚度分别为Kcϕf、Kcϕr，前、后稳定杆的扭转弹簧刚度分别为Ktϕf、Ktϕr，前、后悬架阻尼系数分别为Ccϕf、Ccϕr，Ims为车身质量绕侧倾轴的转动惯量，前、后悬架的主动稳定杆电机作动器产生的防侧倾力矩分别为Maf、Mar。

由侧向加速度ay引起的侧倾力矩为msayhs，由车身侧倾产生的侧倾重力矩为msghsϕ，防侧倾力矩由悬架弹簧刚度Kcϕ、主动稳定杆的扭杆弹簧刚度Ktϕ在侧倾角ϕ时产生的力矩以及电机作动器产生的防侧倾力矩Ma组成。侧倾动力学模型如下：

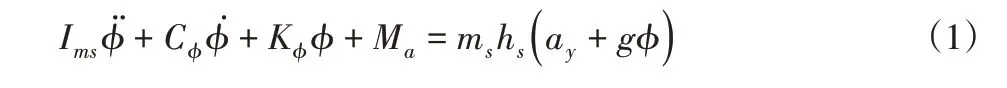
其中，Ims=mshs2；

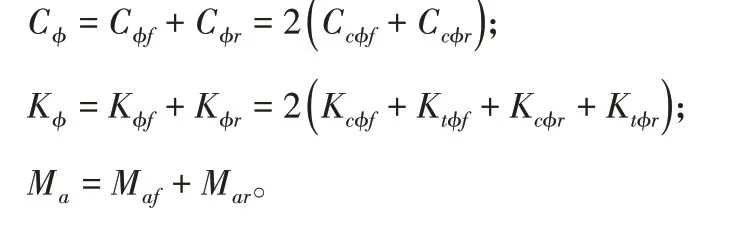
设前后主动稳定杆电机作动器产生的防侧倾力矩分配系数为α，则有：

将式（1）、式（2）联立，可得前主动稳定杆电机作动器产生的防侧倾力矩为：

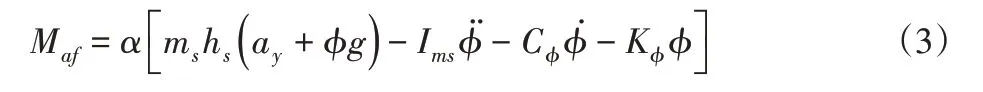
同理，后主动稳定杆电机作动器产生的防侧倾力矩为：

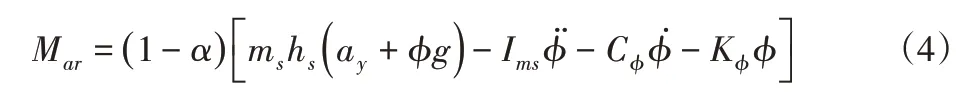
对作用于车辆的惯性力msay而言，必须有与之相平衡的轮胎力。将作用于车身质心的msay分解到前、后轮，则分别有大小为的作用于前、后轮，并分别于前、后轮的侧向力相等。

当车身发生侧倾时，不考虑非簧载质量的侧倾运动，左、右轮的垂向载荷会发生载荷转移，设前、后悬架的载荷转移量分别为ΔWf、ΔWr，以非簧载质量为对象，由绕其相应的侧倾中心的力矩平衡关系可得：

设前后轮垂向载荷转移量分配系数为β，前、后轮胎垂向载荷转移量分别为可得：

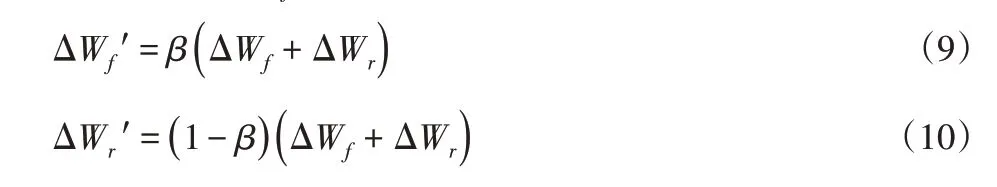
考虑前、后轮垂向载荷转移量的分配，可得需要由电机作动器产生的防侧倾力矩为：

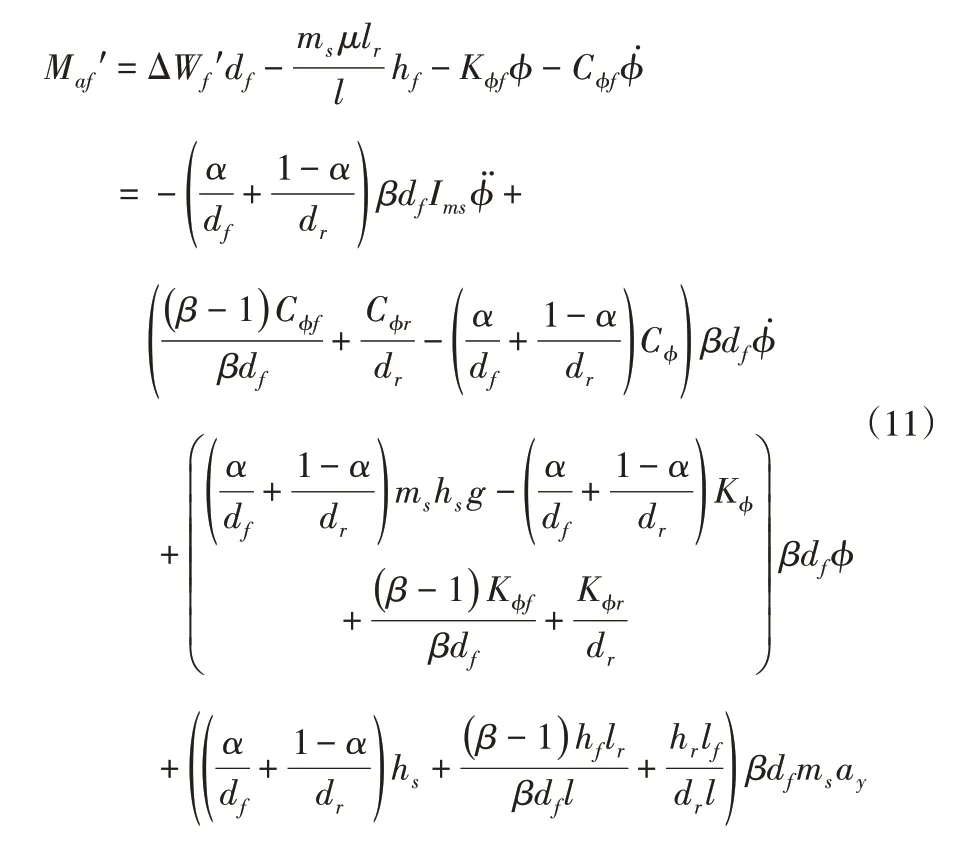
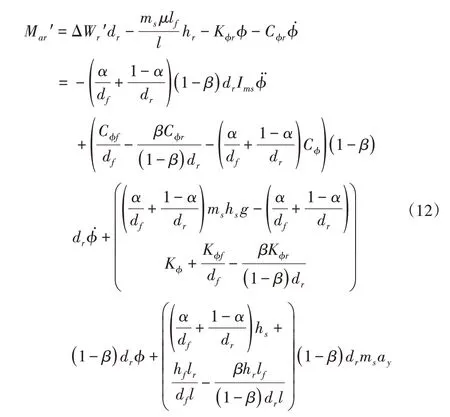
根据横向稳定杆结构尺寸，前、后横向稳定杆电机作动器需要输出的力矩为：

式中：λf、λr—前、后稳定杆纵横比，是与稳定杆几何尺寸有关的常量；daf、dar—前、后稳定杆两端连接孔到稳定杆电机作动器轴线的距离；laf、lar—前、后稳定杆两端连接孔的距离。

结合式（3）～式（14），可得前、后稳定杆电机作动器输出扭矩分别为：

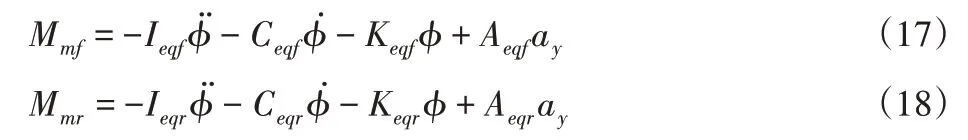
其中，

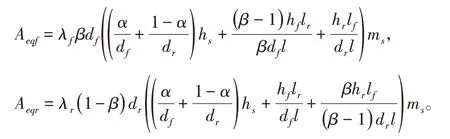
由式（17）和式（18）可以得到前、后主动稳定杆的动力学模型，即：

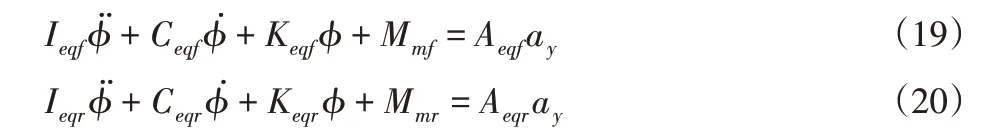
将式（19）化成状态空间形式

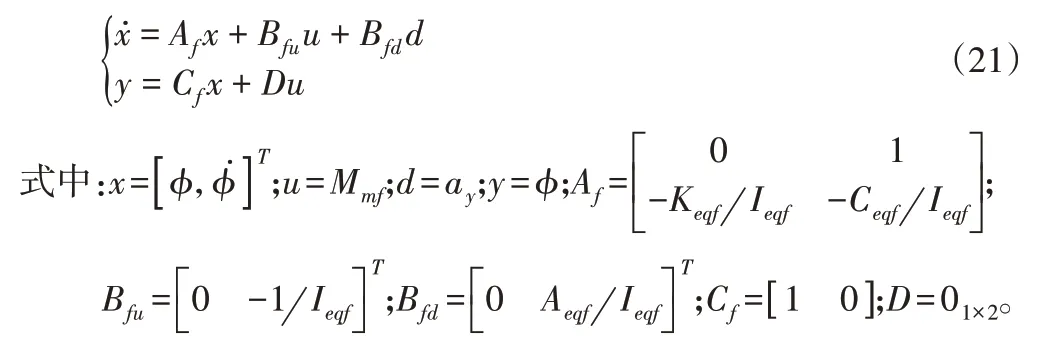
4 MPC控制器

为了给模型设计模型预测控制器，对式（21）进行近似离散化处理：

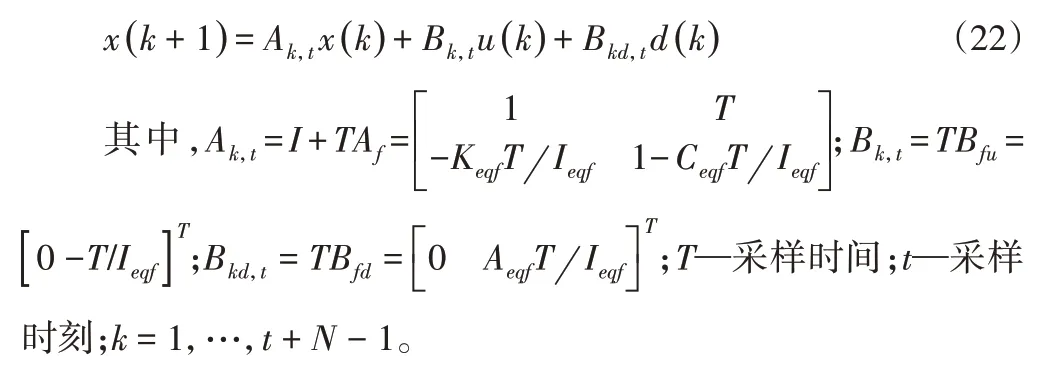
将式（22）进行变换，令：

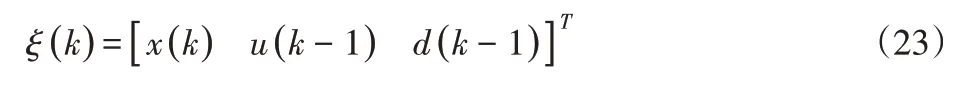
可测干扰d(k)在k时刻之后的预测过程中认为是不变的，即Δd(k)=Δd(k+1)…=Δd(k+Nc)，得到新的状态空间表达式：

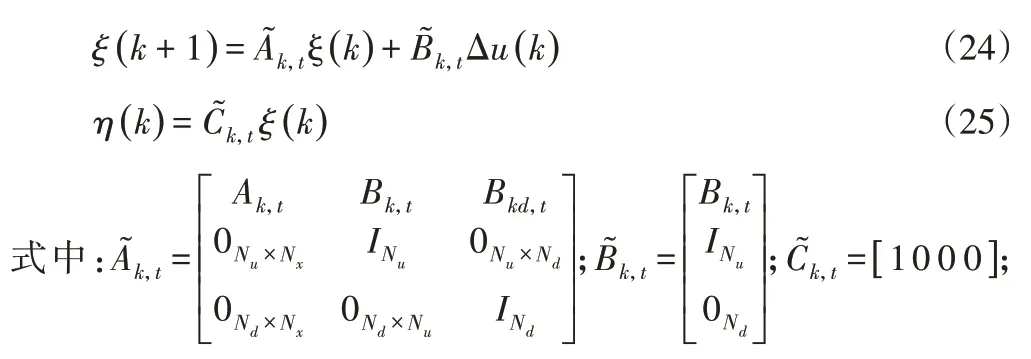
Δu(k)=u(k)-u(k-1)；η(k)—侧倾角ϕ；Nx=4—状态变量维度；Nu=1—控制变量维度。

假设系统参数不变，则：

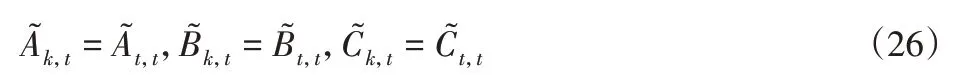
令系统的预测时域为Np，控制时域为Nc，预测时域内的状态变量和输出变量为：

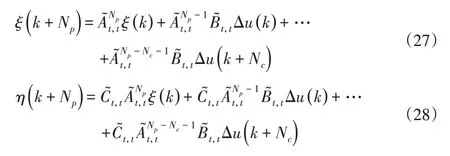
简化系统的预测输出表达式为：

为了能够保证车辆能够快速平稳地追踪期望状态，设计如下形式的目标函数：

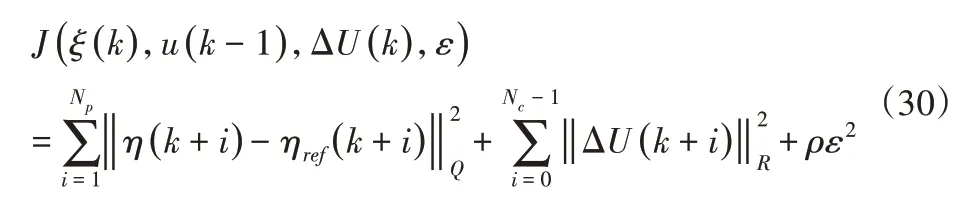
式中：ρ—权重系数；ε—松弛因子。

将式（29）代入式（30），得到完整形式的目标函数：

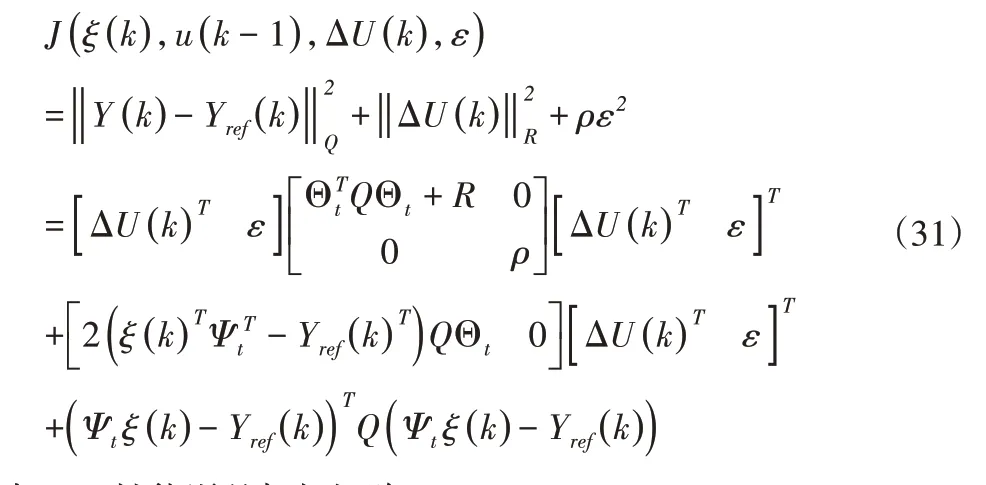
式中：Q—性能误差加权矩阵。

令et=为预测时域内的跟踪误差，它与t时刻获取的状态变量和参考输出变量有关，故为确定值，目标函数可以调整为：

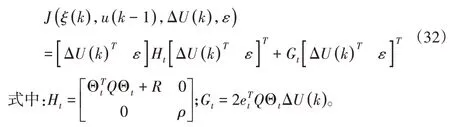
设计目标函数的约束条件如下：

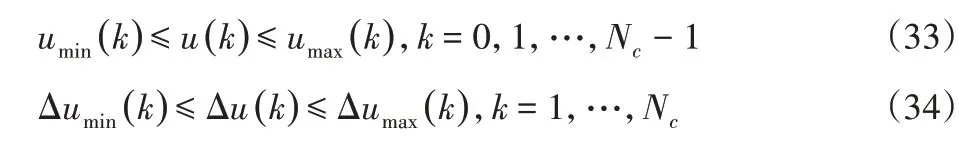
使得目标函数J(ξ(k)，u(k-1)，ΔU(k)，ε)取最小值。

在目标函数中，求解的变量为控制时域Nc内的控制增量，约束条件也只能以控制增量或者是控制增量与变换矩阵相乘的形式出现，故对式（33）进行变换，获得变换矩阵。

式中：u(k-1) —上一时刻实际的控制量。令：

结合式（39）、式（33）和式（34）转换为以下形式：

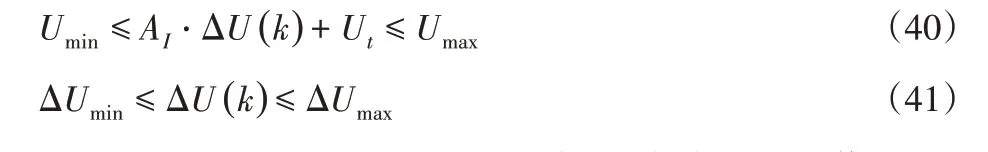
式中：Umin、Umax、ΔUmin、ΔUmax—控制时域内的控制量最小值、最大值、控制增量最小值和最大值集合。

在每个控制周期内完成式（32）的求解后，得到控制时域内的控制输入增量序列：

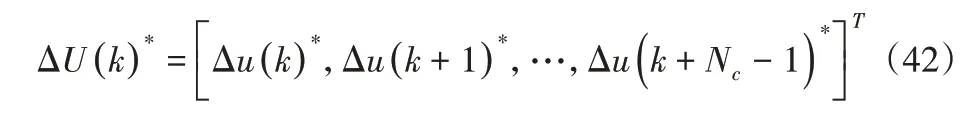
将控制输入增量序列的第一个元素作为实际的控制输入增量作用于系统，即u(k)=u(k-1)+Δu(k)*。进入下一个控制周期后，重复上述过程，循环实现对车辆姿态的跟踪控制。

此模型的输入包含一个可控力矩输入Mmf和一个随机输入ay，后者随着行驶工况和驾驶意图而改变，可以看成是系统扰动输入。由于车辆行驶安全的限制，通常对于轿车的允许侧向加速度取ay∈[-0.8g0.8g]。

车辆转向时，车身随着离心力的作用产生一定的侧倾，过大的侧倾会影响乘适性，并给驾驶员造成心理紧张，严重的侧倾甚至会造成车辆侧翻，因此，合适的车辆理想侧倾角ϕref必须兼顾乘适性和必要的车辆侧倾反馈，使驾驶员对车身姿态有清晰的判断。为了便于计算，令ϕref=0。

后悬架主动横向稳定杆的MPC控制器设计方法与前悬架主动横向稳定杆相同。

5 Simulink与Carsim联合仿真

采用Simulink与Carsim联合仿真来模拟车辆的典型行驶工况，以便验证MPC 控制器的有效性，评估整车动力学性能。在Carsim软件内建立典型的乘用车整车模型，包括转向系统、悬架系统、制动系统、变速箱系统和驾驶员系统等。利用Carsim整车模型快速建立车辆行驶工况，计算得到的车辆数据直接发送到Simlink，作为控制器模型输入，再将控制器输出反馈给Carsim整车模型，从而构建Simulink与Carsim联合仿真平台。联合仿真框图，如图6所示。Simulink整车侧倾模型与Carsim整车模型的车辆参数相同。Carsim整车模型输出包括车辆侧向加速度、车身侧倾角和四轮悬架动行程速度。MPC控制器根据当前的侧向加速度和车身侧倾角计算参考电机力矩。根据四轮悬架动行程速度和车辆悬架尺寸计算出前、后悬架电机转速，联合参考电机力矩，共同作为SRM 作动器模型的输入，计算电机的实际电机输出力矩，最终结合稳定杆尺寸换算成前、后悬架的防侧倾辅助力矩，反馈给Carsim 整车模型，构成联合仿真的闭环控制系统。联合仿真参数[25]，如表1 所示。谐波减速器的减速比设为200：1。为了比较MPC 控制器的性能，还设计了PID 控制器。其输入是侧倾角，输出是防侧倾辅助力矩。比例、积分和微分系数设为kpf=400，kpr=300，kif=100，kir=100，kpf=100，kdr=100，下角标f和r分别代表前、后悬架。

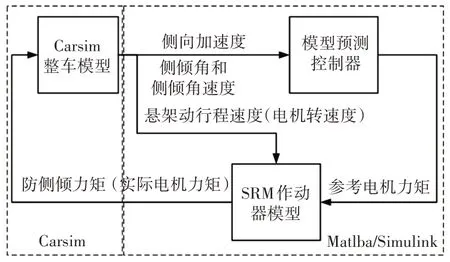
图6 Carsim和Simulink联合仿真框图Fig.6 Co-Simulation Block Diagram of Carsim and Simulink

表1 仿真参数Tab.1 Simulation Parameters

车辆行驶仿真工况设定为车速50km/h的双移线工况。最大侧向偏移为-3.65m，纵向位移限制在60m内，双移线行驶曲线，如图7所示。转向系统采用闭环驾驶员模型。

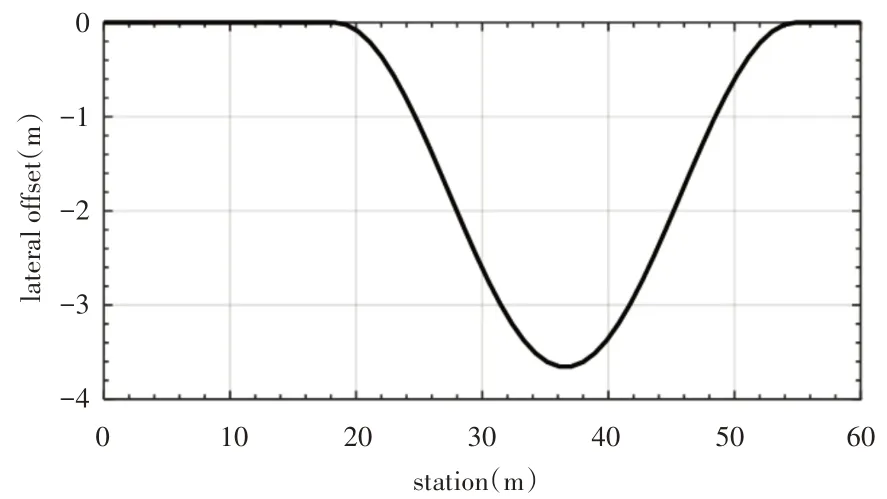
图7 双移线位移曲线Fig.7 Station and Lateral Offset of Double Lane Change

6 仿真结果与分析

配备三种防侧倾系统的车辆在双移线行驶工况下产生了相同的侧向加速度，如图8所示。即仿真试验条件相同，最大侧向加速度为0.8g，达到了正常情况下车辆转向时能够承受的极限值。

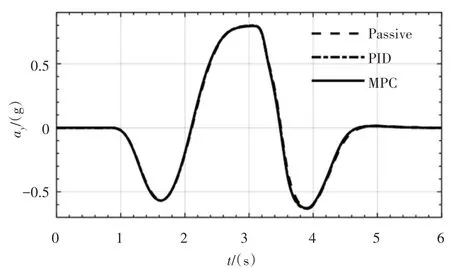
图8 侧向加速度Fig.8 Lateral Acceleration

预测时域Np对MPC 主动防侧倾控制的影响，如图9 所示。从图中可以看到，相比被动横向稳定，MPC主动控制可以显著降低车身侧倾角，而预测时域Np是影响MPC控制器性能的敏感参数。由于Np是对系统未来状态的预测长度，Np越大，预测长度越长，响应速度越快，而仿真结果正好验证了这一结论。但当Np过大时，对计算资源要求较高，虽然控制器响应速度很快，但稳定性降低，图中显示在4s之后侧倾角出现了较大幅度的反弹。因此，通过综合评价，选取Np=45，保证了响应速度和稳定性的权衡。

在确定了Np之后，调整控制时域Nc，研究Nc对MPC 主动防侧倾控制的影响。随着Nc的变化，MPC控制器的性能没有明显的改善，如图10所示。当Nc取15、25、35时，响应速度都有小幅提升，但在4s之后出现小幅度的反弹，稳定性下降。故综合考虑计算量和控制性能，选取Nc=20。MPC控制综合考虑了系统性能和控制输入的最优化，故性能和输入的加权系数也是影响控制器效果的关键参数。根据侧倾角和侧倾辅助力矩的量级，确定了前、后悬架的性能加权系数为1，输入加权系数10-5。为了平衡前、后悬架的防侧倾性能，同时有效利用前、后悬架电机的最大输出扭矩，改变前、后悬架的性能加权系数进行仿真。前悬架侧倾角加权系数对侧倾角的影响，如图11所示。

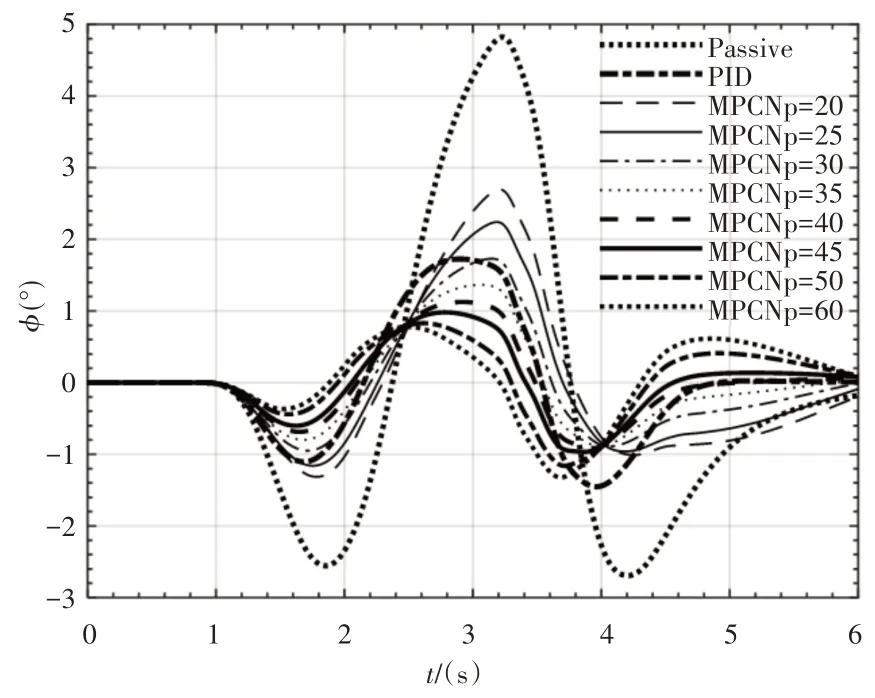
图9 预测时域Np对侧倾角的影响Fig.9 Influence of Predictive Horizon Np on Roll Angle

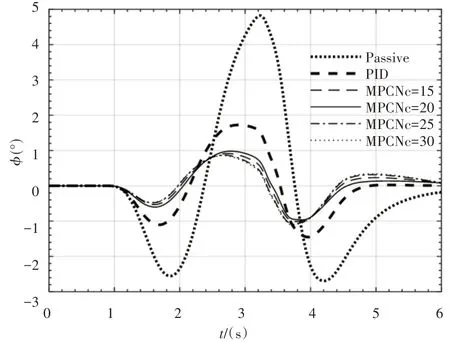
图10 控制时域Nc对侧倾角的影响Fig.10 Influence of Control Horizon Nc on Roll Angle

由于前悬架的防侧倾力矩系数和前稳定杆纵横比均大于后悬架，故前悬架横向稳定杆的侧倾辅助力矩需求较大，如果前悬架侧倾角加权系数设置偏大，侧倾辅助力矩会发生饱和。选取前悬架侧倾角加权系数qf∈[1，5]，图11 的仿真结果显示，当qf增大时，系统响应加快，但最大侧倾角增大，4s之后的侧倾角趋稳速度减小，同时，当qf>2时电机输出力矩会发生饱和。因此，确定qf=1。后悬架侧倾角加权系数qr对侧倾角的影响，如图12所示。qr对侧倾角的影响不大，但影响趋势与前悬架类似，故选取qr=1。

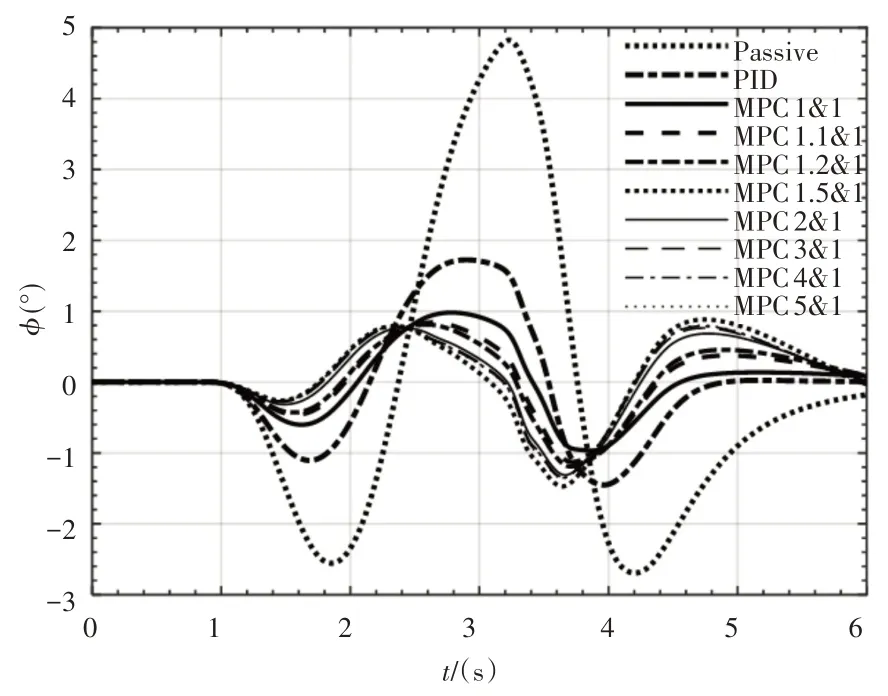
图11 前悬架侧倾角加权系数qf对侧倾角的影响Fig.11 Influence of Front-Suspension Roll Angle Weight qf on Roll Angle

根据图9～图12的仿真试验，确定了相对最优的MPC控制器的参数，其仿真结果，如图13所示。由图可知，MPC控制器的侧倾角被控制在-0.966°到0.980°范围内，相比被动悬架和PID 控制，最大值分别降低了80%和44%，MPC控制的响应速度比PID控制更快，响应快0.2s左右。因此，MPC控制器拥有更好的防侧倾性能，转向时的车身姿态最平稳。

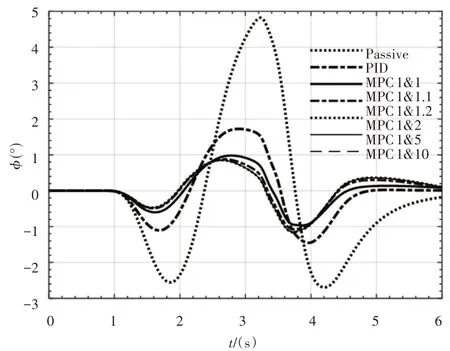
图12 后悬架侧倾角加权系数qr对侧倾角的影响Fig.12 Influence of Rear-Suspension Roll Angle Weight qr on Roll Angle

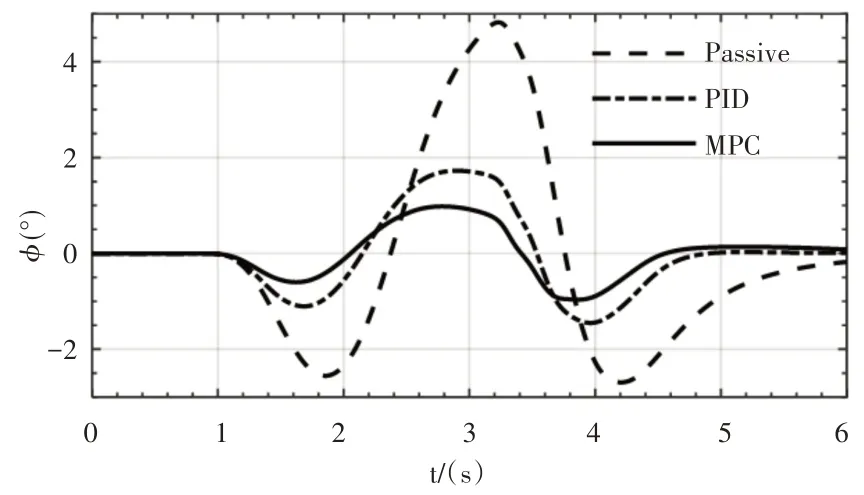
图13 侧倾角Fig.13 Roll Angle

前、后悬架的防侧倾辅助力矩比较，如图14所示。从力矩曲线可知，电机输出力矩的整体趋势和防侧倾力矩一致，在相同的工况下，PID 控制和MPC 控制的最大防侧倾力矩分别达到2817N·m和3035N·m，MPC控制利用比PID控制多输出8%左右的力矩，提供了44%的性能提升，获得了系统性能和控制输入的最佳平衡。前、后悬架电机输出力矩比较，如图15所示。

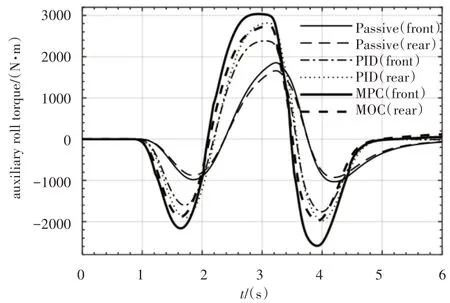
图14 防侧倾辅助力矩Fig.14 Anti-Roll Auxiliary Roll Torque

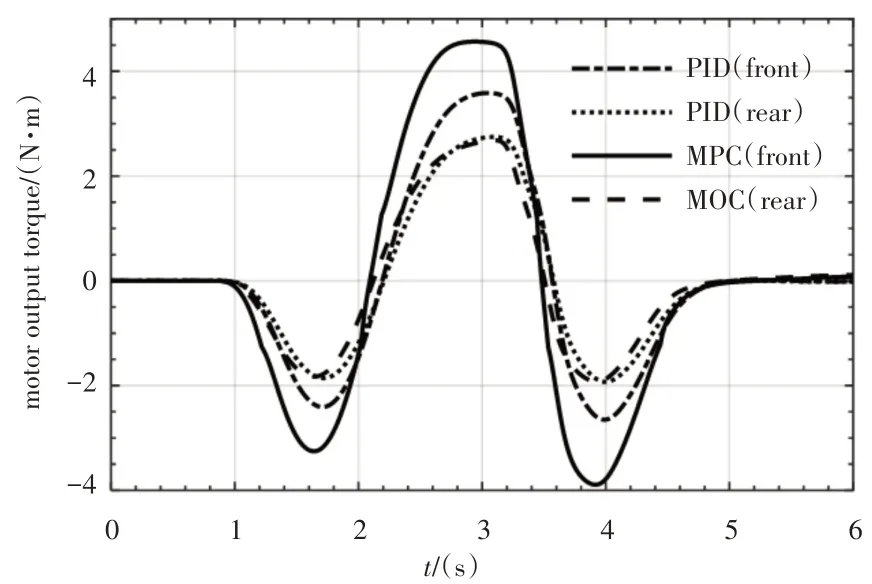
图15 电机输出力矩Fig.15 Motor Output Torque

仿真试验设定前、后稳定杆电机的最大输出力矩为5N·m，试验中要避免发生力矩饱和。图中显示PID控制和MPC控制的最大力矩需求分别是3.6N·m 和4.5N·m，都未发生力矩饱和，符合试验要求。主动稳定控制的电机功率需求，如图16所示。从图中可知，整个双移线工况（0～6）s试验过程中，MPC控制的前、后悬架电机最大瞬时功率和平均功率都比PID控制要小，具体功率值，如表2所示。因此，MPC控制较小的能量消耗实现了更优的防侧倾控制，防侧倾性能令人满意，理想的防侧倾力矩在SRM上是可实现的，响应速度快，能耗在可接受的范围内。

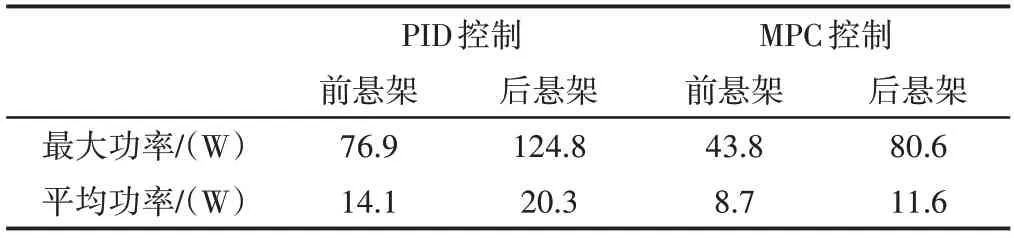
表2 电机功率Tab.2 Motor Power

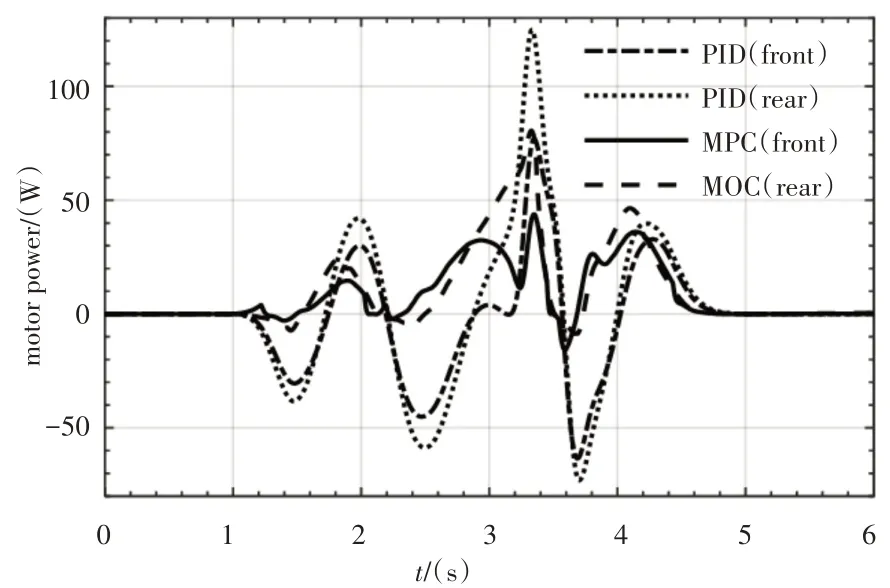
图16 电机功率Fig.16 Motor Power

7 结论

本研究针对电机式主动横向稳定杆完成了电机和整车系统的数学建模，设计了模型预测控制器来实现防侧倾控制，并利用Matlab/Simulink和Carsim的联合仿真验证了模型预测控制器的有效性。研究结果表明：

（1）相比于被动悬架和PID控制，模型预测控制可以有效地抑制由侧向加速度引起的车身侧倾运动，降低车身侧倾角，并使车身快速稳定；（2）预测时域和输出性能加权系数是影响模型预测控制器性能的敏感参数，在设计控制器时应合理选取；（3）相比PID控制，模型预测控制的能耗更小，这是性能和控制输入权衡考虑的结果；（4）理论上防侧倾力矩可以通过电机作动器来实现，为下一阶段的试验提供了理论基础。