组合梁预应力混凝土桥面板承载力试验研究

曾明辉张协力

（1.江西省交通投资集团有限有限公司，南昌 330025；2.同济大学土木工程学院，上海 200092）

0 引言

钢-混凝土组合结构桥梁可充分发挥钢材和混凝土材料的性能，具有良好的经济性和适用性，其中钢板组合梁桥因其结构简单，制造、施工便利而在中小跨径的公路桥中得到广泛应用。根据钢主梁的数目把组合梁截面形式分为双主梁和多主梁断面。在欧美及日本等地，钢板组合梁桥的发展趋势均为少主梁桥逐渐代替多主梁桥［1］。法国在1982年前后集中力量对组合结构桥梁进行了研究，对传统的钢板组合梁体系进行了大幅度的简化，双主梁钢板组合梁成为了中小跨径桥梁建设的主梁方案，并于1985年制定了双主梁钢板组合梁桥设计指南［2-4］；日本桥梁建设协会在《新型钢桥的诞生II（改订版）》中建议，当桥宽超过12 m时，可采用3～4片主梁，小于12 m时建议采用双主梁形式［5］。刘永健等［6］针对双主梁钢板组合梁在我国中小跨径桥梁中的应用进行了分析，总结了其在适用桥宽、桥面板、钢主梁及横梁设计、施工难度和经济性等的特点。我国的学者对钢板组合梁的设计参数进行了一些研究，但双主梁钢板组合梁的应用在我国还处于起步阶段［7-10］。

组合梁桥比混凝土梁桥自重轻、刚度小，活载占总设计荷载的比例大，桥面直接承受车轮荷载及其冲击作用，钢筋混凝土桥面板的强度及抗裂性能在结构设计中起控制作用［11］。Ockleston［12］测试了三层钢筋混凝土结构的极限承载力，发现其极限承载能力比塑性铰线理论值高3～4倍，常用的极限方法从理论上很难得到满意的结果，往往需要根据试验来加以修正，Girolami［13］对水平方向可自由移动的混凝土面板进行了试验研究，结果也表明混凝土面板的抗弯承载力较塑性铰线理论计算值偏大。加拿大安大略省交通运输部组织对钢筋混凝土桥面板的静力及疲劳受力性能进行了系统的研究，其中包括一系列实桥试验，得出结论：板平面内约束的存在将提高板的极限承载能力，研究成果被编入了高速公路桥梁设计规范［14］；纽约公路局的试验研究表明在设计荷载作用下，桥面板钢筋的应力较小，最终破坏形态为钢-混凝土连接位置的剪切破坏［15］。Fang［16］与Cao［17］通过试验研究了活载作用下主梁挠曲对钢筋混凝土桥面板受力性能的影响，并与有限元计算结果进行对比分析，提出了钢筋混凝土桥面板的配筋优化方法。

现有的钢筋混凝土桥面板的研究多针对混凝土桥梁，研究成果多基于缩尺试验得出。与混凝土桥梁相比，组合梁腹板的面外刚度小，腹板对混凝土桥面板的约束作用弱，对于大跨径预应力混凝土桥面板，其极限承载力与破坏形态也有所区别。为探究双主梁钢板组合梁桥预应力混凝土桥面板的受力性能，本文开展了足尺的预应力混凝土桥面板模型试验，研究了其极限承载力及破坏形态，得到了桥面板的安全储备情况。

1 试验概况

1.1 背景工程

针对我国高速公路实际情况，单幅桥梁宽度多在11.5～12.75 m，本文结合一实际工程开展研究。其预应力混凝土桥面板宽度为12.65 m，支承在间距为7.05 m两片钢主梁上；混凝土桥面板采用预制桥面板，采用C50混凝土，按A类预应力构件设计，桥面板在横向跨中位置及钢梁支承位置的厚度分别为30 cm和40 cm。混凝土板横向每隔500 mm设置一道横向预应力束，预应力钢束采用4-φS15.2钢绞线，张拉应力为1 395 MPa。桥面板横向采用全宽预制，纵桥向预制节段长度为3 m，预制桥面板吊装就位后通过浇筑横向宽度0.5 m湿接缝形成整体，混凝土桥面板与钢主梁通过成束的群钉连接。实际工程的标准断面如图1所示。

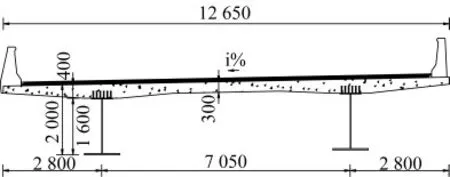
图1 结构断面图（单位：mm）Fig.1 Cross section of prototype bridge structure（Unit：mm）

1.2 试件设计与加工

设计制作了1个预应力混凝土桥面板试件PCTS，试件混凝土板部分在厚度及长度方向尺寸与背景工程节段预制板相同，宽度方向考虑实际加载条件，取1.5 m。试件的钢梁梁高均为0.9 m，顶板宽度为750 mm，底板宽度为400 mm，顶板、底板和腹板板厚均为16 mm。试件整体尺寸如图2所示。

图2 试件PCTS整体布置图（单位：mm）Fig.2 Plan and elevation of specimen（Unit：mm）

混凝土板横向每隔500 mm设置一道横向预应力束，预应力束采用4-Φs15.2钢绞线，张拉应力为1 339 MPa，预应力筋布置如图3所示。板内纵桥向钢筋直径22 mm，间距100 mm；横桥向钢筋直径16 mm，间距125 mm；箍筋直径12 mm，间距400 mm，采用HRB400带肋钢筋。纵、横筋均采用双层配筋，试件普通钢筋布置如图4所示。

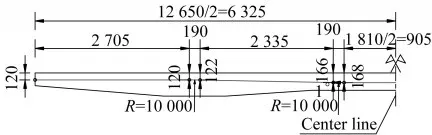
图3 混凝土桥面板预应力筋布置图（单位：mm）Fig.3 Elevation of prestressd tendon of deck slab（Unit：mm）

图4 试件钢筋布置图（单位：mm）Fig.4 Reinforcement arrangement of concrete deck slab（Unit：mm）

混凝土桥面板预制后整体吊装至钢主梁上，再浇筑群钉孔形成组合结构，混凝土养护28 d后张拉预应力。

1.3 加载及测试

试件PCTS水平安置于地面，钢梁与地面间通过高强砂浆填充空隙。采用跨中单点加载，模型加载示意图如图5所示。在正式加载开始前进行预加载，预载荷载为开裂荷载的30%，分三级施加，持荷15 min，最后分两级卸载；根据预加载数据，判断加载设备及测试仪器是否正常工作，调整故障设备后正式加载。正式加载第一阶段荷载值从0 kN至开裂荷载，分四级加载到开裂荷载的80%，之后以千斤顶最小的加载增量加载至混凝土板开裂；第二阶段加载至屈服荷载，每级20 kN，持荷15 min后采集数据，每加载100 kN，观测一次裂缝；第三阶段连续加载至试件破坏，控制在5 min内缓慢加载，加载过程中连续采集试验数据。试验加载现场如图6所示。

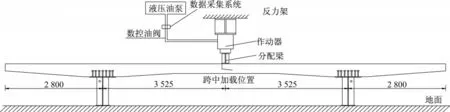
图5 模型加载示意图（单位：mm）Fig.5 Load introduction（Unit：mm）

图6 试验加载现场Fig.6 Loading instrumentation

1.4 测点布置

在试件的钢梁支承截面及跨中加载点截面布置位移计以监测试验过程中试件的变形；在跨中截面的底层横向钢筋与混凝土板下表面、支承截面的顶层钢筋与混凝土板上表面布置应变计以测量试件的应变，试件测点布置如图7所示。

图7 试件测点布置（单位：mm）Fig.7 Arrangement of measuring points of specimen（Unit：mm）

2 试验结果

2.1 材料性能

测试了与试件相关主要受力材料的力学性能。其中直径为16 mm和22 mm钢筋的屈服强度分别为441.0 MPa和429.0 MPa，抗拉强度分别为632.1 MPa和623.2 MPa。边长150 mm标准立方体混凝土试块28 d抗压强度为61.6 MPa。

2.2 荷载-位移曲线及破坏形态

正式加载过程中实时监测试件的位移、应变响应，并阶段性观测试件表面裂缝发展。

试件PCTS在加载初期表现出良好的弹性性能，跨中变形随荷载增加而增大，当荷载达到240 kN时，混凝土板跨中位置下表面出现裂缝。随着荷载等级的提高，混凝土板下表面裂缝数量逐渐增多，裂缝宽度不断增大，侧面裂缝不断向上发展。在荷载达到600 kN时桥面板跨中位置下层横桥向钢筋先出现屈服，随后加载位置截面的上表面混凝土被压溃，跨中位置混凝土板下表面形成贯通裂缝，试件的极限荷载为640 kN，试件的破坏形态为典型的抗弯破坏。试件的破坏形态如图8所示。

图8 试件破坏形态Fig.8 Failure modes of specimen

试件PCTS的荷载-位移曲线如图9所示，试件经历了开裂前的线弹性受力阶段和开裂后的非线性受力阶段。当荷载达到240 kN时荷载-位移曲线发生转折，是由于跨中处底面混凝土开裂，随着荷载的增加，曲线斜率逐渐减小。试件的荷载-曲率曲线如图10所示，由图10可知，当荷载达到约600 kN时，试件已几乎丧失抗弯承载力；当荷载达到640 kN时，试件达到抗弯承载力而破坏，破坏时混凝土板跨中截面最大挠度为90 mm。

图9 跨中荷载-位移曲线Fig.9 Load-deflection curves at mid-span

图10 跨中荷载-曲率曲线Fig.10 Load-curvature curve at mid-span

2.3 钢筋应变

试件跨中截面底层钢筋荷载-应变曲线如图11所示。在混凝土板开裂前，各测点钢筋应变随着荷载的增加而线性的增大。当荷载达到240 kN时，混凝土板下表面产生裂缝，荷载-应变曲线产生明显的转折；随着荷载的持续增大，曲线的斜率随着荷载的增加而减小，钢筋表现出非线性受力特性。当荷载接近600 kN时，部分底层钢筋开始屈服，钢筋应变迅速增大，随着加载的继续，底层钢筋相继进入屈服，直至荷载达到640 kN试件破坏，钢筋荷载-应变曲线均已趋向水平。

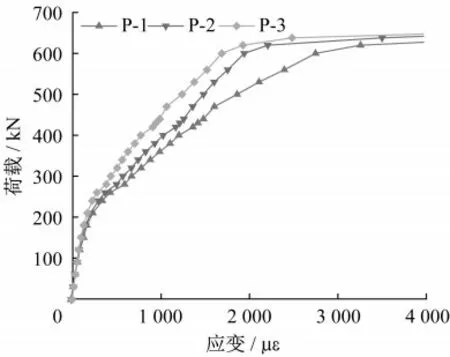
图11 试件PCTS跨中处底层钢筋应变Fig.11 Load-strain curves of reinforcements embedded in bottom concrete slab at mid-span

2.4 混凝土应变

试件跨中截面混凝土荷载-应变曲线如图12所示。在加载初期顶层混凝土表现出良好的弹性受力性能，混凝土压应变值随着荷载的增加而线性的增加，当荷载达到约500 kN时曲线的斜率减小，此时混凝土压应变达到约1 200 με，随着荷载达到极限荷载640 kN，混凝土最大压应变达到3 600 με，并发生压溃破坏。由底层混凝土荷载-应变曲线可知，在混凝土板开裂前，各测点混凝土应变随着荷载的增加而线性增大，当荷载达到150 kN时，曲线发生明显转折，反映出混凝土内部的初始缺陷不断发展，使得混凝土发生应力重分布，并导致混凝土应变随着荷载的增加而减小。随着荷载持续增加，试件下表面混凝土板裂缝充分发展，当裂缝直接穿过应变测点位置后，混凝土应变急剧增大，随后试件即发生破坏。

图12 试件PCTS跨中处混凝土应变Fig.12 Load-strain curves of concrete at mid-span

2.5 混凝土裂缝

当荷载达到240 kN时，混凝土板下表面出现初始裂缝，宽度为0.03 mm；随着荷载的增加，裂缝对称的出现在跨中截面左右两侧。当荷载增大到300 kN时，已有裂缝贯通板宽，最大裂缝宽度为0.10 mm。当荷载增大到360 kN时，裂缝宽度达到0.12 mm。在360 kN后，基本无新的裂缝出现，最大裂缝宽度不断变大，当荷载增大到440 kN时，裂缝宽度达到0.2 mm。混凝土裂缝分布随荷载的变化如图13所示，长裂缝的间距为80～120 mm，与纵向分布钢筋的间距相近。

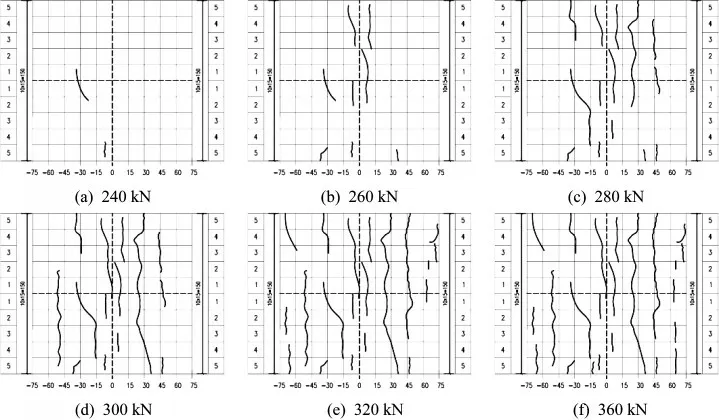
图13 裂缝分布图（单位：cm）Fig.13 Crack distribution（Unit：cm）

最大裂缝宽度随荷载等级的变化如图14所示，试件开裂荷载为240 kN，当荷载达到440 kN时，最大裂缝宽度为0.2 mm，达到混凝土桥涵规范中的正常使用极限状态下裂缝宽度的限值。

图14 最大裂缝宽度测量图Fig.14 Maximum crack width

3 桥面板的极限承载力及安全富余度

3.1 极限承载力计算

对于采用纵向体内钢筋的矩形截面受弯构件，其正截面抗弯承载力Mud按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）［18］（以下简称《桥涵设计规范》）的规定进行计算，其计算公式如式（1）所示：

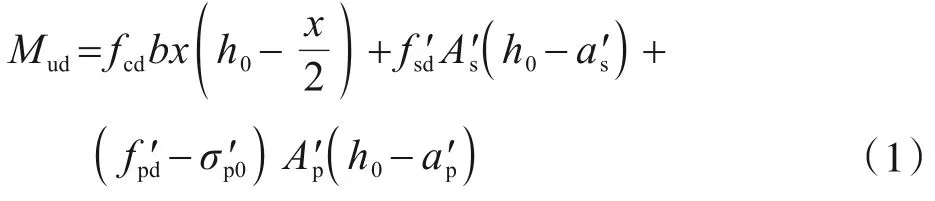
式中：fcd是混凝土轴心抗压强度设计值；fs′d是纵向普通钢筋抗压强度设计值；fp′d是纵向预应力筋抗压强度设计值；A′s为受压区纵向普通钢筋的截面积；A′p是纵向预应力筋截面积；a′s与a′p分别为普通钢筋与预应力合力点至受压区边缘的距离；b为矩形截面宽度；h0是截面有效高度；x为混凝土受压区高度，应按式（2）计算：

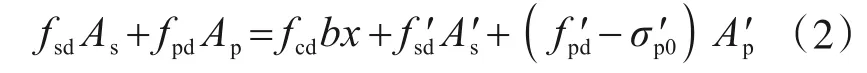
且应符合式（3）要求，ξb为相对界限受压区高度。

使用材料强度的设计值进行正截面抗弯承载力的计算，取C50混凝土的轴心抗压强度为22.4 MPa，HRB400钢筋的设计强度为330 MPa，预应力筋的抗压强度设计值为390 MPa，计算所得Mud为624.3 kN·m；采用材性试验所得的强度实测值计算所得Mur为987.1kN·m；桥面板加载试验得到的截面抗弯承载力Mut=1 128.0 kN·m，试验值Mut与Mur较为相近。结构抗弯承载力试验值与计算值的比值Mut/Mud=1.8。

结构除按承载能力极限状态的要求进行承载力计算外，还应满足正常使用极限状态下的使用要求，《桥涵设计规范》中最大裂缝宽度Wcr的计算公式为

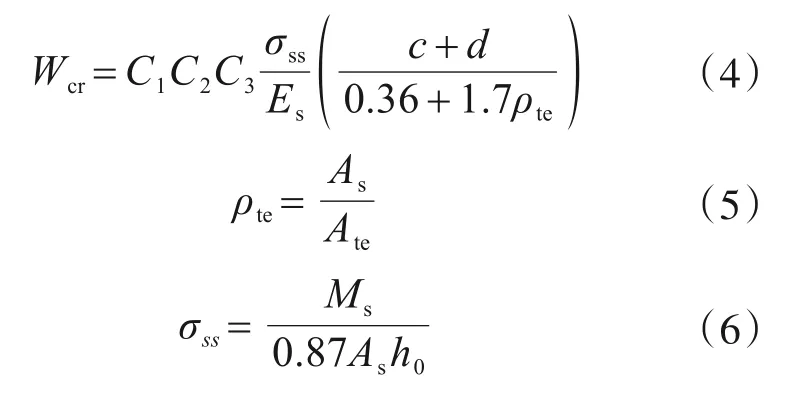
式中：C1，C2，C3是与材料及构件受力性质有关的系数；σss是钢筋应力；c是混凝土保护层厚度；d是受拉钢筋的直径；ρte是受拉钢筋的有效配筋率；Ms是按频遇组合作用下计算的弯矩值；As是全部受拉钢筋的面积；h0是截面有效高度。

计算可得当最大裂缝宽度达到0.2 mm时的弯矩值Msd=405.0 kN·m，桥面板试验中裂缝宽度达到0.2 mm时的截面弯矩值Mst=775.5 kN·m，相同裂缝宽度对应的极限弯矩试验值与计算值的比值Mst/Msd为1.9。

3.2 荷载作用效应计算

作用在桥面上的车轮压力通过铺装层扩散在混凝土桥面板上，按《公路桥涵设计通用规范》（JTG D60—2015）［19］（以下简称《通用规范》）规定，取车轮与桥面的接触面为200 mm×600 mm的矩形，荷载在铺装及找平层内偏安全地假定呈45°角扩散，最后作用于钢筋混凝土桥面板的矩形压力面沿纵向长度a1=400 mm，沿横向宽度b1=800 mm。按单向板计算桥面板的有效工作宽度，在板的中央地带，对于单独一个车轮荷载作用，有效工作宽度a=a1+l/3且a≮2l/3，故a=4 700 mm，其中l为板的跨径。取单宽半条计算车辆荷载效应，考虑车轮的最不利布置与冲击效应，汽车荷载在1 m宽简支板条中产生的跨中弯矩M0p=76.50 kN·m，考虑主梁的不均匀下沉和扭转刚度的影响，活载产生在桥面板跨中弯矩Msp=0.7M0p=53.55 kN·m。单位板宽的跨中恒载弯矩Msg=0.7M0g=18.3 kN·m，M0g为相同跨径简支板跨中恒载弯矩。

3.3 设计安全系数分析

根据JTG D60—2015的规定对桥面板进行承载能力极限状态设计，计算作用效应的基本组合：

式（7）中结构重要度系数γ0取1.0，永久作用效应分项系数γG1取1.2，车辆荷载效应分项系数γQ1取1.8，计算得到单位宽度桥面板基本组合作用的效应值为118.32 kN·m，单位宽度桥面板的正截面抗弯承载力Mud，r按《桥涵设计规范》计算为416.2 kN·m，则预应力混凝土桥面板按承载能力极限状态设计的安全系数为Mud，r/γ0Mud，l=3.5，结构设计的安全富余度较大。

根据《桥涵设计规范》的要求，正常使用极限状态下A类预应力混凝土构件，应满足：

B类预应力混凝土受弯构件在结构自重作用下控制截面受拉边缘不得消压，同时应按频遇组合作用并考虑长期效应的影响验算最大裂缝宽度。其中σst、σlt分别为作用频遇组合、准永久组合下截面边缘混凝土的法向拉应力，σpc为预加力在截面边缘产生的混凝土预压应力，按式（10）计算：

式中：Np为预加力合力；An为净截面面积；In为净截面惯矩；epn为截面偏心距；yn为截面重心至计算纤维处距离。

按上述两类设计原则计算正常使用极限状态下的桥面板试件的极限弯矩，并与试验值进行比较得按正常使用极限状态设计的安全系数，计算结果如表1所示。

表1 按正常使用极限状态下设计的安全系数Table 1 Design safety factor under serviceability limit state

4 结论

本文通过开展足尺模型试验，从挠度、钢筋应变、混凝土裂缝等方面研究了双主梁钢板组合梁预应力混凝土桥面板受力性能，得到了极限承载能力和破坏形态；根据《桥涵设计规范》与《通用规范》计算得到了实际桥面板结构在两个极限状态下的荷载效应及抗力，对比试验值与计算的结果，得到了双主梁钢板组合梁桥预应力混凝土桥面板的安全储备情况，具体结论如下：

（1）开展了足尺双主梁钢板组合梁钢筋混凝土桥面板模型的单点跨中加载试验，得到结构的破坏形态为抗弯延性破坏，桥面板跨中截面的抗弯极限承载力为1 128.0 kN·m，当达到极限承载力时，桥面板下层钢筋屈服，上表面混凝土压溃，结构产生明显的塑性变形。

（2）预应力混凝土桥面板的开裂弯矩为423.0 kN·m，最大裂缝宽度为0.03 mm；当荷载达到440 kN时，跨中截面弯矩为775.5 kN·m，最大裂缝宽度为0.20 mm，达到《桥涵设计规范》规定正常使用极限状态下裂缝宽度限值。

（3）根据《桥涵设计规范》计算得到预应力混凝土桥面板的抗弯承载力并与试验结果进行对比；桥面板发生弯曲破坏时的极限弯矩试验值与计算值的比值Mut/Mud为1.8；当裂缝宽度都达到0.2 mm时极限弯矩试验值与计算值的比值Mst/Msd为1.9。

（4）根据《通用规范》与《桥涵设计规范》计算得到不同作用组合下的荷载效应，与抗弯承载力设计值对比得到承载能力极限状态下的设计安全系数为3.5，在正常使用极限状态下，按A类预应力构件进行设计的安全系数为2.5，按B类预应力构件进行设计的安全系数为3.8。