中等跨度轨道交通桥梁有载频率研究

向桂林吴定俊周建民

（1.同济大学建筑工程系，上海 200092；2.同济大学桥梁工程系，上海 200092）

0 引言

随着社会经济、人口的不断发展，城市的交通运输面临着严峻的考验，传统的出行方式无法解决当前复杂的交通状况。目前地铁在大中城市的广泛引入开拓了城市可利用空间，其具有运量大、安全、快速、无尾气、自动化程度高、无污染的优点，经过百年发展已经技术成熟，成为城市交通的主动脉。但因开发地下空间造价较高，易受到当地经济条件限制，钢轮-钢轨走行系统使地铁仍存在噪声污染、线路设计具有局限性等无法克服的缺陷。因此，跨座式轨道交通应运而生。

如图1所示的跨座式轨道交通是我国引进的一种新式轨道交通，最高速度和平均速度分别为80 km/h，40 km/h。其转弯半径小、占地少、费用低、经济实惠等优势在世界各国获得了青睐和发展。纵观国内外一些轨道交通发展成熟的城市，公共交通系统的多元化是其主要特色，其中地铁一般占到三分之一左右。因此，我国的单轨、轻轨和有轨电车等城市轨道交通形式还有很大的发展空间。

图1 重庆市二号线轨道交通Fig.1 Chongqing city line 2 rail transit

跨座式单轨交通桥梁横向尺寸往往较小，重庆跨座式单轨单线式标准简支轨道梁［1］的梁宽仅0.85 m，如图2所示，深圳的比亚迪云轨更是达到了0.7 m。另外，由于跨座式单轨交通桥梁上部结构仅为单薄的轨道梁，其自重会显著小于同等跨度的公路、铁路以及普通地铁桥梁。因此，本文从研究跨座式桥梁与普通公路、铁路等桥梁的车桥质量比差异，计算分析它们对桥梁有载频率的影响。

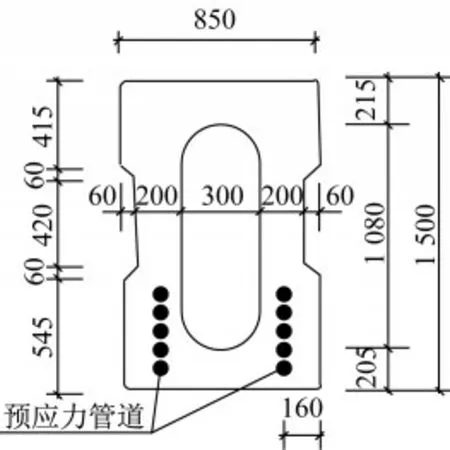
图2 跨座式单线轨道梁标准截面图（单位：mm）Fig.2 Standard section view of straddle single track beam（Unit：mm）

1 不同交通类型桥梁车桥设计参数分析对比

1.1 不同类型交通桥梁梁跨质量比

根据重庆市二号线轻轨交通工程，单线跨座式标准轨道梁跨中截面面积约为0.92 m2，32 m跨度的轻轨梁重量不足100 t；而公路、高铁单线式桥梁在32 m的跨度，重量均达到400 t以上［2］，大部分集中在500～600 t范围；客货共线铁路重量同高速铁路桥梁相当，32m跨度桥梁重量达到367 t［3］；广州地铁4号线30 m跨度的整孔箱梁起吊重量可达到4 100 kN［4］。其余参数如表1所示。

表1 32 m跨度的各类桥梁重量对比表Table 1 Comparison table of various bridge weights with 32 m span

在跨座式单轨梁中，截面很小，桥梁整体重量远小于同等跨度的其他桥梁，对于公路、铁路两类单线式桥梁，重量都达到了跨座式单轨的5倍以上。值得指出的是，对于部分32 m跨度的双线箱形桥梁主梁重量可达到927 t［5］，其质量更是远远超过跨座式单轨。因此，对于跨座式单轨梁，梁体质量相对很小，在考虑列车荷载后，可能会对梁体有载频率的变化产生较大影响。在跨座式单轨计算中，不同于普通公路、铁路桥梁，应当关心其桥梁质量较小，导致车桥质量比较大所带来的对桥梁结构动力性能的影响。

1.2 不同类型交通车辆荷载比

《跨座式单轨交通设计规范》规定，在进行轨道梁设计时应当按照远期规划车型及车辆编组施加列车活载，跨座式单轨列车主要采用4轴车辆模型，轴重满载时宜取为110 kN，如图3所示。

图3 跨座式单轨列车荷载图示Fig.3 Straddle monorail train load diagram

对于铁路荷载，规范中主要由集中力和分布力表示，对于不同铁路类型，荷载图示也不一样，本文以高速铁路荷载为例，集中力部分为200 kN，分布力为64 kN/m，如图4所示。

图4 高速铁路列车荷载图示Fig.4 High-speed railway train load diagram

公路汽车荷载分为Ⅰ级汽车荷载和Ⅱ级汽车荷载，均采用相同的车辆荷载标准值，车辆重力标准值取550 kN，轮距为1.8 m，车辆外形尺寸为15 m×2.5 m，本次研究高速公路荷载取为汽车荷载，不考虑车道荷载，图5为汽车荷载图示。

图5 公路汽车荷载图示Fig.5 Highway car load diagram

客货共线铁路列车荷载统一采用我国客货共线（ZKH）和货运专线（ZH）铁路设计的中-活载图示中的4个250 kN的集中荷载代表机车车辆邻重和邻轴效应，85 kN/m的均布荷载代表货车车辆每延米重效应，z为活载等级系数，其中客货共线铁路按1.0取用，如图6所示。

图6 客货共线铁路列车荷载图示Fig.6 Train load diagram for passenger and freight trains

根据《地铁设计规范》（GB 50157—2013），采用地铁列车活载如图7所示，轴重取为130 kN。同跨座式轨道交通荷载类似，采用4轴车辆模型。对于双线地铁，对两条线路同时进行列车加载，考虑双线地铁同时达到效应最大值的可能性较低，取0.9的降低系数。

图7 双线地铁列车荷载图示Fig.7 Two-line subway train load diagram

最后均以32 m中等跨度桥梁的最大可能加载，比较跨座式轨道梁与高速公路、高速铁路、地铁等桥梁荷载单位长度（m）的大小，结果见表2。高速铁路列车荷载单位长度达到76.2 kN，是跨座式列车荷载34.38 N的2.22倍；而对于公路荷载，两者较为接近，达到35 kN；地铁荷载是跨座式列车的1.91倍，达到65.81 kN；其中客货共线铁路荷载最大，单位长度荷载为跨座式的2.89倍，达到99.25 kN。

表2 单位长度（m）的列车荷载Table 2 Train load per unit length（m）

1.3 各式类型桥梁车桥质量比

桥梁有载频率的计算主要由车桥质量比控制。因此，本文在已总结归纳的基础上，进一步研究跨座式单轨桥梁车桥质量比与公，铁等桥梁的差距。

Nutrien是全球最大的作物投入和服务提供商，在帮助种植者以可持续方式增加粮食产量方面发挥着关键作用。它在世界范围内生产和分销超过2500万吨的钾肥、氮肥和磷肥产品。凭借这一能力及其领先的农业零售网络，能够满足客户需求。它以长远眼光经营，并致力于与其利益相关方合作，解决其经济、环境和社会优先事项。其综合投资组合的规模和多样性提供了稳定的收益基础，多重增长途径和向股东返还资本的机会。

列车荷载大小，桥梁自重及其车桥质量比的数值如表3所示。（其中重力系数g取9.8 N/kg）跨座式单轨梁的车桥质量比为1.59，列车质量显著大于桥梁质量，而其他4类桥梁比值均在1以下。客货共线铁路列车质量略小于桥梁质量，车桥质量比为0.88。其中，单向双车道公路桥梁的车桥质量比最小，仅为0.33。

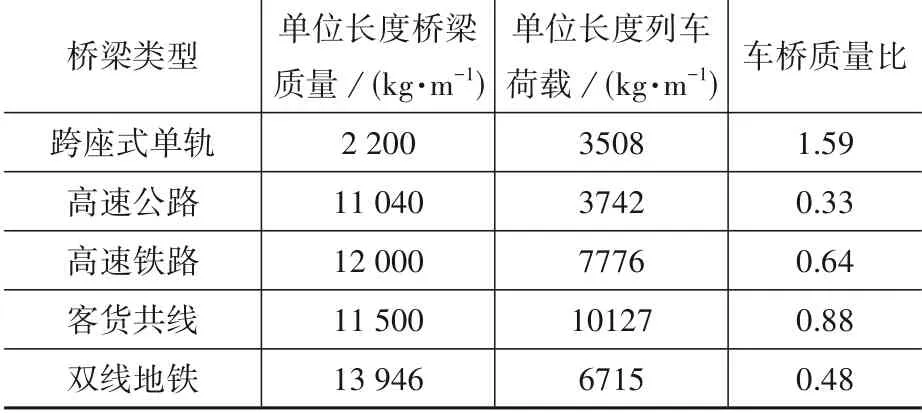
表3 32 m跨度各式桥梁车桥质量比Table 3 The vehicle-bridge mass ratio of various bridges with 32 m span

2 简支梁有载频率计算方法

本文从考虑列车匀速移动的状态下，计算桥梁在列车荷载下的频率变化。假设简支梁为Euler-Bernouli梁，忽略剪切变形和转动惯量的影响［6］，并假设桥梁为均质等截面梁，不考虑阻尼影响，本文考虑车辆过桥时车桥系统的质量变化对桥梁有载频率的影响，不考虑桥梁刚度变化的影响作用。

计算简图如图8所示。

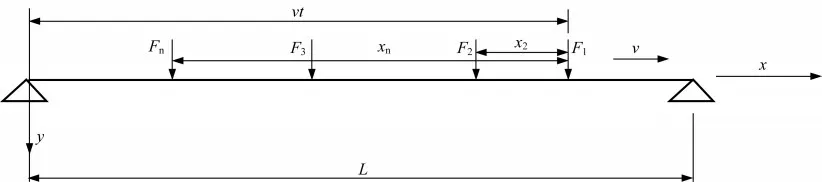
图8 有载频率计算简图Fig.8 Load frequency calculation diagram

简支梁在多个外荷载作用下的振动微分方程为

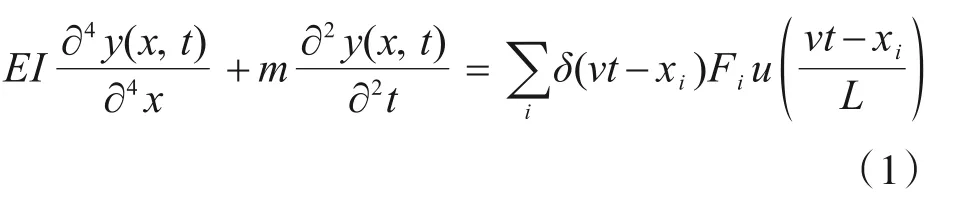
式中：m为梁单位长度的质量；EI为梁的抗弯刚度；y(x，t)为x处时刻t的位移；δ为Dirac函数；u为分段函数。

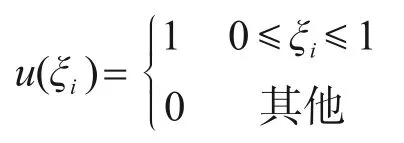
在该简支梁中，由振型叠加原理，假设梁的振动为

式中：φn(x)为振型，与时间t无关；An(t)为模态坐标，是时间t的函数；N为所取模态数。

对于简支梁振型函数如式（3）所示。

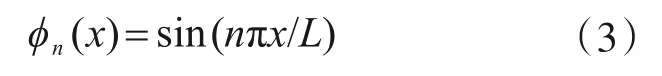
将式（2）代入式（1）并利用阵型正交性，等式两边乘以φn(x)=sin(nπx/L)，并对x从0到L积分，得到解耦的强迫振动方程如下：

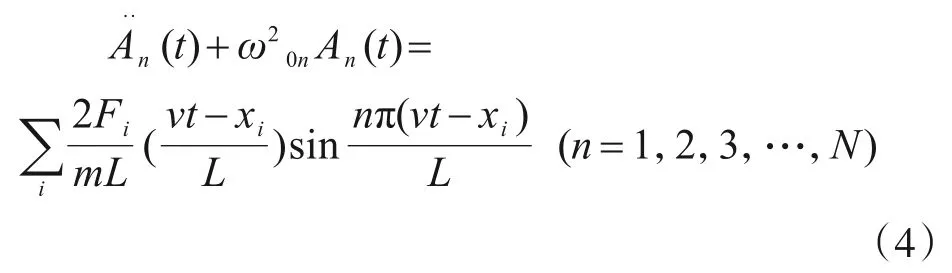
式中，ω0n为等截面简支梁的各阶无载固有圆频率。

通过牛顿第二定律，将车对桥的作用力作用于相应桥面位置处，该作用力由移动质量产生，则在任一时刻t，荷载对桥梁的作用力等于重力与其惯性力的合力，即

式中：mi为各个移动质量；g为重力加速度为个移动质量加速度。

假定移动质量在移动过程中始终与梁保持接触，则也是各质量作用点处梁的加速度。将式（5）代入式（4），各阶振型的强迫振动微分方程为

由式（2）可得：

把式（7）代入式（6）可得：

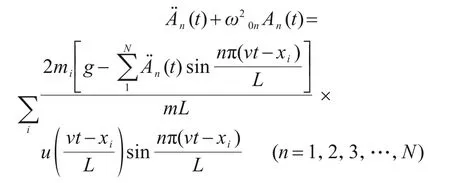
当取n=1时，可得第一阶有载频率，表达式见式（8）。

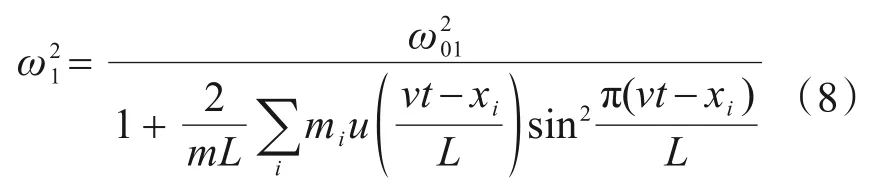
式中，ω1为等截面简支梁一阶有载圆频率，一阶工程频率f1=ω1/2π。

3 不同类型交通形式桥梁有载频率计算分析

3.1 不同类型交通形式桥梁有载频率基频分析

根据有载频率推导，采用Matlab语言编写了计算程序，分析不同形式桥梁在32 m跨度下有载频率的变化。由于公路、铁路荷载图示与跨座式单轨荷载有较大区别，而在桥梁实际计算中，跨中弯矩为桥梁的主要控制因素，最不利情况也最容易发生在跨中截面，且为了便于计算分析比较最终结果，现将各类桥梁的荷载通过跨中弯矩等效方法，将其转换为跨座式列车荷载的形式，得到各类型列车荷载的轴重。

由于弹性模量在各式桥梁中总体差距较小，且列车运行速度主要影响桥梁有载频率的变化速度［6］，而对有载频率的变化幅值影响很小，故本例选取跨座式单轨桥梁中的列车运营速度v=30 km/h，弹性模量E=3.45×1010N/m2，其余桥梁参数如表4所示。

表4 各类桥梁具体参数值Table 4 Specific parameter values of various bridges

对于跨座式单轨，其车桥质量比达到1.59，远远大于同等跨度的其他4种交通形式的桥梁，频率改变也更明显，最大变化率接近40%，如表5所示；双线地铁与高速铁路桥梁的最大频率变化仅有20%；高速公路桥梁的频率变化最小，只有15%，客货共线铁路则可接近30%。值得指出的是，这4类交通形式桥梁车桥质量比均小于1，即列车质量小于桥梁。

表5 32 m跨长跨座式单轨桥梁一阶有载频率变化Table 5 The first-order on-load frequency variation of a 32 m long straddle monorail bridge

计算结果表明，在列车第一个轴重进桥时频率呈逐渐下降趋势，而列车最后一个轴重出桥阶段，频率又逐渐上升为无载频率，而中间阶段时，频率则呈现出上下波动的趋势，且均在最小有载频率附近波动，因此可认为桥梁结构在车辆通过时有载频率基本不变。

以跨座式单轨列车为例，车桥质量比为1.59时，此时列车质量远大于桥梁质量，给出有载频率计算值随时间变化曲线图，如图9所示。频率变化图成对称分布，且桥梁有载频率在列车过桥中呈稳定的周期性变化，但波动不大，其他4类交通形式桥梁频率变化曲线近似，不再一一列出。

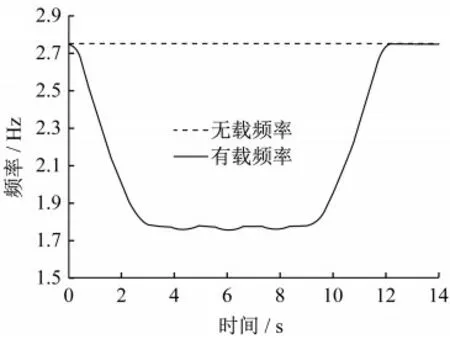
图9 跨座式列车频率随时间变化图Fig.9 Diagram of straddle train frequency change with time

如图10所示，列车频率的变化随车桥质量比的变化呈正相关特征，跨座式单轨列车在1.59的车桥质量比下，频率变化率达到了36%，此类情况应引起工程设计人员注意，以免计算时对桥梁结构实际的动力响应出现较大误差。车桥质量比大于1时，即列车质量大于桥梁质量时，频率变化超过了30%，此时，有载频率与无载频率相差明显，而当车桥质量比小于0.3时，频率变化仅为10%左右，对结构无载频率无较大影响，尤其对于部分重型桥梁，如32 m跨度可以达到900～1 000 t，此时车桥质量比很小，不足0.1，频率变化几乎可以忽略不计，而跨座式单轨则要求设计人员能考虑到桥梁的频率变化，以此进行结构计算。应当特别指出的是，本文在考虑列车荷载时，均将桥梁以最大可能性进行加载，而在实际工程中，这类情况出现概率较低，特别是在双线高速铁路和多车道高速公路中，实际的车辆荷载通常较小，小于设计考虑的加载，而其桥梁质量却比单线式铁路桥梁或双车道高速公路桥梁高出数倍，车桥质量比更小，使得有载频率变化可以忽略不计。

图10 频率随车桥质量比变化曲线Fig.10 Frequency change curve with vehicle-bridge mass ratio

3.2 不同类型交通形式桥梁较高阶有载频率分析

在实际工程中，高阶模态只有在振动初始阶段比较明显，频率阶数越高，因阻尼作用造成的衰减越快，在结构实际的振动中，主要由前几阶模态控制。因此本文在已分析一阶频率的基础上，进一步计算前四阶有载频率的变化及其车桥质量比的影响。计算推导过程同一阶有载频率计算类似，以车桥质量比最大的跨座式单轨和最小的高速公路为例，对桥梁前四阶频率的变化进行分析研究。

计算结果表明，不论是跨座式单轨还是高速公路，随着频率阶数的提高，有载频率在列车通过桥梁时变化波动越来越大，其中一阶有载频率变化最稳定，在列车入桥和出桥阶段逐渐减小或增大，而二、三、四阶有载频率则始终呈现出剧烈的上下波动；但频率阶数对桥梁有载频率的最大变化率影响较小如图11所示。

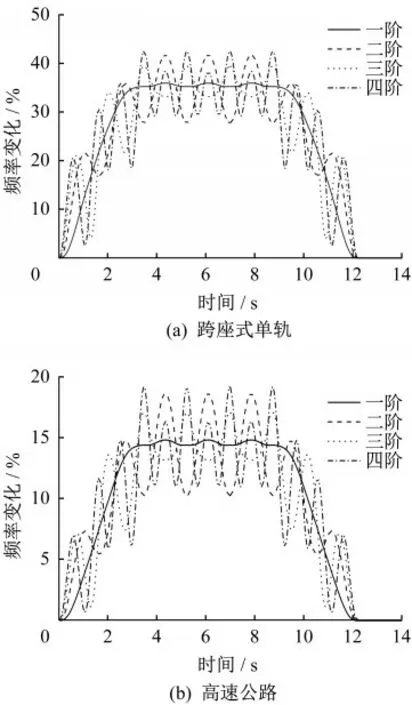
图11 不同桥梁类型前四阶有载频率变化率Fig.11 The first four-order load frequency changes rate of different bridge types

图12表示跨座式轻轨交通和高速公路桥梁有载频率前十阶相对无载频率的变化率，可以看出对于车桥质量比较大的跨座式单轨桥梁其各阶有载频率变化率均在40%左右，而高速公路桥梁，前十阶有载频率变化率均在15%～20%。

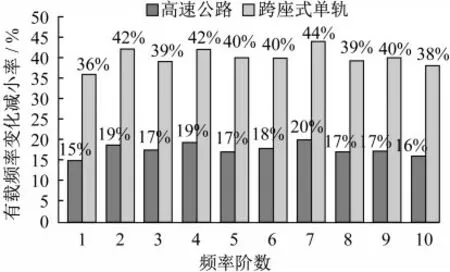
图12 前十阶有载频率减小变化率Fig.12 The first ten orders of load frequency decrease rate of change

4 结论

本文首先分析了不同交通形式下常用中等跨度的桥梁之间的质量比和车辆荷载的质量比，然后计算分析对比了车辆过桥时它们之间的有载频率变化大小和规律，分析结果表明：

（1）跨座式交通桥梁由于车桥质量比远大于其他类型交通形式的桥梁，所以它的有载频率和无载频率变化的幅度较大，减小率可达到36%左右。公路桥梁由于车桥质量比较小，其有载频率相对于无载频率变化幅度较小，可以忽略。

（2）车辆过桥时，梁跨结构有载频率基频量值随时间变化比较平缓稳定，频率阶数越高，其量值随时间变化愈加剧烈，呈随时间上下波动状态。

（3）梁跨结构各阶有载频率与其对应的无载频率，其变化率均比较接近，即车辆过桥时桥梁各阶有载频率均以基本相同的变化率发生改变。

结构的自振特性是影响结构动力响应的重要因素。对于跨座式轨道交通桥梁结构而言，要重视其车桥质量比变化对结构有载频率的影响作用，尤其在制定设计规范的动力参数限值时，不宜简单引用其他轨道交通桥梁规范相应的条文，必须做一些必要的研究分析工作。随着今后城市轨道交通建设的发展、高强材料的应用和城市景观的要求，城市轨道桥梁将向着纤细苗条方向发展，车桥质量比会进一步增大，桥梁有载频率变化也更加明显，应当注重考虑频率变化带来的桥梁动力性能改变，这也是当前轨道桥梁设计和规范制定中需要注意的一个问题。